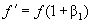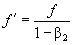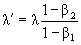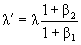Естествознание: Курс лекций

О.Е. Акимов

Лекция 4. Эффект Доплера

Вопросы эффекта Доплера рассматриваются также на следующих страницах:

• Введение в акустику. Природа звука и ультразвука
• Введение в конструктивную физику
• О формуле, описывающей классический эффект Доплера
• Ошибочность релятивистской формулы Доплера
• Квантовая теория Доплер-эффекта
• Эксперимент Майкельсона – Морли
• Лекция 4. Эффект Доплера
• Часто задаваемые вопросы по эффекту Доплера
• Идиотский расчет эффекта Доплера
• Использование в медицине поперечного эффекта Доплера для ультразвуковой диагностики сердечно-сосудистой системы
• Эффект сдвига воспринимаемой длины волны в красную область
• Моделирование волновых процессов. Эффект Доплера

Пражский профессор Христиан Доплер (1803 – 1853) в 1842 г. опубликовал статью «Об окрашенном свете двойных звезд и некоторых других небесных светил», где впервые рассмотрел вопрос об изменении частоты излучения света в зависимости от движения его источника или приемника. Предсказанный им эффект относится к колебаниям любой природы, так что его механизм действия можно проиллюстрировать на примере расходящихся кругов по поверхности воды от периодически погружаемого в воду поплавка i. Если поплавок i покоится, то на водной глади образуется ряд вложенных колец различного диаметра, имеющих общий центр (рис. 4.1а); если поплавок i равномерно и прямолинейно перемещается, продолжая совершать колебания, то центры окружностей сместятся вдоль оси x (рис. 4.1б).

Рис. 4.1. Эффект Доплера: источник колебаний i покоится, приемник A движется со скоростью v₁ по направлению к источнику (а); приемник A покоится, источник i движется со скоростью v₂ по направлению к приемнику (б). В обоих случаях будет наблюдаться изменение длины волны λ.

Обозначим параметры собственных колебаний поплавка следующими буквами: f – частота колебаний, T – период, λ – длина волны, а через c – скорость распространения волны по поверхности воды. Тогда для неподвижного источника и покоящегося наблюдателя будут справедливы следующие соотношения: λ = cT, λ = c/f, T = 1/f.

Теперь вообразите, что поплавок i никуда не перемещается, а вы в роли наблюдателя (или приемника A) плывете на лодке со скоростью v₁ < c вдоль оси x по направлению к источнику колебаний i (рис. 4.1а). Понятно, что длина волны λ для вас уменьшится и станет равной λ₁. Так как вы плывете навстречу волне, набегающей на вас, то относительная скорость окажется равной сумме скоростей: c + v₁. Очевидно, что длина волны λ₁ во столько раз меньше длины волны λ, во сколько раз c меньше c + v₁, т.е.

,     ,     .

Период колебаний T для вас также сократится и будет равным T₁, а частота f, напротив, увеличится и станет равной f₁:

,     ,     .

Если лодка останется неподвижной относительно водной поверхности, а источник колебаний i начнет перемещаться со скоростью v₂ < c по направлению к приемнику A, как указано на рис. 4.1б, то воспринимаемая длина волны λ₂ также уменьшится, но уже в иной пропорции. Так как поплавок движется в ту же самую сторону, что и волновой фронт, их относительная скорость будет равна разности двух скоростей: c – v₂. Длина λ₂ во столько раз меньше длины λ во сколько раз c – v₂ меньше c; аналогично в отношении периода T₂ и частоты f₂:

,     ,     ,     ,     .

Важно подчеркнуть, что сокращение длины волны и периода колебаний при движущемся наблюдателе и покоящемся источнике происходит за счет сложения скоростей c + v₁, а при движущемся источнике и покоящемся наблюдателе это сокращение происходит уже по другому закону – за счет вычитания скоростей: c – v₂. Таким образом, благодаря эффекту Доплера принцип относительности движения источника и приемника волн нарушается: по измеренным параметрам волнового процесса всегда можно определить, что относительно чего движется – либо источник движется относительно приемника, либо приемник движется относительно источника, другими словами, движение источника и приемника носит абсолютный характер.

Если в рассмотренных двух случаях направления скоростей v₁ и v₂ изменить на противоположные, то в обоих случаях будет наблюдаться увеличение длины волны и периода колебаний, которое будет происходить тоже по различным законам. В табл. 4.1, помимо четырех типов раздельного движения источника и приемника колебаний, указаны еще четыре случая их совместного перемещения. Две последние формулы свидетельствуют, что когда источник и приемник колебаний движутся в одном направлении с одинаковой скоростью, приемник будет регистрировать ту же самую длину волны, период и частоту колебаний, что и при неподвижном источнике и приемнике. Следовательно, такие приборы, как интерферометр Майкельсона, в котором источник света и приемник (в качестве приемника могут выступать зеркала и экран детектора, где возникают интерференционные полосы) перемещаются совместно, не пригодны для регистрации своего движения относительно светоносной среды (если предположить, что таковая имеется); все волновые процессы, включая интерференционную картину, в таких приборах будут происходить так, как будто бы прибор неподвижен.

Таблица 4.1

Состояния приемника A и источника i	Принимаемая длина волны λ'	Принимаемая частота f '
A и i сближаются: A движется, i покоится
A и i сближаются: A покоится, i движется
A и i удаляются: A движется, i покоится
A и i удаляются: A покоится, i движется
A и i оба движутся навстречу друг ругу на сближение
A и i оба движутся в противоположные стороны на удаление
A и i оба движутся в положительном направлении оси x
A и i оба движутся в отрицательном направлении оси x

Формулы, вошедшие в табл. 4.1, были получены Доплером, но все они носят частный характер, так как справедливы только для случая, когда приемник A и источник i находятся на оси x и их векторы скорости v₁ и v₂ направлены строго по горизонтали. Каков же будет вид формулы, описывающей доплер-эффект, для любых направлений векторов скорости?

Авторство нижеследующих формул:

,     .

вошедших во все современные справочники и учебники, приписывается Лоренцу. Он посчитал, что если к относительным скоростям β₁ и β₂ приписать по соответствующему косинусу cosθ₁ и cosθ₂, то тем самым будет учтена всевозможная направленность векторов v₁ и v₂, Лоренц думал, наверное, что на изменение длины волны λ' и частоты колебаний f ' может оказывать влияние лишь проекции скоростей v₁ и v₂ на вектор c, т.е. величины v_пр1 и v_пр2 (рис. 4.2а), а не сами векторные разности: c – v₁ и c – v₂.

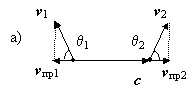
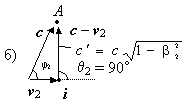
Рис. 4.2. Традиционно эффект Доплера объясняется за счет сложения вектора скорости распространения волны (c) с проекциями скоростей источника v_пр1 и приемника v_пр2 (а). Реально же необходимо производить действия не с проекциями скоростей, а с самими векторами v₁ и v₂. В частности, при движении только источника i изменение длины волны в направлении наблюдателя A произойдет пропорционально разности скоростей c – v₂; формула же c – v_пр2 была бы здесь ошибочной. Поэтому, если угол наблюдения равен θ₂ = ± 90°, то наблюдатель A зафиксирует поперечный эффект Доплера, т.е. зарегистрирует уменьшение длины волны ( λ' < λ ), пропорциональное разности скорости распространения колебаний c и скорости источника v₂ (б).

У Лоренца выходило так, что если покоящийся наблюдатель A смотрит на движущийся источник i под прямым углом ( θ₂ = ± 90° ), то он не обнаружит никакого изменения длины волны λ' и частоты колебаний f ' :

,      .

Такая логика, однако, справедлива для абсолютно плоских волн. Если источник колебаний точечный, волны расходятся в пространстве сферическим образом или кругами в двумерном случае. Источники ограниченных размеров будут излучать искривленные волны, существенно отличающиеся от плоских волн. Всякое искривление линии волнового фронта повлечет за собой поперечный эффект Доплера. Это наиважнейшее утверждение находит подтверждение на практике (см. Использование в медицине поперечного эффекта Доплера для ультразвуковой диагностики сердечно-сосудистой системы ).

Для перемещающегося точечного источника (4.1б) можно вычертить векторную диаграмму, представленную на рис. 4.2б. Пунктирная линия демонстрирует, что при угле наблюдения θ₂ = ± 90° поперечный эффект Доплера очевидным образом дает о себе знать, так как λ' < λ. Элементарная логика рассуждений или непосредственное измерение по чертежу дают единственно верные значения воспринимаемой длины волны λ' и частоты колебаний f ' :

,      .

Если «классическая» физика отрицает так называемый поперечный доплер-эффект при θ₂ = ± 90°, то релятивистская физика, напротив, признает его, причем факт увеличения принимаемой частоты колебаний f ' по сравнению с f сторонниками СТО трактуется как результат «замедления» времени τ:

Эйнштейн в работе [1] прямо указывает на этот «релятивистский эффект», который, по его мнению, может служить экспериментальным подтверждением теории относительности. Таким образом, неучтенный классической физикой поперечный доплер-эффект начал «работать» на неклассическую физику. Читатель сам может убедиться, что обсуждаемый природный феномен имеет вполне «классическое» происхождение. Против того, что круги на воде будут расходиться так, как это показано на рис. 4.1б, видимо, никто возражать не станет. Тогда какие основания имеются у релятивистов, чтобы распространению электромагнитных волн приписывать иную природу? Ровным счетом никаких!

Релятивисты говорят, что электромагнитные колебания имеют особую природу, в частности, они указывают на поперечный характер колебаний. На это необходимо отвечать так: волны на поверхности воды тоже носят поперечный характер, однако их распространение ничем особенным не отличается от продольных акустических волн. И, вообще, с точки зрения геометрии нет никакой разницы между законами распространения акустических и электромагнитных колебаний. Явления интерференции и дифракции для них одни и те же.

Ударная волна существует для звука и света (в последнем случае в виде эффекта Вавилова – Черенкова). Следовательно, формула, описывающая эффект Доплера, также должна выглядеть одинаково для звука и света. Поэтому так называемый поперечный эффект Доплера должен наблюдаться не только для света, но и для звука. Но вот Лоренц еще в конце XIX века при выводе формулы Доплера допустил неоправданное приближение. С тех пор релятивисты и прочие формалисты-феноменалисты, которых особенно много в среде философов и философствующих физиков, в течение века спорят вокруг якобы различной природе звука и света. Суррогатная формула Лоренца стала отправным пунктом теории относительности, но об этом после.

Однако всем формалистам-феноменалистам, лишенным воображения, настоятельно рекомендуется с помощью циркуля и линейки вычертить рисунок с движущимся источником. Если они возьмут λ = 30 мм и β₂ = 2/3, то при θ₂ = ± 90° получат λ' = 22,4 мм, что как раз и соответствует уменьшению исходной длины волны λ в раз. Случай, когда λ' = λ, возможен, но он произойдет при другом угле наблюдения: θ₂ = ± 110°.

Так что же получается, «классические» формулы –

,     .

– ошибочны? Все существующие учебники и книги, где рассказывается о простейшем явление, которое было открыто полторы сотни лет назад, безбожно нас обманывают?

Да, дорогой читатель, к сожалению, это так. Полтора века нехорошие люди, пришедшие в большую и добрую науку, издевались над ней. Они придумали «сокращение» пространства и «замедление» времени; на самом же деле все эти искажения происходили с их мозгами. Когда одни не очень умные люди фантазировали с пространством и временем, другие до небес прославляли их. Не верьте этим взбалмошным ученым, когда они начнут вам морочить голову о якобы особой природе света. Эти изворотливые лгунишки хотят продлить себе счастливое существование на Олимпе науки до бесконечности, для чего пойдут на самые низкие поступки. Многим тысячам настоящих ученых они уже исковеркали жизнь и, поверьте, еще не одна сотня людей по всему миру погибнет от их рук.

Если кто-то думает, что во всем виноват Эйнштейн или какая-то небольшая группа экзальтированных людей, то он сильно заблуждается. Мы имеем дело с огромным социально-психологическим комплексом. Поэтому наша задача состоит не в том, чтобы указать правильную формулу для доплер-эффекта, – хотя это, конечно, важно, – и даже не в том, чтобы раскритиковать с конструктивных позиций формально-феноменалистскую теорию относительности, – чем мы, безусловно, займемся, – главная наша цель более масштабная, и заключается она в том, чтобы вскрыть глубинные социально-психологические механизмы, повинные в этих ужасных для естествознания бедах. В последующих работах мы попытаемся рассказать нашим читателям, как функционирует реальная наука, в которой отсутствуют элементарные средства защиты от самых грубых ошибок, а пока в этом и последующем разделах продолжим анализ эффекта Доплера и все, что с ним непосредственно связано.

*
*   *

Итак, частные формулы, представленные табл. 4.1, справедливы; сейчас ставится задача по получению общих формул для длины волны λ' и частоты колебаний f '. Как и раньше, данную задачу разобьем на две подзадачи, рассматривающие отдельно движение наблюдателя A при покоящемся источнике i (рис. 4.3а), и движение источника i при покоящемся наблюдателе A (рис. 4.3б). На рис. 4.3а вычерчен треугольник 0AA', в котором сторону λ выразим через две другие стороны λ' и β₁λ', а также через прилегающие к λ косинусы углов π – θ₁ и θ₁ – φ₁, получим:

λ = λ'cos (θ₁ – φ₁) + β₁λ'cos (π – θ₁) или

.

Из рис. 4.3б треугольник 0iA аналогичным образом находим формулу для измененной длины волны λ' для случая движения источника i при покоящемся наблюдателе A:

λ' = λcos (θ₂ – φ₂) + β₂λcos(π – θ₂) или λ' = λ[cos (θ₂ – φ₂) – β₂cos θ₂].

Рис. 4.3. Геометрическая схема расположения источника i приемник A и волнового фронта, отвечающего длине волны λ. Имеем два случая: источник колебаний i покоится в точке 0, приемник A движется с относительной скоростью β₁ по направлению к точке A' (а); приемник A покоится, источник i движется по горизонтали с относительной скоростью β₂ (б).

Обратите внимание, в чем главное отличие последней формулы от традиционно принятой в физике:

λ' = λ(1 – β₂cos θ₂).

В принятой формуле вместо cos (θ₂ – φ₂) стоит единица; косинус обратится в единицу при равенстве углов: θ₂ = φ₂. Именно такого рода приближение делают авторы при выводе традиционной формулы. Им кажется, что принятые формулы верны, если точку наблюдения, A расположить вдали от источника i (рис. 4.3б), т.е. когда выполняется условие iA << λ. О точной формуле, когда длина волны и расстояние от источника до приемника сопоставимы, они не думают.

Чтобы разубедиться в ошибочном мнении, взгляните еще раз на рис. 4.1б и представьте себе, что вместо полных четырех волн у вас между каждыми двумя соседними кольцами расположено миллион новых колец, что будет отвечать уменьшению первоначальной длины λ в 10⁶ раз. Разве от этого поперечный эффект Доплера исчезнет? Нет, конечно! Если раньше ваша волна имела длину λ = 30 мм и поперечная длина волны равнялась λ' = 22,4 мм, то теперь у вас будет λ = 30 · 10 ^–6 мм, а длина, наблюдаемая перпендикулярно направлению движения источника также уменьшится в миллион раз: λ' = 22,4 · 10 ^–6 мм.

Следовательно, дело вовсе не в том, на каком расстоянии от источника колебаний находится наблюдатель, все зависит от величины скорости движения источника v₂ относительно скорости распространения волн в среде c. Если выполняется условие v₂ << c, то θ₂ = φ₂ и вы еще можете пользоваться традиционной формулой, но если указанное условие не выполняется, то традиционная формула дает огромную погрешность. Она вообще не применима для случая, когда источник колебаний движется выше скорости распространения этих колебаний, т.е. когда возникает ударная волна. Между тем точная формула дает угол при вершине конуса ударной волны. Нижеследующие рассуждения подтвердят это.

Действительно, углом наблюдения у нас является θ₂; именно он выступает в роли свободного параметра для формулы Доплера, которая представляет собой уравнение окружности в полярных координатах, центр которой совмещен с движущимся источником. Традиционная формула Доплера для движущегося источника и покоящегося приемника дает кривую, которая в математике называется кардиоидой. От угла φ₂, образованного волновым вектором и вектором движения источника, необходимо избавиться. Но прежде чем к этому приступить, сделаем еще одно важное замечание.

В дискуссиях на эту тему релятивисты часто говорят, что истинным углом наблюдения является угол φ₂, а не θ₂. При этом они ссылаются на тот аргумент, будто волновой фронт должен быть расположен к наблюдателю A непременно под прямым углом (нормально). При этом они ссылаются на определение длины волны, которое, однако, справедливо только для случая покоящегося источника. Формалисты не могут понять, что волновой фронт может подходить к приемнику под любым углом.

Представьте себе поплавок на поверхности воды. Мимо проплывает лодка, от которой расходятся волны. Поплавок начинает колебаться под воздействием этих волн. Частоту или период колебаний поплавка мы можем воочию наблюдать и замерить, хотя из-за непрерывного движения лодки волны к поплавку подходят с различной стороны. По чертежам (рис. 4.1б и 4.3б) можно легко установить, что на линии 0A определение длинны волны как раз и не работает; неизменная длина волны появляется только на линии iA, что и говорит нам о том, что углом наблюдения является θ₂, а не φ₂.

Более того, наблюдатель или приемник A здесь в общем-то ни при чём. Вывод уточненной формулы Доплера можно произвести и без них. Для этого нужно всю совокупность сдвинутых концентрических колец на поверхности воды (рис.4.1а) сфотографировать из положения, когда наблюдатель находится не в плоскости распространения волн (оси x и y), а над плоскостью со стороны оси z. Затем непосредственно на фотографию нанести прямоугольную сетку декартовых координат и выразить все окружности уравнениями аналитической геометрии. В декартовых координатах мы получим систему уравнений второго порядка, отвечающих системе окружностей.

Далее, эту систему уравнений необходимо переписать для полярных координат, в которых обычно представляется формула доплер-эффекта. В этом случае мы получим систему уравнений точных формул Доплера с равномерно возрастающим радиус-вектором. Такой вывод окажется более трудоемким, зато исходная картинка будет взята, что называется, непосредственно из физического эксперимента, когда длина волны может быть измерена линейкой. Здесь уже некуда будет «воткнуть» пресловутого наблюдателя, так как уравнения окружностей справедливы для любого угла наблюдения.

Чтобы избавиться от угла φ₂, воспользуемся теоремой синусов. Для треугольника 0iA (рис. 4.3б) она запишется следующим образом:

.

Отсюда имеем

sin (θ₂ – φ₂) = β₂sin θ₂.

Уточненная формула

λ' = λ[cos (θ₂ – φ₂) – β₂cos θ₂]

приобретет вид:

.

Таким образом, cos (θ₂ – φ₂) зависит от выражения, куда входит относительная скорость β₂: чем меньше β₂, тем ближе cos (θ₂ – φ₂) к единице.

Однако уточненную формулу для доплер-эффекта полезно выразить и через угол φ₂, поскольку такая форма вскрывает векторную сущность формулы. В самом деле, из треугольника 0iA (рис. 4.3б) по теореме косинусов имеем:

.

или окончательно:

.

Это простое выражение отражают известный математический факт – сложение двух векторов, неважно какой природы. Если речь идет об эффекте Доплера, значит складывать нужно скорость распространения колебаний в среде и скорость движения источника этих колебаний. Можно спорить, что является углом наблюдения – θ₂ или φ₂, – но отрицать саму формулу сложения двух векторов невозможно. Почему вместо данной формулы, которая была известна еще до открытия эффекта Доплера, исторически утвердилась суррогатная формула Лоренца – это другой вопрос, который мы затрагивать пока не станем.

Теперь обобщим результаты. Раздельно полученные формулы для случая одновременного движения наблюдателя A и источника i естественным образом объединяются в одну формулу. С точки зрения физики процесса, удобно ввести три частоты колебаний: f – собственная частота колебаний источника, f_ср – частота колебаний среды и f ' – частота, воспринимаемая приемником. Тогда будем иметь:

f ' = f_ср [cos (θ₁ – φ₁) – β₁cos θ₁]  и .

Особо подчеркнем, что частота колебаний среды f_ср для всякого эффекта Доплера – касается ли это колебаний воды, воздуха или эфира, – является принципиальной. Без наличия среды никакого волнового процесса не происходило бы вообще. Подстановка второй формулы в первую позволяет связать обе формулы в одну, в которой частота колебаний среды уже не участвует; аналогичное объединение справедливо и в отношении длины волны:

,     .

Этим двум формулам можно поставить в соответствие еще два абсолютно эквивалентных представления:

,     ;

,     ;

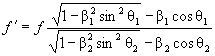Теперь переходим к кульминационному моменту нашего повествования. Сейчас мы покажем, что формулы Доплера для сферически расходящихся волн с высокой точностью совпадает с релятивистскими формулами. В самом деле, из математики известны следующие приближенные выражения:

,     ,     .

Применяя их соответствующим образом к правым и левым частям нижевыписанных приближенных равенств, можно убедиться в их справедливости:

;

;

При углах θ₁ = θ₂ = 0 ошибка максимальна, при углах θ₁ = θ₂ = π/2 оба приближенных равенства превращаются в тождества. Между тем как раз последний вариант релятивисты воспроизводят в своих экспериментах, пытаясь доказать наличие поперечного доплер-эффекта. На самом же деле они подтверждают справедливость точной классической формулы. У нас же появляются неограниченные возможности интерпретировать релятивистские эффекты как исключительно эффекты классической физики.

*
*   *

В 1988 г. группа физиков-экспериментаторов поставила перед собой цель проверить релятивистскую формулу для эффекта Доплера, которая, как известно, дает асимметрию в смещении частот излучения, например ионов водорода (), в «красную» или «фиолетовую» области при смене угла наблюдения пучков ионов с θ₂ = 0 на θ₂ = π. Традиционная формула такой асимметрии не дает, но для уточненной формулы асимметрия получается примерно такой же величины, что и рассчитанная по релятивистской формуле.

Все экспериментальные (λ_экс.) значения, полученные упомянутой группой экспериментаторов, а также данные, рассчитанные по уточненной (λ_класс.) и релятивистской (λ_релят.) формулам, занесены в табл. 4.2. Читатель сам может убедиться в высокой степени совпадения релятивистских и классических величин (λ_класс. = λ_релят.) для этого эксперимента, результаты которого опубликованы в [2].

Таблица 4.2

E, кэВ.	β · 10 –2	cos θ	λк. экс.	λк. класс.	λк. релят.	λф. экс.	λф. класс.	λф. релят.
150	1,264	0,204	1,72	1,74	1,74	1,68	1,64	1,64
175	1,366	0,210	1,91	1,94	1,94	1,86	1,83	1,83
180	1,385	0,202	1,87	1,89	1,89	1,81	1,78	1,78
200	1,460	0,201	1,97	1,99	1,99	1,90	1,86	1,86
210	1,496	0,204	2,05	2,07	2,07	1,96	1,94	1,94
225	1,549	0,206	2,11	2,17	2,17	2,05	2,02	2,02
250	1,632	0,198	2,16	2,20	2,20	2,09	2,04	2,04
260	1,665	0,206	2,30	2,33	2,33	2,20	2,17	2,17
275	1,712	0,207	2,37	2,41	2,41	2,28	2,24	2,24
300	1,788	0,200	2,40	2,44	2,44	2,29	2,25	2,25
1500	4,000	0,222	6,24	6,30	6,30	5,40	5,35	5,35
1750	4,315	0,222	6,87	6,84	6,84	5,75	5,73	5,73
2000	4,618	0,219	7,34	7,27	7,27	5,95	6,00	6,00

Тех, кого интересуют детали эксперимента, мы отсылаем непосредственно к публикации, остальным сообщаем, что ионы водорода разгонялись на ускорителях НГ – 400 (до 300 кэВ) и ЭГ – 5 (до 2000 кэВ), установленные в Радиевом институте им. В.Г. Хлопина. Токи пучка ионов составили приблизительно 50 мкА для энергий 150 – 300 кэВ и 10 – 12 мкА для энергий 1500 – 2000 кэВ. Углы наблюдения равнялись примерно 77° и 257°. Несмещенная линия водорода отвечает длине волны λ = 656,28 нм; экспериментальные и рассчитанные смещения этой линии в красную (т.е. в область более длинных волн) и фиолетовую (т.е. в область более коротких волн) приведены в табл. 4.2 в единицах нм. Главное, что демонстрирует приведенная таблица, так это хорошее совпадение значений смещений, рассчитанных по уточненной формуле классической физики:

,

со значениями смещений, рассчитанных по релятивистской формуле:

.

Совпадение расчетных значений с экспериментальными данными для диапазона энергий 150 – 300 кэВ неудовлетворительное, а для 1500 – 2000 кэВ вполне приемлемое. Такая оценка эксперимента основывается на анализе табл. 4.2, который проводился по следующей методике. Средняя разность между красными и фиолетовыми экспериментальными смещениями –

Δλ_экс. = λ_{к. экс.} – λ_{ф. экс.} ,

для энергий 150 – 300 кэВ составила 0,07 нм, для энергий 1500 – 2000 кэВ – 1,12 нм. Средняя разность между красными и фиолетовыми рассчитанными смещениями –

Δλ_расч. = λ_{к. расч.} – λ_{ф. расч.} ,

для энергий 150 – 300 кэВ составила 0,14 нм, для энергий 1500 – 2000 кэВ – 1,11 нм. Таким образом, погрешность эксперимента δ –

при 150 – 300 кэВ составила 43%, а при 1500 – 2000 кэВ – менее 1%, что вполне объяснимо. В диапазоне энергий 150 – 300 кэВ средняя разность между экспериментальным и рассчитанным значениями по красному и фиолетовому смещениям (Δλ = λ_экс.– λ_расч.) составила примерно 0,03 нм, что как раз и составляет погрешность δ' в 43% –

для энергий 1500 – 2000 кэВ разность Δλ, по-прежнему, равна примерно 0,03 нм, а Δλ_экс.  составляет 1,12 нм, так что погрешность δ ' будет равна около 2,5 % (δ' ≠ δ). Погрешность δ' объясняет погрешность δ и наоборот; сравнение расчетных данных с экспериментальными можно производить как по величине δ', так и по δ. В итоге, опытная серия измерений, проведенная на ускорителе ЭГ – 5, работающем в диапазоне энергий 1500 – 2000 кэВ, одинаково подтверждает теоретические ожидания как сторонников классической физики, так и сторонников релятивистской физики; эксперимент, проведенный на ускорителе НГ – 400, работающем в диапазоне энергий 150 – 300 кэВ, можно сказать не удался, так как величина рассогласования между экспериментом и расчетом слишком мала по сравнению с самой величиной смещения.

Однако иной вывод сделали авторы указанной статьи. Сразу в аннотации к статье они отметили «систематическое расхождение между экспериментальными и расчетно-теоретическими данными» во всём диапазоне энергий, причем для энергий 1500 – 2000 кэВ по их расчетам погрешность δ в среднем составила 54 %. Не будем вдаваться в подробности их методики теоретического расчета, укажем лишь на исходную релятивистскую формулу, справедливость которой они пытались установить –

Именно это выражение фигурировало в статье [2], а не выше написанное выражение для λ_rel. Казалось бы, данная формула для λ' больше отвечает движущемуся приемнику, во всяком случае, она соответствует уточненной классической формуле для движущегося наблюдателя:

.

Различие в формулах заключается лишь в знаке перед косинусом, что приводит к противоположному эффекту смещения спектральной линии, т.е. когда наблюдение пучка ионов водорода ведется под углом 77° результат смещения линии будет таким, как при наблюдении пучка под углом 257°, и наоборот. В эксперименте же разгонялись ионы водорода , т.е. двигался источник. Неужели экспериментаторы ошиблись с формулой? Именно так и произошло. Однако нужно иметь в виду, что расчетные значения, произведенные по формуле для движущегося приемника, отличаются от расчетных значений, произведенных по формуле для движущегося источника, на малую величину, пропорциональную β², что составляет менее 1 % от приведенных в табл. 4.2 значений λ_релят. и λ_класс..

В книге У.И. Франкфурта и А.М. Френка «Оптика движущихся тел» [10] подробно разбираются эксперименты по проверке оптического эффект Доплера, в том числе знаменитый опыт Айвса – Стилуэлла 1938 г., который, кстати, проводился при очень небольших энергиях – 28 кэВ. На с. 126, где излагается методика проверки, мы обнаруживаем совершенно иную формулу для движущихся источников излучения:

.

Так кто же прав в написании формулы для движущегося источника излучения: Айвс и Стилуэлл или группа экспериментаторов из Радиевого института им. В.Г. Хлопина? Чем больше знакомишься с литературой, тем большая неопределенность возникала в отношении релятивистской формулы, описывающей доплер-эффект. Потом приходишь к выводу: данная неопределенность в формулах носит принципиальный характер и в рамках теории относительности устранена быть не может.

Как уже говорилось, различие в количественных результатах, полученных по формулам для движущегося приемника и движущегося источника, малозаметное, поэтому экспериментальные данные не позволяют обнаружить принципиальное различие в написании формул. Однако сравнение текстов указанных статей говорит о неоднозначности отправных математических выражений. Сейчас мы займемся этим наиболее любопытным из существующих в релятивистской теории парадоксов.

Литература

[1] Эйнштейн А. Собрание научных трудов. Т. 1, – М.: Наука, 1965, с. 49 – 50.
[2] Победоносцев Л.А., Крамаровский Я.М., Паршин П.Ф. и др. Экспериментальное определение доплеровского смещения линий водорода на пучках ионов в диапазоне энергий 150 – 2000 кэВ. Журнал технической физики, т. 59, вып. 3, 1989, с. 84 – 89.
[3] Эйнштейн А. К электродинамики движущихся тел. СНТ, т. 1. – М.: Наука, 1965, с. 26.
[4] Лауэ М. Статьи и речи. – М.: Наука, 1969, с. 230.
[5] Справочник по физике Б.М. Яворского и А.А. Детлафа. – М.: Наука, 1985.
[6] Левич В.Г. Курс теоретической физики, т.1 – М.: Физматгиз, 1962.
[7] Сивухин Д.В.Общем курсе физики, т. IV, «Оптика» –М.: Наука, 1985.
[8] Россель Ж. Общая физика. – М.: Мир, 1964.
[9] Франкфурт У.И. Очерки по истории специальной теории относительности – М.: Издательство АН СССР, 1961.
[10] Франкфурт У.И., Френк А.М. Оптика движущихся тел – М.: Наука, 1972.