Часто задаваемые вопросы по эффекту Доплера

Олег Акимов

Вопросы эффекта Доплера рассматриваются также на следующих страницах:

Мне казалось, что данная тема в этих файлах изложена исчерпывающим образом. Ведь достаточно набрать элементарную программу для MATLAB-пакета, чтобы построить волновой фронт, рассчитанный по ошибочной старой (1) и точной новой (2) формулам. Вот эта программа:

r = 1; b = 3/4; j=1;
for t = 0 : 0.01 : 6.28
s(j) = t;
s1(j) = b*sin(s(j));
s2(j) = (s1(j))*(s1(j));
c(j) = cos(s(j));
% формула (1):
r1(j) = r*(1 - b*c(j));
% формула (2):
r2(j) = r*(sqrt(1 - s2(j)) - b*c(j));
j = j + 1;
end
h1 = polar(s,r1);
%h1 = polar(s,r2);
set(h1);

Меняя относительную скорость движения источника (параметр b = 1/2, 3/4, 1, 2, 3, ...), можно проследить, как меняется форма волнового фронта. Формула (2) дает правильные окружности при любом значении параметра b, а формула (1) при b > 1 дает загогулины.

Тем не менее, школьники, студенты и преподаватели продолжают присылать мне письма, в которых просят разъяснить непонятные им места. Ниже приводится моя переписка с неким Ивановым, который задавал вопросы, возражал или делал замечания по теме эффекта Доплера. Надеюсь, что мои комментарии помогут лучше усвоить данную тему.

1-е замечание Иванова

Цитата: «Если источник звуковых или световых волн покоится относительно однородной среды, где распространяются колебания, ...» [1, абзац 1 ]

Важная особенность движения волн в среде — необходимость существования этой среды. При отсутствии среды волнам нет в чём [?] распространяться. Механизм образования и движения волн частиц в среде частиц совсем иной [?], чем в пространстве без среды. Поэтому формулы распространения волн в среде в общем случае не подходят для описания волн в вакууме. Например, звуковые волны в вакууме не распространяются, и формулы для них, выполняющиеся даже для достаточно малой плотности воздуха, для нулевой плотности воздуха не применимы.

1-й комментарий Акимова

Данное замечание оппонент сделал, целиком находясь на позиции релятивиста. Разве ему не понятно, что по большинству вопросов физик-релятивист принципиально расходится с физиком-классиком. Так к чему нам обыкновенная констатация своих позиций? Для моего оппонента правильнее было бы искать противоречия в рамках внутренней логики автора. А так получается, что автор должен в ответ на замечание оппонента просто обозначить свою позицию. Так вот, с точки зрения классической физики, которой придерживается автор, волны любой природы распространяются только в среде.

Почему? Да хотя бы потому, что невозможно объяснить такое широко распространенное явление, как интерференция. Оптические волны интерферируют, следовательно, свет распространяется тоже в среде (ее часто называют эфиром). Без среды нельзя объяснить и эффект Доплера, о котором речь пойдет впереди. Релятивисты так напутали с формулами, что на сегодняшний день существует несколько противоречащих друг другу математических выражений. Подробно об этом поговорим позже, но уже сейчас заметим: формулы, описывающие распространение световых возбуждений в эфире, в точности совпадают с формулами для звуковых возбуждений, распространяющихся, например, в воздухе.

Спросите: почему релятивисты отрицают мировую среду для света? Отвечаю: они — формалисты, их не интересует конкретные механизмы, моделирующие физические процессы, в том числе, явление интерференции и эффект Доплера. В частности, они не знают и знать не хотят, почему в одном месте пространства появляются светлые пятна, в другом — темные. Другими словами, они — не физики. Вместо физического осмысления той или иной ситуации, релятивисты предпочитают заниматься математическими спекуляциями, с помощью которых они пытаются подогнать новые эмпирические данные под свои догматические формулы вековой давности.

2-е замечание Иванова

Цитата: «...длина волны λ (λ — расстояние межу двумя одинаковыми фазами колебаний)...» [ 1, абзац 1 ]

Это просто неверное определение. Общепринятой формулировкой определения этого термина является: "Длина волны — характеристика синусоидальной (гармонической) волны, равная расстоянию между двумя ближайшими точками среды, разность фаз волны в которых равна 2π". [Словарь по естественным наукам].

Таким образом, длина волны измеряется только в направлении распространения волны, так как расстояние между двумя произвольными точками любых синфазных поверхностей волны — величина неопределенная, в том смысле, что это расстояние зависит от разности номеров поверхностей, расстояния до источника и, естественно, координат этих точек. Но рассмотрение таких параметров в статье отсутствует. Следовательно, данным определением Вы вводите в заблуждение читателей.

Вы в своей точной формуле рассматриваете сферическую волну радиуса R. Сфера образовывается именно точками волны в одинаковой фазе. По Вашему определению получается, что длина волны может иметь размеры от 0 до 2R, так как для измерения можно выбирать любую пару точек на этой сфере. А если рассмотреть другие сферы вокруг источника, образованные в той же фазе точками волны других периодов, то получится еще большая неопределенность в измерении длины волны.

2-й комментарий Акимова

Во-первых, из приведенного определения непосредственно не следует, что «длина волны измеряется только в направлении распространения волны». Всё, ниже сказанное после этих слов, является произвольным домысливанием моего оппонента.

Во-вторых, приведенное определение сильно заужено. Почему говорится только о гармонических колебаниях строго синусоидального вида? Синусоида предполагает равномерное вращение по кругу некой математической точки, а что если ее вращение происходит по эллипсу или по более сложной замкнутой кривой? Тогда, очевидно, колебания уже нельзя назвать гармоническими. Но главное, в определении ничего не сказано о состоянии источника — находится ли он в покое или в движении. Что считать длиной волны, когда скорость источника превысит скорость распространения волны и возникнут ударные волны? Если источник колебаний движется со скоростью меньше скорости распространения возбуждений среды, а именно такая ситуация рассматривается в начале статьи [ 1 ], то приведенное определение уже недостаточно.

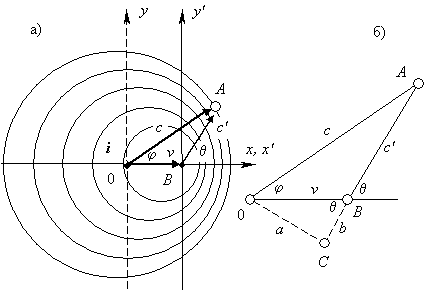Рис. 1. Чертеж (а) представляет собой застывшее изображение процесса распространения волн при движущемся источнике колебаний ( i ). Пока волновой фронт, испущенный из точки 0, дойдет до точки А, источник колебаний i окажется в точке В. Чтобы найти выражения для векторной суммы векторов v и c, на чертеже (б) показан вспомогательный прямоугольный треугольник.

На рис. 1 (он взят из [ 1 ]) имеется два направления — 0А и ВА. Оппонент думает, как я предполагаю, что длина волны определяется вдоль направления 0А, где в конечной точке А волновой вектор направлен строго перпендикулярно к касательной волнового фронта. Однако на этом направлении между гребнями разные расстояния, т.е. длина волны здесь не определена. Между какими двумя гребнями считать здесь длину волны? Ведь следующий волновой фронт накатит на точку А, когда ее волновой вектор пройдет максимум и нужно будет брать его проекцию. Где одинаковые расстояния между гребнями? Только на отрезке ВА. Значит, углом наблюдения за перемещающимся источником, который в данный конкретный момент окажется в точке В (в точке 0 его давно нет), является угол θ, а не угол φ, т.е. угол между векторами скорости v и c.

В-третьих, мой оппонент – яркий представитель формалистского направления в науке. Он считает, если в словаре, изданном учреждением официальной науки, дается какое-либо определение, то вся последующая наука должна шагать в ногу с автором этого «академического» определения. Оппонент не желает схватить суть физического явления, он будет цепляться к первому непонравившемуся ему слову и изводить автора до тех пор, пока тот не умрет от его схоластики.

Как обыкновенно строится критика теорий? Выбирается что-то главное в ней, с чем не согласен оппонент, называется причина этого несогласия, а затем идет детализация и подкрепление главного аргумента оппонента более мелкими доводами типа неточности определения длины волны и т.д.

Ведь очевидно, что автор не собирался приводить здесь какие-то ГОСТы на определения длины волны, периода колебаний и частоты. Он просто ввел самые общие представления о λ, T и f для ориентации читателя во всем последующем материале, чтобы, в частности, написать формулу (1) и обсудить ее справедливость. Если оппонент добивается от автора признания: «Согласитесь, ваше определение не отвечает ГОСТам», то я, автор, согласен: «Да, свое определение я дал мимоходом и, разумеется, не сверял его с принятыми в официальной науке ГОСТами».

Тем не менее, в свете вышеуказанных недостатков официально принятого определения длины волны, не применимости его к рис. 1, я бы ничего не менял в своем более чем скромном определении λ. Единственное, что можно было бы вставить в сказанную мною фразу, так это слово «ближайшие». Термин одинаковые фазы, в общем, подразумевает полный цикл в 2π, но, пожалуй, соглашусь с оппонентом, лучше всё-таки сказать «между двумя ближайшими одинаковыми фазами». Такая фраза выглядит неуклюже, но точнее. И последнее, спор об угле наблюдения полностью разрешится, когда станет понятна его связь с формулой Маха (2) и явлением ударной волны. Но об этом поговорим позже.

3-е замечание Иванова

Цитата: «...Но стоит источнику колебаний сообщить движение в каком-то заданном направлении, как тут же длина волны будет меняться в зависимости от величины скорости источника и направления приёма волн...» [1, абзац 1 ].

Термин "Направление приема волн" — еще одна Ваша уловка. Казалось бы, очевидно, что Вы имеете в виду направление распространение волны (ведь длина волны от неподвижного источника у Вас "по всем направлениям будет одной и той же"), но далее оказывается, что нет, Приемник у Вас принимает волны совсем в другом направлении. При этом Вас не смущает, что даже от неподвижного источника принимаемая Приемником в другом направлении волна (по Вашему же определению) будет иметь длину волны, отличающуюся от полученной по стандартному определению, так как расстояние между ближайшими синфазными точками двух последовательных волн будет отличаться от расстояние между синфазными точками волн в другом направлении (под углом к направлению на то положение Источника, откуда пришла измеряемая волна, см. Рис. 2; в работе [ 2 ] это рис. 6).

Рис. 2. Чертеж иллюстрирует тривиальный факт:
при β < 1 и θ = ±90° точная формула
дает поперечный Доплер-эффект.

Однако для меня очевидно, почему Вам понадобились именно такие неправильные определения длины волны и направления приема волн – чтобы аргументировать в дальнейшем Вашу точную формулу, которая предназначена для описания расстояния между гребнями волн не в направлении их распространения, см. тот же Рис.2.

3-й комментарий Акимова

Проблема снова уперлась в определение длины волны. «Словарь по естественным наукам», как я уже сказал, нас не спасет. Источник непрерывно перемещается, точка А неподвижна и находится в непосредственной близости от источника, т.е. точек 0 и В. Близость источника и приемника позволяет исключить спекуляции релятивистов на приближениях, принятых сегодня для вывода традиционной формулы. В этом случае каждая последующая волна накрывает точку А под заметным углом к первоначальному направлению 0А, так что «стандартное определение» длины волны, за которое ухватился мой оппонент, здесь не работает, так как оно предполагает покоящийся источник, когда длина волны «по всем направлениям будет одной и той же».

Средневековые схоласты могли годами рассуждать, существуют ли у одежной щетки молочные железы вместо того, чтобы взять ее в руки и тщательно осмотреть. Мой оппонент предпочитает извергать из себя Монблан слов вместо того, чтобы взять и показать на рис. 1 длину волны, которая ему кажется верной.

Итак, повторюсь: за длину волны я принимаю отрезок, который получается делением расстояния АВ на число гребней; все эти отрезки будут одинаковыми. Если мой оппонент выберет направление 0А, то все отрезки между гребнями окажутся различными. Какой из них выбрать? Тот, что ближе всего к точке А? Так он ничем не лучше любого другого отрезка между гребнями, причем данные отрезки будут противоречить «стандартному определению» длины волны.

Если оппонент откажется выбирать на рис. 1 отрезок, соответствующий длине волны, он не сможет далее вывести формулу Доплера. Истинная формула выводится только из геометрии чертежа. Ошибочность релятивистской формулы как раз и проистекает из чисто формального ее получения, когда релятивистами была проигнорирована геометрия распространения световых волн.

Все остается в силе и для рис. 2, за исключением одного: при угле θ = ±90° точная формула для эффекта Доплера переходит в формулу, которая характеризует уже поперечный Доплер-эффект, имеющий место, как утверждают релятивисты, только в релятивистской трактовке.

Всем формалистам я рекомендую вычертить чертеж для случая, когда источник находится в покое. Пусть радиальное расстояние между соседними окружностями будет равно 30 мм, что соответствует испускаемой источником длине волны. Далее нарисуйте второй чертеж с теми же окружностями, но уже со сдвинутыми по оси x центрами. Пусть сдвиг центров окружностей соответствует величине относительной скорости β = v/c = 2/3. Наконец, по направлению ВА измерьте расстояние между гребнями. Оно будет равно 22,5 мм, что отвечает релятивистской формуле, описывающей поперечный эффект Доплера.

Правда, у релятивистов здесь возникает неоднозначность, так как квадратный корень у них часто появляется в знаменателе. Это является следствием парадокса штриха, который мы сейчас не станем анализировать. Моего оппонента крайне раздражает простота объяснения «релятивистского» явления на основе обычного здравого смысла, который только и действует в классической физике.

В связи с этим я прошу его для рис. 2, как и для рис. 1, указать отрезок, отвечающий длине волны, как он ее понимает. Отказ выполнить эту просьбу означает, что у него нет никакого четкого пространственного представление о длине волны, которая возникает при Доплер-эффекте для различных углов наблюдения, включая угол θ = ±90°.

4-е замечание Иванова

Цитата: «Источник возбуждает неподвижную точку среды, лежащую на горизонтальной линии движения, а дальше возбуждение распространяется во все стороны самостоятельно, не зависимо как от источника, так и приемника возбуждения. Первая возбужденная точка передает импульс напряжения соседним, те, в свою очередь, передают его следующей группе точек и т.д. ... Руководствуясь одним этим геометрическим принципом, вытекающим из обязательного условия существования неподвижной среды — носителя волн, Христиан Гюйгенс в XVII столетии в "Трактате о свете" смог удовлетворительным образом объяснить важнейшие оптические явления...» [ 2 ].

Рис. 3а. Источник возбуждения среды движется слева направо со скоростью меньше скорости распространения возбуждения (v < c). Рис. 3б. Источник возбуждения движется быстрее, чем распространяется возбуждение в среде (v > c). При этом возникает так называемый конус ударной волны

Принцип Гюйгенса не ограничивает образование вторичных источников волн в среде только положением их на горизонтальной оси (от источника волн в среде в направлении его движения). Поэтому ссылка на принцип Гюйгенса не соответствует Вашему объяснению рисунков 3а и 3б. Принцип Гюйгенса здесь вообще ни при чем, поскольку на рис. 3 нет вторичных источников от пришедших в определенную точку волн, а есть только лишь сам источник, перемещаемый в пространстве.

4-й комментарий Акимова

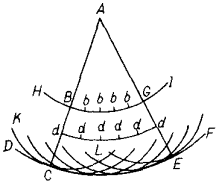
Этим замечанием оппонент сразил автора наповал. Оказывается, он не знаком с действием принципа Гюйгенса и это притом, что автор привел соответствующие картинки (рис. 4) из «Трактата о свете» и в нескольких словах напомнил суть принципа. Теперь давайте обратим внимание на рис. 4б; ниже цитируются слова Гюйгенса, разъясняющие именно эту картинку.

    (a) (б)
(в) (г)

Рис. 4. Чертежи из трактата Гюйгенса, разъясняющие геометрию распространения световых волн.

«По поводу процесса образования этих волн, — пишет Гюйгенс, — следует еще отметить, что каждая частица вещества, в котором распространяется волна, должна сообщать свое движение не только ближайшей частице, лежащей на проведенной от светящейся точки прямой, но необходимо сообщает его также и всем другим частицам, которые касаются ее и препятствуют ее движению. Таким образом, вокруг каждой частицы должна образоваться волна, центром которой она является.

Так, если DCF [рис. 4б] — волна, исходящая из светящейся точки А, ее центра, то частица В, одна из тех, которые находятся в сфере DCF, производит свою отдельную волну KCL, которая коснется волны DCF в С в тот же момент, когда главная волна, исходящая из точки А, достигнет DCF. И ясно, что только точка С волны KCL, т. е. та, которая находится на прямой, проведенной через АВ, коснется волны DCF. Таким же образом остальные частицы, заключенные в сфере DCF, как bb, dd и т. д., создадут каждая свою волну. Но каждая из этих волн может быть только бесконечно слабой сравнительно с волной DCF, образованию которой содействуют все остальные волны той частью своей поверхности, которая наиболее удалена от центра А».

Круговые волны, которые мы видим на рис. 3а и 3б образованы огромным числом «бесконечно слабых», как выразился Гюйгенс, круговых волн, испущенных каждой точкой эфирной среды. Данный принцип исключает появление волновых фронтов в виде кардиоид и эллипсов, как это получается у релятивистов. Этот же принцип действует при образовании ударной волны. В этом случае «бесконечно слабые» волновые фронты складываются в большие круги, которые можно видеть на рис. 3. Затем эти большие круги, несущие суммарную энергию от крохотных кружков, образуют новый фронт — конус ударной волны, в котором уже сосредоточилась энергия от огромного числа больших кругов (или сфер, если говорить о пространстве).

5-е замечание Иванова

Цитата: «На рис. 4 приведены четыре характерных чертежа ... Отсюда проистекает принцип Гюйгенса, дающий единственно верное представление о геометрии волновых процессов, который неизменно подтверждается в опытах со звуком и светом. ...
Таким образом, свет (видимое электромагнитное излучение) вызывается не какими-то специальными частицами материи, а именно колебаниями среды. ...» [ 2 ].

А разве уже доказано, что фотонная теория природы света неверна? Или свет перестал проявлять свойства частиц? Так откуда же следует, что для света остался только "принцип Гюйгенса, дающий единственно верное представление о геометрии волновых процессов", и свет "вызывается не какими-то специальными частицами материи, а именно колебаниями среды"? Таким образом, эти два вывода (утверждения) не верны.

Вполне возможно, что свет является только колебанием среды (эфира), а квантовые свойства света появляются из-за квантованности регистрирующих приборов, и когда-нибудь это будет доказано со всей строгостью, однако на данном этапе мы этого не можем сказать с уверенностью, следовательно, однозначности вывода о наличии только волновых свойств сейчас нет.

5-й комментарий Акимова

В этом замечании, как и в самом перовом, оппонент просто констатирует, что придерживается фотонной теории, а не волновой. Он уже сказал, что для него отсутствует всякая светоносная среда, а значит и волны в ней. Для него есть только пустота, в которой летают световые частицы. С их помощью, однако, нельзя многое объяснить, например, интерференцию и эффект Доплера, о которых уже говорилось. И, наоборот, с помощью волновых представлений можно объяснить квантование энергии возбуждения среды. Одна из первых квантовых теорий была предложена Дж. Дж. Томсоном (см. его статью За пределами электрона ). В этом же направлении много работал и наш соотечественник Александр Саввич Предводителев.

То, что электромагнитная энергия испускается и поглощается порциями, вовсе не вытекает реальность фотонов. По сути дела это понятие вспомогательное, физикам-классикам оно не нужно. Зато из фактов интерференции и эффекта Доплера (сюда можно прибавить дифракцию, аберрацию и многие другие явления) однозначно вытекает справедливость волновых представлений. Понятие квазичастицы по отношению к элементарным частицам работает неплохо, но оно не обладает достаточным конструктивным потенциалом. А вот волновые возбуждения среды могут быть самыми причудливыми; с их помощью можно объяснять квантовые состояния сложных атомных систем.

Так бы я ответил на 5-е замечание, которое, еще раз повторю, носит скорее риторический характер, чем критический. Здесь нет весомых аргументов, на которые можно было бы весомо отвечать. Оппонент не представил автору каких-либо противоречивых моментов в его представлениях. Да и не мог он это сделать, так как вся классическая физика непротиворечива, автор же последовательно придерживается этого мировоззрения. Что же касается теории относительности и квантовой механики, то здесь противоречий предостаточно.

6-е замечание Иванова

Цитата: «Дело усугубляется еще и тем, что люди обычно не делают между ними различий, говоря, что угол φ это и есть угол θ. Такое смешение углов приводит к недоразумению, которое выражается в сохранении старой формулы кардиоиды и отрицании формулы окружности, получающейся от обычного векторного сложения v и c. Когда же их спрашиваешь, какое отношение формула кардиоиды имеет к кругам, получающимся на поверхности воды при движении поплавка, они разводят руками»

Я могу ответить на этот Ваш вопрос. Сначала вопросом: «А какое отношение имеют сами круги от поплавка на поверхности воды к формуле связи излучаемой и принимаемой частот волн?» Потом примером. Есть такая старая задача: написать в системе отсчета дороги формулу траектории мухи, сидящей на спице колеса, движущегося без скольжения с постоянной скоростью v по этой ровной дороге.

Ответ на эту задачу известен – получается циклоида. Таким образом, неподвижный наблюдатель на дороге видит муху, двигающуюся по циклоиде, и формула наблюдаемого движения мухи не является формулой окружности (хотя в системе отсчета, связанной с осью колеса, муха двигается по окружности).

Точно также для неподвижного наблюдателя, слышащего шум пролетающего мимо самолета, формула принимаемой частоты звуковых волн не обязана быть формулой окружности (хотя сами волны распространяются в воздушной среде по окружности).

И неподвижный наблюдатель на берегу реки зафиксирует колебания воды у берега по формуле кардиоиды от проплывающего по реке поплавка (хотя сами волны от поплавка расходятся по окружности).

А вот то, что формула окружности не может быть формулой Доплера для неподвижного наблюдателя и двигающегося источника, я покажу позже, в ходе анализа Вашей статьи.

6-й комментарий Акимова

При рассмотрении эффекта Доплера нужно четко различать то, что существует объективно, т.е. независимо от наблюдения за волновым процессом, и то, что видит наблюдатель (воспринимает датчик), находясь в какой-либо конкретной точке. Окружности на поверхности воды – это физическая данность. Их можно зафиксировать, например, фотоаппаратом, поднятым высоко над поверхностью воды. Могло случиться так, что вместо кругов на воде фотоаппарат зафиксировал бы эллипсы. Тогда нам пришлось бы сначала выводить математическое выражение для эллипса.

В точке А, выбранной на произвольной окружности (рис. 6 или 8), вообще говоря, никакого наблюдателя может и не быть. Эта точка является вспомогательной и служит для получения математического выражения. Однако если в точке А всё же появится покоящийся наблюдатель, то выражение (4) не изменится, так как оно вполне позволяет найти воспринимаемую длину волны (на линии АВ) в зависимости от конкретного угла наблюдения (угол θ). Не правильно думать, что с появлением покоящегося наблюдателя (датчика), выражение (4) непременно изменится. Нет, оно останется в силе. Непосредственная геометрия чертежа подтверждает такой вывод. Пример с мухой на вращающемся колесе здесь не подходит, так как ему отвечает совершенно другая геометрическая картинка.

Но ситуация радикально изменится, если начнет двигаться наблюдатель. Пусть источник покоится, тогда вся скобка (она обозначена буквой F) в выражении (4) для него окажется в знаменателе, т.е. для покоящегося наблюдателя будет справедливо выражение λ' = λ/F [ 2 ]. И это уже не является уравнением окружности. Здесь Ваш аргумент начинает работать в полную силу: длина волны, распространяющаяся в среде, будет отличаться от длины волны, которую воспринимает датчик. Чтобы вывести общее выражение для одновременного движения источника и приемника нужно обратиться к файлу [2]; там сказано следующее.

Надо различать три длины волна: λ0 – собственная длина волны источника колебаний, λ1 – длина волны колеблющейся среды и λ2 –длина волны, воспринимаемая приемником. Приемник ничего "не знает" об источнике – движется он или покоится – и какова его собственная частота λ0. Он воспринимает колебание среды λ1 в конкретной точке как автономный процесс. Без наличия среды никакого эффекта Доплера наблюдаться не будет. Чтобы найти результирующую длину волны лямбда-2 от совместного движения источника и приемника, нужно первое выражение для λ1 подставить во второе для λ2, получим: λ2 = λ0 × F1/F2.

Мне кажется, что Ваше искаженное представление об эффекте Доплера возникло потому, что Вы берете во внимание только два фактора, выраженных через λ0 и λ2. Третий фактор, λ1, который непосредственно связан со средой, Вы не замечаете. Это, в свою очередь, происходит из-за Вашей недооценки роли среды при распространении волн, особенно, оптических.


 

Hosted by uCoz