О формуле, описывающей классический эффект Доплера
Олег Акимов
Напомним, что называется эффектом Доплера. Если источник звуковых или световых волн покоится относительно однородной среды, где распространяются колебания, то длина волны λ (λ — расстояние межу двумя одинаковыми фазами колебаний) по всем направлениям будет одной и той же. Но стоит источнику колебаний сообщить движение в каком-то заданном направлении, как тут же длина волны будет меняться в зависимости от величины скорости источника и направления приёма волн. Изменение длины волны произойдет и в том случае, если источник покоится, а приёмник перемещается. Поскольку длина волны ( λ ), период ( T ) и частота колебаний ( f ) взаимосвязаны ( λ = c/f = cT ), то можно говорить об изменении T и f. Для анализа проблемы нам достаточно рассмотреть движущимся только источник и оперировать λ, а затем полученные результаты распространить на приёмник, T и f.
Со школьной скамьи нам знакома нехитрая формула, которой пользуются и профессиональные ученые:
. (1)
Формула (1) описывает принятую длину волны ( λ' ), если известна собственная длина волны ( λ ) движущегося с относительной скоростью ( β = v/c ) источника колебаний и угол между векторами v и c ( φ ). Полный вывод формулы (1) приводится в Приложении к данной статье, из которого следует, что она является приближенным математическим выражением. Ее вывод основывается на предположении, что расстояние между источником и приемником велико по сравнению с длиной волны.
Давайте зададимся вопросом: как будет выглядеть математическое выражение, когда источник и приемник находятся вблизи друг друга? В справочниках и учебниках по физике ничего не говорится о случаях, когда на промежутке между источником колебания и приемником укладывается всего одна, две или три длины волны. Мы не знаем, можно ли пользоваться формулой (1), если между источником и приемником укладывается 100 длин волн, а может быть она дает недопустимую погрешность уже для 1000 длин волн? Другими словами, при изложении темы «Эффект Доплера» не указывается, во-первых, количественный критерий действия формулы (1) и, во-вторых, математическое выражение, которым необходимо воспользоваться, когда формула (1) не действует или дает слишком большую погрешность.
Вторая проблема, которая здесь возникает, формулируется следующим образом. Почему выражение (1) никак не реагирует на появление ударной волны, т.е. когда скорость источника становится больше скорости распространения колебаний ( β > 1 )? Еще в XIX столетии Эрнст Мах, изучая движение пули, движущейся в воздухе быстрее звука, установил, что угол при вершине конуса ударной волны определяется относительной скоростью β:
sin θ = 1/β = c/v (2)
Формулы (1) и (2) никак не связаны, хотя с точки зрения непрерывности физического процесса (монотонного увеличения скорости движения источника: v → ∞) выражение (2) является прямым следствием процесса, описываемого выражением (1).
Указанные проблемы можно легко разрешить, если вспомнить, что формула, описывающая эффект Доплера, представляет собой математическое выражение векторного сложения двух скоростей — v и c. Ниже дается простой вывод точной и универсальной формулы, справедливой для всех значений скорости движения источника (0 < v < ∞).
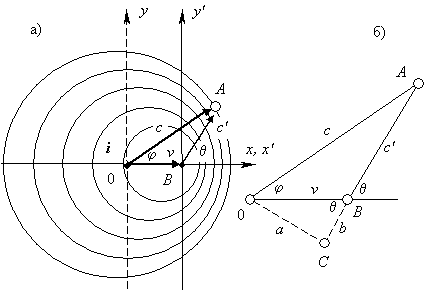 |
Рис. 1. Чертеж (а) представляет собой застывшее изображение процесса распространения волн при движущемся источнике колебаний ( i ). Пока волновой фронт, испущенный из точки 0, дойдет до точки А, источник колебаний i окажется в точке В. Чтобы найти выражения для векторной суммы векторов v и c, на чертеже (б) показан вспомогательный прямоугольный треугольник.
На рис. 1а вычерчен застывший в произвольный момент динамический процесс распространения волн. На одной из окружностей — неважно какой, поскольку все треугольники 0АВ будут подобными, — выбрана точка А. Стороны треугольника 0А и 0В соответствуют скоростям v и c; нужно по двум сторонам треугольника 0АВ найти третью — АВ. Для решения этой задачи треугольник 0АВ достраиваем до прямоугольного 0АС, как показано на рис. 1б. Из последнего чертежа находим отрезки a = v sin θ и b = v cos θ. По теореме Пифагора составляем равенство:
.
Если в последнее выражение подставить значения a и b, получим искомую скорость c' :
. (3)
Умножая обе части равенства (3) на период колебаний Т, получаем изменившуюся за счет эффекта Доплера длину волны λ', которую удобно выразить через параметр β:
. (4)
Формула (4) есть истинное, абсолютно точное выражение, описывающее эффект Доплера для любых значений параметра β. То, что формула (4) является именно выражением для суммы двух векторов v и c, можно легко убедиться, если ее представить через угол φ между v и c. Для этого нужно к треугольнику 0АВ применить теорему косинусов:
. (5)
С точки зрения математики выражения (4) и (5) отражают один и тот же математический факт, однако с точки зрения физики было бы ошибкой считать φ углом наблюдения; им является угол θ. Это прекрасно видно в случае, когда возникает ударная волна. На рис.2 видно, что конус ударной волны перемещается вместе с источником колебаний. Значит, для получения формулы Маха (2) и тесно связанной с ней формулой (4) нужно перейти из неподвижной системы координат (x, y) в штрихованную систему координат (x', y'), начало которой совмещено с движущимся источником волн.
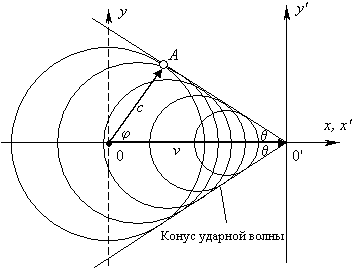 |
Рис. 2. Чертеж, позволяющий получить формулу (2) для определения угла θ при вершине конуса ударной волны
Если вместо теоремы косинусов воспользоваться теоремой синусов, которая дает равенство: sin(θ – φ) = βsinθ, а затем эти синусы выразить через косинусы (подробности здесь), то можно получить еще одно математическое выражение, в котором будут фигурировать уже как угол наблюдения (θ), так и угол между скоростями v и c (φ):
λ' = λ[cos(θ – φ) – βcosθ] (6)
Из выражения (6) следует: чем меньше разность между углами: (θ – φ) → 0, тем с большим правом мы можем пользоваться традиционной формулой (1).
Для получения формулы (4) никакого наблюдателя или приемника не требуется. Система концентрических колец со смещенными центрами образуется и без них. Главное, что здесь нужно, это выразить произвольно взятую окружность корректным образом. Старая формула (1), как мы увидим ниже, является уравнением кардиоиды в полярной системе координат, а полученное нами выражение (4) является уравнением окружности. Для этого уравнения угол θ является свободным параметром или аргументом, а воспринимаемая приемником длина волны λ' или сторона АВ, изображенного на рис. 1а треугольника, является радиус-вектором или функцией для указанного аргумента.
В самом деле, из рис. 1а можно записать:
0А = λ, 0В = βλ и АВ = λ'.
В декартовой системе координат (x', y') с началом в центре В, уравнение окружности выглядит следующим образом:
(x' + βλ)2 + (y')2 = λ2.
Произведем переход от декартовых координат к полярным по формулам:
(λ')2 = (x')2 + (y')2, x' = λ'cosθ, y' = λ'sinθ.
Тогда наше уравнение окружности будет иметь вид:
(λ')2 + 2βλλ'cosθ – λ2(1 – β2) = 0.
Перед нами обыкновенное квадратное уравнение, решая которое относительно неизвестной λ', мы получаем формулу (4).
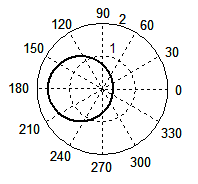
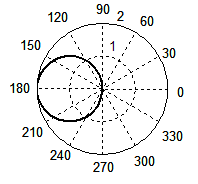
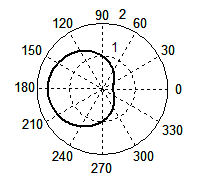
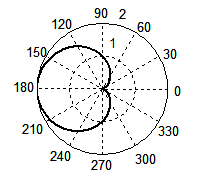
Окружность получается и в том случае, если для функции λ' выражения (4) построить графики зависимости от аргумента θ, меняющийся в пределах от 0 до 2π. Графики этой зависимости (рис. 3) для β = 3/4 (а) и β = 1 (б) лишний раз подтверждает, что мы имеем дело действительно с окружностями, которые можно видеть, например, на поверхности озера, когда по ней бежит водомер. Однако традиционное выражение (1), приводимое во всех сегодняшних справочниках и учебниках, окружности не дает. При тех же значениях β волновой фронт как функция λ' от аргумента θ порождает кривые (в, г), которые в математике называются кардиоидами.
 (a) (a) |
 (б) (б) |
 (в) (в) |
 (г) (г) |
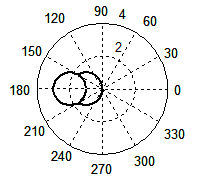 (д) (д) |
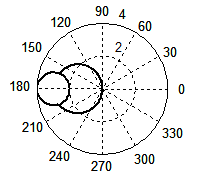 (е) (е) |
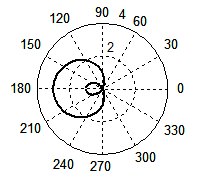 (ж) (ж) |
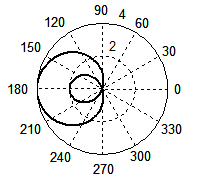 (з) (з) |
Рис. 3. Форма волнового фронта при Доплер-эффекте, рассчитанная по формуле (4) при β = 3/4 (а), β = 1 (б); по формуле (1) при β = 3/4 (в), β = 1 (г). Для случая появления ударной волны: по формуле (4) при β = 2 (д), β = 3 (е); по формуле (1) при β = 2 (ж), β = 3 (з).
Самое важное, что точная формула (4) прекрасно работает и в случае ударной волны. Волновой фронт сохраняет форму окружности при любом значении β, в частности, при β = 2 (д) и β = 3 (е). Обратите внимание, радиусы обеих окружностей одинаковые и равны единице, только в случае (д) центр окружности отнесен на расстояние, равное двум, а для случая (е) — трем, что вполне логично. Таким образом, формула (4) в точности следует тому, что повсеместно наблюдается в природе: с увеличением скорости движения источника слева направо круги, естественно, всё дальше и дальше смещаются влево от источника. Формула Маха (2) также естественно вытекает из формулы (4). Если подкоренное выражение окажется отрицательным, то корни из него будут мнимыми. Мнимые величины не имеют физического смысла, поэтому на подкоренное выражение накладывается условие:
1 – β2 sin2θ ≥ 0, sinθ ≤ |±1/β| или θ ≤ arcsin |±1/β|.
На графиках (д) и (е) показаны неполные окружности, которые не имеют определенного физического смысла. Тем не менее, эти мнимые волны были оставлены на чертеже, поскольку их концы точно указывают точки соприкосновения реальных волн с конусом ударной волны. На двух последних графиках изображены кривые, вычерченные в соответствии с традиционной формулой (1) при тех же значениях β = 2 (ж) и β = 3 (з). Как видим, ничего близкого с действительностью эти графики не имеют.
Обсуждаемая в данной работе проблема изложена в учебнике [1].
Приложение
Вывод традиционной формулы, описывающей
классический эффект ДоплераЗдесь мы покажем, что традиционная формула, описывающая эффект Доплера, не просто не точна, а, по сути дела, ошибочна. С этой целью вычертим рис. 4.
 |
Рис. 4. Чертеж, разъясняющий ошибочность вывода традиционной формулы Доплера для движущегося источника колебаний.
Итак, волна, испущенная из точки 0, пришла в точку А через время 0А/с. Следующая волна, народившаяся через период T после первой, испускается в точке, расположенной на расстоянии vT правее точки 0. Далее используется приближенное равенство углов φ = А0В и φ1, который возник при небольшом сдвиге источника колебаний. Вместо нового угла φ1 используется старый угол φ. За новое расстояние между источником и приёмником принимается величина, равная 0А – vTcosφ. Тогда новая волна придет в точку приёма А в момент времени T ' :
T ' = (0А – vTcosφ)/c = T(1 – βcosφ).
После умножения обеих частей этого равенства на с, приходим к традиционной формуле (1), у которой угол φ является углом наблюдения.
Ошибка в этих рассуждениях вполне очевидна. Да, действительно, время прохода первой волны ( Т ) от времени прохода второй волны (T ' ) отличается ненамного и приближённое равенство φ = φ1 здесь брать допустимо. И всегда между соседними углами разница небольшая, поэтому будет справедлива бесконечная цепочка равенств: φ = φ1, φ1 = φ2, φ2 = φ3 и т.д. Однако за большой промежуток времени ошибка набегает значительная и уже, например, равенство φ = φ100 будет слишком грубым.
Другими словами, формула (1) верна для длин волн, испущенных источником, который переместился на крохотное расстояние. Если же он сдвигается на большие расстояния, в частности, на расстояние 0В, то формулу (1) уже нельзя использовать, как и нельзя считать в ней параметр φ углом наблюдения. Формула (4) дает модуль векторного сложения двух скоростей v и с, а в формуле (1) фигурирует только проекция вектора v на вектор с, которая была введена на самом начальном этапе вывода, когда записывалось выражение 0А – vTcosφ, или иначе, с – vcosφ. Естественно, что никаких окружностей формула (1) дать не может.
Таким образом, обобщенные формулы Доплера:
,
.
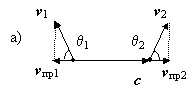
имеют дело не суммой двух векторов, а с их проекциями. Автор этих формул (он историкам науки не известен), очевидно, посчитал, если к относительным скоростям β1 и β2 приписать по соответствующему косинусу cosθ1 и cosθ2, то тем самым будет учтена всевозможная направленность векторов v1 и v2, Он думал, наверное, что на изменение длины волны λ' и частоты колебаний f ' может оказывать влияние лишь проекции скоростей v1 и v2 на вектор c, т.е. величины vпр1 и vпр2 (рис. 5), а не сами векторные разности: c – v1 и c – v2.
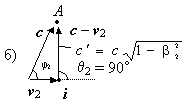
Рис. 5. Традиционно эффект Доплера объясняется за счет сложения вектора скорости распространения волны (c) с проекциями скоростей источника vпр1 и приемника vпр2 (а). Реально же необходимо производить действия не с проекциями скоростей, а с самими векторами v1 и v2. В частности, при движении только источника i изменение длины волны в направлении наблюдателя A произойдет пропорционально разности скоростей c – v2; формула же c – vпр2 была бы здесь ошибочной.
Трудно сказать, о чём думал автор традиционных формул, только пользоваться выражениями, которые вместо окружностей дают кардиоиды, далее невозможно. Реконструкция его рассуждений, отображаемая рис. 4 и рис. 5, возможно, была иной. Купряев Н.В. предложил [2] другой вариант вывода формулы (1).
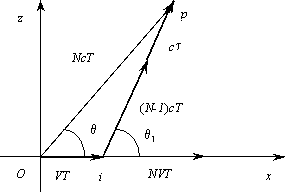
Пусть источник колебаний ( i ) движется со скоростью V вдоль оси x. Приемник колебаний находится в точке p, как показано на рис. 6. На расстоянии 0p между источником и приемником укладывается N длин волн (λ). Тогда за один период ( Т ) источник i переместится на расстояние VT.
Рис. 6. К выводу приближенной формулы (1) по Н.В. Купряеву.
Непосредственно из чертежа (рис. 6) Купряев Н.В. составляет выражение:
,
Решая его относительно τ, он получает:
.
Для нахождения частоты колебаний ν нужно найти предел от обратной величины τ:
В результате Купряев Н.В. получает традиционную формулу для эффекта Доплера приближенного характера:
.
,
где
— наблюдаемая частота,
— собственная частота излучения источника. Точная же формула для наблюдаемой частоты ν, которая получается из формулы суммы двух векторов v и c, выглядит иначе:
.
Как видим, Н.В. Купряев привел более общее, но вместе с тем и более сложное доказательство традиционной формулы Доплера. Он предполагает, что на отрезке пути от источника до приемника (на рис. 4 это расстояние 0А, на рис. 6 — 0Р) укладывается не одна волна, а множество — N. Причем традиционное выражение у него получится только при условии, если N → ∞. Чтобы лучше почувствовать разницу между последним выражением и предпоследним, обратимся к числам.
Пусть β = cosθ = 0,5 и собственная частота излучения равна νi = 100. Тогда по традиционной формуле наблюдаемая частота равна ν = 133,33. Теперь воспользуемся формулой, выведенной Н.В. Купряевым. Пусть на отрезке от источника до приемника укладывается тысяча длин волн, т.е. N = 1000. При этом значении N наблюдаемая частота равна ν = 133,22, что не намного отличается от результата, полученного по традиционной формуле. Если N = 100, разрыв слегка увеличивается: ν = 132,16. Но при N = 3, имеем уже ν = 66,67, а при N = 2 и N = 1 воспринимаемую частоту вообще невозможно определить, так как подкоренное выражение становится отрицательным, т.е. формула Н.В. Купряева перестает работать.
Если же вычисления вести по единственно правильной формуле, не зависящей от числа N, то получим ν = 153,56. И это не самое большое расхождение между результатами, которые дают две кривые — окружность и кардиоида. Сравните рис. 3б и рис. 3г (β = 1, cosθ = 0). На них видно, что когда кардиоида дает ν = 100, окружность даст ν = ∞ (λ = 0), что соответствует прохождению источником волн звукового барьера.
В связи с вышеизложенным, возникает вопрос: почему точная формула (4) не бала выведена с самого начала открытия эффекта Доплера? Ведь, казалось бы, эффект дает о себе знать повсюду, поскольку движущиеся источники и приемники волн встречаются и в воде, и в воздухе, и в космосе. Разве можно себе представить, чтобы столь нужная и вместе с тем ошибочная формула могла существовать более века? Понятно, что возникновение фронта ударной волны есть всего лишь следствие непрерывного возрастания скорости движущегося источника волн, испытывающих доплеровскую трансформацию. Тогда почему физики конца XIX – начала XX вв. не воспользовались формулой (4) и не увязали ее с формулой Маха (2)?
Дело в том, что формулой (1) в практических расчетах никто особенно и не пользуется. Из-за реальной неоднородности воды и воздуха, их непрерывной динамики инженеры пользуются специальными таблицами, составленными на основе эмпирических данных. Взгляните на рис. 7, где показаны слои земной атмосферы. С увеличением высоты над поверхностью Земли температура колеблется довольно в широком диапазоне, а это значит, что плотность воздуха тоже будет заметно колебаться. И это помимо того, что имеется естественный градиент давления, вызванный силой притяжения Земли: на каждые 20 километров высоты давление снижается примерно в 10 раз. Скорость распространения звука зависит от плотности и скорости перемещения воздуха, но из-за непредсказуемости погоды априорный теоретический расчет практически невозможен. На практике пользуются аппроксимированными выражениями линейного характера. Когда же нужна точность, прибегают к градуировке шкалы по эталону скорости, миную какие-либо математические выражения.
.
Рис. 7. Изменение плотности и температуры воздуха в зависимости от высоты над поверхностью Земли. Неравномерность нагревания атмосферы способствует общей циркуляции воздуха, которая влияет на погоду и климат Земли.
С количественной точки зрения картина выглядит следующим образом. Принятая скорость распространения акустических колебаний в воздухе при температуре t = 0°С и давлении P = 1 атм. равна v = 331,5 м/с. При повышении температуры воздуха на 10°С скорость звука увеличивается примерно на 6 м/с, так что при комнатной температуре (t = 20°С) скорость звука окажется равной 343 – 344 м/с. Напомним, скорость звука определяется формулой v = (μ/ρ)½, где μ – модуль упругости и ρ – плотность воздуха. Порывистый ветер с Δv = 3 – 5 м/с способен заметно исказить круговой волновой фронт не только за счет скорости перемещения среды, но и за счет локального изменения в ней давления в 2 – 4 раза. Однако максимальные искажения дины волны или частоты колебаний происходят за счет перепада давления в прилегающей области к движущемуся излучателю: давление повышается по ходу его движения и понижается в противоположном направлении. Таким образом, сколько-нибудь точное измерение скорости движущихся в воздухе объектов (автомобилей и самолетов) на основе звукового Доплер-эффекта проблематично. Поэтому, например, милицейские радары (Искра-1, ПКС-4, ЛИСД-2, Барьер-2М, Сокол, Беркут и т.д.) не работают в звуковом диапазоне, а используют электромагнитные излучатели в Х- и К-диапазоне (10 – 100 ГГц).
Ситуация с водной стихией выглядит еще более удручающе, так как скорость распространения акустических волн в морской воде составляет почти полторы тысячи метров в секунду (v = 1490 м/с при t = 20°С). Следовательно, для точной количественной оценки Доплер-эффекта излучатель должен перемещаться с гораздо большей скоростью, чем в воздухе, что сделать крайне затруднительно. О сложности вычислений в случае неоднородной и постоянно движущейся среды, каковой является атмосфера земли и мировой океан, рассказывается, например, в книге Д.И. Блохинцева [3]. Автор рассматривает проблему преимущественно с теоретической точки зрения, причем подходит к ней со стороны слишком абстрактной и формализованной. Полученные им громоздкие выражения трудно поддаются физической интерпретации. Поскольку Блохинцеву не известна точная формула Доплера, то все его теоретические рассуждения, с позиции рассматриваемого здесь вопроса, не имеют большой ценности. Книга значительно выиграла бы, если бы автор больше привел эмпирического материала. Тем не менее, Блохинцеву удалось обрисовать те трудности, которые поджидают исследователя, посвятившего себя данной тематике.
Таким образом, экспериментальная проверка точной формулы (4), описывающей эффект Доплера, на основе акустических колебаний, распространяющихся в воздушной и водной среде так же сложна, как и на основе электромагнитных (световых) волн. Но природа подарила нам уникальный случай, когда эффект Доплера становится отлично видимым, что называется, невооруженным глазом. Это — распространение волн на поверхности воды от перемещающегося по водной глади поплавка, равномерно погружающегося в воду и выныривающего из нее. В этом случае мы наблюдаем динамическую картину (рис. 8), которая в точности повторяет «застывший» процесс, запечатленный на рис. 1.
 |
 |
| Рис. 8а. Источник возбуждения среды движется слева направо со скоростью меньше скорости распространения возбуждения (v < c). | Рис. 8б. Источник возбуждения движется быстрее, чем распространяется возбуждение в среде (v > c). При этом возникает так называемый конус ударной волны |
Противники точной формулы (4) из-за очевидности и простоты получения картины называют данную физическую модель Доплер-эффекта чисто геометрической и не хотят присваивать ей физический статус. Эти требования нельзя признать законными. Прежде им необходимо доказать, что волновой фронт для реальных колебаний не дает окружности и сферы; для двумерного случая они должны обосновать существование кардиоиды. Разумеется, этого доказать они не в силах, а инерция мышления не позволяет им отказаться от старой формулы (1) в пользу новой (4).
Вопросы эффекта Доплера рассматриваются также на следующих страницах:
- Введение в акустику. Природа звука и ультразвука
- Введение в конструктивную физику
- О формуле, описывающей классический эффект Доплера
- Ошибочность релятивистской формулы Доплера
- Квантовая теория Доплер-эффекта
- Эксперимент Майкельсона – Морли
- Лекция 4. Эффект Доплера
- Часто задаваемые вопросы по эффекту Доплера
- Идиотский расчет эффекта Доплера
- Использование в медицине поперечного эффекта Доплера для ультразвуковой диагностики сердечно-сосудистой системы
- Эффект сдвига воспринимаемой длины волны в красную область
- Моделирование волновых процессов. Эффект Доплера
1. Акимов О.Е. Естествознание: Курс лекций. – М.: ЮНИТИ-ДАНА, 2001.
2. Купряев Н.В. Классический эффект Доплера. SciTecLibrary.ru, #8803, 25.12.2007.
3. Блохинцев Д.И. Акустика неоднородной движущейся среды. Второе издание. – М.: Наука, 1981.