Идиотский расчет эффекта Доплера

Один из моих читателей прислал мне pdf-файл следующего содержания

Проанализируем пример, который О. Акимов рекомендовал "релятивистам": «всем формалистам-феноменалистам, лишенным воображения, настоятельно рекомендуется с помощью циркуля и линейки вычертить рисунок с движущимся источником. Если они возьмут λ = 30 мм и β₂ = 2/3, то при θ₂ = ± 90° получат λ' = 22,4 мм, что как раз и соответствует уменьшению исходной длины волны λ в раз. Случай, когда λ' = λ, возможен, но он произойдет при другом угле наблюдения: θ₂ = ± 110°».

Для большей наглядности представим пример Акимова в таком виде. Пусть мы находимся на какой-то планете на поверхности океана из неизвестной жидкости, на которой волны распространяются со скоростью с = 30 ед/ев (где «ед» — единица длины, а «ев» — единица времени, принятые на той планете). Низко над поверхностью океана пролетает самолет по прямой линии со скоростью 20 ед/ев и каждую ев выбрасывает бомбу, от взрыва которой по поверхности океана распространяется взрывная волна. В стороне от курса самолета, на расстоянии 200 ед по перпендикуляру, находится Наблюдатель; перпендикуляр пересекает курс самолета в точке 8-го взрыва.

Введем систему координат, как показано на рис.1. Время отсчитываем от момента первого взрыва в точке x = 0, y = 200. Наблюдатель находится в точке x = 140, y = 0. Взрывные волны будем идентифицировать по x-координате их центра: «волна Ц-0», «волна Ц-20» и т.д. Прямую x = 140 будем называть «меридианом наблюдателя»; прямую y = 200 "курсом самолета".

Нажмите для увеличения

Рис. 1. Взрывные волны в момент t = 8 ев после начала отсчета

На Рис.1 изображена ситуация, когда самолет находится на своем курсе в точке x = 160 (и выбрасывает 9-ю бомбу). В этот момент произошли уже 8 взрывов, и по океану распространяются 8 взрывных волн. Первая из них вот-вот достигнет Наблюдателя.

Определим путь s, который каждая волна прошла по меридиану наблюдателя. В общем случае это катет прямоугольного треугольника, в котором второй катет образует расстояние l центра взрыва до меридиана наблюдателя по курсу самолета, а гипотенуза – радиус волны r. Поэтому по теореме Пифагора имеем:

s = √ ( r ² – l ² ).

Посчитаем, идентифицируя пути теми же индексами, что и волны (таблица 1):

Таблица 1

s₀ = √(240² – 140²) = √38000 = 194,93588689617927813676826399799 ед
s₂₀ = √(210² – 120²) = √29700 = 172,33687939614085979551834404657 ед
s₄₀ = √(180² – 100²) = √22400 = 149,66629547095765542334994929266 ед
s₆₀ = √(150² – 80²) = √16100 = 126,88577540449520380193772746089 ед
s₈₀ = √(120² – 60²) = √10800 = 103,92304845413263761164678049035 ед
s₁₀₀ = √(90² – 40²) = √6500 = 80,622577482985496523666132303038 ед
s₁₂₀ = √(60² – 20²) = √3200 = 56,568542494923801952067548968388 ед
s₁₄₀ = √(30² – 0²) = √900 = 30 ед

Иррациональные числа, разумеется, округлены, но с той точностью, какую выдает калькулятор Windows.

Посчитаем расстояния λ между волнами по меридиану наблюдателя (таблица 2).

Таблица 2

λ_0–20 = 22,599007500038418341249919951424 ед
λ_20–40 = 22,670583925183204372168394753906 ед
λ_40–60 = 22,780520066462451621412221831767 ед
λ_60–80 = 22,962726950362566190290946970543 ед
λ_80–100 = 23,300470971147141087980648187315 ед
λ_100–120 = 24,05403498806169457159858333465 ед
λ_120–140 = 26,568542494923801952067548968388 ед

Видно, что, если смотреть от Наблюдателя, расстояния между волнами всё увеличиваются. (Это и понятно: уменьшается угол между меридианом наблюдателя и направлением на центр волны). Более округленные значения λ написаны на Рис.1 вместе с y-координатами точек пересечения волн и меридиана наблюдателя.

Посчитаем интервалы времени, через какие волны будут достигать Наблюдателя. Для этого нам надо сначала определить расстояние d от наблюдателя до центров взрывов. Это гипотенуза прямоугольного треугольника, в котором одним катетом является расстояние l центра взрыва до меридиана наблюдателя по курсу самолета, а вторым катетом постоянное расстояние h Наблюдателя до курса самолета по меридиану (200 ед). По теореме Пифагора d = √(200² + l²) (таблица 3):

Таблица 3

d₀ = √(200² + 140²) = 244,13111231467405903795710513246 ед
d₂₀ = √(200² + 120²) = 233,23807579381201883496611510182 ед
d₄₀ = √(200² + 100²) = 223,60679774997896964091736687313 ед
d₆₀ = √(200² + 80²) = 215,40659228538016125002841966161 ед
d₈₀ = √(200² + 60²) = 208,80613017821100359515508045096 ед
d₁₀₀ = √(200² + 40²) = 203,96078054371139320112896436091 ед
d₁₂₀ = √(200² + 20²) = 200,99751242241780540438529825519 ед
d₁₄₀ = √(200² + 0²) = 200 ед

Так как скорость волны с = 30 ед/ев, а каждый следующий взрыв происходит 1 ев после предыдущего, то волны достигнут Наблюдателя в такие моменты после начала отсчета времени (таблица 4):

Таблица 4

t₀ = 0 + d₀/c = 8,13770374382246863459857017108 ев
t₂₀ = 1 + d₂₀/c = 8,7746025264604006278322038367267 ев
t₄₀ = 2 + d₄₀/c = 9,45355992499929898803057889577 ев
t₆₀ = 3 + d₆₀/c = 10,180219742846005375000947322053 ев
t₈₀ = 4 + d₈₀/c = 10,960204339273700119838502681697 ев
t₁₀₀ = 5 + d₁₀₀/c = 11,798692684790379773370965478697 ев
t₁₂₀ = 6 + d₁₂₀/c = 12,699917080747260180146176608503 ев
t₁₄₀ = 7 + d₁₄₀/c = 13,666666666666666666666666666667 ев

Наблюдатель будет считать, что волны имеют длину λ = ct_i , где t_i интервал времени между двумя волнами. Он получит такие длины волн (таблица 5):

Таблица 5

λ_0–20 = 19,10696347913795979700900996938 ед
λ_20–40 = 20,36872195616695080595125177132 ед
λ_40–60 = 21,7997945354011916091110527884 ед
λ_60–80 = 23,3995378928308423451266607892 ед
λ_80–100 = 25,15465036550038960597388391 ед
λ_100–120 = 27,0367318787064122032563338943 ед
λ_120–140 = 29,0024875775821945956147017448 ед

Это и есть эффект Доплера для приближающегося (под углом) источника. Рассчитаем то же самое для удаляющегося источника.

Нажмите для увеличения

Рис. 2. Взрывные волны в момент t = 15 ев после начала отсчета

На Рис.2 изображена ситуация, когда самолет находится на своем курсе в точке x = 300 (и выбрасывает 16-ю бомбу). На рисунке отображены волны от последних 8-и взрывов.

На меридиане наблюдателя (в пределах рисунка) нет уже такого количества волн, как во время приближения самолета. Пути, пройденные волнами по меридиану (таблица 6):

Таблица 6

s₁₄₀ = √(240² – 0²) = √57600 = 240 ед
s₁₆₀ = √(210² – 20²) = √43700 = 209,04544960366872333964101859373 ед
s₁₈₀ = √(180² – 40²) = √30800 = 175,49928774784244120812776614833 ед
s₂₀₀ = √(150² – 60²) = √18900 = 137,47727084867520019764141581184 ед
s₂₂₀ = √(120² – 80²) = √8000 = 89,442719099991587856366946749251 ед

Посчитаем расстояния λ между волнами по меридиану наблюдателя (таблица 7):

Таблица 7

λ_140–160 = 30,9545503963312766603589814063 ед
λ_160–180 = 33,5461618558262821315132524454 ед
λ_180–200 = 38,0220168991672410104863503365 ед
λ_200–220 = 48,03455174868361234127446906255 ед

Расстояния уменьшаются по мере отдаления от курса самолета.

Найдем расстояния d от наблюдателя до центров взрывов. Они в данном примере симметричны расстояниям в картине приближения самолета (потому, что меридиан наблюдателя проходит через центр одного из взрывов) (таблица 8):

Таблица 8

d₀ = √(200² + 140²) = 244,13111231467405903795710513246 ед
d₂₀ = √(200² + 120²) = 233,23807579381201883496611510182 ед
d₄₀ = √(200² + 100²) = 223,60679774997896964091736687313 ед
d₆₀ = √(200² + 80²) = 215,40659228538016125002841966161 ед
d₈₀ = √(200² + 60²) = 208,80613017821100359515508045096 ед
d₁₀₀ = √(200² + 40²) = 203,96078054371139320112896436091 ед
d₁₂₀ = √(200² + 20²) = 200,99751242241780540438529825519 ед
d₁₄₀ = √(200² + 0²) = 200 ед
d₁₆₀ = √(200² + 20²) = 200,99751242241780540438529825519 ед
d₁₈₀ = √(200² + 40²) = 203,96078054371139320112896436091 ед
d₂₀₀ = √(200² + 60²) = 208,80613017821100359515508045096 ед
d₂₂₀ = √(200² + 80²) = 215,40659228538016125002841966161 ед
d₂₄₀ = √(200² + 100²) = 223,60679774997896964091736687313 ед
d₂₆₀ = √(200² + 120²) = 233,23807579381201883496611510182 ед
d₂₈₀ = √(200² + 140²) = 244,13111231467405903795710513246 ед

Так как скорость волны с = 30 ед/ев, а каждый следующий взрыв происходит 1 ев после предыдущего, то волны достигнут Наблюдателя в такие моменты после начала отсчета времени (таблица 9):

Таблица 9

t₁₄₀ = 7 + d₁₄₀/c = 13,666666666666666666666666666667 ев
t₁₆₀ = 8 + d₁₆₀/c = 14,699917080747260180146176608503 ев
t₁₈₀ = 9 + d₁₈₀/c = 15,798692684790379773370965478697 ев
t₂₀₀ = 10 + d₂₀₀/c = 16,960204339273700119838502681697 ев
t₂₂₀ = 11 + d₂₂₀/c = 18,180219742846005375000947322053 ев
t₂₄₀ = 12 + d₂₄₀/c = 19,45355992499929898803057889577 ев
t₂₆₀ = 13 + d₂₆₀/c = 20,774602526460400627832203836727 ев
t₂₈₀ = 14 + d₂₈₀/c = 22,13770374382246863459857017108 ев

Наблюдатель будет считать, что волны имеют длину λ = ct_i , где t_i интервал времени между двумя волнами. Он получит такие длины волн (таблица 10):

Таблица 10

λ_140–160 = 30,9975124224178054043852982552 ед
λ_160–180 = 32,9632681212935877967436661057 ед
λ_180–200 = 34,84534963449961039402611609 ед
λ_200–220 = 36,6004621071691576548733392108 ед
λ_220–240 = 38,2002054645988083908889472116 ед
λ_240–260 = 39,6312780438330491940487482285 ед
λ_260–280 = 40,8930365208620402029909900308 ед

Это и есть эффект Доплера для удаляющегося (под углом) источника.

Теперь определим углы, задействованные в нашей картине.

Нажмите для увеличения

Рис. 3. θ — углы между курсом самолета и направлением на Наблюдателя;
γ — углы, под которыми Наблюдатель видит расстояние между взрывами

Углы θ — это arc tan соотношения h/l, где h = 200 — расстояние между Наблюдателем и курсом самолета, а l — расстояние до меридиана (таблица 11).

Таблица 11

θ₀ = arc tan 200/140 = 55,007979801441337893077108969542 °
θ₂₀ = arc tan 200/120 = 59,036243467926478582892320159163 °
θ₄₀ = arc tan 200/100 = 63,434948822922010648427806279547 °
θ₆₀ = arc tan 200/80 = 68,198590513648188229755133913056 °
θ₈₀ = arc tan 200/60 = 73,300755766006378159631152820016 °
θ₁₀₀ = arc tan 200/40 = 78,69006752597978691352549456166 °
θ₁₂₀ = arc tan 200/20 = 84,289406862500357487304118651766 °
θ₁₄₀ = arc tan 200/0 = 90 °
θ₁₆₀ = arc tan 200/–20 = 95,710593137499642512695881348234 °
θ₁₈₀ = arc tan 200/–40 = 101,30993247402021308647450543834 °
θ₂₀₀ = arc tan 200/–60 = 106,69924423399362184036884717998 °
θ₂₂₀ = arc tan 200/–80 = 111,80140948635181177024486608694 °
θ₂₄₀ = arc tan 200/–100 = 116,56505117707798935157219372045 °
θ₂₆₀ = arc tan 200/–120 = 120,96375653207352141710767984084 °
θ₂₈₀ = arc tan 200/–140 = 124,99202019855866210692289103046 °

Углы γ — это разность двух соседних углов θ (таблица 12):

Таблица 12

γ_0–20 = θ₂₀ – θ₀ = 4,02826366648514068981521118962 °
γ_20–40 = θ₄₀ – θ₂₀ = 4,39870535499553206553548612038 °
γ_40–60 = θ₆₀ – θ₄₀ = 4,76364169072617758132732763351 °
γ_60–80 = θ₈₀ – θ₆₀ = 5,10216525235818992987601890696 °
γ_80–100 = θ₁₀₀ – θ₈₀ = 5,38931175997340875389434174165 °
γ_100–120 = θ₁₂₀ – θ₁₀₀ = 5,5993393365205705737786240901 °
γ_120–140 = θ₁₄₀ – θ₁₂₀ = 5,71059313749964251269588134824 °
γ_140–160 = θ₁₆₀ – θ₁₄₀ = 5,710593137499642512695881348234 °
γ_160–180 = θ₁₈₀ – θ₁₆₀ = 5,59933933652057057377862409007 °
γ_180–200 = θ₂₀₀ – θ₁₈₀ = 5,3893117599734087538943417416 °
γ_200–220 = θ₂₂₀ – θ₂₀₀ = 5,102165252358189929876018907 °
γ_220–240 = θ₂₄₀ – θ₂₂₀ = 4,7636416907261775813273276335 °
γ_240–260 = θ₂₆₀ – θ₂₄₀ = 4,3987053549955320655354861204 °
γ_260–280 = θ₂₈₀ – θ₂₆₀ = 4,0282636664851406898152111896 °

Акимов писал: "... находим формулу для измененной длины волны λ' для случая движения источника i при покоящемся наблюдателе A:

λ' = λcos (θ₂ – φ₂) + β₂λcos(π – θ₂) или λ' = λ[cos (θ₂ – φ₂) – β₂cos θ₂].

Обратите внимание, в чем главное отличие последней формулы от традиционно принятой в физике:

λ' = λ(1 – β₂cos θ₂)...

У нас θ₂ = 2/3 (соотношение скорости самолета и скорости распространения волн)...

*
*   *

Дальше, Олег, мне не понятно, как считать по Вашим формулам... Является ли угол θ₂ – φ₂ тем же углом γ или чем-то другим?

Мне не понятно также, что такое вообще λ', вычисляемое Вашей формулой, какой ее физический смысл в терминах данного выше примера? Ведь единственные длины волн (расстояния между двумя фронтами волн), реально доступные Наблюдателю, – это величины, рассчитанные в таблице 5 и таблице 10. Но эти величины не будут совпадать с величинами, измеренными по той или иной прямой. И по какой прямой мерить: например, для длины волны λ_40–60 мерить по прямой от Наблюдателя к центру взрыва x = 40 или к центру взрыва x = 60, или еще по какой-то другой прямой?

Мне не ясно также, в каком случае по-Вашему будет наблюдаться поперечный эффект Доплера классической физики. Вы писали: "Для перемещающегося точечного источника (4.1б) можно вычертить векторную диаграмму, представленную на рис. 4.2б. Пунктирная линия демонстрирует, что при угле наблюдения θ₂ = ± 90° поперечный эффект Доплера очевидным образом дает о себе знать, так как λ' < λ.

Вот эти рисунки:

Рис. 4.1. Эффект Доплера: источник колебаний i покоится, приемник A движется со скоростью v₁ по направлению к источнику (а); приемник A покоится, источник i движется со скоростью v₂ по направлению к приемнику (б). В обоих случаях будет наблюдаться изменение длины волны λ.

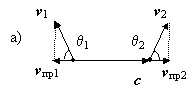
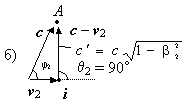
Рис. 4.2. Традиционно эффект Доплера объясняется за счет сложения вектора скорости распространения волны (c) с проекциями скоростей источника v_пр1 и приемника v_пр2 (а). Реально же необходимо производить действия не с проекциями скоростей, а с самими векторами v₁ и v₂. В частности, при движении только источника i изменение длины волны в направлении наблюдателя A произойдет пропорционально разности скоростей c – v₂; формула же c – v_пр2 была бы здесь ошибочной. Поэтому, если угол наблюдения равен θ₂ = ± 90°, то наблюдатель A зафиксирует поперечный эффект Доплера, т.е. зарегистрирует уменьшение длины волны ( λ' < λ ), пропорциональное разности скорости распространения колебаний c и скорости источника v₂ (б).

Которая пунктирная линия демонстрирует поперечный эффект Доплера? Видимо, та, что на рис. 4.1б. Но там наблюдатель А находится (в терминах моего примера) на курсе самолета и ничего не наблюдает по пунктирной линии. Если же его переместить в сторону от курса самолета, то ситуация сведется к моему рис. 1 или 2, и Ваша пунктирная линия превратится в мой «меридиан наблюдателя». Будет ли на нем поперечный эффект Доплера? Или поперечный эффект Доплера наблюдается, когда оба (самолет и наблюдатель) движутся относительно среды? Словом, для дальнейшего анализа предложенного Вами примера мне требуются уточнения, что, собственно, Вы имеете в виду.

*
*   *


Мой читатель свой pdf-файл сопроводил коротким письмом:

Здравствуйте, Олег!
Я три месяца не занимался Вашими книгами, но недавно вернулся к ним и среди прочего попытался просчитать предложенный Вами в книге "Естествознание" пример. Однако при этой попытке у меня возникли некоторые неясности, изложенные в прикрепленном файле Voprosy.pdf. Не можете ли Вы ответить на заданные там вопросы?

Я ответил так:

Здравствуйте, ***.
Прошла четверть века, как я рассказываю людям об эффекте Доплера. У меня имеется некоторый опыт относительно того, как они воспринимают это явление. Большая часть не в состоянии представить пространственную динамику волн, сколько бы я им не растолковывал. Небольшая часть понимает эффект сразу и без моей помощи. Мне абсолютно чужд тот путь, который Вы проделали, пытаясь усвоить изложенный мной материал. Ваши расчеты кажутся мне нелепыми, запутывающими суть дела, а вопросы тупиковыми. Прежде чем что-то вычислять, нужно представлять себе общую картину явления, которой у Вас нет.

Адекватное понимание появляется тогда, когда данный эффект рассматривают с разных сторон. Вы воспользовались единственным источником (книгой «Естествознание»), где это явление рассмотрено с одной позиции. Но я написал еще несколько пояснений, в которых даются другие подходы. Воспользуйтесь ими. Откройте страницу:

http://sceptic-ratio.narod.ru/fi.htm

Здесь имеется обращение: «Уважаемые старшеклассники и студенты…». Прочтите его полностью и затем переходите к беглому просмотру указанных там страниц. Поначалу не слишком углубляйтесь в детали. Схватите общее, а уж потом переходите к частностям.
Желаю успеха, Олег.

Мой трудолюбивый читатель воспроизвел написанное мной обращение:

Уважаемые старшеклассники и студенты,
прежде чем заняться проблемами физики,
уясните для себя суть эффекта Доплера

Она раскрывается через понимание волновой диаграммы 1, где изображены круговые или сферические (для 3D-пространства) волны от движущегося источника колебаний.

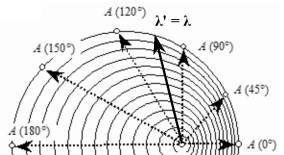Диаграмма 1. Картина волн, расходящихся от движущегося вправо источника колебаний. Объективно мы видим, что для точки А (0°) λ ' = λ (1 – β), для точки А (180°) λ ' = λ (1 + β). Вопрос: при каком угле θ можно будет наблюдать равенство λ ' = λ? Может быть, при θ = ±90°? Нет, это ошибка, так как величина угла θ явно зависит от значения β. Чем больше параметр β, тем сильнее вектор равенства волн λ' = λ отклоняется влево от угла θ = 90° в сторону угла θ = 180°. Количественно это отклонение отображается таблицей 1.

Таблица 1
Скорости β и углы θ, сохраняющие
условие равенства длин волн λ ' = λ.

β 0,0001 0,001 0,01 0,1 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 2,2

θ 90°,003 90°,03 90°,3 92°,9 95°,7 101°,5 107°,5 113°,6 120°,0 126°,9 134°,4 143°,1 154°,1 180°,0   —

Принято считать, что в зависимости от угла θ длина волны λ ' от движущегося источника определяется традиционной формулой:

λ ' = λ (1 – β cos θ),           (1)

где параметр β = v / c     часто называют числом Маха ;
v — скорость источника колебаний, c — скорость звука.

Однако выражение (1) справедливо только для плоских волн. Его использование для круговых волн порождает кривую, которая называется кардиоидой. Уравнение для круговых волн выглядит иначе, а именно:

λ ' = λ [(1 – β² sin² θ) ^½ – β cos θ],           (2)

При малых значениях параметра β кардиоида не слишком заметно отличается от окружности, поэтому в расчетах допустимо использовать приближенную формулу (1). Но при значительной величине этого параметра, например при β = 2/3, указанные отличия становятся заметными, что видно на диаграмме 2, и нужно уже воспользоваться точной формулой Доплера для круговых (сферических) волн (2).

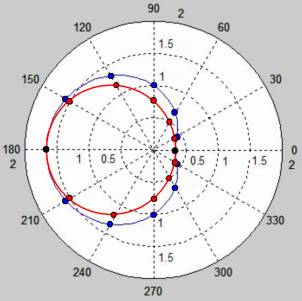Диаграмма 2. Графики волновых фронтов для β = 2/3 и λ = 1, вычерченные в полярных координатах, как наиболее подходящих, согласно традиционному уравнению (1), которое порождает кардиоиду, и уравнению окружности (2) (числовые значения приведены в таблице 2).

Таблица 2
Числовые значения наблюдаемой длины волны λ ' в зависимости от угла θ, рассчитанные по формуле кардиоиды (1) и по формуле окружности (2), когда λ = 1 и β = 2/3 .

Углы наб-ния θ = 0° θ = 30° θ = 60° θ = 90° θ = 120° θ = 150° θ = 180°

Кардиоида λ' = 0.3333 λ' = 0.4226 λ' = 0.6667 λ' = 1.0000 λ' = 1.3333 λ' = 1.5774 λ' = 1.6667

Окружность λ' = 0.3333 λ' = 0.3655 λ' = 0.4832 λ' = 0.7454 λ' = 1.1498 λ' = 1.5202 λ' = 1.6667

Уравнение (2) адекватным образом описывает расходящиеся круговые волны, изображенные на диаграмме 1. Когда угол наблюдения θ = 90°, то для окружности имеем:

λ ' = λ ( 1 – β ² ) ^½ ;     при λ = 1 и β = 2/3 ,     λ ' = 0.7454 .           (3)

Выражение (3) отображает поперечное сокращение длины волны. Традиционное выражение (1) при θ = 90° дает значение, равное λ' = λ = 1, что противоречит реальности. Об этом и многом другом более подробно рассказывается в следующих разделах:

• Введение в акустику. Природа звука и ультразвука
• Введение в конструктивную физику
• О формуле, описывающей классический эффект Доплера
• Ошибочность релятивистской формулы Доплера
• Квантовая теория Доплер-эффекта
• Эксперимент Майкельсона – Морли
• Лекция 4. Эффект Доплера
• Часто задаваемые вопросы по эффекту Доплера
• Идиотский расчет эффекта Доплера
• Использование в медицине поперечного эффекта Доплера для ультразвуковой диагностики сердечно-сосудистой системы
• Эффект сдвига воспринимаемой длины волны в красную область
• Моделирование волновых процессов. Эффект Доплера

Непонимание этого простейшего волнового явления привело Эйнштейна и других релятивистов к математическому формализму, который не имеет ничего общего с реальной физикой. Было изобретено пространство четырех измерений, которое не существует не только в материальной действительности, но и в абстрактной математике.

Далее, читатель продолжал:

Олег, Вы не ответили на мои вопросы, сказав: «Ваши расчеты кажутся мне нелепыми, запутывающими суть дела, а вопросы тупиковыми». Но есть пословица: «Правильно заданный вопрос — это уже половина ответа». Вторую половину ответа я получил, рассмотрев Вашу Диаграмму 1. Теперь мне ясно, что такое Ваша величина λ' и каков ее физический смысл. И тем самым ясна и Ваша фундаментальная ошибка .

Когда я прочитал Вашу фразу «Мне абсолютно чужд тот путь, который Вы проделали, пытаясь усвоить изложенный мной материал», мои глаза от удивления округлились, и я первые минуты даже не знал, что и думать. Я сейчас уже не помню, давали ли нам динамику волновых фронтов на школьных уроках по физике, но что мы это изучали в лагере физматов летом 1964 года — это уж совершенно точно. Это был двухмесячный летний лагерь для победителей районных олимпиад по физике и математике со всей Латвии — в мои последние школьные каникулы перед выпускным классом нас фактически готовили к поступлению на физмат, и в пустующих от студентов аудиториях Латвийского Государственного Университета группа преподавателей Университета провела с нами такой своеобразный ускоренный курс по всем основным дисциплинам физики и математики. Я уже школьником мог на основе анализа динамки волновых фронтов рассчитать и эффект Доплера, и интерференцию, и дифракцию волн... (Фактически в то время я это мог сделать даже лучше, чем сейчас, потому что свежее была в голове и тригонометрия, и всё прочее, а с тех пор в общем-то ничего и не добавилось: на физмат я так и не пошел, физикой больше не занимался, если не считать обычного курса физики для инженеров, который в сущности не дал ничего нового по сравнению с Лагерем). Но с тех школьных лет для меня было само собой разумеющимся всякие рассуждения о волнах начинать с анализа динамики волновых фронтов. И когда Вы говорите «Мне абсолютно чужд тот путь...», то мне остается только развести руками и добавить: «Вот это и привело Вас к тотальному заблуждению». Если бы Вы с самого начала занялись бы такими расчетами, какие здесь проделываю я, то не попали бы в столь неудобное положение, в каком сейчас оказываетесь...

Я теперь понимаю, что когда Вы писали свое: «всем формалистам-феноменалистам, лишенным воображения, настоятельно рекомендуется с помощью циркуля и линейки вычертить рисунок с движущимся источником. Если они возьмут λ = 30 мм и β₂ = 2/3, то при θ₂ = ± 90° получат λ' = 22,4 мм», то имели в виду измерения по рисунку типа Диаграммы 1. Конечно, любой человек, прошедший хотя бы такую школу физики, как я, при этих Ваших словах сразу подумал об анализе реальной динамики волновых фронтов типа моих Рис.1 и Рис.2.

Хорошо, взглянем на Диаграмму 1. Что же она нам говорит? Надеюсь, там изображены волны в какой-то один определенный момент времени? (А не каждая волна в свой момент времени?). Если в один момент времени, то это нечто похожее на фотоснимок с космоса (со спутника) поверхности океана из моих примеров.

Далее Вы на этом фотоснимке чертите прямые линии (векторы) от самолета в разные направления, измеряете длины волн λ' по этим линиям, и ищете то направление, в котором λ' совпадет с λ. При этом Вы видите, что по направлениям ± 90° будет λ' меньше, чем λ, и ЭТО Вы называете «поперечным эффектом Доплера».

Я как бывший школьник физмат-лагеря моментально могу сказать Вам три вещи:

1) То λ', которое измеряете Вы, это НЕ ТО λ', которое измеряет Лоренц и вообще «официальная физика». Вы, конечно, можете измерять свою λ', и строить развитую теорию этой величины со всякими там кардиоидами и т.д., но бессмысленно при этом утверждать, что все те, которые измеряют другую λ', ничего не смыслят в науке, сплошь ошибаются и т.п. Вашей λ', измеренной на космическом фотоснимке по той или иной линии, физика просто не интересуется, потому что эта величина ни на что не влияет. Для физики важна та λ', которая связана с частотойприбытия волн в ту или иную точку. Именно эта частота создает тон звука, цвет света и т.д. А эта частота измеряется не по «космическому снимку», а по времени прибытия волны в данную точку.

2) Например, по направлениям ± 90° Вашей Диаграммы 1 действительно будет (Ваше) λ' меньше, чем λ, но по этой линии фронты волн будут «ползти» медленнее, чем по радиусам, в результате чего частота прибытия волн окажется такой, что если по этой частотевычислить λ' (ту, которая не Ваша), то она будет неограниченно приближаться к λ по мере удаления от источника. Именно этот факт и имеется в виду, когда «официальная наука» утверждает, что «в классической физике не существует поперечного эффекта Доплера». Вы, разумеется, можете называть «поперечным эффектом Доплера» то явление, которое Вы им называете (факт, что на «космическом фотоснимке» по направлениям ± 90° будет λ' меньше, чем λ), но разумный человек должен понимать, что в таком случае это два разных эффекта.

3) Тот узор волн, который создается на чертимых Вами прямых, он моментальный, в следующий момент времени на них будет уже другой узор; то, что Вы измеряете и рассчитываете, это мираж одного момента.

2012.10.24 среда

Рассмотрим наш пример (β₂ = 2/3) в виде, наиболее близком к Вашей Диаграмме 1. Возьмем тот же Рис.2 (когда t = 15 ев ), только отобразим не последние 8 волн, как на Рис.2, а все 15, существующие к этому моменту; чтобы они все «влезли» в рисунок, уменьшим масштаб в 2 раза (Рис.4).

Вы не изучаете, что увидит наблюдатель, находящийся в конкретном месте, когда мимо него движется источник волн; вместо этого Вы проводите от источника волн различные прямые и изучаете, какие на этих прямых будут расстояния между волнами. На Рис.4 показаны две из Ваших прямых в момент t = 15 ев: оранжевым цветом прямая P (θ = –90°) и синим цветом прямая Q (θ = –110°, направление, в котором по Вашим словам будет λ' = λ = 30). Для следующего момента времени t = 16 ев Вы будете изучать уже другие прямые (исходящие от точки x = 320 на курсе самолета), и поэтому никогда не прослеживаете ситуацию до конца.

Ваша оранжевая прямая P была бы меридианом наблюдателя из рисунков 1 и 2, если бы Наблюдатель стоял бы на месте, оставался на одной конкретной прямой, но у Вас он в момент t = 15 находится на прямой x = 300, а в момент t = 16 уже на прямой x = 320 (и в обоих случаях с неизвестной y-координатой).

Для рисунка 4 можно рассчитать действительные λ' (как Вы ее определяете), то есть расстояния между волнами по оранжевой и по синей линии. Уравнения фронтов волн имеют общий вид

(x – 20t_i)² + (y – 200)² = (30(15 – t_i))²,

где t_i – время i-того взрыва. То есть, уравнения отдельно для каждого круга (таблица 13):

Таблица 13

Ц-0:     x + (y – 200)² = 450²
Ц-20:     (x – 20)² + (y – 200)² = 420²
Ц-40:     (x – 40)² + (y – 200)² = 390²
Ц-60:     (x – 60)² + (y – 200)² = 360²
Ц-80:     (x – 80)² + (y – 200)² = 330²
Ц-100:     (x – 100)² + (y – 200)² = 300²
Ц-120:     (x – 120)² + (y – 200)² = 270²
Ц-140:     (x – 140)² + (y – 200)² = 240²
Ц-160:     (x – 160)² + (y – 200)² = 210²
Ц-180:     (x – 180)² + (y – 200)² = 180²
Ц-200:     (x – 200)² + (y – 200)² = 150²
Ц-220:     (x – 220)² + (y – 200)² = 120²
Ц-240:     (x – 240)² + (y – 200)² = 90²
Ц-260:     (x – 260)² + (y – 200)² = 60²
Ц-280:     (x – 280)² + (y – 200)² = 30²

Уравнение синей прямой Q: y = tan 70° (x – 300) + 200, оранжевой прямой P: x = 300.

Нажмите для увеличения

Рис. 4. Взрывные волны в момент t = 15 ев после начала отсчета

Отсюда можно найти точки пересечения обеих прямых с каждым кругом волн, а потом рассчитать расстояние (λ') между волнами по данной прямой. На прямой P это можно сделать и без решения уравнений, просто по теореме Пифагора.

Посчитаем пути, пройденные волнами по прямой P (таблица 14):

Таблица 14

s₀ = √(450² – 300²) = √112500 = 335,41019662496845446137605030969 ед
s₂₀ = √(420² – 280²) = √98000 = 313,04951684997055749728431362238 ед
s₄₀ = √(390² – 260²) = √84500 = 290,68883707497266053319257693507 ед
s₆₀ = √(360² – 240²) = √72000 = 268,32815729997476356910084024775 ед
s₈₀ = √(330² – 220²) = √60500 = 245,96747752497686660500910356044 ед
s₁₀₀ = √(300² – 200²) = √50000 = 223,60679774997896964091736687313 ед
s₁₂₀ = √(270² – 180²) = √40500 = 201,24611797498107267682563018581 ед
s₁₄₀ = √(240² – 160²) = √32000 = 178,8854381999831757127338934985 ед
s₁₆₀ = √(210² – 140²) = √24500 = 156,52475842498527874864215681119 ед
s₁₈₀ = √(180² – 120²) = √18000 = 134,16407864998738178455042012388 ед
s₂₀₀ = √(150² – 100²) = √12500 = 111,80339887498948482045868343656 ед
s₂₂₀ = √(120² – 80²) = √8000 = 89,442719099991587856366946749251 ед
s₂₄₀ = √(90² – 60²) = √4500 = 67,082039324993690892275210061938 ед
s₂₆₀ = √(60² – 40²) = √2000 = 44,721359549995793928183473374626 ед
s₂₈₀ = √(30² – 20²) = √500 = 22,360679774997896964091736687313 ед

Посчитаем λ' (Вашу λ') на прямой P как разность пройденных волнами путей (таблица 15):

Таблица 15

λ'_0–20 = 22,3606797749978969640917366873 ед
λ'_20–40 = 22,3606797749978969640917366873 ед
λ'_40–60 = 22,3606797749978969640917366873 ед
λ'_60–80 = 22,3606797749978969640917366873 ед
λ'_80–100 = 22,3606797749978969640917366873 ед
λ'_100–120 = 22,3606797749978969640917366873 ед
λ'_120–140 = 22,3606797749978969640917366873 ед
λ'_140–160 = 22,3606797749978969640917366874 ед
λ'_160–180 = 22,3606797749978969640917366873 ед
λ'_180–200 = 22,3606797749978969640917366873 ед
λ'_200–220 = 22,36067977499789696409173668725 ед
λ'_220–240 = 22,36067977499789696409173668732 ед
λ'_240–260 = 22,36067977499789696409173668731 ед
λ'_260–280 = 22,36067977499789696409173668731 ед
λ'_280–300 = 22,360679774997896964091736687313 ед

Вот она — Ваша величина λ' = 22,4 мм! Если я до сих пор еще сомневался, правильно ли я Вас понимаю и действительно ли Вы вычисляете именно ЭТУ величину, то теперь все сомнения отпали. Вот он — физический смысл Вашей λ'!

2012.10.25 четверг

Итак, Олег, оказывается, Вы изучаете зыбь на поверхности океана, измеряете расстояния на этой зыби, и изменения этих расстояний называете «эффектом Доплера». Но весь остальной мир эффектом Доплера называет изменения частоты прихода волн к той или иной точке.

Вот мы с Вами обнаружили λ' = 22,3606797749978969640917366873 ед на прямой P в момент времени t = 15 ев после начала отсчета. Этой длине волны при с = 30 ед/ев соответствует частота прихода волн каждые 0,74535599249992989880305788957667 ев. Где на прямой P та точка, в которую волны будут приходить с такими интервалами времени?

Нет такой точки.

Возьмем, например, на прямой P точку y = 335,41019662496845446137605030969, в которой волна Ц-0 находится в момент, изображенный на Рис.4. Посчитаем, в какие моменты в эту точку придут остальные волны. Квадрат этой координаты был 112500, поэтому расстояния до центров волн таковы (таблица 16):

Таблица 16

d₀ = √(112500 + 300²) = 450 ед
d₂₀ = √(112500 + 280²) = 436,92104549906954556392401365173 ед
d₄₀ = √(112500 + 260²) = 424,38190347845889268642669714556 ед
d₆₀ = √(112500 + 240²) = 412,43181254602560059292424743552 ед
d₈₀ = √(112500 + 220²) = 401,12342240263158185498303972506 ед
d₁₀₀ = √(112500 + 200²) = 390,51248379533271970648613678796 ед
d₁₂₀ = √(112500 + 180²) = 380,65732621348561140581318238268 ед
d₁₄₀ = √(112500 + 160²) = 371,61808352124093047472597343688 ед
d₁₆₀ = √(112500 + 140²) = 363,45563690772495707844162072223 ед
d₁₈₀ = √(112500 + 120²) = 356,23026261113751704018752801237 ед
d₂₀₀ = √(112500 + 100²) = 350 ед
d₂₂₀ = √(112500 + 80²) = 344,81879299133334794766375906635 ед
d₂₄₀ = √(112500 + 60²) = 340,73450074801641665354027903954 ед
d₂₆₀ = √(112500 + 40²) = 337,78691508109072992573482830161 ед
d₂₈₀ = √(112500 + 20²) = 336,00595232822885216668099469462 ед
d₂₈₀ = √(112500 + 0²) = 335,41019662496845446137605030969 ед

Так как скорость волны с = 30 ед/ев, а каждый следующий взрыв происходит 1 ев после предыдущего, то волны достигнут нашу точку в такие моменты после начала отсчета времени (таблица 17):

Таблица 17

t₀ = 0 + d₀/c = 15 ев
t₂₀ = 1 + d₂₀/c = 15,564034849968984852130800455057 ев
t₄₀ = 2 + d₄₀/c = 16,146063449281963089547556571517 ев
t₆₀ = 3 + d₆₀/c = 16,747727084867520019764141581183 ев
t₈₀ = 4 + d₈₀/c = 17,370780746754386061832767990833 ев
t₁₀₀ = 5 + d₁₀₀/c = 18,01708279317775732354953789293 ев
t₁₂₀ = 6 + d₁₂₀/c = 18,688577540449520380193772746087 ев
t₁₄₀ = 7 + d₁₄₀/c = 19,38726945070803101582419911456 ев
t₁₆₀ = 8 + d₁₆₀/c = 20,115187896924165235948054024073 ев
t₁₈₀ = 9 + d₁₈₀/c = 20,87434208703791723467291760041 ев
t₂₀₀ = 10 + d₂₀₀/c = 21,666666666666666666666666666667 ев
t₂₂₀ = 11 + d₂₂₀/c = 22,49395976637777826492212530221 ев
t₂₄₀ = 12 + d₂₄₀/c = 23,357816691600547221784675967983 ев
t₂₆₀ = 13 + d₂₆₀/c = 24,259563836036357664191160943387 ев
t₂₈₀ = 14 + d₂₈₀/c = 25,20019841094096173888936648982 ев
t₃₀₀ = 15 + d₃₀₀/c = 26,180339887498948482045868343653 ев

Таким образом, вместо полагающегося для Вашего постоянного λ' ≈ 22,36 также постоянного интервала t' ≈ 0,745 мы на самом деле имеем такие меняющиеся интервалы между волнами в выбранной нами точке на прямой P (таблица 18):

Таблица 18

t'_0–20 = 0,564034849968984852130800455057 ев
t'_20–40 = 0,58202859931297823741675611646 ев
t'_40–60 = 0,60166363558555693021658500967 ев
t'_60–80 = 0,62305366188686604206862640965 ев
t'_80–100 = 0,6463020464233712617167699021 ев
t'_100–120 = 0,67149474727176305664423485315 ев
t'_120–140 = 0,69869191025851063563042636848 ев
t'_140–160 = 0,72791844621613422012385490951 ев
t'_160–180 = 0,75915419011375199872486357634 ев
t'_180–200 = 0,79232457962874943199374906625 ев
t'_200–220 = 0,82729309971111159825545863555 ев
t'_220–240 = 0,86385692522276895686255066577 ев
t'_240–260 = 0,9017471444358104424064849754 ев
t'_260–280 = 0,94063457490460407469820554644 ев
t'_280–300 = 0,98014147655798674315650185383 ев

Измеряемая Вами зыбь существовала одно мгновение (t = 15 ев), а потом на прямой P всё изменилось, и фактическая динамика волн на ее точках была совсем другой. Интервалы времени, через которые волны приходят в выбранную нами точку прямой P и которые показаны в таблице 18, — это фактические характеристики эффекта Доплера для этой точки, именно они изучаются всеми остальными людьми, кроме Вас, под названием «эффект Доплера», и очевидно, что это нечто другое, нежели изучаемый Вами предмет.

Длина волны λ' (та, которая не Ваша) здесь не очень четко определена; она не может быть прямо измерена, а только вычислена как величина, обратная частоте прихода волн. (Поэтому при эффекте Доплера и говорят в основном об изменении частоты, а не о длине волны).

Меня вообще это место в Ваших сочинениях заинтересовало не само по себе (эффект Доплера мне представлялся ясным со школы), а потому что Вы утверждали, будто в «официальной теории» эффекта Доплера существуют какие-то неточности, исправление которых сводит на нет теорию относительности. Именно в этом ракурсе мне и захотелось разобраться. Вот, и разобрался, и теперь мне ясно, что это мираж: данный аргумент против ТО перечеркнут. Это еще не доказывает ТО, остаются другие аргументы, но с данным вопросом всё ясно.

Меня только удивляет одно: неужели Вам за те четверть века, которые Вы преподносили людям свои идеи об «эффекте Доплера», никто так и не объяснил то, что только что сказал я? Или объясняли, но Вы не хотели слушать?

Впрочем, это не так уж важно. Важно, что мне теперь ясно, что мне думать по данному вопросу и как относиться к данному аргументу против ТО.

Подпись, 25 октября 2012 года

*
*   *


Мой ответ на это победное послание:

Здравствуйте, ***

Нужно рассуждать либо только о длине волны, либо только о частоте. В противном случае, Вы допускаете ошибку следующего типа.

Известно, что скорость звука в атмосфере Земли зависит либо от ее температуры, либо от ее давления (плотности) воздуха. То есть, нужно исходить из чего-то одного. Принято строить диаграммы изменения скорости звука только от температуры воздуха. Если учитывать еще и влияние атмосферного давления, то будет допущена ошибка, поскольку одну и ту же физическую причину изменения скорости звука посчитаете дважды, а именно: через два однозначно связанных параметра. Частота и длина волны – два жестко связанных параметра колебательного процесса. Учитывая изменение длины волны, а затем изменение частоты (периода) колебаний, Вы взаимно компенсируете действие обоих этих характеристик. В результате у Вас получилась абсурдная таблица 15.

Итак, мы имеем диаграмму 1, показывающую моментальный снимок волн от движущегося источника колебаний. Про частоту забудем. Никакого наблюдателя тоже приплетать сюда не надо. Этот рудимент передался, видимо, по наследству от субъективистской теории относительности. Снимок расходящихся волн можно сфотографировать сверху с самолета и при его анализе положение наблюдателя может быть любым, т.е. оно не играет никакой роли. Затем задаемся вопросом. Где лежит то направление, на котором λ = λ'? Обнаруживаем, что это направление находится несколько в стороне от прямого угла и лежит под углом 110 градусов. Если скорость источника увеличить, то будет увеличиваться и угол (табл. 1). Отсюда вывод: длина волны λ' должна явным образом зависеть от скорости источника (β). В традиционную формулу (1) β не входит, значит, формула не отражает реального положения дел.

Далее наше внимание переключается на формулу (2). Строим диаграмму 2, на которой продемонстрированы два волновых фронта: от формулы (1) и формулы (2). Видим, что формула (2) порождает круги, а формула (1) – кардиоиду, т.е. она дает явную ошибку. Поскольку диаграмма 2 отражает зависимость длины волны от углового параметра, то легко усматриваем, что красная кривая при угле 90 градусов дает λ = 1 > 0.7454 = λ', т.е. длина волны сократилась. Это при скорости β = 2/3. Чем больше скорость, тем меньше и штрихованная длина волны. То есть, отмеченная ранее зависимость имеет место быть. А вот формула (1) при любой скорости будет давать одно и то же равенство λ = λ' = 1, что не соответствует реальному эффекту Доплера. Кроме того, формула (2) работает и при скоростях движения источника колебаний больше скорости звука (β > 1). Формула (1) для этого случая не годится и у нас нет никакой формулы расчета длины волны для этого случая.

Всего доброго, Олег.

Реакция на это письмо от моего читателя сайта не последовала