Неоклассическая физика

Константин Павлович Агафонов — человек богатого практического опыта и глубоких, разносторонних знаний, инженер высшей квалификации. Родился в Москве в 1934 году. Окончил осковский автомеханический (1957) и Московский энергетический (1966) институты, приобретя в них квалификации инженера-механика и инженера-электрика соответственно. Длительное время работал конструктором в космической (фирма В. П. Бармина) и авиационной (фирмы А. Н. Туполева и В. М. Мясищева) отраслях, а с середины 70-х переключился на поисковые разработки в отрасли тракторного и сельскохозяйственного машиностроения (НПО «НАТИ»). С этого момента начинается его серьёзная научная деятельность, сопровождаемая периодическими убликациями работ (свыше 10) в отраслевых журналах и закончившаяся разработкой стройной теории трения и её приложений.

Работа в должности патентного эксперта отдела энергетики "Федерального института промышленной собственности" (ФИПС) вынудила автора серьёзно заняться физикой, а накопленный к этому моменту богатый опыт и универсальные знания способствовали поиску объективной физической истины в спорах с многочисленными «подкованными» изобретателями новейших конструкций вечных двигателей, летающих тарелок, машин времени и другой экзотики, рожденной современной математической или виртуальной физикой. Результатом стали ведомственные издания шести нетрадиционных брошюр автора по физике, объединённых в предлагаемую здесь современную неоклассическую концепцию.

Персональный сайт К.П. Агафонова: http://neophysics.narod.ru/Index.htm,
и его e-mail: agafonovkp@yandex.ru. Данный материал представил О.Е. Акимов.

Физика реального мира

К.П. Агафонов
(в сокращенном варианте)

Введение

Настоящие очерки представляют собой краткое изложение книги автора "Физика реального мира" (Москва, 2003, 132 с.), посвящённой разработке новой физической (неоклассической) концепции. В книге даётся доступное, последовательное и математически строгое построение основных разделов современной теоретической физики с единых позиций: на базе реальной модели деформирования сплошной материальной среды, приводящей на микроскопическом уровне к универсальному обобщённому уравнению динамики Ньютона-Лоренца. Уравнение включает в себя три силы, характеризующие поведение материальной частицы при отсутствии трения: внешнюю движущую силу, силу инерции частицы и силу упругого деформирования частицей собственного физического или силового поля. При этом какие-либо дополнительные гипотезы к построению физической теории не привлекаются принципиально.

Мы исходим здесь из известного творческого принципа великого Ньютона: «Гипотез не измышляю», — который напрямую предостерегает от использования гипотез в сугубо экспериментальной науке — физике. Между тем, именно гипотезы составляют базис как современной «официальной» или академической физики, так и многочисленных альтернативных физических теорий. В таких условиях надёжно «отделить зёрна от плевел» — физическую науку от «лженауки» — не представляется возможным. Об этом свидетельствует, в частности, и непрекращающаяся почти целое столетие полемика по поводу правомерности геометрического представления реального пространства в теории относительности (ТО) Эйнштейна, и недавние дискуссии вокруг современной гипотезы о торсионных полях или полях кручения Г. И. Шипова, породившие страстный призыв академика В. Л. Гинзбурга к научной общественности: «Не проходите мимо!» (УФН №3, 1999 г., с.359). Призыв предстаёт особенно значимым, если принять во внимание, что к реальному трёхмерному физическому миру скандальные поля никакого отношения не имеют. Ибо (цитируем Г. И. Шипова) «изучение свойств торсионных полей … принципиально невозможно без привлечения пространства событий в виде десятимерного многообразия со структурой геометрии Вайценбека».

Надеемся, что предлагаемый нами неоклассический взгляд на проблему принципиально позволяет установить границу между физикой реального мира, как надёжного фундамента для инженерной, изобретательской и другой практической деятельности, и физикой мира гипотетического или виртуального, пригодной разве что для удовлетворения амбициозных потребностей математиков и при написании фантастических романов. К сожалению последняя также активно участвует сегодня в «обосновании» сомнительных инженерных проектов и изобретений, и далеко не всегда при этом преследуются благие цели.

Возможен ли в принципе достаточно объективный критерий оценки реальности наших физических представлений для предпочтительного использования в практической деятельности, в частности, — в виде упомянутого выше "правила Ньютона"? И насколько отвечает этому требованию предлагаемая концепция физики реального мира или физики для инженеров? — Конкретные и по существу замечания и конструктивные предложения на этот счёт будут приняты автором с почтительной благодарностью по адресу: agafonovkp@yandex.ru.

1. Универсальная модель физических взаимодействий

Постановка задачи. Современная физика развивается в двух основных направлениях: изучение фундаментальной структуры материи и унификация взаимодействий, обусловливающих эту структуру, — гравитационного, электромагнитного, сильного (ядерного) и слабого. Обе эти задачи являются составной частью более общей проблемы, которая представляет собой непреходящую программу развития физики: создание единой картины окружающего нас физического мира на базе ограниченного числа достаточно простых и надёжных исходных принципов.

Первым удачным примером объединения различных физических явлений: электрических, магнитных, оптических — принято считать уравнения электродинамики Максвелла. Они были получены с помощью механической аналогии электромагнитных явлений. И подавляющее большинство физиков ХIХ века: Клаузиус, В. Томсон, Гельмгольц, Больцман, Герц, Лоренц — глубоко верили в возможность механического объяснения немеханических явлений (вспомним слова В. Томсона: «объяснить — это значит построить механическую модель»). Эта вера ещё более утвердилась с широким распространением вариационных принципов механики на описание немеханических явлений и достигла апогея в период создания кинетической теории газа (модель Крёнига) и выявления микроструктуры вещества (модель атома Бора). Затем механические модели в физике уступили место формализованным релятивистским и квантовым представлениям.

Однако многие выдающиеся исследователи эпохи становления современной физики были категорически против радикального изменения физического мировоззрения. «Классическая теория дала нам столько полезного, — предостерегал Планк в письме к А. Ф. Иоффе, — что к ней надо относиться с величайшей осторожностью и охранять её». Последуем здесь этому мудрому призыву.

Вязкоупругопластическая модель материи. Наша задача состоит в том, чтобы описать процессы физического взаимодействия на базе известных фундаментальных законов деформирования реальных тел или сред при сжатии и сдвиге: закона Гука, характеризующего упругое поведение твёрдых тел в пределах малых величин деформаций, и закона Ньютона, описывающего вязкое течение реальных жидкостей. Так как в любых реальных телах оба эти свойства — упругость и вязкость — в большей или меньшей мере проявляются совместно, то для этого в расчётную модель деформирования среды (рис. 1.1) помимо фрикционного элемента (сила П), характеризующего пластическое течение среды при деформировании, частным случаем которого является «чистое» или идеальное внешнее трение, необходимо ввести также упругий (пружинный) и вязкий (гидравлический демпфирующий) элементы и определять силу сопротивления деформированию или равную ей внешнюю силу F как алгебраическую сумму трёх составляющих.

Рис. 1.1.
Вязкоупругопластическая
модель деформирования тел
(АКП-модель)

Закон Гука для твёрдых тел определяет пропорциональность квазиупругих сил относительному изменению объёма тел или относительной их деформации; коэффициент пропорциональности K, называемый модулем упругости или жёсткостью, характеризует напряжённость деформируемого тела. Закон Ньютона для реальных жидкостей определяет пропорциональность вязких сил градиенту скорости частиц в граничном (прилегающем к поверхности деформатора)слое деформируемого тела или среды; коэффициент пропорциональности A называют коэффициентом вязкости ньютоновской жидкости.

Вязкоупругопластическая модель или AKП-система по рис. 1.1 позволяет составить следующие два уравнения деформирования тел — при сжатии и сдвиге соответственно:

F = П + Ku/c – Adu/dy ≈ П + Kβ – au;         (1.1)

F = П + Kv/u – Adv/dy ≈ П + Kγ – aγu.         (1.1а)

Здесь β = u/c и γ = v/u — относительная деформация среды при скрости деформатора u, скорости v течения частиц среды в граничном слое и скорости распространения деформаций (звука) c в среде; приближённое выражение отражает случай линейного распределения скоростей частиц в граничном слое глубиной h; a = A/h — коэффициент объёмной вязкости или просто вязкость граничного слоя. С помощью этих уравнений оказывается возможным решать самые сложные задачи механики сплошных или деформируемых сред, которая оперирует системой бесконечного числа материальных частиц. В частности, в представляемой работе речь идёт о течении реальных жидкостей и газов, формировании ударных волн, законах трения качения и скольжения, процессах износа трущихся поверхностей и др.

Обобщённое уравнение движения частицы. Чтобы перейти к механике отдельной частицы, вязкую составляющую силы трения в уравнении (1.1) представим в следующем виде:

A du/dy = (A dt/dy)(du/dt).

Здесь слева стоит сила, а величина du/dt характеризует ускорение тела. Коэффициент пропорциональности (A dt/dy) назовём инертной массой m вещества, подвергаемого деформированию (перемещению). В результате уравнение деформирования предстанет в виде равенства нулю векторной суммы сил, воздействующих на поток частиц или выделенную частицу:

F + П + [u/c, K] + m du/dt = 0.         (1.2)

При этом необходимо строго отличать реальную внешнюю силу F от сил внутренних — пластической, упругой и вязкой составляющих реакции рассматриваемой системы на воздействие внешней силы, которые и характеризуют физические свойства этой системы.

Слагаемое [u/c, K] в этом уравнении задаёт упругую силу в направлении, перпендикулярном основному движению при скорости u; она обуславливает закрутку потока или частицы при поступательном движении, повсеместно наблюдаемую в реальной жизни. В частных случаях эта сила проявляет себя либо как сила Кориолиса, если речь идёт о нейтральных частицах, либо как магнитная сила, если речь идёт о движении заряда. Полученные уравнения взаимодействия материальных тел и соответствующая им модель рис. 1.1 и используются здесь для построения всех разделов неоклассической физики.

Уточняем законы классической механики. Для нежёстких систем без трения, определяемых условием [u/c, K] = 0 и П = 0, на основании уравнения (1.2) получаем:

F + m du/dt = 0         (1.3)

или

F = – F_ин.         (1.4)

Таким образом, имеем две силы, одна из которых — внешняя — возбуждает ускорение тела

F = m du/dt,         (1.5)

в то время как другая сопротивляется ему. Эту последнюю называют силой инерции и определяют соотношением:

F_ин = – m du/dt,

где m — инертная масса тела. Её направление противоположно направлению вектора ускорения.

При F = 0 из уравнения (1.3) получаем два соотношения:

m du/dt = 0;         u = Const,

которые определяют частный случай движения свободного тела по инерции и утверждают так называемый принцип инерции или первый закон динамики Ньютона: если на тело не действуют внешние силы, то оно покоится или движется равномерно и прямолинейно. При этом из принципа выпадают два практически важных случая движения по инерции: вращение (тяжёлого маховика, например) и вращательно-поступательное движение (качение колеса по плоскости).

Родоначальником принципа инерции справедливо принято считать Галилея. Однако последний полагал, что движением по инерции является равномерное обращение тела по окружности, идея же о прямолинейном движении по инерции была выдвинута позднее, в частности, её придерживался Декарт. И в нашем случае появляется возможность восстановить историческую справедливость в следующей обобщённой формулировке принципа инерции Галилея: движение свободного тела в общем случае включает равномерное вращение и равномерное поступательное перемещение. Эта "новая" формулировка принципа инерции занимает центральное место в предлагаемой нами неоклассической концепции современной физики.

Математическую формулировку принципа для случая вращения тела имеем при подстановке в уравнение (1.2) величин F = 0 и П = 0:

[u/c, K] = – m du/dt.         (1.6)

Величина, стоящая справа, здесь, как и ранее, характеризует силу инерции, которая называется центробежной силой инерции; параметр слева характеризует упругую центростремительную реакцию материала вращающегося твёрдого тела, уравновешивающую указанную центробежную силу инерции.

Подчеркнём принципиально важное: возникновение сил инерции и компенсирующих их сил упругости есть объективное внутреннее свойство реальных тел, проявляемое при всяком воздействии на них внешней силы или вращающего момента в виде ответной реакции на такое воздействие. Этим наш подход отличается от традиционного, в котором проявление этих сил связывают с выбором неинерциальной системы отсчёта: «Центробежные силы, как и всякие силы инерции, существуют лишь в ускоренно движущихся (вращающихся) системах отсчёта и исчезают при переходе к инерциальным системам» [5].

В последнем случае силам инерции часто фактически отказывают в реальности, полагая их фиктивными силами, т.е. обусловленными ускорением системы отсчёта, в которой сила измеряется. Такая точка зрения расходится с инженерной практикой полезного использования сил инерции или борьбы с ними в реальных механизмах. В частности, разрушение быстро вращающегося диска турбины обусловлено именно реальностью возникающих в нём внутренних центробежных сил, и «размещение» такого диска в инерциальной или какой-либо другой системе отсчёта от этих сил и разрушения диск не спасает.

Соотношение (1.5) подтверждает основной закон динамики или второй закон Ньютона, установленный экспериментальным путём и утверждающий: внешняя сила равна произведению массы тела на ускорение, которое она сообщает этому телу. В более общем виде его можно выразить так:

F = d(mu)/dt,

где mu — импульс или количество движения тела. Отсюда устанавливается связь между импульсом силы и импульсом тела:

Fdt = d(mu).

Соотношение (1.4) составляет содержание третьего закона Ньютона и совместно с последним соотношением утверждает равенство внешнего действия и инерционного противодействия.

Для замкнутых систем, описываемых уравнением (1.2), внешняя сила F = 0. Поэтому любая функция, характеризующая систему, производная которой равна или пропорциональна F, является константой. Из этого обстоятельства непосредственно следует формулировка законов сохранения для полной энергии системы (dW/dt = Fu; W = Const), импульса (dp/dt = F; p = Const) и момента импульса (dL/dt = [F, r]; L = Const), на базе которых и соотношений (1.5) и (1.6) здесь строится всё здание классической механики.

2. Физическая природа релятивизма
и структура пространства-времени

Постановка задачи. Рассмотрим круговое движение частицы массой m в поле центральной внешней силы F, обусловленной, например, гравитационной массой M тяжёлого тела (рис. 2.1). Будем непрерывно уменьшать силу (тело М излучает массу), заставляя частицу удаляться от центра вращения. Очевидно наступит момент, при котором сила F практически исчезнет, а частица, став свободной, продолжит, тем не менее, самовращение в силу наличия у неё первоначального сохраняемого момента импульса. Таким образом, приходим к следующей простой мысли: вращение является не результатом воздействия на материальную частицу центральной внешней силы, а природным свойством её, обусловленным взаимодействием с внешней или окружающей средой: материальным или искривлённым (неевклидовым) пространством, мировым эфиром, физическим вакуумом или, наконец, собственным физическим или силовым полем материальной частицы. Сказанное подтверждается наблюдениями: в природе существует один вид движения массивных тел — вращение, и использование инерциальных систем отсчёта при строгом анализе такого движения (СТО Эйнштейна) недопустимо по определению.

Рис. 2.1.
Движение тела в поле
центральной силы

Чтобы не вводить гипотез об искривлённом (неевклидовом) физическом пространстве, мировом эфире или физическом вакууме, будем исходить из классического определения вакуума как абсолютной пустоты и устоявшейся полевой трактовки физических взаимодействий материальных тел. Тогда следует полагать причиной обнаруженного здесь природного самовращения свободных материальных тел исключительно их взаимодействие с собственным физическим или силовым полем. Это может быть, в частности, собственное магнитное поле, взаимообусловленное природным самовращением частицы. Напомним в связи с этим о широко известном опыте по обратимому магнитомеханическому эффекту, впервые обнаруженному Барретом: вращающаяся инертная масса порождает осесимметричное магнитное поле, превращая эту массу в магнит; и наоборот, при внесении незаряженного тела в магнитное поле оно начинает медленно вращаться.

Таким образом, движение свободной самовращающейся материальной частицы можно уподобить движению электрона в магнитном поле и описать следующим обобщённым уравнением Лоренца:

[u/c, K] + m du/dt = 0.         (2.1)

Оно уже знакомо нам — в виде соотношения (1.6) — и представляет собой математическое выражение принципа инерции Галилея в его первозданном виде.

На основании правил векторной алгебры уравнение (2.1) может быть представлено также в следующей комплексной форме:

[iK, iu/c] + m du/dt = 0,         (2.2)

где i — мнимая единица; умножение на мнимую единицу согласно известному математическому правилу физически означает поворот вектора на угол π/2 в направлении движения. Причём наше уравнение способно выступать, по меньшей мере, в двух ипостасях.

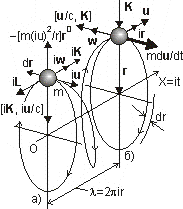
Рис. 2.2.
Модель свободного движения
материальной частицы

«Тёмная материя». Во-первых, оно задаёт сложное вращательно-поступательное (винтовое) движение свободной материальной частицы. Схема сил, действующих на такую частицу, приведена на рис. 2.2. Здесь сечения а и б изображают положение частицы в моменты, сдвинутые на величину шага винтовой траектории. Обратим внимание, что с поступательным движением частицы оказываются связанными мнимая частота iw и мнимое время it, в то время как реальные (действительные) параметры w и t характеризуют вращение.

Решение уравнения обнаруживает так называемую скрытую или мнимую массу im системы частица-поле (аналог «тёмной материи»), обусловленную введением в рассмотрение материальных силовых полей. Количественно связь между массой покоя частицы m₀, релятивистской массой частицы m и скрытой массой системы частица-поле im определяется соотношением

im = m(c/u) = m₀ (c/u)(1 – u²/c²)^–½,         (2.3)

графически представленным на рис. 2.3.

Рис. 2.3.
Зависимость массы частицы-поля
от скорости движения

Графики рис. 2.3 показывают, что диапазон движения материальных тел во Вселенной ограничен двумя космологическими сингулярностями, характеристики которых резко различаются между собой. Область слева определяет холодную Вселенную, которая заполнена конечной массой m₀ вещества и бесконечной мнимой массой силовых полей. Область справа определяет горячую Вселенную «голых» (лишённых силовых полей) "релятивистских" частиц бесконечной массы-энергии, по-видимому, способных инициировать "Большой взрыв" при неупругом столкновении. Эволюция Вселенной в последнем случае сводится к переходу из горячего состояния в холодное (в результате расширения) через энергетический минимум при u/c = 0,6…0,8, в котором, по-видимому, пребывает в настоящее время наша Галактика.

Трёхмерная структура пространства-времени. Из рис. 2.2 видно, что движение частицы по инерции согласно принятой модели осуществляется в реальном трёхмерном пространстве-времени, в отличие от четырёхмерного, виртуального в СТО. Причём, это пространство-время является абсолютным, т.е. характеризуется постоянством скорости распространения деформаций в нём, которое мы определим так:

c = dr/dτ = Const,         (2.4)

где dr — приращение модуля радиуса-вектора r (рис. 2.2, б), τ — период обращения частицы. Это, в свою очередь, означает, что пространство и время как раздельные категории могут и не быть абсолютными: им «разрешено» изменяться таким образом, чтобы отношение характеристик dr и dτ всегда оставалось постоянным, равным скорости света в пустоте.

Используя определение (2.4), при u = dir/dt имеем следующее выражение для относительной деформации силового поля

u/c = dir/dr ≤ 1,0.

В нём переменные легко разделяются:

u dr = c dir.

А интегрирование и несложные преобразования приводят к интересующему нас соотношению для характеристики пространства и времени как самостоятельных (раздельных) категорий:

ir = r (1 – u²/c²)^–½,         (2.5)

iτ = τ (1 – u²/c²)^–½.         (2.6)

Физический смысл полученных соотношений абсолютно прозрачен: для частиц, движущихся с релятивистскими скоростями, расстояния, обусловленные собственными деформируемыми силовыми полями, сокращаются, а время преодоления этих расстояний соответственно уменьшается. На рис. 2.2 этому соответствует уменьшение шага λ = 2πir (сжатие) винтовой траектории движущейся частицы вплоть до нулевых значений при u = c и сокращение периода iτ колебаний.

Соотношения (2.5) и (2.6) являются аналогами кинематических формул СТО, полученных Эйнштейном на базе математических преобразований Лоренца. На них базируется эйнштейновское представление об относительности пространства и времени как раздельных категориях (абсолютно в СТО только четырёхмерное пространство-время), которые противопоставляются ньютоновой модели их абсолютного характера. В нашем случае такое противопоставление оказывается некорректным: признать пространство относительным фактически означает отождествить его с силовым полем конкретного физического объекта. Очевидно, что между силовыми полями как материальными объектами и пространством существует глубокое и принципиальное различие: первые индивидуальны и бесчисленны, второе является общим и единственным. Силовые поля заполняют пространство, но не сводятся к нему. А эффект деформирования времени (2.6), в свою очередь, не даёт оснований для серьёзного обсуждения пресловутого парадокса близнецов: мы живём в абсолютном пространстве-времени, а разделили его на пространство и время, исходя из сугубо практических соображений.

Проблема времени в нашем случае обнаруживает одну особенность. Согласно рис. 2.2 движение физического объекта представляет собой комбинацию абсолютного вращения с действительной частотой w в реальном времени t и прямолинейное относительное движение при частоте iw во времени it, которые являются мнимыми величинами. При оценке времени жизни элементарной частицы или другого материального (биологического) объекта из двух решений, действительного и мнимого, может быть признано реализуемым только одно. Мы полагаем, что это должны быть действительные параметры. Жизнь человека, в частности, измеряется количеством циклов (лет) обращения его вместе с Землёй вокруг Солнца. Отрицательный результат опыта Майкельсона-Морли также объясним абсолютным характером реального времени. Тогда проблемы парадокса близнецов и машин времени, введённое в обиход Лоренцем понятие местного времени лишаются реальной почвы и становятся проблемами мнимыми в буквальном смысле этого слова.

3. Магнитная природа тяготения

Постановка задачи. Современная релятивистская теория тяготения составляет суть общей теории относительности (ОТО) Эйнштейна. Она базируется на принципе локальной эквивалентности гравитационных сил и сил инерции. При этом предполагается, что силы гравитации проявляют себя как реальные физические силы, обусловленные кривизной пространства-времени, которые должны приводить к образованию во Вселенной «чёрных дыр» и излучению характерных гравитационных волн. Однако указанные физические объекты до сих пор достаточно надёжно не зарегистрированы, и здесь мы сталкиваемся с самостоятельной и трудно разрешимой проблемой экспериментальной физики.

Геометрическое решение проблемы тяготения , как показывает опыт развития ТО Эйнштейна, приводит к неразрешимому внутреннему противоречию, обусловленному чуждостью для неё (геометрии) базовых физических понятий — силы, массы и энергии. Оказывается, если описывать свойства реального мира геометрией Евклида, то приходим к понятиям однородного и изотропного пространства-времени, в котором выполняются основные законы реального мира — законы сохранения. При этом, однако, приходится оперировать инерциальными системами отсчёта, которым в реальном мире, как мы видели, нет места. Напротив, неевклидова геометрия искривлённого пространства-времени позволяет оперировать «реальными» неинерциальными системами отсчёта, однако приводит к нарушению законов сохранения импульса и момента импульса в таком мире вследствие неоднородности и неизотропности пространства и закона сохранения энергии вследствие неоднородности времени [2].

По указанным причинам возврат к классическим традициям физики на новом витке эволюционной спирали её развития сегодня нам представляется совершенно неизбежным и необходимым. И речь пойдёт далее об объединении в единое гравитационное поле магнитного поля и поля сил инерции. При этом проблема чёрных дыр с повестки дня снимается, а вместо гравитационных волн теория должна предсказывать традиционные электромагнитные волны как результат изменения во времени магнитных полей взаимодействующих инертных космических масс.

Магнитная природа тяготения. Переходим к второй ипостаси уравнения (2.1). Напомним, что общим решением уравнения гармонических колебаний на комплексной плоскости, заданной неподвижной прямоугольной системой координат X0iY (рис. 3.1), является вращающийся комплексный вектор u, определяемый проекциями x = u Cos wt и iy = iu Sin wt на действительную 0X и мнимую 0iY оси.

Рис. 3.1.
Вращающийся комплексный вектор

Максимальные значения указанных проекций равны u и iu и представляют собой частные решения уравнения колебаний: на рис. 2.2 первому случаю соответствует поступательное движение частицы, второму — вращение; сумма этих решений также является решением уравнения.

Таким образом, наличие в решении задачи мнимого параметра есть свидетельство того, что мы имеем дело с вращающимся комплексным вектором. Очевидно, что такой вектор способен задать на плоскости круговое векторное поле (рис. 3.1), а в пространстве массивного тела — сферическое силовое, в частности, гравитационное поле (рис. 3.2). И в этом случае для описания тяготения нет нужды прибегать к сложному математическому аппарату тензорного исчисления (ОТО Эйнштейна). Гравитационная теория, сформулированная на языке комплексных чисел, радикально упрощается.

Рис. 3.2.
Сферическое поле вращающегося вектора

Вернёмся к рис. 2.2. Видно, что жёсткость K собственного силового поля свободной частицы проявляет себя в виде внутренней силы [iK, iu/c], воздействующей на частицу в радиальном направлении и обеспечивающей тем самым «тяготение» её к центру самовращения. Эта сила обуславливает центростремительное ускорение свободно вращающейся частицы и уравновешена центробежной силой – [miu)²/r]r₀.

Осевая составляющая жёсткости силового поля на рис. 2.2 определяется соотношением:

iK = – iLc/(ir)² = – mciH/(ir)²,         (3.1)

где iH = iL/m = – ru = Const — удельный (на единицу массы) момент импульса iL самовращающейся частицы. Из соотношения (3.1) видно, что она распространяется на прилегающее пространство, убывая по величине обратно пропорционально квадрату расстояния ir от плоскости вращения частицы. Это согласуется с опытами по обратимому магнитомеханическому эффекту: вращающаяся инертная масса порождает осесимметричное магнитное поле, превращая эту массу в магнит; и наоборот, при внесении незаряженного тела в магнитное поле оно начинает медленно вращаться. По-видимому, именно этот эффект и экспериментальный закон Кулона для магнитных сил обнаруживает соотношение (3.1). И в таком случае всякие попытки зарегистрировать какие-то особые гравитационные волны обречены: гипотетические гравитоны, как переносчики гравитационного (фактически магнитного) взаимодействия, должны иметь электромагнитную природу и отличаться от фотонов только длиной волны.

Таким образом, в нашем случае неоклассического подхода к решению задачи приходим к необходимости объединения (по примеру Эйнштейна) магнитного поля, силовые линии которого «искривляют» пространство вблизи массивного тела, и поля сил инерции в единое гравитационное поле. При этом статический закон всемирного тяготения Ньютона получает строгое теоретическое обоснование и может быть представлен в следующих двух формах:

F = – GMm/r²     или     F = GiMim/r²,         (3.2)

где G – постоянная тяготения. Вторая нетрадиционная форма записи закона отражает влияние «тёмной материи» (параметры iM и im) на характер гравитационных взаимодействий, зафиксированное средствами наблюдательной астрономии.

Обращаем внимание читателя на количественное и качественное различия двух форм закона всемирного тяготения (3.2), которые обуславливают различные области их применения. Первая, традиционная форма применима к локальным космическим структурам типа Солнечной системы, в масштабах которой влиянием массы силовых полей можно пренебречь. В этом случае мы имеем дело с отрицательными силами притяжения между космическими телами, обладающими реальной или вещественной массой m или M.

Вторая форма закона утверждает наличие сил отталкивания (антигравитации) в масштабных космических структурах типа галактик или их скоплений, в которых заметную или решающую роль играет мнимая im и iM масса взаимодействующих объектов с преобладанием массы силовых полей над массой вещества. В пользу этого говорят, в частности, наблюдаемые факты разбегания галактик с ускорением вместо "классического" замедления под воздействием сил гравитационного притяжения.

Энергия связи iU тел в планетной системе согласно неоклассической теории определяется соотношением, сходным с известным в ОТО выражением для описания движения частицы вблизи коллапсара:

± iU/mc² = {(1 – r_g /ir)[1 + (iL /mcir)²]}^½;         (3.3)

здесь введён гравитационный радиус тела r_g = 2GM/c². А траектория движения частицы вблизи тяжёлой массы определяется уравнением, также впервые полученным в рамках ОТО:

d²y/dφ² + y = GM/H² + (3GM/c²)y².

Оно позволяет рассчитать известные тонкие эффекты гравитации: смещение перигелия планет в направлении движения, отклонение световых лучей под действием гравитационного поля, гравитационное красное смещение спектральных линий.

Формирование и гибель Солнечной системы. На рис. 3.3а возникновение магнитной силы iK представлено в виде затенённой области поля-магнита, ориентированного вдоль оси самовращения космического тела m₁. Очевидно, что такое тело может объединиться с другим m₂ (рис. 3.3б) или несколькими космическими телами, вращающимися в ту же сторону, и это объединение осуществляется благодаря наличию осевых магнитных сил взаимного притяжения между самовращающимися телами. В результате образуется планетарная (планетная) система с общим магнитным центром самовращения тел в одну и ту же сторону, жёсткость силового поля которой определяется суммарным моментом импульса составляющих систему планет. При этом радиусы r самовращения тел в связанной системе существенно уменьшаются, а их окружные скорости u соответственно возрастают таким образом, чтобы моменты импульса космических тел при переходе от свободного состояния к связанному оставались неизменными.

Рис. 3.3.
Магнитное поле вращающегося тела (а)
и образование планетной системы (б)

Когда в достаточно жёсткое поле образовавшейся планетной системы попадают малые и энергичные (релятивистские) самовращающиеся по малому радиусу свободные частицы m (рис. 3.3б), их скорость может возрасти до предельной около световой или равной скорости света. При этом частицы генерируют излучение, образуя со временем в центре планетной системы излучающее центральное тело М — звезду. Таким образом, мы приходим здесь к альтернативной модели самозарождающейся планетной Солнечной системы: в ней источником жизни «вечного светила» оказываются не ядерные реакции синтеза, а непрерывная подпитка энергией релятивистских космических частиц при наличии мощной, центрально размешённой магнитной ловушки.

Очевидно, что результатом непрерывной подпитки звезды-Солнца релятивистскими частицами является медленное увеличение размеров и массы Солнца, с одной стороны, и соответствующее уменьшение радиусов самовращения планет системы — с другой. Это приводит к последовательному поглощению планет Солнцем, вследствие чего образуемое планетами магнитное поле Солнца непрерывно уменьшается, а с ним уменьшаются и его гравитационные силы. В конечном счёте слабеющие гравитационные силы окажутся не в состоянии сдерживать частицы Солнца вместе и в далёком будущем оно взорвётся.

Энергия связи в планетной системе. Типичные графики отрицательной ветви функции (3.3) качественно представлены на рис. 3.4 для двух значений параметра iL = Const. Для большей наглядности и следуя традициям, графики сдвинуты по оси ординат так, что отсчёт значений энергии связи ведётся не от нулевого уровня, а от величины iE₀ = im₀c² внутренней энергии покоя частицы. В этом случае отрицательные значения функции iU(ir) образуют с осями координат зону потенциальной ямы, а положительные — зону потенциального барьера.

Рис. 3.4.
Энергия связи в планетной системе

Верхняя кривая на рис. 3.4 отвечает условию iL = 0, т.е. характеризует поведение слабо вращающейся частицы m₁ вблизи центрального тела. В этом случае частица не создаёт достаточно сильного собственного магнитного поля и по этой причине не может быть захвачена тяжёлым телом (кривая iU(ir) представляет собой потенциальный барьер высотой iE₀ для частицы). Более того, само тяжёлое тело способно «выплёскивать» в космос низкопотенциальное вещество в виде слабо вращающихся скоплений частиц (солнечный ветер). Нижняя кривая образует с осями координат и потенциальную яму, и потенциальный барьер; она характеризует поведение существенно вращающейся частицы m₂ в планетной системе. Вследствие вращения и взаимодействия магнитных полей частица или тело оказываются захваченными центральным тяжёлым телом с образованием планетной системы.

Графики рис. 3.4 начинаются в точке, отвечающей внутренней энергии iE₀ частицы и радиусу орбиты ir = r_g , задающему минимальное смещение плоскости орбиты частицы от центрального тела, а сходятся к нулевому значению энергии связи при ir, стремящемся к бесконечности. Область ir < r_g является «запрещённой»: при пересечении её границы (горизонт событий в теории «чёрных дыр») частица приобретает световую скорость и обязана превратиться в излучение. Величина «пика» iU_m в сотни и тысячи раз превышает внутреннюю энергию im₀c² для планет Солнечной системы, что свидетельствует о чрезвычайно высокой устойчивости последней.

Рис. 3.5.
Спиральная галактика с "прожекторами"

Как видим, функция iU(ir) не имеет бесконечных значений или сингулярностей, которые Эйнштейн в сердцах назвал проклятьем физики и наличие которых в ОТО связывают с возможностью образования во Вселенной «чёрных дыр» и других сверхплотных космических объектов. Вместо этого неоклассическая теория тяготения предсказывает, в частности, образование в спиральных галактиках центральной области «чистого» излучения в виде "прожекторов", исходящих из ярко светящегося ядра (рис.3.5). Такие объекты представляют собой космическую «печку»: они поглощают относительно высокопотенциальное космическое вещество в направлении оси вращения или магнитной ловушки, формируя "прожекторы", и теряют низкопотенциальное на периферии в спиральных рукавах вращающегося "плоского диска" галактики.

4. Гравитационный характер ядерных сил

Постановка задачи. Метод моделирования, на котором базируется неоклассическая концепция, сохранился сегодня только в ядерной физике. Это обусловлено недостаточным знанием свойств сильных ядерных взаимодействий и сложностью энергетического расчёта систем, состоящих из десятков и сотен сильно взаимодействующих частиц. Наибольшее распространение получили две ядерных модели — капельная (гидродинамическая) и оболочечная. Они описывают различные свойства ядер и процессы в них, и каждая имеет свою область применения. Используемая здесь вязкоупругопластическая модель реальных тел в приложении к капельной ядерной модели продолжает эту традицию и, как мы покажем, кардинально расширяет область её применения.

Наиболее характерными свойствами ядерных сил являются их чрезвычайно малый радиус действия и очень большое значение в пределах этого радиуса. В этом отношении они похожи на гравитационные силы: энергия гравитационной связи (3.3) в планетной системе проявляет себя как сильное взаимодействие (рис. 3.4), распространяющееся на короткие расстояния. И это сходство не случайно.

Ядерные силы между нуклонами лёгкого ядра, например, гелия формируются за счёт уменьшения гравитационных сил составляющих его нуклонов — нейтронов и протонов. Об этом прямо свидетельствует возникновение дефекта масс при ядерном синтезе лёгких ядер. Сущность этого явления заключается в том, что масса ядра гелия оказывается меньше суммы масс составляющих его нуклонов. Это обстоятельство уже само по себе приводит нас к необходимости признания гравитационного характера ядерных взаимодействий.

Энергия связи ядер. Полагаем далее, что отрицательная ветвь функции (3.3) описывает характер изменения энергии связи материальных объектов, испытывающих взаимное притяжение: гравитационные массы, взаимодействие электрона с ядром в атоме. Тогда положительная её ветвь представляет энергию связи объектов, испытывающих взаимное отталкивание, например, взаимодействие протонов в ядре или при столкновении в ускорителе заряженных частиц. На рис. 4.1 эта функция построена для трёх численных значений параметра iL /mcr_g .

Рис. 4.1.
Зависимость iU(ir) для трёх значений параметра iL /mcr_g

Обратимся к конкретному примеру. Для нуклонов в ядре, как известно, энергия связи не превышает одного процента от их внутренней энергии (для протона m_p c² = 938,3 МэВ) и составляет в среднем 7…8 МэВ на один нуклон. На рис. 4.1 такому значению потенциального барьера отвечает средняя кривая для момента импульса iL/mcr_g ≈ 2,0. Гравитационный радиус ядра атома гелия составляет величину r_g ≈ 10^–51 см, а радиус орбиты нуклонов в ядре — 2,0·10^–13 см. Подставляя эти данные в соотношение 2mcr_g = miur для средней кривой рис. 4.1, получаем следующие значения параметров движения нуклонов в ядре: скорость вращения iu ≈ 3·10^–28 см/сек, частота вращения — один оборот за 1,3·10⁸ лет. Таким образом, ядро атома гелия (α-частица) представляет собой практически невращающуюся пространственную структуру, которая характеризуется сравнительно слабым гравитационным взаимодействием нуклонов между собой.

Нижняя кривая на рис. 4.1 отвечает нулевому значению параметра iL/mcr_g , при котором нуклоны в ядре не вращаются, а ядро не имеет чётких границ. Можно показать, что такая характеристика пригодна для описания самопроизвольного (радиоактивного) распада тяжёлых ядер (α-распада).

Разрушение ядра. Дополнительную информацию можно получить при анализе разрушения ядерной материи как сплошной среды, используя расчётную схему рис. 1.1 и приближённое уравнения (1.1а) вязкоупругопластического разрушения (сдвига) реальных тел, полагая процесс разрушения происходящим при постоянной рассеиваемой мощности dW/dt = Const. Это даёт право заменить в уравнении (1.3) скорость скольжения деформатора на отношение мощности к толкающей силе и привести его к квадратному алгебраическому:

F² – (П + Kγ )F + aγ dW/dt = 0;

а в конечном счёте — получить потенциальные характеристики разрушения ядра, представленные на рис. 4.2. Здесь упругие свойства ядерной материи обусловлены взаимным отталкиванием положительных зарядов протонов, а пластические — взаимным гравитационным притяжением нуклонов.

Рис. 4.2.
Потенциальные характеристики вязкопластического (а),
вязкоупругого (б) и вязкоупругопластического (в)
режимов разрушения ядра

Характеристика U₁(x), изображённая на рис. 4.2а сплошной жирной линией, отображает идеальный вязкопластический режим разрушения ядерной материи; в этом случае упругие силы в ядре полностью отсутствуют, что характерно, например, для взаимодействующей пары протон-нейтрон в дейтоне. Зависимость U₁(x) по рис. 4.2б определяет идеальный вязкоупругий режим разрушения ядра, который в чистом виде в природе не встречается; в зависимости от соотношения упругих и пластических свойств ядра острый «пик» характеристики в той или иной мере сглаживается. Наконец кривая U₁(x) по рис. 4.2в задаёт вязкоупругопластический режим разрушения ядра, когда в нём упругие и пластические свойства проявляются в равной мере.

Очевидно, что наибольшую «прочность» или энергию связи ядра обеспечивает зависимость U₁(x) вязкоупругого взаимодействия нуклонов по рис. 4.2б, для которой характерно наличие потенциального барьера или «пика» U_k . Менее прочным, хотя и устойчивым, является ядро с потенциальной ямой по рис. 4.2а. Потенциальная яма по рис. 4.2в не задаёт чётких границ ядра и поэтому не может обеспечить высокой стабильности ядерной материи.

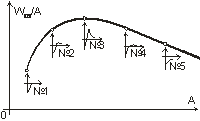
Энергия связи на нуклон. На рис. 4.3 показана идеализированная экспериментальная зависимость энергии связи на нуклон для различных атомных ядер, характеризуемых числом нуклонов А, а под ней изображены соответствующие потенциальные характеристики U₁(x) ядер, пронумерованные от №1 до №5.

Рис. 4.3.
Зависимость средней энергии связи на
нуклон от массового числа ядра

Самому лёгкому ядру — дейтону соответствует идеальная вязкопластическая форма потенциальной ямы (№1) и наименьшая величина энергии связи. По мере увеличения числа нейтронов и протонов в ядре заряд его увеличивается и упругие свойства проявляются всё в большей мере, а энергия связи на нуклон возрастает. На рис. 4.3 этому соответствует потенциальная характеристика №2, представляющая собой некую переходную форму характеристик по рис. 4.2a и рис. 4.2б со сглаженным «пиком». Максимуму энергии связи на нуклон отвечает потенциальная характеристика №3 вязкоупругого взаимодействия нуклонов, имеющая максимальную высоту потенциального барьера; она в наибольшей мере приближается к идеальной характеристике по рис. 4.2б с острым «пиком». По мере дальнейшего увеличения массового числа в ядрах, как известно, количество нейтронов начинает заметно преобладать над количеством протонов и пластические свойства проявляются всё в большей мере. Это приводит сначала к ещё большему сглаживанию «пика» в характеристике U₁(x) (№4), а затем к полному его исчезновению в потенциальной характеристике №5 вязкоупругопластического взаимодействия нуклонов; в последнем случае мы имеем дело с тяжёлыми нестабильными (радиоактивными) ядрами. Таким образом, уменьшение энергии связи на нуклон для лёгких ядер (левая ветвь кривой на рис. 4.3) обусловлено малым суммарным зарядом, а для тяжёлых (правая ветвь) — избытком нейтронов в ядре; и в том и в другом случаях это связано с проявлением пластических свойств ядерной материи.

Представленные на рис. 4.2 графики предлагают ещё три решения — в виде потенциальных характеристик U₂(x), изображённых пунктирными линиями, — которые могут быть использованы для объяснения других свойств ядерной материи. В частности, характеристика вязкопластического взаимодействия U₂(x) по рис. 4.2a пригодна для описания слабого взаимодействия, наблюдаемого при β-распаде ядер и распаде ряда нестабильных элементарных частиц, а характеристика U₂(x) по рис. 4.2б (вязкоупругое взаимодействие) и рис. 4.2, в (вязкоупругопластическое взаимодействие), если только они реализуются в природе, с большой степенью вероятности указывают на безуспешность попыток разделить протон или электрон на составные части — кварки или другие элементы первоматерии.

*
*   *

Опущены два последних подраздела:
5. "Кванты, атомы и уравнения Максвелла" и
6. "Новое учение о теплоте".

Проблема антиматерии

К.П. Агафонов

«Если энергия фотона (реального или виртуального) очень велика,
то он может породить любую пару частица-античастица…»
(Физический энциклопедический словарь, 1984, с. 649)

1. Введение

В современной математической или виртуальной физике кварковая модель сильных взаимодействий и теория электрослабых взаимодействий составляют так называемую Стандартную модель (СМ) фундаментальных частиц и взаимодействий. Она претендует на объяснение всех известных экспериментальных фактов в физике микромира, полученных на ускорителях элементарных частиц. Парадокс, однако, состоит в том, что внутренняя логика самой Стандартной модели и история развития и освоения ускорительной техники указывают на временный характер достигнутого статус-кво: до очередного введения в строй более мощных ускорителей элементарных частиц с их неизбежными сюрпризами. Ибо процесс рождения новых элементарных частиц в ускорителях принципиально ничем не ограничен. И уже сегодня количество элементарных частиц, полученных на ускорителях, в три раза превышает необходимое для построения наблюдаемого материального мира: u- и d-кварки, а также электрон и электронное нейтрино. Помимо этого семейства «существенных» частиц уже открыто ещё два семейства элементарных частиц «несущественных», т. е. не участвующих в процессе создания материи. И поговаривают о предстоящем открытии ещё одного семейства «несущественных» частиц.

«Стандартная модель действительно объясняет многое, — считает один из её создателей Ш. Л. Глешоу [1] — Тем не менее, она пока не является истинной теорией, главным образом потому, что не удовлетворяет наивной вере физика в элегантность и простоту. Она содержит порядка 17 якобы элементарных частиц и точно такое же количество произвольных параметров, типа постоянной тонкой структуры, отношения масс мюона и электрона и различных таинственных углов смешивания (Каббибо, Вайнберга, Кобаяши-Маскавы). Уж конечно, Бог не крутил 17 раз телефонный диск на своём чёрном ящике перед Большим взрывом и его славным сиквелом — человечеством. Наша современная теория незакончена, недостаточна и неэлегантна». Автор делает далее следующий неутешительный вывод: «Физика элементарных частиц…кажется бесконечной дорогой в никуда».

В рамках рассматриваемой здесь неоклассической концепции физики, базирующейся на обобщённом уравнении динамики Лоренца, проблемы элементарных частиц разрешаются кардинальным образом.

2. Характер свободного движения частицы

Обобщённое уравнение динамики Лоренца, помимо ньютоновой силы инерции материальной частицы, учитывает её упругое взаимодействие с собственным силовым или физическим полем, приводящее к движению свободной частицы по винтовой траектории:

[u/c, K] + m du/dt = 0.         (1)

Здесь K — модуль упругости (жёсткость) силового поля частицы, u/c — относительная или релятивистская его деформация, u — скорость частицы, c — скорость распространения деформаций (света) в пустоте, m — масса частицы, du/dt — ускорение движения частицы.

Уравнение (1) можно представить также в следующей комплексной форме:

[iK, iu/c] + m du/dt = 0,         (2)

где умножение на мнимую единицу i физически означает поворот вектора на угол π/2 в направлении движения. Схема сил, действующих на свободную частицу согласно уравнениям (1) и (2), изображена на рис. 1.

Здесь сложное пространственное движение частицы по винтовой траектории представлено в виде комбинации двух простых движений с взаимно перпендикулярными и одинаковыми по модулю векторами скорости: плоского (двухмерного) вращения вокруг оси 0X с окружной скоростью iu = – dr/dt = [r, iω] (см. рис. 1а) при центростремительном ускорении du/dt = [(iu)²/r]r₀, где r₀ — единичный радиус-вектор; и одномерного поступательного движения со скоростью u = idr/dt = [r, ω] (рис. 1б). Сечения а и б изображают положение частицы в моменты, сдвинутые на величину шага винтовой траектории

Из рис. 1а видно, что вращение свободной частицы со скоростью iu приводит к возникновению радиальной вращающейся силы [iK, iu/c], обусловленной упругими свойствами K поля. Эта сила уравновешивает радиальную (центробежную) составляющую силы инерции, связанную с наличием центростремительного ускорения частицы:

[iK, iu/c] = [m (iu)²/r]r₀ или (u/c)K = (m u²/r)r₀.         (3)

А из рис. 1б следует, что поступательное движение частицы порождает циркуляцию силового вектора [u/c, K], который уравновешивает силу инерции частицы в направлении касательной к окружности вращения

(iu/c)K = m du/dt,         (4)

где iu = – rω. Указанные составляющие полной упругой силы и обеспечивают самоподдержание режима свободного винтового движения частицы.

3. Энергия частицы и силового поля

Из уравнения (3) имеем:

E = Kr = pcr₀,         (5)

где p = mu — импульс частицы в направлении поступательной скорости. Физически соотношение (5) определяет полную энергию радиального деформирования силового поля.

Определим теперь энергию деформирования силового поля в направлении поступательного движения частицы. Для этого умножим слагаемые уравнения (4) поступательного движения частицы на скаляр dr = cdt; при подстановке Kdr = dE = mcdu согласно (5) в результате интегрирования получаем:

pc – iW = iE₀.         (6)

Здесь iW = muiu — полная энергия частицы; постоянная интегрирования iE₀ = im₀c²w₀ задаёт внутреннюю или собственную энергию частицы и утверждает эквивалентность массы и энергии. Слагаемые векторы уравнения (6) графически представлены на рис. 2.

Для перехода от векторных величин к скалярным левую и правую части уравнения (6) возведём в квадрат. В результате приходим к основному уравнению релятивистской динамики СТО, устанавливающему соотношение между полной энергией частицы, импульсом её поступательного движения и внутренней энергией

W² = p²c² + (m₀c²)².         (7)

При подстановке величин W² = E²(u/c)² и p²c² = E² оно приводится к виду:

E²(u/c)² – E² = (m₀c²)²     или     i²E²(1 – u²/c²) = (m₀c²)².

Извлекая далее корень квадратный из левой и правой частей последнего уравнения и избавляясь от операторов «плюс-минус» (путём их простого сокращения), приходим к несимметричному — только положительному — решению для полной энергии поступательного движения системы частица-поле iE = m₀c²(1 – u²/c²)^–½, вектор iE которой также представлен на рис. 2. Соотношение указывает на неограниченный рост величины энергии, потребной для разгона частицы до световой скорости, наблюдаемый на практике при исследованиях на ускорителях заряженных частиц. Ясно, что параметры iE и iE₀ не могут быть непосредственно измерены: они представляют собой мнимые величины и характеризуют скрытую энергию частицы-поля.

4. Позитрон Дирака

Решение аналогичной задачи привело П. Дирака в 1930 году к «открытию» частицы с отрицательной энергией (позитрона) и последующей за этим космологической проблеме антиматерии. В его работе [2] читаем: «Вопрос об отрицательных энергиях возник из изучения движения частицы сообразно частному принципу относительности. В нерелятивистской механике энергия W частицы задаётся в функции её скорости u или же количества движения p формулой W = mu²/2 = p²/2m, чему отвечают всегда положительные W; однако в релятивистской механике требуется заменить эти формулы на W² = c²(m²c² + p²), или W = c(m²c² + p²)^½, что позволяет энергии W быть как положительной так и отрицательной».

На этом основании Дирак допускает существование в природе как электронов с положительной энергией, так и «моря» электронов с отрицательной энергией, разделённых энергетическим интервалом 2m₀c² (рис. 3). Все уровни с отрицательной энергией заполнены электронами и на каждом из них находится по одному электрону. Если электрону в состоянии с отрицательной энергией с помощью энергичных гамма-квантов сообщить энергию, превышающую 2m₀c², то он переходит в состояние с положительной энергией и ведёт себя как обычный электрон. При этом в состоянии с отрицательной энергией появляется «дырка», которая ведёт себя как положительная частица с массой электрона — позитрон.

Таким образом согласно Дираку происходит рождение пары электрон-позитрон, которое через короткое время заканчивается их аннигиляцией и излучением гамма-квантов. Причём источником рождаемых названных и других пар в виртуальной физике признаётся материализованный физический вакуум, а в данном конкретном случае некая из его многочисленных разновидностей — электронно-позитронный вакуум или фон электронов в состоянии с отрицательной энергией.

В нашей случае гипотеза физического вакуума как материальной среды оказывается невостребованной, ибо с успехом может быть заменена концепцией силового поля физических объектов. То есть упругой материальной средой, в которой при определённых условиях (релятивистские частицы в сильных полях) возможно временное образование полевых вихрей (элементарных квазичастиц), подобных вихревым макроскопическим образованиям в атмосфере. К такого рода микроскопическим образованиям и относятся, на наш взгляд, все неустойчивые частицы, обильно рождаемые в ускорителях и изучаемые в рамках физики высоких энергий или элементарных частиц. По указанной причине в рамках нашей неоклассической физики проблема антиматерии с повестки дня снимается, а раздел физики высоких энергий оказывается ненужным.

5. Механизм образования пары «частица-античастица»

При движении релятивистской частицы под воздействием внешней силы F в силовом поле большой жёсткости K вместо уравнений (1) или (2) свободного движения имеем:

F – [K, u/c] + m du/dt = 0.

При постоянной скорости движения (стационарный режим) сила сопротивления движению постоянна и равна F. Иными словами, процесс деформирования силового поля происходит при постоянной рассеиваемой мощности dW/dt = Const. Это даёт право заменить в последнем уравнении скорость частицы на отношение мощности к толкающей силе. В результате приходим к квадратному алгебраическому уравнению деформирования силового поля:

F² – KβF + aβdW/dt = 0.         (8)

Здесь введены следующие обозначения: β = u/c — деформации силового поля; m = au/c = aβ — масса деформируемого поля, которую мы полагаем пропорциональной (а — коэффициент пропорциональности) величине деформаций.

Квадратное уравнение (8) имеет два действительных корня

F_1,2 = Kβ/2 ± [K²β²/4 – aβdW/dt]^½,         (9)

графически изображённых на рис. 4 в функции деформации силового поля. Графики определяются комбинацией прямой 1 и гиперболы 2 с горизонтальной осью и асимптотой 3. Величина «пика» или «горба» (называемого в газовой динамике λ-скачком уплотнения) в два раза превышает предельное значение F_пр функции. Функциям F₁(β) отвечают отрицательные значения радикала в соотношении (8) и жирные линии графиков, функциям F₂(β) — положительные значения радикала и пунктирные линии графиков.

Полученный результат позволяет нарисовать условную (плоскую) картину формирования микровихрей силовых полей, которая представлена на рис. 5. Здесь релятивистская микрочастица или гамма-фотон 1 деформируют внешнее силовое поле ускорителя, возбуждая присоединённую ударную волну в виде симметричного λ-скачка уплотнения (толстые тёмные линии). Последний, в свою очередь, формирует за фронтом ударной волны, вращающиеся в противоположные стороны, положительный 2 и отрицательный 3 микровихри, которые в камере Вильсона идентифицируются как частица и античастица. Как и положено любым вихреобразованиям, длительное время существовать они не могут и через некоторое время гибнут, преобразуясь в излучение. Здесь обязана наблюдаться полная аналогия с вихревыми макрообразованиями, ибо материальный мир един и резкая граница между макро- и микромиром принципиально недопустима.

6. Виртуальный фокус-покус

П. Дирак пришёл к понятию отрицательной энергии и античастицы (позитрона), опираясь на релятивистски инвариантное соотношение

W² = c²(m²c² + p²)         (10)

к которому в учебной литературе чаще приходят, используя следующую простую схему.

Принцип наименьшего действия позволяет получить два релятивистских соотношения, определяющих положительные величины энергии и импульса материальной частицы:

W = mc²(1– u²/c²)^–½,         (11)

p = mu(1– u²/c²)^–½.         (12)

Возведём далее каждое из них в квадрат и выразим следующим образом:

W²/c² = m²c²(1– u²/c²)^–1,       p² = m²u²(1– u²/c²)^–1.

Вычитая почленно полученные равенства, имеем:

W²/c² – p² = m²c²,

откуда

W = ± c(p² + m²c²)^½.         (13)

Вот так, с помощью элементарной «математики» частица с положительной энергией (11) обретает своего «двойника» — античастицу с отрицательной энергией в соотношении (13). И можно, используя эту схему, пойти ещё дальше: не привлекая соотношение (12) для импульса, возвести в квадрат непосредственно и только положительную энергию (11) частицы, а затем вычислить корень квадратный из полученной величины. В результате вместо одной частицы получаем дираковскую пару частица-античастица!

Подобного рода «математику», точнее антифизику даже комментировать неприлично. Мы привели её здесь, во-первых, для того, чтобы показать: выводу инвариантного соотношения (10) всегда сопутствует операция возведения слагаемых в квадрат; во-вторых, продемонстрировать неправомерность в этом случае использования обратной операции в виде соотношения (13).

И без всякой математики ясно: серьёзной физики в понятии отрицательной энергии не обнаруживается. Если рождённые физическим вакуумом электрон и позитрон определяют частицы с положительной и отрицательной энергией соответственно, то при их аннигиляции следовало бы ожидать нулевой баланс энергии, т. е. последняя должна была бы вовсе исчезнуть. Ан, нет: вместо этого в процессе аннигиляции выделяется удвоенная положительная энергия в виде двух гамма квантов. И это прямо и недвусмысленно свидетельствует исключительно о положительной энергии обоих частиц. Античастица — это физический нонсенс.

В пользу такого вывода говорит и современная космологическая проблема, связанная с хорошо изученным «обычным» или барионным веществом: «соответствующих античастиц, т. е. антибарионов (антипротонов, антинейтронов), позитронов в природе нет. Точнее, они присутствуют в ничтожных количествах и обязаны вторичным процессам рождения частиц и античастиц при столкновениях частиц высоких энергий, например, в космических лучах или на мощных ускорителях в лаборатории» [3].

---

1. Глешоу Ш. А. Очарование физики. — М.: РХД, 2002, с. 194, 297.
2. Дирак П. А. М. К созданию квантовой теории поля. — М.: Наука, 1990, с. 218.
3. Архангельская И. В., Розенталь И. Л., Чернин А. Д. Космология и физический вакуум.– М.: URSS, 2006, с. 38.