Конструктивная математика

Акимов О.Е.

34. Фракталы и солнечная система

Физик-геометр Ньютон и его «верный слуга» астроном Галлей при описании движения узлов орбиты Луны забыли на время о всемирном законе тяготения, открытый Робертом Гуком (см. Кто открыл основы классической механики), и взяли на вооружение систему Птолемея, в которой существовали эпициклы и деференты. В своих «Математических началах» Ньютон писал: «Наш соотечественник Горрокс первый предположил, что Луна движется по эллипсу вокруг Земли, находящейся в нижнем его фокусе. Галлей поместил центр эллипса на эпицикл, центр которого равномерно обращается вокруг Земли; от движения по эпициклу и происходит вышесказанное неравенства в виде прямого и попятного движения апогея и изменений величины эксцентриситета» [25, с. 582].

Здесь не названо имя Кеплера, который открыл законы эллиптического движение, справедливого в отношении планет солнечной системы. Однако Флемстид, современник Ньютона и Галлея, считал, как само собой разумеющееся, что все тела солнечной системе подчиняются законам Кеплера, которые, в свою очередь, продиктованы всемирным законом тяготения. Ньютон и Галлей не соглашались с ним и говорили, что кометы движутся особым образом, а именно, по прямым. Это означало, что любая комета, появившаяся однажды в небе, никогда больше не возвращается к Солнцу. Флемстит же на основе тщательно проведенных наблюдений и расчетов доказывал им ошибочность такого взгляда. Через много лет они были вынуждены принять позицию Флемстида, но дело представили так, будто только благодаря их наблюдениям за кометами была установлена истина.

Таким образом, в споре с Флемстидом Ньютон и Галлей в отношении комет, фактически, признали действие всемирного закона тяготения, хотя в отношении движения Луны они оба во многом оставались еще на позициях Птолемея. Это отступление от законов физики Нового времени, заложенных Декартом и Гуком, Ньютон и Галлей сделали потому, что динамическая система трех тел Луна — Земля — Солнце (рис. 71) описывается очень сложной механикой, законы которой в общем виде еще до сих пор не найдены. Современные астрономы пользуются приближенными выражениями, которые периодически нужно корректировать, т.е. на основе сегодняшних формул нельзя рассчитать положение Луны на сколь угодно длительное время.

Рис. 71

Всемирный закон тяготения прекрасно ощущал уже Коперник, правда, он не имел о нем никакого количественного представления. Польский астроном понимал, какую роль играет светило при круговом движении планет, однако движение некоторых небесных тел было настолько запутанным, что он просто вынужден был прибегать к птолемеевским эпициклам, с помощью которых производил числовую подгонку под фактические данные астрономических наблюдений. Так что формально-феноменологической подгонкой занимался не только Птолемей, но и Коперник, Ньютон, Галлей, а также многие современные астрономы. Чтобы представить себе, с чем приходится иметь дело в наблюдательной астрономии, расскажем чуть подробнее о характере движения Луны.

На рис. 72 показаны линии смещения узлов орбиты Луны, на рис. 73 — ход изменения склонения Луны за 18,6-летний период, а на рис. 74 — диаграмма, показывающая, как ежемесячное максимальное склонение Луны циклически возрастает по мере приближения к периоду «высокой» Луны (точки соответствуют максимальным склонениям Луны в данный месяц).

Рис. 72

Рис. 73

Рис. 74

Период обращения Луны составляет 27,3 суток; плоскость ее орбиты не совпадает с плоскостью небесного экватора, а к плоскости земной орбиты она наклонена под углом i = 5°, который нисколько не изменился с времен неолита. Поэтому Луна пересекает плоскость эклиптики дважды в месяц. Точки пересечения называются узлами ее орбиты и обозначаются как N₁ и N₂, причем узел N₁ называется восходящим, N₂ — нисходящим. Плоскость лунной орбиты вращается, и узлы совершают полный оборот в течение 18,6 лет. Наклон эклиптики (ε), т.е. угол между небесным экватором и плоскостью орбиты Земли, несколько изменяется; величина наклона эклиптики сейчас составляет 23,5°. При максимальном лунном склонении углы i и ε складываются, что дает величину 29°. Это положение Луны называется высоким; при низкой Луне углы i и ε вычитаются, что дает величину 19°. В результате наблюдатель в течение 18,6-летнего периода может видеть следующую картину. В период высокой Луны, который длится примерно 3 года, наблюдатель каждый месяц видит ее либо слишком высоко (+ i + ε), либо слишком низко (– i – ε) над горизонтом. Затем, через 9 лет, амплитуда ежемесячных ее колебаний постепенно уменьшается, и во время низкой Луны колебания совершаются между двумя крайними значениями: (– i + ε) и (+ i – ε).

Лунные затмения всегда будут происходить в полнолуние, когда Луна находится в узлах N₁ и N₂, т.е. два раза в год с интервалом ровно в 6 месяцев. Поскольку узлы совершают 18,6-летний цикл, время наступления затмения из года в год меняется, но через указанный период времени фазы Луны, а значит, и затмения, повторяются в те же самые дни, хотя есть рассогласование в часах. Три 18,6-летних цикла дают один 56-летний цикл. Не имея удовлетворительной теории движения Луны, астрономы с древнейших времен все же умели предсказывать ее затмение, наступление которого прогнозировалось хотя и не с поминутной точностью, как сейчас, но достаточно определенной, чтобы можно было ожидать затмение диска в течение одной ночи. Предположительно считается, что древние британцы умели предсказывать лунные затмения с помощью древнейших астрономических обсерваторий. Одна из таких обсерваторий хорошо нам известна — это знаменитый Стоунхендж, на территории которого были обнаружены так называемые лунки Обри, число которых равно как раз 56. Рис. 75 поясняет методику, предложенную Хойлом, исследователем этого древнего кромлеха, для предсказания лунных затмений с помощью лунок Обри.

Рис. 75

Хойл предположил, что кольцо с лунками было снабжено четырьмя маркировочными камушками, которые условно называл Солнцем (S), Луной (M), Восходящим узлом (N₁) и Нисходящим узлом (N₂). Чтобы отслеживать лунные затмения, необходимо было маркировочные камушки бросать в соответствующие лунки. При затмении камни S и M должны находиться друг против друга; пусть это будут лунки 10 и 38 (рис. 75), тогда камни N₁ и N₂, должны находиться в лунках 18 и 46, соответственно. Далее, камень S каждые 13 дней перебрасывался на две лунки против часовой стрелки, совершая полный цикл в течение одного года. Камень M каждый день перебрасывался через лунку против часовой стрелки, так что он совершал полный цикл за 28 дней. Камни N₁ и N₂ всегда должны находиться друг против друга на одном диаметре и перемещаться на одну лунку каждые четыре месяца, они совершали полный цикл за 18,6 лет.

Если это было действительно так и Хойл правильно реконструировал ход рассуждений британских астрономов, живших приблизительно за 2-3 тысячи лет до Р.Х., то перед нами один из самых чудных примеров рационально-конструктивного подхода, опирающегося на конкретную модель. В правильности предложенной реконструкции можно сомневаться, однако абсолютно достоверно известно, что с помощью лунок Обри и других ориентиров обсерватории Стоунхендж можно было точно определять дни равноденствия, летнего и зимнего солнцестояния, а главное, прогнозировать восходы и заходы низкой и высокой Луны.

Ньютон попытался рассчитать центр тяжести системы Луна — Земля. В Следствии 4 к Предложению 37 книги III «Начал» он писал: «Так как, на основании астрономических наблюдений, истинный диаметр Луны относится к истинному диаметру Земли, как 100 к 365, то масса Луны относится к массе Земли, как 1 к 39,788». Ньютон ошибся: невозможно по отношению диаметров Луны и Земли правильно найти отношение их масс, так как при этом не учитывается различная плотность вещества Луны и Земли. Земля имеет тяжелое железное ядро, которое когда-то, около 5 млрд. лет назад, в момент формирования планеты, было кометой (железо составляет 35 % от массы Земли); ядро покрывает сравнительно легкая базальтовая мантия. Луна же целиком состоит из базальта; железа она содержит ничтожные проценты. Истинное отношение масс Луны к Земле равно не 1 к 40, а 1 к 80. Эта ошибка привела к ложному определению их общего центра тяжести. В Следствии 6 Ньютон писал: «Расстояние центра Луны от центра Земли относится к расстоянию центра Луны до общего центра тяжести ее и Земли, как 40,788 к 39,788». На самом деле, среднее расстояние между центрами Земли и Луны равно 384 000 км; их общий центр тяжести лежит в 4700 км от центра Земли в сторону Луны; следовательно, указанное Ньютоном отношение должно выглядеть как 38,4 к 37,9, т.е. у Ньютона отношение выражалось числом 1,025, в действительности же оно равно 1,013.

Ньютон даже не пытался определить местонахождение центра тяжести солнечной системы, однако он допустил непростительную ошибку, когда написал: «Центр системы мира находится в покое. Это признается всеми, ибо одни принимают находящимися в этом центре и покоящимися Землю, другие — Солнце» [25, с. 526]. Здесь удивляет разъяснения Ньютона, почему нужно принять центр мира в качестве неподвижной точки. Предложение 9 он сформулировал следующим образом: «Общий центр тяжести Земли, Солнца и всех планет находится в покое». Центр тяжести динамической системы не может находиться в покое, так как перераспределение значительных масс внутри системы, например соединение Юпитера и Сатурна или их оппозиция, неизбежно приведет к изменению местоположения центра тяжести. Часто в своих суждениях о тяготении, лучах света и эфирной среде Ньютон не имел собственной физической модели и руководствовался исключительно формальными постулатами.

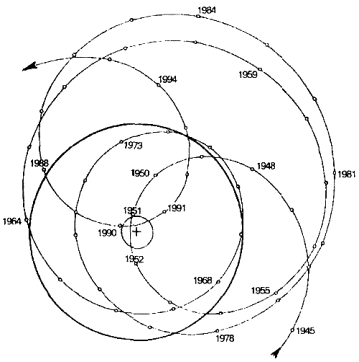
На рис. 76 показано движение центра тяжести солнечной системы относительно геометрического центра Солнца, отмеченного крестиком, в период с 1945 по 1994 гг. Малый круг с крестиком в центре показывает границы солнечного ядра с максимальной плотностью вещества; большой круг является видимой границей солнечного диска. В соответствии с законом сохранения общего вращательного момента системы, переменная конфигурация планет приводит к изменениям вращательного момента светила.

Рис. 76

На рис. 76 мы видим, сколь сложна и нерегулярна траектория центра тяжести, тем не менее, рис. 77 демонстрирует определенную регулярность в отношении динамики отклонения вращательного момента Солнца от среднего значения, сглаженного по 9-летним интервалам за время с 720 по 1070 гг. На диаграмме виден приблизительно 180-летний цикл. Пятипалая регулярность сохранится, если сглаживание произвести по 3-летним интервалам.

Рис. 77

На рис. 78 показана диаграмма, соответствующая этому случаю, только время слежения охватывает период с 1800 по 2000 гг. Здесь уже обнаруживается приблизительно 36-летний цикл. Итак, за хаотическим движением центра тяжести солнечной системы просматриваются вполне регулярные пятипалые периодичности для двух различных статистических видов сглаживания. Подобные процессы получили название фрактальных (о фракталах, читайте в разделе Что такое фрактал курса «Дискретная математика» [4] и далее).

Рис. 78

Не вдаваясь в статистические детали, отметим, что выявленные отклонения углового момента от среднего значения определенным образом коррелирует с 11-летним циклом активности Солнца, а он, в свою очередь, определяется 11-летним периодом обращения самой большой планеты солнечной системы — Юпитера. Используя различную методику сглаживания пульсаций в появлении солнечных пятен, астрофизики помимо основного периода выделили ряд побочных гармоник, в частности, с периодом 7,2 года, 35,8 лет и 178,8 лет; два последних периода совпадают с периодами, продемонстрированными на рис. 77 и рис. 78. Выходит, что механические перемещения центра тяжести солнечной системы напрямую связаны с термоядерными процессами, протекающими в недрах нашего светила.

Между тем, на сегодняшний день существует обширная литература, авторы которой пытаются установить взаимозависимость между активностью Солнца и количеством аварий на транспорте, самочувствием людей, колебаниями рождаемости, биржевыми котировками, социальными катаклизмами, выпадением среднегодовой нормы осадков, изменением каких-то других факторов. На этих полуэмпирических данных паразитирует огромная армия сомнительных «ученых», которые за видимой физической реальностью ощущают, как они говорят, действие неких таинственных космических сил.

Особенно здесь усердствуют астрологи, которые по различным аспектам, т.е. угловым расстояниям между планетами (оппозиция — 180°, тригон — 120°, квадрат — 90°, секстиль — 60°), влияющим на положение центра тяжести солнечной системы, предсказывают судьбы людей и мира. Опровергнуть эти спекуляции порой нелегко, так как динамика всей солнечной системы и события, происходящие на Земле, включая биологические и социально-исторические ритмы, действительно оказываются весьма когерентными явлениями, о чём говорилось в конце подраздела 4.7 «Дискретной математики», который называется Динамика популяций. Эти же проблемы затрагиваются в следующем разделе этой книги.