
Конструктивная математика
Акимов О.Е.
35. Дискретная гравитация и аттракторы
Принято считать, что законы классической механики не диктуются целочисленными параметрами, как это имеет место в квантовой механике, например, для частоты fmn излучения и поглощения (см. раздел 23 и раздел 24). Но оказалось, что это не совсем так, а, точнее, это совсем не так: гравитационные взаимодействия в Солнечной системе подчиняются законам гармонии целых чисел. Искания Кеплера, а до него, пифагорейцев и платоников, не были лишены смысла; в космосе, действительно, звучит «музыка небесных сфер». Дело даже не в том, что периоды орбитального и осевого вращения планет, спутников и астероидов находятся в дробно-рациональных отношениях (об этом мы будем сейчас говорить), а в том, что на движение любого объекта солнечной системы оказывают влияние все остальные объекты. Нельзя говорить о параметрах орбиты одного тела, игнорируя движение другого, даже если последнее находится вдали от первого.
Например, считается, что на так называемое аномальное смещения перигелия Меркурия влияет только мощное поле притяжения Солнца. Вот почему, говорят нам релятивисты, и не наблюдается заметных аномалий для других планет. На самом же деле, «аномалию» первой планеты определяет плотная околосолнечная среда. Высокая плотность вещества солнечного ветра в расчетах релятивистов никогда не принималась.
Кстати, искривление луча света от далеких звезд вблизи затемненного Луной диска Солнца, тоже происходит по этой же причине, так что мы имеем дело не с «гравитационной линзой», о чём без устали твердят релятивисты, а с обычной оптической. Как известно, лучи света от восходящих и заходящих за горизонт звезд, которые видны с Земли, тоже испытывают атмосферную аберрацию, по причине которой мы можем наблюдать некоторое время звезды, фактически скрывшиеся за линией горизонта.
Релятивисты абсолютно не учитывают это вполне земное явления, но зато начинают много фантазировать на счет влияния гравитации на распространение света. Впервые на фальсификацию в этом деле пошел Эддингтон, когда в 1919 году из множества звезд отобрал только те немногие, свет от которых отклонялся в соответствии с эйнштейновской теорией. Потом релятивисты пошли еще дальше и начали рассказывать сказки о существовании черных дыр, косвенное подтверждение которых они сейчас находят чуть ли не каждый день.
Между тем наличие плотной околосолнечной среды и так называемое аномальное движение нисколько не противоречит тому, что параметры орбиты Меркурия, Венеры, Земли и даже Юпитера тесно взаимосвязаны. Между их орбитальными и осевыми периодами имеются четкие дробно-рациональные отношения, которое не только не учитываются релятивистской теорией, но и прямо противоречат ей. Ведь если релятивисты указывают на взаимосвязь орбитальных характеристик Меркурия с полем тяготения Солнца, то в рамках их же теории должно получить объяснение дробно-рациональные отношения орбитальных и осевых крутящихся моментов для Венеры, Земли и Юпитера. Но общая теория относительности на этот счет хранит полное молчание. Поэтому отложим в сторону релятивистские бредни и посмотрим, при каких обстоятельствах заговорили о квантовых свойствах движения небесных тел, кем и когда впервые были обнаружены законы целых чисел, применительно к макрообъектам солнечной системы.
В 1772 г. немецкий астроном Иоганн Боде (1747—1826) опубликовал книгу, где привел любопытное наблюдение, о котором ему рассказал И.Д. Тициус. Последний заметил, что расстояния планет до Солнца (Rn) подчиняется более или менее строгой закономерности, которая носит квантовый характер и выражается формулой:
Rn = (0.4 + 0.3 · 2n) a.e., где n = –∞, 0, 1, 2, 3, 4, 5, 6, 7, 8.
Позднее порождаемые ею числа стали называться рядом Тициуса или законом Боде. В книге Боде «Anleitung zur Kenntniss des gestirnten Himmels» были приведены следующие слова Тициуса: «Обратите внимание на расстояние планет одной от другой, заметьте, что они отдалены одна от другой почти в пропорции их величины. Дайте расстоянию от Солнца до Сатурна 100 частей, тогда Меркурий отстоит от Солнца на 4 такие части, Венера 4 + 3 = 7, Земля 4 + 6 = 10, Марс 4 + 12 = 16. Но, посмотрите, от Марса до Юпитера происходит уклонение от этой точной прогрессии. От Марса следует пространство, равное 4 + 24 = 28 таких частей, а на этом расстоянии нет ни планеты, ни спутника. Неужели Зиждитель мира оставил бы это место пустым? Никогда! Будем уверены, что это пространство принадлежит какому-нибудь не открытому еще спутнику Марса, или допустим, что может быть Юпитер имеет еще несколько спутников, которые еще до сих пор не видны ни в одно стекло. За этим нам неизвестным пространством начинается сфера действия Юпитера, на расстоянии 4 + 48 = 52, и Сатурна, на расстоянии 4 + 96 = 100. Какое поразительное соотношение!»
В табл. 44 дается сравнение чисел, полученных по закону Боде (Rn), с реальными значениями больших полуосей планет (rn), выраженными в астрономических единицах (1 а.е. = 150 млн. км)
Таблица 44
| Меркур | Венера | Земля | Марс | Церера | Юпитер | Сатурн | Уран | Нептун | Плутон | |
| n | –∞ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Rn | 0.4 | 0.7 | 1.0 | 1.6 | 2.8 | 5.2 | 10.0 | 19.6 | 38.8 | 77.2 |
| rn | 0.39 | 0.72 | 1.00 | 1.52 | 2.77 | 5.20 | 9.54 | 19.19 | 30.07 | 39.53 |
После открытия 1781 г. Гершелем седьмой планеты, которую Боде назвал Ураном, стало ясно, что она тоже подчинена этому закону. С этого времени закон Боде стал широко известен и астрономы всего мира кинулись на поиски неизвестной планеты, которая должна была находиться между Марсом и Юпитером. В 1800 г. под руководством Цаха и Шрётера было образовано даже специальное астрономическое общество, ставившее задачу найти предполагаемую планету. Наконец, в самую первую ночь нового столетия, т.е. 1 января 1801 г. поиски планеты увенчались успехом: итальянский астроном Джузеппе Пиацци открыл малую планету, которую он в честь древнеримской богини плодородия назвал Церерой. Бернский астроном Генрих Ольберс в 1802 г. обнаружил вторую малую планету, названную Палладой. Она, как и Церера, имела средний орбитальный радиус, близкий к величине, предсказываемой законом Боде, т.е. 2,8 а.е. Вскоре были открыты еще два астероида — Юнона (Гардинг, 1804) и Веста (Ольберс, 1807) (их размеры на фоне лунного диска показаны на рис. 79). После продолжительной паузы был открыт пятый астероид Астрея (Генке, 1845) и прочие. К 2000 г. известны элементы орбит свыше 65 тыс. астероидов. Подавляющее их число располагается на расстоянии 2,2—3,6 а.е. от светила.
Рис. 79
Таким образом, орбиты астероидов и планет солнечной системы совершенно определенно квантифицированы. Несомненно, эмпирически найденный ряд Тициуса отражает какой-то дискретный закон небесной механики, который, однако, абсолютно не укладывается в ньютонову механику. Маловероятно, чтобы такая высокая степень регулярности в расположении планет была случайной. Здесь существует какая-то система орбитальных запретов и предпочтений: не все энергетические состояния, разрешенные всемирным законом тяготения, могут быть заняты массивными телами.
Дискретная закономерность Тициуса — Боде сильно нарушается Плутоном, что и понятно, поскольку его необходимо причислять уже, собственно, не к планетам, а к одному из многих так называемых транснептуновых объектов. Дело в том, что за пределами восьмой планеты существует второе кольцо из малых космических объектов, из которого время от времени вылетают кометы и движутся по направлению к Солнцу. Когда-то вся Солнечная система представляла собой одно большое кометное облако. Затем, в течение нескольких миллиардов лет шло формирование девяти планет и их спутников. Сегодняшнее состояние Солнечной системы представляет собой устоявшуюся систему пространственно-временных отношений, в которой наблюдаются удивительные закономерности.
Закон Боде можно представить выражением, аналогичным тому, по которому определяется константа Фейгенбаума (см. подраздел 4.9 курса «Дискретная математика» [4, c. 561]):
.
В главе «Фракталы» [4] рассказывалось о квазиаттракторах от рекурсивной функцией ax cos(x) (см. подраздел 4.12), которые возникают при a = 2. Характерной особенностью квазиаттракторных уровней является то, что их величина тоже удовлетворяет данному отношению (рис. 80):

Рис. 80
Аттракторы или квазиаттракторы — это устойчивые образования, которые позволяют объяснить наличие стационарных состояний в бесконечно большом разнообразии возможных состояний. Поскольку динамика вращения небесных тел подчиняется закону ax cos(x) и, как было выяснено на динамике активности Солнца (рис. 77 и 78), в солнечной системе действуют законы рекурсии, то появление квазиаттрактора вроде тех, что показаны на рис. 80, вполне вероятно. Возможно, что у каких-то планетных систем других звезд условия возникновения квазиаттракторов по тем или иным причинам не сложились. Однако это вовсе не значит, что объяснения на основе квазиаттрактора вообще невозможно. Напротив, существование любых стационарных состояний, возникших в динамическом хаосе, только и можно объяснять с помощью теории аттракторов.
Закон Боде касается пространственной характеристики солнечной системы. Но только ли квантифицированы радиусы планет или существуют определенные целочисленные соотношения между временными ритмами, которыми «дышит» система? Разумеется, действует третий закон Кеплера, устанавливающий определенные отношения между радиусами орбит rn и периодами обращения Tn ; напомним его:
.
Согласно этому закону периоды обращения планет уже не будут находиться в красивых дробно-рациональных отношениях. Однако, как мы сейчас увидим, в солнечной системе наблюдаются почти идеальные гармонические отношения между периодами обращения планет вокруг Солнца и периодами вращения планет вокруг собственной оси, о чём могли только мечтать Пифагор и Кеплер.
Мало кто обращает внимание на то, что 27,3-суточный период обращения Луны вокруг Земли, который мы обозначим T(Луна), странным образом совпал со средним осевым вращением Солнца, который мы обозначим τ(Солнце), и... средним менструальным периодом у женщин. Говорим «средним», поскольку скорость вращения Солнца вблизи полюсов заметно меньше, чем у экватора, котрый равен 32 суткам; менструальный период тоже, как известно, колеблется в достаточно широких пределах.
Спросят: причем здесь менструальный период? А притом, что все мы, живые существа, вышли из океана. По современным представлениям, жизнь на Земле, скорее всего, зародилась в прибрежных водах морей, где сильнее всего сказывалось влияние приливов и отливов, зависящее от пространственного расположения тройной системы Луна — Земля — Солнце. Когда имеется ряд почти равновероятных чисел: 26, 27, 28, 29, то на выбор периода колебаний начинают сказываться самые малоприметные причины. Вот и отреагировал женский организм на величину, которая на первый взгляд кажется абсолютно случайной; ее совпадение с периодом обращения Луны вокруг Земли и периодом вращения Солнца вокруг собственной оси не является таким уж случайным.
О том, какую важную роль в периодических процессах могут играть самые незначительные факторы, как раз и демонстрирует небесная механика, где было обнаружено огромное число орбитально-вращательных синхронизмов, наподобие того, который наблюдается в тройной системе Луна — Земля — Солнце и который можно записать как
=
= 1,
где Т — орбитальный период, а τ — осевой период. Этот тип синхронизма обусловливает тот простой факт, что Луна нам всегда видна одной и той же стороной. Механики до сих пор ломают голову над тем, какие решения могут иметь математические уравнения, описывающие систему трех тел, в то время как сама природа самым очевидным образом подсказывает им уже готовые стационарные решения, которые к тому же имеют строго дискретную форму.
Французский механик Лагранж (1735 — 1813), автор известной «Аналитической механики», в 1772 г. опубликовал небольшую работу, в которой проанализировал задачу трех тел. Им было получено одно частное решение, согласно которому два малых небесных тела могут перемещаться вокруг Солнца с одинаковой орбитальной скоростью, но которые разнесены по орбите на угол 60° (астрологи называют его секстилевым аспектом). Это аналитическое решение было подтверждено огромным числом астрономических наблюдений. В 1906 г. был впервые открыт астероид, получивший по одной астрономический классификации код 1906 TG, по другой — 588 Achilles, который шел впереди Юпитера на угловом расстоянии, равном как раз секстилю. Таким образом, был открыт первый троянец Ахиллес, названный в честь легендарного героя Троянской войны 1200 г. до Р.Х.
Собственно, Ахиллеса нужно было назвать греком, так как астрономы впоследствии разделили подобные астероиды, которых сейчас насчитывается около полутысячи, на две группы, а именно: те, что идут плотной группой впереди Юпитера называются греками, а те, что позади него — троянцами. Помимо Ахиллеса, к грекам относятся Гектор (1907), Нестор (1908), Агамемнон (1919), Одиссей (1930), а к троянцам — Патроклус (1906), Приамус (1917), Анеай (1930) (их места расположения на орбите Юпитера показаны на рис. 81). Часто между ними не делают никакого различия: всех, и греков и троянцев, именуют просто троянцами, как участников одного знаменательного события — «Троянской битвы» по решению великой задачи трех тел: астероид — Юпитер — Солнце. Одним из самых крупных троянцев является Гектор, имеющий вытянутую форму, но большая часть троянцев считается пока не открытой. По предварительной оценке, троянцев с радиусом, превышающим один километр должно быть не менее двух миллионов. В 1990 г. был обнаружен троянец у Марса, которого назвали Эврика.
Рис. 81
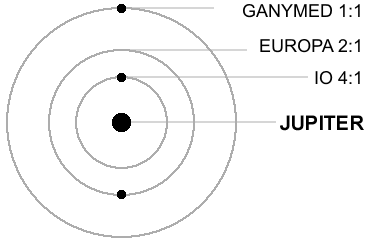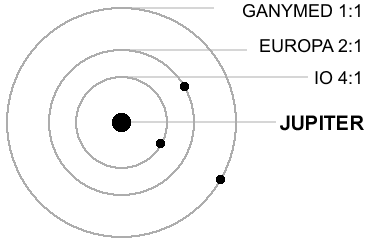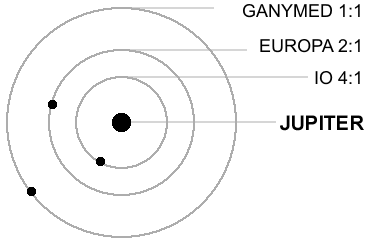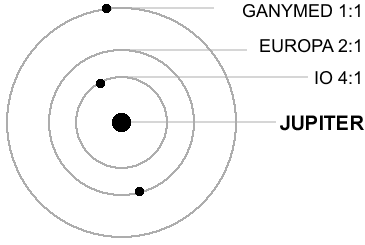
Существование троянцев, действие закона Боде и наличие в Солнечной системе различных синхронизмов — явления одного порядка, которые имеют одну и ту же дискретную природу. О сихронизмах или резонансных вращательных моментах писал еще Лаплас (1749 – 1827), во времена которого были хорошо известны отношения периодов обращения спутников Юпитера, открытых Галилеем в 1610 г. «... Период обращения первого спутника, — писал Лаплас, — равен приблизительно половине периода второго, который, в свою очередь, близок к половине периода третьего. Таким образом, средние угловые движения этих трех спутников следуют приблизительно половинной прогрессии. Если бы они точно следовали ей, то среднее движение первого спутника в сумме с удвоенным движением третьего было бы строго равно утроенному движению второго спутника. Но это равенство точнее, чем сама прогрессия, так что его можно рассматривать как точное, отнеся очень малые отклонения от него за счет ошибок наблюдений. Можно утверждать, что оно сохранится, по крайней мере, в течение длительного ряда веков.
Другой не менее странный результат, с такою же точностью полученный из наблюдений, заключается в том, что со времени открытия спутников средняя долгота первого без утроенной средней долготы второго плюс удвоенная такая же долгота третьего никогда не отличалась от двух прямых углов больше, чем на почти неощутимую величину. Эти два результата относятся также к средним движениям и средним синодическим долготам» [63, с. 96—97].
Аналогичные отношения периодов с небольшими отклонениями в кратности позднее были обнаружены в спутниковой системе Сатурна. Периоды (T) и расстояния до своих планет (R) для важнейших спутников Юпитера и Сатурна выписаны в табл. 45, ниже представлены синхронизмы.
Таблица 45
Планета Спутник Период
T (сутки)Расстояние
R (км)Юпитер Ио 1.769 421 600 Европа 3.551 670 900 Ганимед 7.155 1 070 000 Каллисто 16.689 1 883 000 Сатурн Мимас 0.942 185 520 Энцелад 1.370 238 020 Тефия 1.888 294 660 Диона 2.737 377 400
= 2.007,
= 1.590,
= 2.015,
= 1.596,
= 2.004,
= 1.595,
= 1.998,
= 1.588.
Присмотревшись внимательней к периодам обращения планет Солнечной системы, можно заметить другие любопытные отношения, в частности:
=
=
,
=
,
=
.
Следовательно, помимо сихронизмов, действующих на уровне системы спутников планет, существуют определенные резонансы в периодах обращения самих планет.
Если система Ио — Европа — Юпитер движется в пространстве наподобие систем с астероидами-троянцами (со времен открытия спутников они не сдвинулись относительно друг друга ни на одну угловую минуту), то, например, система Меркурий — Венера — Солнце выглядит уже не совсем стационарной. Существуют расчеты, которые свидетельствуют, что Меркурий и Венера когда-то были двойной планетой типа Луна — Земля. Потом Меркурий отдалился от Венеры на большое расстояние и вышел на самостоятельную аномальную орбиту вокруг Солнца с сингулярным числом Боде, равным –∞ (табл. 44). Имеется большая вероятность того, что Меркурий, в конце концов, упадет на Солнце, поскольку средний радиус его орбиты уменьшается. Луна тоже сейчас с довольно заметной скоростью удаляется от Земли и, видимо, придет время, когда она покинет Землю, отлетев на такое расстояние от нее, что угол между Луной, Солнцем и Землей составит величину, равную 60 угловых градусов, т.е. она станет троянцем. Другие устойчивые местоположения в Солнечной системе для нее не предусмотрены.
Такой сценарий возможен, однако здесь надо иметь в виду, что синхронизмы действуют не только в системе трех тел, типа Ио — Европа — Юпитер, Луна — Земля — Солнце, но и в системе четырех (Меркурий — Венера — Земля — Солнце) и даже пяти тел (Меркурий — Венера — Земля — Юпитер — Солнце). В самом деле, период обращения Меркурия равен 0,241 года, а период его осевого вращения — 58,7 дням, что составляет 0,161 в единицах земного года; разделив первое число на второе, убеждаемся в наличии гармонического отношения 3/2 между этими двумя периодами.
Точно такое же отношение для периодов имеет Венера, которая, в свою очередь, синхронно связана с обращением Земли вокруг Солнца. Таким образом, в Солнечной системе обнаруживаются гравитационные резонансы между тремя, четырьмя, пятью и, можно быть уверенным, шестью, семью и т.д. телами.
=
=
=
– 5 =
,
=
=
–
=
.
Если принять среднюю орбитальную скорость движения Земли за 1, то орбитальная скорость Меркурия будет равна V = 1,607270, а обратная ей величина равна Vi = 1/1,607270 = 0,622173. Ниже в табл. 46 приведены V и Vi для трех планет земной группы и трех газовых гигантов.
Таблица 46
| Планета | V | V i |
| Меркурий | 1,607270 | 0,622173 |
| Венера | 1,175794 | 0,850489 |
| Вен/Зем (s) | 0,855227 | 1,169280 |
| Марс | 0,810131 | 1,234369 |
| Юпитер | 0,438388 | 2,281082 |
| Юп/Сат (s) | 0,369135 | 2,709038 |
| Сатурн | 0,323812 | 3,088215 |
| Сат/Уран (s) | 0,280452 | 3,565672 |
| Уран | 0,228270 | 4,380783 |
Джон Харрис (John N. Harris) обнаружил следующие закономерности:
V Марс = Vi Сатурн – Vi Юпитер ,
V Уран = Vi Венера – Vi Меркурий .Если взять синодические (s) периоды планет, то выполняется еще одна разность, составленная из следующих отношений скоростей:
V Вен/Зем = Vi Сат/Уран – Vi Юп/Сат .
Сотни резонансных систем обнаружены в поясе астероидов. Самый первый был обнаружен, конечно, для Цереры. Как только Гаусс точно вычислил параметры ее орбиты, сразу же стало ясно, что апогей орбиты Цереры всегда находится вблизи перигелия Марса, а перигелий Цереры отстает от апогея Юпитера на 60°. Какие-то простые, т.е. троичные и четверичные, резонансы в поясе астероидов обнаружить легко; они возникают особенно часто между астероидами и одной из ближайших планет (реже, конечно, с Марсом, чем с Юпитером). Резонансные системы, включающие пять и более объектов, обнаружить, естественно, сложнее. Однако в поясе астероидов отчетливо прослеживаются так называемые люки Кирквуда. Что это такое, мы сейчас разъясним.
Американский астроном Дениел Кирквуд (1814—1895) еще в 1866 г., когда было известно менее сотни астероидов, заметил, что существуют дискретные провалы в распределении средних расстояний астероидов от Солнца, т.е. своеобразный обратный закон Боде, когда космическим телам не разрешено, а запрещено находиться в той или иной области пространства. Эти расстояния соответствовали периодам обращения вокруг Солнца, кратным периоду обращения Юпитера. В частности, дискретный принцип запрета распространялся на отношения 1 : 2, 1 : 3, 2 : 5 и 3 : 7, где первое число — период обращения астероида вокруг Солнца, второе — период обращения Юпитера вокруг Солнца (рис. 82).
Рис. 82
Последующее открытие многих сотен и тысяч астероидов только подтверждало существование люков Кирквуда: ни один из крупных астероидов не мог попасть в указанные щели. Таким образом, астрономы пошли не по пути разрешенных, а запрещенных устойчивых состояний. Кирквуд обратил также внимание на линейчатое строение кольца Сатурна.
На рис. 83 и 84 показаны фрагменты колец Сатурна, где видно, что светлые полосы чередуются с темными. Оказалось, что в одних случаях действуют запретительные квантовые законы, в других, — разрешительные (это видно и на рис. 82). Максимумы и минимумы освещенности определяются периодами обращения узких колец, которые находятся в кратных отношениях с периодами обращения спутников Сатурна. Американский космический аппарат «Вояджер 2» обнаружил около 100 000 узких колец. Так, в казалось бы сплошном кольце А, обнаружились группы колец, которые выглядят как стоячие волны (рис. 85 и рис. 86). Обнаружены практически пустые кольца, в которых, однако движутся крупные фрагменты тел (рис. 87). Совершенно неожиданным явлением оказалось наличие «спиц», т.е. поперечных темных волокон, охватывающих немалые площади кольца Сатурна (рис. 88). Таким образом, гравитационное взаимодействие между отдельными кольцами и спутниками сейчас выглядит намного сложнее, чем это представлялось Кирквуду.

Рис. 83

Рис. 84

Рис. 85

Рис. 86

Рис. 87

Рис. 88
Или вот еще один пример тайны классической механики. Известно, что Земля, двигаясь по своей орбите, вдруг неожиданно попадает в метеоритный поток. Отсюда Кирквуд сделал вывод, что метеориты также перемещаются плотными группами, траектории которых разрешены какими-то дискретными законами, которым, в свою очередь, подчиняются и кометы. Он, правда, предположил, что метеоритные группы являлись когда-то кометами, однако, в таком случае, непонятен механизм их распада. Теперь становится ясно, что метеоритные группы, по всей видимости, формируются из небольших разрозненных тел, находящихся далеко за пределами солнечной системы, но по мере приближения к Солнцу они успевают испытать на себе действие этого неизвестного дискретного закона и падают на Землю уже группами.
По этим же причинам нужно отвергнуть гипотезу, которая утверждает, будто пояс астероидов когда-то был цельной планетой под названием Фаэтон. Скорее всего, процесс шел обратный: из некогда сильно распыленного облака формировалось более или менее плотное кольцо. Кирквуд раскритиковал гипотезу Лапласа о монотонно-непрерывном образовании солнечной системы, возникшей якобы из гомогенного космического облака, как раз по причине того, что нынешнее состояние Солнечной системы слишком дискретно. По всей видимости, гравитационный закон, континуального характера, действует совместно с пока еще неизвестным нам дискретным законом тяготения, который имеет аттракторную природу.
О синхронизмах и законах миграции небесных тел сейчас стали немало писать, например [64], [65], [66]. Надо заметить, что математический аппарат дискретной гравитации находится пока в зачаточном состоянии, авторы указанных книг оперируют громоздкими формулами, многие из которых получены при аппроксимации эмпирического материала. Но и приведенных примеров вполне достаточно, чтобы уверенно сказать, что внутри солнечной системы действуют мощные квантовые механизмы отбора орбит, которые мы привыкли относить только для атомных и ядерных областей физики микроскопических размеров.
К сожалению, очень много интеллектуальных сил ушло на разработку пустых релятивистских теорий, так что ученым некогда было разрабатывать классическую физику. По существу, конструктивно думающие исследователи находятся пока что в самом начале пути познания мира гравитации. Сейчас они неуверенно переминаются с ноги на ногу примерно в том ее месте, которое отвечает открытию пифагорейцами гармонических дробей — октавы (1 : 2), квинты (2 : 3) и кварты (3 : 4). До серьезного использования дискретной математики, как это мы видели на примере численного решения уравнения Шредингера, пока еще дело не дошло. Можно надеяться, что теория аттракторов, связанная с принципом притяжения орбит к определенным стационарным уровням, еще скажет здесь свое веское слово.



