Эфир (Часть 14) Парадокс штриха
(Критика теории относительности)

О.Е. Акимов

Принято считать, что единицы длины и времени в движущейся системе координат K' сокращаются в соответствии с известным релятивистским множителем — корень квадратный из 1 – β² , где β = v/c — это отношение скорости движения системы K' относительно покоящейся системы K (скорость v) к скорости света c. В этом случае эталоны движущейся системы K' — Δx' и Δt' — получаются путем умножения эталонов покоящейся системы K — Δx и Δt — на указанный радикал.

Парадокс штриха

Но в 6-й части мы рассказали о парадоксе штриха. Оказалось, что в разных учебниках релятивистский радикал не обязательно сокращает эталоны длины и времени в движущейся системе K'. Он может увеличивать масштабные эталоны в системе K', так как для получения эталонов Δx' и Δt' не умножают, а делят эталоны Δx и Δt на релятивистский радикал. Причем операция деления может производиться только для одного эталона, другой эталон умножается на радикал. Таким образом, возникает четыре комбинации соотношения между эталонами движущейся K' и покоящейся K систем координат. Эта неопределенность нахождения эталонов и получила название парадокс штриха.

Здесь рассказывается о парадоксе штриха при эффекте Доплера

Сейчас я продемонстрирую парадокс штриха на конкретном примере двух книг: одна из них — известный учебник Ландау и Лифшица "Теория поля", автор второй книги Макс Борн; книга называется "Эйнштейновская теория относительности". Написана она в 20-м году прошлого века, так что на ней выросло не одно поколение физиков-релятивистов. Сейчас при изложении материала я воспользуюсь 6-м разделом курса лекций "Естествознание", выложенного на сайте Sceptic-Ratio.

Начнем с учебника Ландау и Лифшица. В нем, как это принято в подавляющем большинстве случаев, через штрихованную систему K' обозначена движущаяся система отсчета, а покоящуюся обозначают через K (без штриха).

Ландау (справа) и Лифшиц (слева)

Читаю вместе с вами: «Пусть в системе K покоится линейка, параллельная оси x, – пишут Ландау и Лифшиц. – Длина ее, измеренная в этой системе, пусть будет Δx = x2 – x1 (x2 и x1 – координаты концов линейки в системе K). Найдем теперь длину этого стержня, измеренную в системе K'. Для этого надо найти координаты обоих концов стержня (x'2 и x'1) в этой системе в один и тот же момент времени t'. Находим (имеются преобразования Лоренца для длины):

Преобразования Лоренца и формула сокращения длины
по курсу физики Ландау и Лифшица

Собственной длиной стержня называется его длина в той системе отсчета, в которой он покоится. Обозначим ее через l0 = Δx, а длину того же стержня в какой-либо системе отсчета K' – через l. Тогда (4.5) Таким образом, самую большую длину стержень имеет в той системе отсчета, где он покоится. Длина его в системе, в которой он движется со скоростью v, уменьшается в отношении (см. ниже) . Этот результат теории относительности называется лоренцевым сокращением».

Что называется собственной длиной стержня

Теперь смотрим, что пишет Макс Борн по этому же вопросу. «Итак, – пишет Борн, – мы должны определить длину линейки в системе S'(x', ct'), движущейся относительно S(x, ct)... Пусть l₀ – длина линейки в системе отсчета S', в которой линейка покоится; l₀ называют статической или собственной длиной линейки. Два конца линейки имеют координаты, скажем, x'₁ и x'₂, так что x'₂ – x'₁ = l₀ .

Макс Борн

При наблюдении этой линейки из системы S мы по первой из формул (70а) имеем (преобразования Лоренца для координат): (см. ниже фото)

Текст из книги Борна.

Полагая ..., мы можем записать ... (74) Эта формула утверждает, что длина линейки в системе S оказывается уменьшенной в отношении ... к 1 в точном согласии с гипотезой сокращения, предложенной Фитцжеральдом и Лоренцем».

Выражение (74).

Таким образом, Ландау – Лифшиц вывели формулу для лоренцева сокращения из прямых преобразований, а Борн – из обратных. То есть, выражения (4.5) и (74) в приведенных текстах только внешне выглядят одинаково, фактически они противоположного свойства.

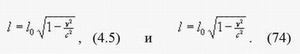
Выражения (4.5) и (74) только внешне выглядят одинаково,
фактически они противоположного свойства.

Люди гуманитарного склада ума, например, философы и журналисты, будут спорить до хрипоты, обсуждая запутанные тексты обеих книг. Но математику и программисту, имеющему дело с компьютером, разобраться в них ничего не стоит. Они еще раз выпишут два одинаковые формулы — (4.5) и (74), а рядом поставят равенства, которые имели в виду авторы, выражая х-координаты через l-отрезки длины. Ландау и Лифшиц приняли: l₀ = Δx и l = Δx' , а Борн ввел противоположные обозначения: l₀ = Δx' и l = Δx.

Противоположные обозначеия

Следовательно, Ландау и Лифшиц получили формулу (5.1), Борн — (5.2):

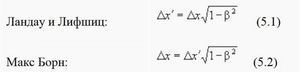
В данном случае абсолютно неважно, как авторы-релятивисты получали выражения (4.5) и (74); важно помнить об одном: штрихованная система — движется, нештрихованная — покоится. В итоге, авторы книг пришли к взаимоисключающему результату.

Сделаем короткий перерыв для разъяснения своей позиции в отношении длительности моих видеофильмов об эфире.

Видео-ролики из двух серий "Подделки" (древнеегипетских экспонатов, прежде всего, цветного бюста Нефертити) были преимущественно короткими, как это обычно рекомендуют для просмотра в YouTube, где-то около 15 минут. Теперь я не придерживаюсь этой рекомендации, так как не гоняюсь за количеством просмотров, а больше беспокоюсь о качественном составе аудитории, которая смотрит мои фильмы.

Видео-ролики из двух серий подделки бюста Нефертити были
короткими. Теперь я не придерживаюсь этой рекомендации.

Зачем мне посетители, которые постоянно дергают бегунок YouTube так, что из часового фильма просматривается 2-3 минуты. Так поступают лодыри, верхогляды, несерьезные люди. Я же заинтересован во вдумчивом зрителе, чтобы он смотрел мои работы от начала и до конца, а некоторые важные и сложные места — по несколько раз.

Так поступают лодыри, верхогляды, несерьезные люди.

В фильмах я часто делаю ссылки на страницы своего сайта Sceptic-Ratio, рассчитывая, что мой заинтересованный зритель продолжит изучение той или иной темы самостоятельно. В фильме не всегда можно всё показать и рассказать. Человеку непременно необходимо и что-то почитать, разобраться в математических доказательствах — иначе, зачем влезать в научную тематику.

Бойтесь легковесной популяризации, которой страдает почти вся продукция в Интернете. Как правило, в поисковиках она всплывает на первых позициях. В Сети можно найти всё, ознакомиться с любой точкой зрения; пытайтесь докопаться до сердцевины проблемы; не забывайте, что обычно дьявол сидит в деталях.

Я же заинтересован во вдумчивом зрителе.

Поэтому, дорогой наш зритель и слушатель, наберитесь терпения и продолжите вместе со мной чтение учебника Ландау и Лифшица и книги Макса Борна, где рассказывается об изменении эталонов длины и времени. Поверьте мне, тема парадокса штриха — одна из важнейших. Люди проживают многие гола, пытаясь разобраться в релятивистских спекуляциях. Так посвятите же сегодняшний день данной запутанной проблеме, чтобы в будущем не плутать в темных лабиринтах теории относительности.

Итак, выясним, как уважаемые авторы учебника "Теория поля" и книги "Эйнштейновская теория относительности" представили своим несчастным читателям тему "Замедления времени" — центральную для релятивистской ортодоксии.

Начнем с учебника Ландау и Лифшица.

«Предположим, – пишут они, – что мы наблюдаем из некоторой инерциальной системы отсчета произвольным образом движущиеся относительно нас часы. В каждый отдельный момент времени это движение можно рассматривать как равномерное. Поэтому в каждый момент времени можно ввести неподвижно связанную с движущимися часами систему координат, которая (вместе с часами) будет являться тоже инерциальной системой отсчета».

Предположим, что мы наблюдаем из некоторой инерциальной системы отсчета.

Далее авторы зачем-то использовали дифференциальную форму записи, хотя с точки зрения физики ситуация осталась прежней: изменение временной координаты (t) будет таким же, что и изменение пространственной координаты (x). Окончательную формулу (3.2) можно записать формулой (5.3)

Вывод производится через квадрат интервала путем принятия условия Δx' = 0

Самым удивительным в учебнике Ландау и Лифшица является последний абзац приведенного пассажа: "Как видно из формулы (3.1) и (3.2), — пишут авторы, — собственное время движущегося объекта всегда меньше, чем соответствующий промежуток времени в неподвижной системе. Другими словами, движущиеся часы идут медленнее неподвижных».

Теперь посмотрим, что написал Борн в своей книге относительно изменения временной координаты. В первом предложении цитируемого отрывка он противоречит выводам учебника Ландау и Лифшица:

Для того чтобы вычислить величину удлинения ...

Итак, Ландау и Лифшиц имели в виду укорочение (сокращение) долготы; Борн сразу заявил об удлинении (увеличении) времени. Далее, используя по-прежнему обратные преобразования Лоренца, он вывел формулу (75), которая в наших обозначениях выглядит как формула (5.4)

Это удлинение (замедление) времени
противоположно по характеру сокращению длины.

В конце отрывка Борн еще раз недвусмысленно заявил: «Это удлинение (замедление) времени противоположно по характеру сокращению длины. Разумеется, с обратной точки зрения единица времени по часам, покоящимся в системе S, оказывается увеличенной в системе S'... Время, которое показывают часы, покоящиеся в выбранной системе отсчета, называется собственным временем системы».

Изменение координат в движущейся системе К' относительно покоящейся системы К у Борна совпали с формулами, представленными в работах Эйнштейна и Паули, хотя вывод их отличается от вывода Борна. Комбинация формул в Берклеевском курсе и в курсе Левича отличаются не только логикой вывода, но и результирующими комбинациями математических выражений. Откуда же взялся такой разнобой в формулах, который мы видим по таблице 5.1?

Дело в том, что при выводе окончательных формул релятивисты смешивают себя, как субъекта теории (его называем метанаблюдателем), с объектными наблюдателями, находящимися в координатных системах К и К'.

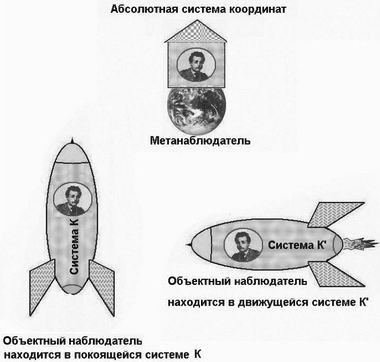
Авторы, цитируемых нами книг, становятся метанаблюдателями.

Авторы, цитируемых нами книг, становятся метанаблюдателями неосознанно. Их внимание периодически соскальзывает то на позицию субъекта теории, то объекта, причем один раз их угораздит оказаться в штрихованной системе отсчета, другой раз — в нештрихованной. Так, появляется неопределенность в расстановке штриха, поскольку они, как метанаблюдатели, постоянно витают где-то над обеими системами, смешивая, что относительно чего движется. Им порою, кажется, что сначала штрихованный эталон больше нештрихованного, затем — наоборот.

Метанаблюдатели

Метанаблюдатель выказывает свое присутствие, в частности, через термин собственный: если объектный наблюдатель к своим эталонам длины и времени добавляет этот предикат, значит, он претендует на статус метанаблящателя. Собственные эталоны длины и времени определяются как длина отрезка и, соответственно, время таких часов, которые покоятся относительно системы отсчета.

Выбор в принципе не возможен.

Однако, если придерживаться этой дефиниции, легко выявится ее достаточно бессмысленное содержание. Часы, принадлежащие непосредственно данной системе координат, с точки зрения той же теории относительности, показывают то, что они показывают, как бы это тавтологично не звучало, т.е. Δt = Δt, Δt' = Δt' — не нужны эти вторичные обозначения. Когда под предлогом собственного времени и длины вводят новые обозначения, например, l₀ = Δx и l = Δx' или Δt = T₀ и Δt' = T и т.д. – если это вы видите, знайте, вас хотят ввести в заблуждение.

Ясно, что существовать могут только два эталона часов или два течения времени – время. Третьего времени, как бы его не называли – собственное или еще как-то – просто быть не может. Оно исключено логикой построения возможных ситуаций.

Мысленно релятивисты скользят как бы по ленте Мёбиуса.

Мысленно релятивисты скользят как бы по ленте Мёбиуса. Рассуждая сначала в одной плоскости, они незаметно для себя оказываются в другой плоскости, развернутой относительно первой на 180 градусов. Такой логический кульбит объектный наблюдатель способен совершать благодаря абсолютной системе координат метанаблюдателя. Раздвоение сознания — это естественное и постоянное состояние любого релятивиста.

Раздвоение сознания — это естественное и
постоянное состояние любого релятивиста.

Парадокс штриха, связанный с масштабами длины и времени, напоминает парадокс лестницы Шрёдера. Глядя на рис. 6.1, может возникнуть образ либо лестницы, либо нависающего ступенчатого карниза. Почему так происходит?

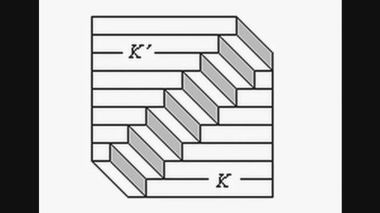
Лестница Шрёдера.

Другое дело, если смотреть не на симметричный рисунок 6.1, а на реальную лестницу или карниз. За счет перспективы, которая выражается, скажем, в чуть меньшем расстоянии между горизонтальными полосками треугольника K'. Тотальный релятивизм не оставляет нам ни единого антисимметричного элемента в отношении систем K' и K.

Реальная лестница за счет перспективы имеет антисимметричный элемент.

Поэтому сначала к нам приходит уверенность в правильности использования обратных преобразований Лоренца, но через некоторое время эта уверенность куда-то улетучивается, картина переворачивается, и мы уже считаем правильным использование прямых преобразований. Это происходит периодически, мы не можем остановиться на каком-то одном решении, которое следовало бы назвать истинным.

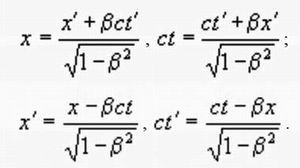
Прямые и обратные преобразования Лоренца

Психологический парадокс штриха определенным образом связан и с известным логическим «парадоксом обманщика», который строится следующим образом: «Я обманщик», – сказал обманщик. (см. Парадоксальные высказывания и Построение доказательств в логике высказываний). Итак, обманщик сообщает о себе, что он является таковым. Следовательно, он выступает в своем противоположном качестве, а именно, необманщика. Поэтому сказанное предложение нужно прочитать так: «Я обманщик», – сказал необманщик. Правдивому человеку мы должны верить, но ведь он сообщает, что он является обманщиком. Таким образом, мы снова возвращаемся к первому предложению.

«Я обманщик», – сказал обманщик.

Возникает неопределенность в том, как квалифицировать фразу, заключенную в кавычках: как нечто, соответствующее истине, то есть считать, что она верно характеризует человека, произносящего данное предложение, или же ее надо расценить как ложную фразу.

Парадокс обманщика возник потому, что в данной семантико-лингвистической конструкции не проведена демаркационная линия между субъектом и объектом. Помимо обманщика и необманщика в этой ситуации участвуем мы с вами в роли исследователя, стороннего наблюдателя или, как мы говорим, метанаблюдателя.

Возникает неопределенность в том, как квалифицировать
фразу «Я обманщик» – как истинную или как ложную.

Если произвести четкое лингвистическое отделение смыслового содержания, которое должно относиться к нам, как метанаблюдателям, от прочей семантики объектных персонажей, то логическое противоречие будет снято. Вот каким способом нужно представить ситуацию с обманщиком, чтобы исключить из нее двусмысленность:

Как произвести лингвистическое отделение смыслового
содержания, высказанное наблюдателем и метанаблюдателем?

1. «Я обманщик», – сказал обманщик.
«Это истина», – сказал метанаблюдатель.

2. «Я обманщик», – сказал необманщик.
«Это ложь», – сказал метанаблюдатель.

3. «Я необманщик», – сказал обманщик.
«Это ложь», – сказал метанаблюдатель.

4. «Я необманщик», – сказал необманщик.
«Это истина», – сказал метанаблюдатель.

Помимо обманщика и необманщика в этой ситуации
участвуем мы с вами в роли метанаблюдателя

Парадокс обманщика предупреждает нас о возможных на этом пути осложнениях. Из цепочки отношений – Петр враг Ивана, Иван друг Степана, а Степан враг Кузьмы – однозначно следует, что Петр друг Кузьмы. Этот вывод сделан субъектом теории, т.е. метанаблюдателем.

«Я — Ян», «Я — лгунишка».

Но нельзя строить конструкцию типа: «Петр обманщик», – сказал Иван. «Это ложь», – сказал Степан. Степан, как объектный персонаж, не должен выносить свою оценку в отношении Петра, Ивана и прочих лиц, непосредственно участвующих в объектной ситуации. Это разрешено делать только метанаблюдателю с безупречной «моральной» характеристикой, который не имеет права лгать.

За любым «наблюдателем» всегда
следит какой-нибудь метанаблюдатель.

Таким образом, парадокс обманщика говорит нам о том, что попытка метанаблюдателя встать на позицию обманщика или необманщика немедленно приводит к смысловому конфликту.

Добавление из первоначального курса лекций "Естествознание"



Два пассажира сидят каждый в своем купе и смотрят в окна

Представим себе два железнодорожных состава, неподвижно стоящих на соседних путях. Два пассажира, находясь в своих поездах, смотрят в окна вагонов друг на друга. Увиденную ими картину можно отразить следующей таблицей умножения:

1) движение * движение = покой,
2) покой * движение = движение,
3) движение * покой = движение,
4) покой * покой = покой.

При плавном движении двух поездов в одном направлении и с одинаковой скоростью пассажирам кажется, что их поезда стоят на месте (1), как если бы оба поезда действительно стояли на месте (4), т. е. возникает неопределенность в выборе пунктов 1 и 4. При плавном движении одного из поездов пассажиры также не в состоянии определить, какой именно из поездов тронулся (неопределенность между пунктами 2 и 3). Объективную ситуацию с движением поездов может правильно оценить лишь провожающий, находящийся на платформе, т. е. метанаблюдатель.

Точно такая же неопределенность возникает в теории относительности при сравнении эталонов длины и времени, находящихся в движущейся и покоящейся системах отсчета. Нельзя построить физическую теорию, основывающуюся исключительно на относительных величинах. Логика и математика подсказывают нам необходимость введения метанаблюдателя, находящегося в абсолютной системе отсчета. Тогда преобразования Лоренца можно будет привязать к этой абсолютной системе отсчета, которой для Лоренца служил эфир.

Если абсолютная система отсчета отсутствует, каждый из объектных наблюдателей произвольно выбирает либо прямые, либо обратные преобразования координат и получает на их основе то, что ему нравится. Без абсолютной системы отсчета объектный наблюдатель оказывается как бы без точки опоры, т.е. в роли барона Мюнхгаузена, который вытащил самого себя из болота за волосы.

В своих мысленных экспериментах релятивисты не вводят метанаблюдателя, но всякий теоретизирующий человек не может абстрагироваться от самого себя, поэтому метанаблюдатель находится на положении «нелегала». Он проявляется то в образе одного объектного наблюдателя, то другого; совершенно незаметно для себя он будет то «расщепляться» на два наблюдателя, находящихся каждый в своей системе, то вновь «конденсироваться» в одно лицо.

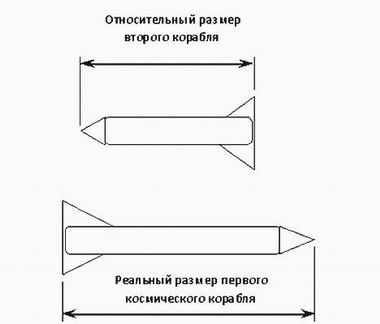
Метанаблюдатель, находясь в некотором привилегированном положении, всегда претендует на абсолютную непогрешимость в своих суждениях. Когнитивные процессы, идущие в недрах сознания субъекта теории, генерируют собственный пространственно-временной объем. Хочет он того или нет, метанаблюдатель всегда занимает абсолютную систему отсчета; такая позиция неизбежна, иначе невозможно было бы сравнение, а значит, и мышление.

Сокращение длины движущихся объектов.
С этим, кажется, все согласны и релятивисты
не ожидают здесь какого-то логического подвоха.

Смешение функций объектного наблюдателя с субъектным открывает шлюзы для всевозможного рода спекуляций, которые мы и наблюдаем на примере неопределенного изменения эталонов длины и времени. В общем, в зависимости от ситуации в системах отсчета могут устанавливаться такие отношения, которые удобны с точки зрения общей идеологии теории относительности, но ошибочные по существу.

"Почему он?! На этот вопрос учителя
ответить учащемуся очень сложно.

См. фильм с этим текстом

http://youtu.be/Qhz9wRqT6aU