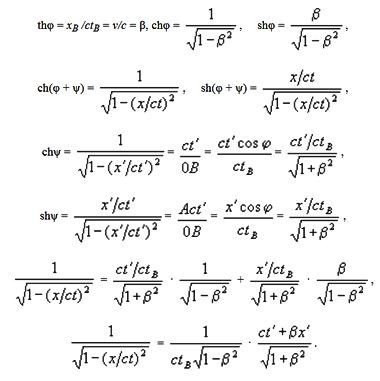Эфир (Часть 15)
Почему нет пространства Минковского
(Критика теории относительности)

О.Е. Акимов

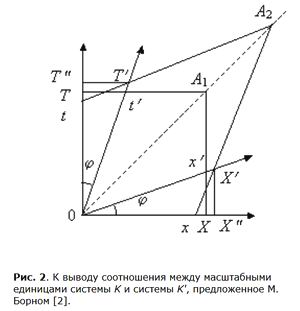
Если вы школьный учитель или вузовский преподаватель, у которого в программе стоит тема "Теория относительности", попробуйте построить одно практическое задание следующим образом. Попросите учащихся или студентов вычертить диаграмму Минковского и определить по ней реальный масштабный коэффициент сокращения длины и времени. Здесь имеется проблема, которой мы касались в 6-й части видеофильма "Эфир". Напомним, в чём она заключается.

Здесь рассказывается о парадоксе штриха при эффекте Доплера

Принято считать, что единицы длины и времени в движущейся системе координат K' сокращаются в соответствии с известным релятивистским множителем — корень квадратный из 1 – β² , где β = v/c — это отношение скорости движения системы K' относительно покоящейся системы K (скорость v) к скорости света c. В этом случае эталоны движущейся системы K' — Δx' и Δt' — получаются путем умножения эталонов покоящейся системы K — Δx и Δt — на указанный радикал.

Парадокс штриха

Но в 6-й части мы рассказали о парадоксе штриха. Оказалось, что в разных учебниках релятивистский радикал не обязательно сокращает эталоны длины и времени в движущейся системе K'. Он может увеличивать масштабные эталоны в системе K', так как для получения эталонов Δx' и Δt' не умножают, а делят эталоны Δx и Δt на релятивистский радикал. Причем операция деления может производиться только для одного эталона, другой эталон умножается на радикал. Таким образом, возникает четыре комбинации соотношения между эталонами движущейся K' и покоящейся K систем координат. Эта неопределенность нахождения эталонов и получила название парадокс штриха.

В самом начале этого видеофильма мы упомянули диаграмму Минковского, сказав, что было бы желательно вычертить конкретную диаграмму и определить по ней реальный масштабный коэффициент сокращения длины и времени. Релятивисты, как правило, даже не пытаются этого сделать. Анализ проводится на уровне формул. Но сейчас мы столкнулись с неоднозначностью в оценки эталонов длины и времени. Поэтому было бы логично прибегнуть к геометрическим чертежам, которые помогли бы нам установить истину, а именно, узнать, будет ли

Δx < Δx'     или     Δx > Δx',       Δt < Δt'     или     Δt > Δt' .


Герман Минковский

21 сентября 1908 года на 80-м собрании немецких естествоиспытателей и врачей в Кёльне Герман Минковский сделал доклад под названием "Пространство и время". В ходе доклада докладчик вычертил рис. 1 и попытался доказать, что эталоны движущейся и покоящейся системы K(x, t) и K'(x', t') связаны посредством релятивистского радикала.

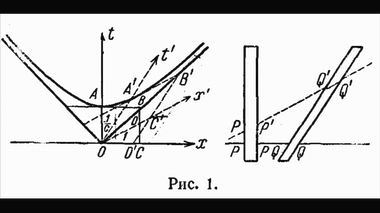
Рис. 1 из работы Минковского. Автора расхваливают на все лады за эту диаграмму и введение им четырехмерного пространства. На самом же деле Минковский наделал здесь грубые математические ошибки, которые раскроются перед нами по ходу продвижения нашего анализа, хотя кое о чём можно сказать сразу. Из левого чертежа (рис. 1) автор вывел ложную формулу для сокращения длины, т.е. отношение длины отрезков OC к OD' или PP к QQ. Но почему-то он даже не попытался вывести аналогичное отношение для времени. Почему? Да потому, что в 1909 году господствовала точка зрения Эйнштейн, согласно которой отношение эталонов длины противоположно отношению эталонов времени, т.е. Δx/Δx' = Δt'/Δt. Диаграмма же, вычерченная автором, оказалась абсолютно симметричной относительно биссектрисы ОВ(В'). Следовательно, Минковский должен был получить Δx/Δx' = Δt/Δt'. Однако открыто объявить о расхождении своего геометрического вывода с аналитическим выводом формулы замедления времени, сделанным Эйнштейном (тоже, конечно, ложным), он не решился.

Автор доклада упомянул об отрицательном результате эксперимента Майкельсона и напомнил, что "по Лоренцу, каждое движущееся тело должно сократиться в направлении движения при скорости v в отношении ... (см. текст 1 ниже на фото)

Текст 1 из статьи Минковского

Я хочу теперь на нашем чертеже, — сказал Минковский, — показать, что гипотеза Лоренца и новые воззрения на пространство и время вполне эквивалентны и что благодаря этому гипотеза делается гораздо понятнее. Если с целью упрощения отвлечься от координат y и z , представить себе пространственно одномерный мир, то параллельная полоса, стоящая прямо, как ось t, и параллельная полоса, наклоненная относительно оси t (рис. 1), суть графики покоящегося и равномерно движущегося тела, сохраняющего в обоих случаях одно и то же постоянное пространственное протяжение".

После некоторых разъяснений в построении чертежа (рис. 1) докладчик заявил: "Из простого расчета следует, что если dx/dt = v, то ... (см. текст 2 ниже на фото)

Текст 2 из статьи Минковского.

Итак, Минковский утверждает, что в движущейся системе K' отрезок OD' на левом чертеже или отрезок QQ на правом чертеже меньше эталона длины в покоящейся системе K, где за эталон принят отрезок OC и отрезок PP. В наших обозначениях справедливо выражение (5.1).

Поскольку диаграмма Минковская симметрична относительно биссектрисы ОB или OB', соответствующей скорости света (c = x/t = x'/t'), то соотношения эталонов времени будет таким же, как и отношение отрезков длины, т.е. справедливо выражение (5.3).

Таким образом, правильной оказывается комбинация эталонов, представленная в учебнике Ландау и Лифшица; три других комбинации из таблицы 5.1, включая самую первую, предложенную Эйнштейном, а потом Борном и Паули, будут уже ложными.

Парадокс штриха

Итак, три первых автора пали жертвой парадокса обманщика. Минковский же с помощью элементарной геометрии нашел, кажется, единственно правильное решение. Первым ошибся Эйнштейн, когда искал соотношения между масштабными единицами движущейся и покоящейся системы координат. Борн и Паули шли сразу за ним уже по ложному пути. Ландау и Лифшица, видимо, учли геометрический урок, преподанный Минковским. Но почему другие релятивисты не последовали за Минковским — это загадка, которая, однако, имеет некоторое объяснение.

Дело в том, Минковский тоже ошибся в количественном отношении: формулы (5.1) и (5.3) ошибочны, так как ошибочны выражения в самом докладе Минковского.

А. Зоммерфельд

То, как выводил эти формулы Минковский, повторил Зоммерфельд. Но если бы эти авторы подставили какие-нибудь числовые значения в эти выражения, они тут же убедились бы, что формулы не работают. Соотношение между отрезками OC и OD' или между PP и QQ совсем не такое, как хотели бы видеть указанные авторы и все прочие релятивисты.

Текст ошибочного доказательства
сокрашения длины по диаграмме Минковского

Для понимания того, в чём ошибся Минковский, воспользуюсь курсом Дискретной математики подразделом Ортогональные и гиперболические преобразования раздела 2.5. "Пространственные группы и двойственность".

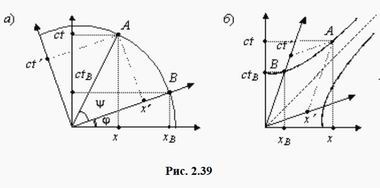
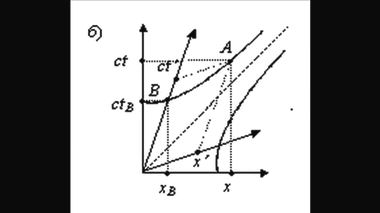
Под ортогональными и гиперболическими преобразованиями понимаются повороты осей, показанные на рис. 2.39 (а) и (б), соответственно. Обозначения осей координатных систем K(x, ct) и K'(x', ct') здесь выбраны с прицелом на теорию относительности, хотя рассматриваемый вопрос относится к общематематической тематике.

Ортогональный поворот осей ищется по тригонометрическим формулам сложения двух углов, если радиус окружности равен единице:

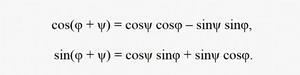
Непосредственно из чертежа видно, что

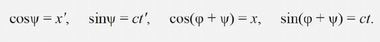
Следовательно,

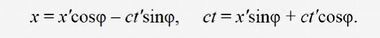
Так как

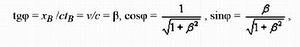
окончательно получаем первые две формулы ортогонального преобразования в форме декартового поворота, который соответствует первым двум формулам первого столбца табл. 2.92 (в таблице ось ct обозначена через y)

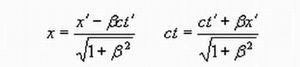
Если найденные преобразования принять за прямые, то обратными будут две другие формулы, первого столбца табл. 2.92.

Рассмотренные преобразования действуют в евклидовом пространстве. Чтобы получить из них гиперболические преобразования для псевдоевклидового пространства, нужно произвести замену вещественной оси y на мнимую ось iy (i — базисная единица). В этом случае произойдет замена вещественного параметра β на –iβ, так как x/iy = –iβ. Формулы гиперболического поворота, полученные из формул ортогонального преобразования, заняли второй столбец табл. 2.92.

Согласно принципу двойственности, который действует в некоторых областях геометрии, логики, физики и других наук (о нём рассказывалось в предыдущем подразделе Двойственность и проецирование), мы можем получить гиперболические преобразования в евклидовом пространстве (это третий столбец табл. 2.92). Тогда ортогональные преобразования окажутся в неевклидовом пространстве с мнимой вертикальной осью iy (это четвертый столбец).

Нас интересует изменение масштаба осей при гиперболическом повороте. Как чаще всего поступают релятивисты? Они обнуляют одну из координат. Например, чтобы найти изменившуюся длину Δx' штрихованной системы K' по известной длине Δx нештрихованной системы K, берут координаты двух точек на оси абсцисс и составляют из них разность. Как правило, релятивисты пользуются формулами без мнимой единицы, т.е. формулами третьего столбца таблицы 2. 92.

Итак, беря две точки на оси x-ов, и составляем из них разность:

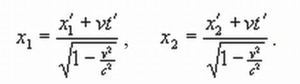
При условии одновременного измерения пространственных координат, т.е. выполнения условия t₁ = t₂, получается формула сокращения длины:

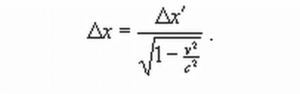
Очевидно, аналогичная методика нахождения соотношения между масштабами штрихованной и нештрихованной системы координат должна срабатывать и для ортогональных преобразований декартовых координат. Выписываем координаты

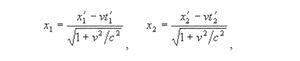
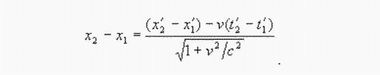
Обращаем внимание, что в знаменателе стоит не релятивистский радикал. При условии t₁ = t₂ получаем формулу удлинения длины:

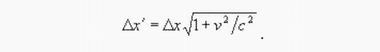
Но при повороте декартовых координат масштабы осей, как известно, не меняются. В действительности полученное соотношение

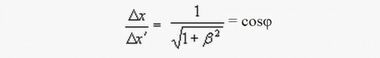
этот косинус указывает на угол поворота оси. Следовательно, методика релятивистов ошибочна.

Каким же образом нужно поступать, чтобы рассчитать соотношение между масштабами штрихованной и нештрихованной систем координат при гиперболическом повороте, который показан на рис. 2.39б?

Для нахождения масштабного или нормировочного коэффициента kn слегка дополним рис. 2.39а, как это показано на рис. 2.40.

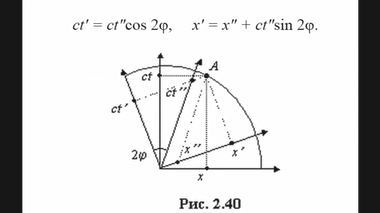
Из последнего чертежа найдем координаты:

ct' = ct"cos 2φ,         x' = x" + ct"sin 2φ.

Подставим найденные штрихованные значения в формулу преобразования декартовой пространственной координаты:

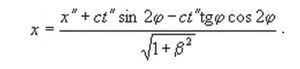
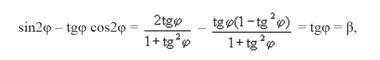
окончательно находим масштабный коэффициент k_n:

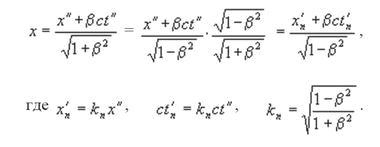
Аналогичным образом можно выделить масштабный коэффициент k_n из второго ортогонального преобразования:

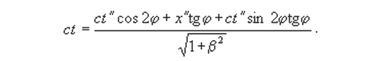
Так как cos2φ + tgφ sin 2φ = 1, окончательно находим:

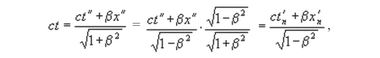
Для проверки найденного масштабного коэффициента k_n можно вычертить реальный чертеж на бумаге с гиперболическим поворотом осей x' и ct', отвечающий преобразованиям Лоренца, и произвести измерение всех координат непосредственно по чертежу.

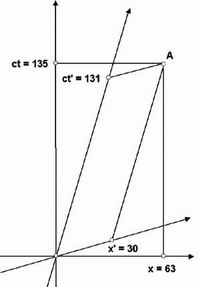
Реальный чертеж на бумаге с гиперболическим поворотом осей x' и ct'

Кроме точки A, возьмем еще четыре точки — B₁, B₂, C₁, C₂, — с другими координатами. Все измеренные величины занесены в табл. 2.93.

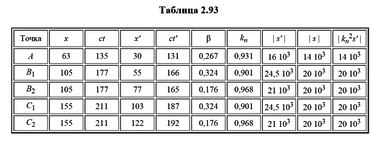
По найденным координатам вычислим β и масштабный коэффициент k_n, а также квадратичные инварианты s и s' по формуле, известной из теории относительности:

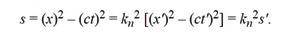
Надо заметить, что коэффициент k_n определяется из квадратичной формы намного проще. Добавим, поскольку коэффициента k_n < 1, то можно говорить о «сжатии» обеих штрихованных осей. Однако из этого математического факта вовсе не следует, что в реальном физическом мире сокращается пространство и замедляется время. Любые математические манипуляции с веденными нами координатами никак не сказываются на физических явлениях. Релятивист тем и отличается от антирелятивиста догматической верой, будто выбор геометрического пространства и его математические преобразования отражаются на физических процессах.

Нельзя не заметить также, что в получении преобразований, соответствующих диаграмме Минковского, был использован искусственный прием: умножение числителя и знаменателя формул преобразований на релятивистский радикал.

Это понадобилось нам для того, чтобы гиперболическими преобразования (*), геометрически соответствующие диаграмме Минковского, чисто внешне отвечали преобразованиям Лоренца. Для самих же преобразований (*) — их нельзя уже называть лоренцевыми — не нужно вводить никаких масштабных коэффициентов. Для проверки данного математического факта найдите конкретные числовые значения координат x и ct (см. табл. 2.93) путем прямой подстановки в преобразования (*) числовых значений координат x' и ct'.

Таким образом, диаграмма Минковского, вообще говоря, не удовлетворяет преобразованиям Лоренца. Но их внешнего сходства можно добиться путем введения найденного выше масштабного или нормировочного коэффициента k_n .

Релятивисты часто пользуются трехмерной диаграммой Минковского, на которой имеется две пространственные оси (x, y), образующие горизонтальную плоскость, и одна вертикальная ось t. Третью пространственную ось z они не вычерчивают, но ее существование подразумевается. На диаграмме указывается положение объектного наблюдателя в центре координат.

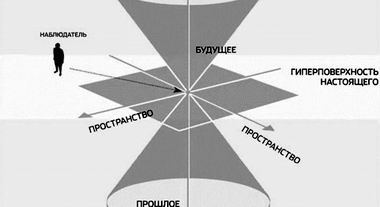
Трехмерная диаграмма Минковского

Это его положение соответствует настоящему времени; вверх от него откладывается будущее время (+ t), вниз от него — прошлое время (– t). Поверхность конуса, заверяют релятивисты, ограничивает возможные траектории наблюдателя в четырехмерном пространстве-времени. Они рассказывают о мировых линиях (vt), пролегающих внутри конуса; на границе же конуса скорость v достигает скорости света.

Трехмерные диаграммы Минковского обычно рисуются схематично, без каких-либо количественных оценок. Между тем, все числовые величины, присвоенные этим трехмерным сооружениям, будут содержать все те же ошибки, которые отмечались для двумерных диаграмм Минковского.

Таким образом, диаграмма, которую релятивисты называют именем Германа Минковского, носит исключительно двумерную природу. Попытка экстраполировать ее на пространство трех и большего числа измерений — математически бессмысленна.

В силу принципа двойственности, который обнаруживается через замену вертикальной оси y = ct на мнимую ось iy = ict и что отражено в таблице 2.92 двумя рядами дублирующих формул, мы можем вместо косинуса и синуса использовать гиперболические функции.

Таким образом, комплексную плоскость с системой уравнений из тригонометрических функций

cos(φ + ψ) = cosψ cosφ – sinψ sinφ,
sin(φ + ψ) = cosψ sinφ + sinψ cosφ

можно заменить вещественной плоскостью с системой гиперболических функций:

ch(φ + ψ) = chψ chφ + shψ shφ,
sh(φ + ψ) = chψ shφ + shψ chφ;

Таким образом, из чертежа (рис. 2.39б) мы выведем преобразования Лоренца, в которых, однако, уже учтены изменения масштабных единиц штрихованной системы (см. Масштаб осей при гиперболическом повороте).

Остается рассмотреть маленький, но очень важный вопрос, связанный с грубой математической ошибкой предельного перехода. Напомним, как релятивисты осуществляют его. Они записывают преобразования Лоренца в виде

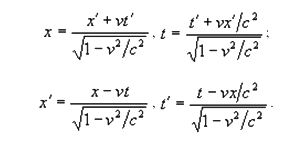
Затем говорили, что условие v << c равносильно условию c → ∞, следовательно, преобразования Лоренца переходят в преобразования Галилея

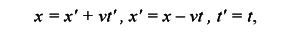
Ошибка данного предельного перехода легко обнаруживается при рассмотрении двух принципиально различных движений координатных систем K и K' относительно друг друга. Преобразования Лоренца — это вращательное движение осей — пусть гиперболического характера — преобразование Галилея — это поступательное или продольное смещение осей

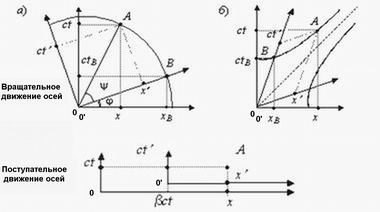
Не может вращательное движение осей в пределе переходить в их поступательное движение, когда начало координат системы K' (т.е. точка 0') удаляется на какое-то расстояние от начала координат системы K (точка 0).

Где допустили ошибку релятивисты?

Ошибка возникла тогда, когда условие предельного перехода β = v/c → 0 заменили неравносильным условием c → ∞

Поэтому преобразования Лоренца лучше писать не в виде, в котором скорости v и c фигурируют раздельно, а в виде преобразований, в которых v и c связаны одним параметром β = v/c

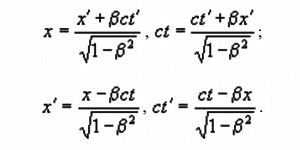
При условии β → 0 или φ → 0 гиперболические функции ведут себя следующим образом:

Отсюда следует, что преобразования Лоренца в случае предельного перехода параметра β → 0 трансформируются в единственно возможные равенства: x = x', ct = ct'. Никаких других выражений здесь в принципе быть не может.

Итак, казалось бы, крохотная подмена условий предельного перехода привела к колоссальным заблуждениям, будто преобразования Лоренца это те же самые преобразования Галилея, но только записанные для очень большой скорости v , сопоставимой со скоростью света c . Это, разумеется, не так.

Многим релятивистам известна обратная процедура, а именно вывод преобразований Лоренца из преобразований Галилея. Он не связан с каким-либо предельным переходом. Преобразования Лоренца получаются из преобразования Галилея путем единственного допущения: скорость света в штрихованной K' и нештрихованной системе K координат должна быть одна и та же:

x/t = x'/t' = c = const.

x = (x' + vt' )α,         x' = (x – vt)α,

Из этих равенств не сложно получить искомый множитель α

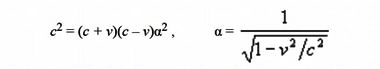
Таким образом, переход от Галилея к Лоренцу будет скачкообразным, он не является предельным переходом, т.е. непрерывным изменением параметра β. Условие постоянства параметра c в штрихованной и нештрихованной системах не накладывает на саму величину c никаких количественных ограничений, т.е. c может быть вполне сопоставима со скоростью v или даже меньше ее (c < v), преобразования Лоренца по-прежнему остаются в силе.

Трансформация поступательного преобразований Галилея во вращательное преобразование Лоренца означает трансформацию одной группы симметрии в совершенно другую группу симметрии. Группа преобразований Галилея не является подгруппой преобразований Лоренца или наоборот. Это — две различных группы симметрии.

Ошибка предельного перехода моментально приводит к множеству противоречий, которые не имеют никакой перспективы для разрешения. Парадокс распиленной линейки является наиболее наглядным — о нем сейчас мы расскажем.

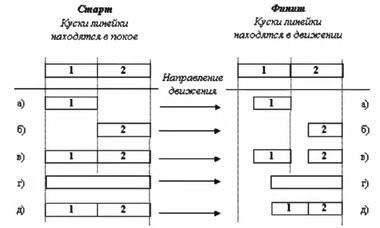
Рис. 8.2. Парадокс распиленной линейки.

Пусть происходит транспортировка двух кусков линейки — 1 и 2. Если куски транспортируются по отдельности, то сокращение их произойдет так, как показано на финише (а) и (б). Совместная транспортировка этих кусков ничего не изменит и на финише между кусками будет виден просвет (в). Однако транспортировка целой линейки приведет к сокращению типа (г). Значит, между кусками не должен наблюдаться просвет (д) — ведь линейка «не знает», что она распилена. Итак, непонятно, как будет в действительности происходить сокращение транспортируемых кусков линейки — по варианту (в) или по варианту (д)?

Дадим разъяснения к парадоксу распиленной линейки.

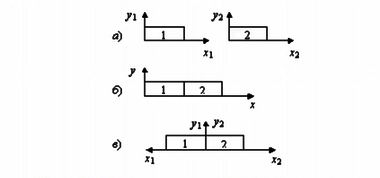
Рис. 8.3. Дрейф нуля системы отсчета.

Случай (а) соответствует варианту (в) на рис. 8.2, когда каждый кусок линейки связан со своей собственной системой отсчета. Случай (б) соответствует варианту (д) на рис. 8.2, когда оба куска линейки связаны одной системой координат. Случай (в) демонстрирует иное, чем для случая (а), расположение координатных осей. Какую систему координат выбрать для наших кусков линейки? В действительности, это дело вкуса каждого человека.

В парадоксе с распиленной линейкой проявляется эффект, который можно было бы назвать дрейфом нуля системы отсчета.

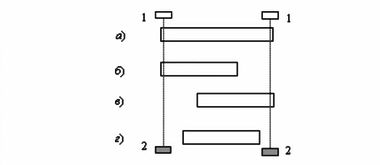
Рис. 8.4. При движении стержня мы будем иметь
различное положение сокращенного стержня.

Пусть покоящийся стержень имеет такую длину, которую едва бы хватило для закрытия фотодатчиков 2 от лучей источников 1 (а). Тогда при движении стержня мы будем иметь различное положение сокращенного стержня: все будет зависеть от положения нулевой отметки системы координат, связанной с нашим стержнем. Поэтому на определенный момент времени может получиться так, что окажется закрытым левый фотодатчик (б), правый (в) или оба датчика окажутся освещенными источниками света (г).

Дрейфом нуля системы отсчета объясняется и известный парадокс зажженной лампочки. На рис. 8.1 показаны следующие варианты

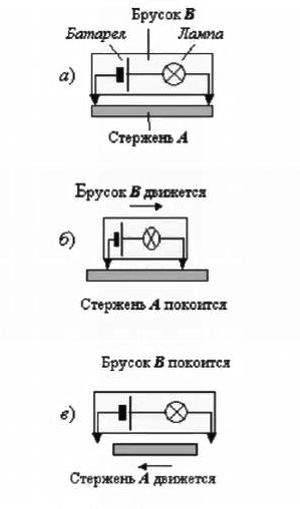
Рис. 8.1. Парадокс зажженной лампочки.
Что произойдет — вспыхнет или не вспыхнет лампочка.

Все элементы электрической цепи находятся в покое: лампочка горит, так как цепь замкнута (а). Из-за быстрого перемещения бруска В расстояние между контактами для наблюдателя А сократится, но лампочка на мгновение вспыхнет, так как цепь на некоторое время окажется замкнутой (б). При быстром движении проводящего стержня А для наблюдателя В цепь окажется постоянно разомкнутой и лампочка никогда не вспыхнет (в). Согласно принципу относительности, два последних случая — (б) и (в) — тождественны. Вопрос: что произойдет в действительности — вспыхнет или не вспыхнет лампочка — вот парадокс?

Таким образом, парадоксы распиленной линейки и зажженной лампочки доказывают, что кинематическое сокращение длины движущихся тел происходить не может, так как поступательное перемещение координатных систем по Галилею не имеет ничего общего с вращательным движением координатных систем по Лоренцу.

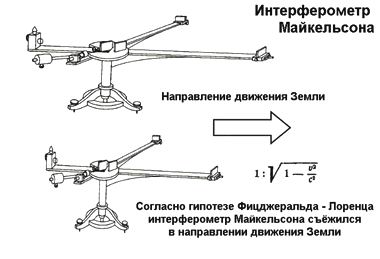
Сегодняшних школьников учат, что интерферометр Майкельсона,
согласно гипотезе Фицджеральд – Лоренца, испытывает сжатие
в направлении движения Земли.

Сегодняшних школьников учат, что интерферометр Майкельсона, согласно гипотезе Фицджеральда – Лоренца, испытывает сжатие в направлении движения Земли, поэтому, дескать, не происходит сдвиг интерференционных полос. Но тут же возникает недоуменный вопрос. Так как Майкельсон во время проведения опыта находился в движущейся координатной системе прибора K', то ни он, ни Лоренц с Фицджеральдом, ни кто-либо другой живущей на Земли не могли зафиксировать сжатие интерферометра.

Как теоретик превращается в обманщика.

Те, кто сейчас говорит о гипотезе сокращения длины, реально превращаются в обманщиков, поскольку путают объектного наблюдателя — Майкельсона — с метанаблюдателями — Лоренцем и Фицджеральдом. На первых порах, когда теория относительности еще не сформировалась, Лоренц и Фицджеральд ничего не говорили о замедлении времени. Сегодня, рассказывая школьникам о гипотезе сокращения длины, учителя обязаны что-то говорить об одновременном замедлении времени. Но этого, к сожалению, не происходит, поскольку они самостоятельно не в силах выбраться из релятивистских спекуляций.

Радиолокационный метод.

Помимо представленных парадоксов нами были найдены математические ошибки во множестве других разделах релятивистской физики. Так, например, Макс Борн, глядя на Германа Минковского, попытался вывести формулы сокращения длины и замедления времени геометрическим путем (см. Радиолокационный метод). Его способ не сделался популярным, как диаграмма Минковского, поскольку Борн допустил еще больше ошибок, чем Минковский. Впрочем, источник ошибок для обоих авторов был один — это подгонка всех геометрических построений под "гипотезу Фицджеральда и Лоренца" о сокращении длины. Это амбициозная цель с самого начала была обречена на провал.

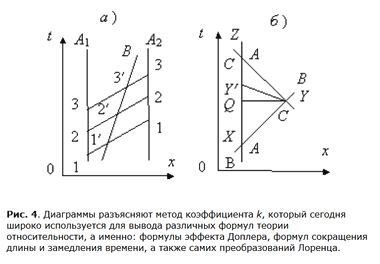
Диаграммы разъясняют метод коэффициента k.

Борн вместе Бомом, Бонди и Ходсбэри принимал участие в разработке радиолокационного метода или метода коэффициента k, который широко использовался для вывода различных формул теории относительности, в том числе, формулы доплеровского эффекта, формул сокращения длины и замедления времени, да и самих преобразований Лоренца. По этой методики авторы ухитрились вывести, например, релятивистскую формулу для эффекта Доплера — вот в таком виде якобы подтвержденную экспериментом.

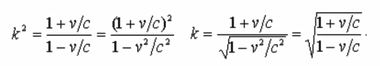
Ошибки этого метода обнаруживаются просто: путем подстановки конкретных числовых данных. Эти ошибки неизбежны, поскольку все авторы метода уверовали, будто штрихованные оси сокращались на величину релятивистского радикала. Откуда взялась эта их вера, геометрически ничем не подтвержденная. Коротенько напомним основные вехи релятивистского наваждения.

Лоренцевы преобразования возникли из ложного толкования эксперимента Майкельсона — Морли. Физики конца 19-го века, не умея объяснить результаты опыта — а мы их объяснили в 1-й части нашего фильма — приняли гипотезу Фицджеральда — Лоренца, которая в умах релятивистов быстро приобрела статус догмы. Согласно их абсурдной теории оптический прибор, используемый Майкельсоном, уменьшил свои размеры в направлении движения Земли. Поскольку в приборе использовались световые сигналы, т.е. электромагнитное излучение, то ключ к разгадке, они посчитали кроется в уравнениях Максвелла.

Начали искать некие преобразования координатных систем, которые бы оставляли эти уравнения в неизменном виде, говорят, в инвариантном виде. Таким образом, релятивисты рассчитывали распространить принцип относительности, справедливый для классической механики, на электромагнитную сферу. Преобразования Галилея оставляют четыре закона Ньютона в неизменном виде; теперь появились преобразования Лоренца, оставляющие четыре закона Максвелла тоже в неизменном (инвариантном) виде. За счет спекуляций на условии предельного перехода релятивисты стали утверждать, будто бы преобразования Галилея являются частным случаем общих преобразований Лоренца.

В отношении инвариантности уравнений Максвелла имеется серьезное возражение. Дело в том, что Фарадей и Максвелл, разрабатывая теорию электромагнетизма, опирался на эфир в виде некой гидродинамической модели. Поэтому из уравнений Максвелла легко выводится волновое уравнение, справедливое для воды, воздуха и прочих сплошных сред (см. Инвариантность волнового уравнения).

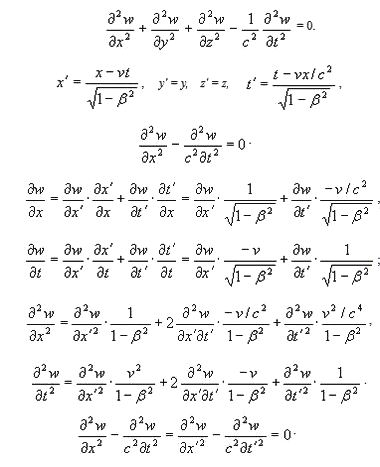
Верно, что Лоренц вывел преобразования, названные Пуанкаре "лоренцевыми", из области электромагнетизма, которая, однако, в то время целиком покоилась на эфирных представлениях. Поскольку Лоренцевы преобразования, оставляющие уравнения Максвелла и выведенное из них волновое уравнение в инвариантном, т.е. неизменном, виде, возникает законный вопрос: а как быть с медленными акустическими волнами, распространяющимися, например, в воде и воздухе? Что скажут релятивисты, в частности, по вопросу предельного перехода. Ведь для акустических волн фигурирует, разумеется, не умопомрачительная скорость света, а вполне себе умеренная скорость звука где-нибудь в воде или воздухе.

Убийственный аргумент. Релятивист должен застрелиться,
когда обнаружит неинвариантность уравнений теплопроводности и
диффузии. Ведь они не подчиняются принципу относительности Эйнштейна.

Но самым убийственным аргументом для релятивистов является не этот. Они напрочь забывают, что преобразования Лоренца оставляют в инвариантном виде исключительно волновые уравнения — какую бы природу они не носила — электромагнитную или акустическую — но они не оставят в неизменном (инвариантном) виде все прочие уравнения механики.

Посмотрите, так выглядит волновое уравнение, а так выглядит уравнение теплопроводности и диффузии, где вместо параметра 1/с2 стоит параметр 1/с где, c — постоянная теплопроводности или диффузии. Таким образом, невозможно говорить о каких-то универсальных преобразованиях, которые бы оставляли инвариантными все без исключения дифференциальные уравнения. Само такое требование является математически некорректным.

См. фильм с этим текстом

http://youtu.be/BBU2sF7dy1M