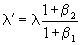Критика теории относительности

О.Е. Акимов

11. Радиолокационный метод

– I –

Его еще называют методом коэффициента k. Идея возникла при решении парадокса двух братьев-близнецов путем введения еще одного брата-космонавта. Начало этому методу положили Бонди и Холсбэри; в изложении Борна он предстал особенно в выгодном свете; Бом сделался неутомимым поборником и усердным пропагандистом его; сейчас он вошел практически во все более или менее полные учебники по теории относительности. Заявленная тема тесно связана с ранее рассмотренными вопросами Ортогональные и гиперболические преобразования и Масштаб осей при гиперболическом повороте (см. также Слайд № 7 из Введения в конструктивную физику).

Напомним, существует пассивная и активная форма преобразования координат. Пассивные преобразования отличаются от активных тем, что первые оставляют объект А на месте и поворачивают штрихованные оси координат, вторые оставляют оси на месте, перемещая объект из точки А в точку А' (рис. 1); в этом случае к углу ψ прибавляется угол φ.

Рис. 1. Преобразования координат: пассивное гиперболическое (а), активное гиперболическое (б) и активное ортогональное (в).

В разделе dm2-5i «Дискретной математики» было показано, что любые преобразования на плоскости сводятся к тригонометрическим формулам для суммы двух углов. При гиперболическом повороте будем иметь:

ch(φ + ψ) = chψ chφ + shψ shφ,     sh(φ + ψ) = chψ shφ + shψ chφ.

Выражая значения гиперболических косинусов и синусов через соответствующие отрезки на чертежах, находим преобразования Лоренца в виде:

= ,

= .

где , — нормированные координаты,

— нормировочный, или масштабный, коэффициент.

Релятивисты прекрасно знают, что их масштабный коэффициент, выражающий отношение 1 к не работает на диаграмме Минковского. Однако они предпочитают спекулировать им, т.к. он, по их мнению, согласуется с результатами эксперимента Майкельсона – Морли. В том, что масштабный коэффициент k_n найден нами правильно, легко убедиться на числовом примере.

Пусть точка А (рис. 1a) имеет в системе K координаты (в мм): x = 63, ct = 135, а в K' — x' = 30, ct' = 131. Тогда β = 0,267 и k_n = 0,931. Интервалы в K и K' соответственно равны: s ≈ –14 × 10³ и s' ≈ –16 × 10³. Согласно теории относительности, интервалы равны: s = s', но для получения равенства нужно s' еще умножить на k²_n, так как истинное равенство интервалов выглядит следующим образом:

s = (x)² – (ct)² = k²_n[(x')² – (ct')²] = k²_ns'

Гиперболические преобразования (или лоренцевы), а также инвариантность квадратичной формы будут выполняться только после поправки на масштабный коэффициента k_n , который «сжимает» масштабные единицы обеих осей штрихованной системы K' до нужной величины. Для нашей конкретной точки А это сжатие будет равно:

x'_n = k_nx' = 0,931 × 30 = 27,9 мм,       ct'_n = k_nct' = 0,931 × 131 = 122,8 мм.

А это как раз и означает, что между «эталонами длины и времени» (релятивистский термин, лучше сказать масштабными единицами) системы K и K' выполняются неравенства: Δx > Δx'_n и Δt > Δt'_n , т.е. происходит «сжатия» обеих штрихованных осей, так как масштабный коэффициент k_n < 1. Однако отсюда вовсе не следует, что в реальном физическом мире сокращаются пространство и время.

Нельзя не заметить, что в получении преобразований Лоренца, соответствующих диаграмме Минковского, был использован искусственный прием: умножение числителя и знаменателя преобразований

        и        

на величину .

Для этих преобразований (их нельзя уже назвать Лоренцевыми или гиперболическими) не нужно вводить никаких масштабных коэффициентов. Для того чтобы найти значения координат x и ct, нужно просто подставить значения x' и ct' в два последних выражения.

Таким образом, диаграмма Минковского, вообще говоря, не удовлетворяет преобразованиям Лоренца. Но их соответствия можно добиться путем введения найденного выше масштабного коэффициента «сжатия» ( k_n ), который определяется намного проще, если из последних преобразований составить квадратичную форму (x)² – (ct)².

Обращаем особое внимание на то, что преобразования координат при ортогональном повороте (см. раздел dm2-5h) отличаются от выписанных преобразований только знаком перед членом βct'. Все вышеприведенные громоздкие выкладки воспроизводят релятивистскую логику рассуждений, традиционно связанную с диаграммой Минковского и преобразованиями Лоренца. Но фактически эти рассуждения лишние, так как рис. 1а непосредственно подсказывает нам простейшее решение.

Вот оно: чтобы получить преобразования, соответствующие диаграмме Минковского, нужно в ортогональных преобразованиях знак минус перед членом βct' заменить плюсом. В этом случае координаты в системе K любой точки А — неважно лежит она на гиперболе или нет — можно найти по координатам системы K', если воспользоваться слегка модернизированными (т.е. учитывающими знак перед βct') формулами поворота декартовых систем отсчета.

Как вурдалак ненавидит дневной свет и с появлением первых лучей солнца пытается укрыться в своем темном логове, так релятивист не любит ясных геометрических образов и пытается спрятаться от них за частоколом своих спекулятивных формул. Ложное представление о лоренцевом сокращении длины и замедлении времени появилось до построения графических чертежей, где только-то и можно было обнаружить факт «сокращения» или «удлинения» масштабных единиц, если таковые имели бы место. Это и понятно релятивисты тем и отличаются от конструктивистов, что не умеют мыслить пространственными образами и очень презрительно относятся к любым геометрическим построениям.

Хорошо известно, что сам Эйнштейн никогда ими не занимался и в четырехтомном собрании его трудов вы не найдете каких-либо чертежей. Даже диаграммам Минковского он, очевидно, не слишком доверял; единственное, о чем он считал необходимым сообщить практически во всех случаях повторного изложения им специальной теории относительности (а наиболее ясным изложением ее, по-видимому, нужно считать статью в энциклопедии «Физика» 1915 года), так это о мнимости временной оси.

«...Минковский исходил из того, — писал Эйнштейн, — что "временная координата будет входить в основные уравнения теории относительности точно таким же образом, как и пространственные координаты, если вместо t ввести пропорциональную этой величине мнимую переменную ict. Благодаря этому, уравнения теории относительности становятся уравнениями в четырехмерном пространстве; при этом формальные свойства этого четырехмерного мира отличаются от формальных свойств пространства евклидовой геометрии только числом измерений» [7, с. 421].

У Минковского имеется две работы с интересующим нас вопросом. В более ранней работе он не рассматривал временную ось как мнимую, стремясь чисто геометрическим путем получить отношение 1 к . Это доказательство Минковский провел совершенно неудовлетворительно. Работа, о которой идет речь, была написана на основе доклада, прочитанного Минковским 21 сентября 1908 года в Кёльне.

Выступление начиналось с вдохновенных слов, которые релятивисты часто цитируют. «Милостивые господа! — обратился Минковский к своим слушателям. — Воззрения на пространство и время, которые я намерен перед вами развить, возникли на экспериментально-физической основе. В этом их сила. Их тенденция радикальна. Отныне пространство само по себе и время само по себе должны обратиться в фикции и лишь некоторый вид соединения обоих должен еще сохранить самостоятельность» [1, c. 167].

Однако его путаное обоснование преобразований Лоренца никто больше не решился повторить, хотя вычерченный им чертеж, напоминающий рис. 1а, стали называть диаграммой Минковского и считать геометрическим доказательством правильности отношения 1 к . Макс Борн пытался идти своим путем, но у него тоже ничего не вышло. Проследим, как он выводил этот релятивистский масштабный коэффициент.

Пусть, предположил Борн, единица времени в покоящейся системе K равна T, а в движущейся системе K' равна T '. Длительность t' получается в результате проекции единичной длительности K покоящейся системы на временную ось движущейся системы, период времени t является проекцией единицы времени T ' движущейся системы на ось времени покоящейся системы (рис. 2). Принцип относительности требует выполнения непременного условия: t' / T ' = t / T, что определит положение точки T '.

Рис. 2. К выводу соотношения между масштабными единицами системы K и системы K', предложенное М. Борном [2].

Введя точку T ", будем иметь два прямоугольных треугольника с тангенсом tg φ = v/c и нижеследующими фактическими равенствами, получающимися непосредственно из чертежа:

,    ,    ,    .

Из двух последних равенств находим соотношение между T ' и t, а из треугольника 0t'T – выражение, связывающее T и t' :

,    .

Подставляя эти два выражения в пропорцию t' / T' = t / T , Борн получает известные соотношения для замедления эталонов времени:

,    .

Поскольку ситуация с пространственными осями аналогичная, Борн выписывает пару формул для сокращения длины:

,    .

Эта геометрическая интерпретация ошибочна, так как Борн пошел на незаконную операцию «расщепления» события A на два различных события — A₁ и A₂, тем самым удвоив число необходимых масштабных единиц: x, x', X, X', t, t', T, T '. Эту ошибку не сразу можно заметить, так как Борн вместо одного чертежа (рис. 2) вычертил три, причем выбрал для них не самую удачную систему обозначений [2, с. 281 – 285]. Если же все его чертежи свести в один и использовать более удобную систему обозначенияй координат, то ошибки предложенного им способа обоснования масштабного отношения 1 к быстро обнаружится.

Тем не менее, его попытку найти соотношение, связывающее T ' и t, следует назвать реалистичной. Борн всё-таки использовал реальные отрезки длины, а не виртуальные, как это делают нынешние релятивисты. Поэтому в его равенстве фигурирует выведенный нами масштабный коэффициент k_n :

.

Выше мы получили формулу, которая связывала штрихованный и нештрихованный параметры иначе. Сравните наше, ранее найденное выражение, и Борна:

,    .

Для того, чтобы проиллюстрировать виртуальный способ доказательства масштабного отношения 1 к , являющийся чисто спекулятивным, воспользуемся учебником В.Г. Левича [3].

«Если обозначить через φ угол поворота, — пишет Левич, — то ... можно написать связь между исходными координатами (x, τ) и преобразованными координатами (x', τ'):

x = x' cos φ – τ' sin φ,       (10,11)      τ = τ' cos φ + x' sin φ.       (10,12)

Рис. 3. Эти рисунки в точности соответствуют рис. 22 и рис. 23 «Курса теоретической физики» В.Г. Левича [3].

Угол поворота φ должен, очевидно, быть различным при разных значениях скорости v. Напишем преобразования (10,11) и (10,12) для начала координат системы K', т.е. точки x' = 0. Имеем x = – τ' sin φ,    τ = τ' cos φ.

Разделив верхнее выражение на нижнее, получаем tg φ = – x / τ, или

tg φ = ix/ct = iv/c,       (10,13)

где v — скорость равномерного движения начала координат системы K' (точка x' = 0) относительно системы координат K. Из равенства (10,13) можно без труда найти значения величин sin φ и cos φ, входящих в формулы (10,11) и (10,12):

,    .

При этом

,     (10,13) .    (10,14)

Переходя от τ к времени t, мы видим, что формулы (10,14) и (10,15) совпадают с преобразованиями Лоренца.

Нелишне подчеркнуть условный характер графического изображения преобразований Лоренца. Угол поворота на рис. 3а является мнимым. Разумеется, изобразить поворот на мнимый угол мы не можем. Достоинства и недостатки графического представления преобразования Лоренца ясно видны из нижеследующего рассмотрения. Пусть в системе K' в некоторой точке x' покоятся часы. Это физическое событие в момент времени τ'₁ изобразится первой точкой, в момент времени τ'₂ — второй точкой на оси τ'. Промежуток времени Δτ' равен длине участка от точки 1 до точки 2. При переходе к системе K (повороте на угол φ) отрезок Δτ' переходит в отрезок Δτ на оси τ. Мы ясно видим, что бессмысленно говорить о том, какая система отсчета является более правильной и какой из промежутков времени, Δτ' или Δτ, является истинным промежутком времени между двумя физическими событиями.

Недостатком геометрического рассмотрения является то, что взаимоотношение между Δτ' и Δτ на чертеже является обратным истинному: на чертеже Δτ меньше, чем Δτ', в действительности же он больше в отношении 1 к . Искажение возникает потому, что мы не можем изобразить на рисунке мнимое значение угла φ и заменяем его вещественным углом.

Аналогичную геометрическую интерпретацию допускают преобразования длины (рис. 3б)...» [3, с. 215 – 217].

По законам математического жанра всякая геометрическая интерпретация призвана дать человеку наглядный графический образ каких-то аналитических выражений. В данном случае ее функция свелась к обратному — к полной дезориентации наших представлений. Левич сослался на невозможность нахождения тригонометрических функций от мнимого значения угла φ. Такая отговорка совершенно здесь неоправданна, поскольку указанные величины отображаются в математике гиперболическими функциями, в частности: cos iφ = ch φ > 1. Физик Левич мог о них ничего не знать, но математикам их геометрическое представление хорошо известно. Предшествующий окончательным формулам (10,14) и (10,15) текст из книги можно безболезненно выбросить, так как они непосредственно получаются из прямых преобразований Лоренца для x и t : формула (10,14) вытекает из преобразований для x путем замены

,

формула (10, 15) — из преобразований для t путем умножения обеих частей на ic. Если кто-то рассчитывал в результате этих простейших манипуляций постигнуть геометрическую сущность преобразований Лоренца, то он в этом глубоко заблуждается.

Однако нас сейчас не особенно интересуют чьи-либо пробелы в математических знаниях, мы хотели обратить внимание читателя на постановку и решение проблемы в принципе. Спрашивается, зачем вычерчивать рисунок, на котором изображен результат «обратный истинному»? Как понимать «условный характер графического изображения»? Почему, собственно, мы должны брать на веру то, что в «действительности» все будет ровно наоборот? Если возникли «искажения», значит, ни о каком решении задачи не может быть и речи. Любой, уважающий себя ученый, а тем более преподаватель обязан нести людям нечто завершенное, истинное. Данное же изложение материала только дискредитирует математику в глазах молодых людей, запутывает студентов и прививает им дурной вкус из-за небрежных доказательств.

Всякий непредвзято мыслящий студент или даже школьник в приведенных Левичем рис. 3 прекрасно увидит традиционный ортогональный поворот одной декартовой системы отсчета относительно другой. Все выделенные там отрезки соотносятся между собой посредством обыкновенных тригонометрических функций; искать среди них «сокращенные» или «удлиненные» по Эйнштейну отрезки бессмысленно. Когда кто-нибудь говорит вам, что преобразования Лоренца невозможно геометрически интерпретировать, так как появляется мнимая единица, или что для изображения комплексных величин требуется псевдоплоскость, гиперпространство и пр., которые и вообразить-то нельзя, знайте — он вас обманывает. Не бойтесь, с появлением символа « i » рядом с символами « ct » ваш чертеж не исчезнет с листа бумаги; на чистом листе бумаги можно изображать рисунки как евклидовой, так и неевклидовой геометрии.

Здесь важно помнить одно: геометрический чертеж «не знает», как вы обозначили отрезок длины — x, t, ct, ict, x', t', ct', ict'. Главным для геометрии является реальное соотношения длин и реальные, т.е. конкретно отложенные на бумаге, углы поворотов осей. Понятие мнимой единицы не является чем-то таким, с чем математики не знают, как обращаться. Все спекуляции с псевдоевклидовой геометрии идут из одного источника: страстного желания доказать несуществующее в геометрии масштабное отношение 1 к . Ради этого авторы идут на чудовищные преступления, причем дело касается самых азов элементарной математики, которую изучают школьники.

Редко кто из релятивистов соглашается со спекуляциями своих товарищей. Минковский предложил вывод отношения 1 к , с которым не согласился Борн; Борн предложил свое доказательство, с которым не согласился Левич; с последним, в свою очередь, не согласились другие авторы. Таким образом, каждый релятивист изобретает на своем рабочем месте что-нибудь свое, отличное от других. Однако же выискивать у релятивистов ошибки в их геометрических интерпретациях преобразований Лоренца не очень интересно, поскольку все они не отличаются большим разнообразием и примерно схожи с приведенной выше интерпретацией из учебника В.Г. Левича.

Возьмите, к примеру, курс по специальной теории относительности, написанный В.А. Угаровым, который еще в 40-х годах прошлого века вместе с В.Л. Гинзбургом интенсивно пропагандировал теорию относительности. В его курсе вы прочтете похожие слова, сказанные Левичем: «Не следует забывать, однако, что изображение псевдоевклидовой плоскости на евклидовой условно» [4, с. 123]. Чтобы показать, что чистый лист бумаги образует евклидову плоскость, автор вычерчивает прямоугольный треугольник, стороны которого удовлетворяют теореме Пифагора: AB² = BC² + AC², и добавляет: мы же не в состоянии изобразить «псевдоевклидову плоскость на листе бумаги», где бы выполнялась «псевдопифагорова теорема»: AB² = BC² – AC². Гипнотическое действие релятивистской физики было столь оглушительным, что даже исключительно математические книжки, например «Высшая геометрия» Н.В. Ефимова и «Риманова геометрия и тензорный анализ» П.К. Рашевского, лишились наиважнейших формул пересчета масштабных единиц из ортогональной системы в гиперболическую и наоборот.

– II –

Проблемы, описанные в предыдущей части, более или менее знакомы нашему читателю по предыдущим разделам. Теперь давайте посмотрим, как ложное отношение 1 к между единицами измерения в ортогональной и гиперболической системами координат отразилась на выводе наиважнейших формул в рамках радиолокационного или метода коэффициента k, который широко используется для вывода различных формул теории относительности, в том числе, формулы доплеровского эффекта, формул сокращения длины и замедления времени и самих преобразований Лоренца. С этой целью обратимся к статье Макса Борна [5], в которой комментируются идеи, предложенные Бонди и Холсбэри.

«В работе [Бонди], — пишет Борн, — рассматривается одномерное движение и используются (x, t) диаграммы. Пусть A₁ и A₂ — два наблюдателя, покоящиеся в инерциальной системе отсчета; их мировые линии являются двумя параллельными прямыми (рис. 4a). Оба имеют физически одинаковые часы. Испускаемые наблюдателем A₁ световые сигналы через равные промежутки времени t будут приниматься наблюдателем A₂ тоже через равные промежутки времени t.

Пусть наблюдатель B движется между A₁ и A₂ в направлении от A₁ к A₂ со скоростью v, меньше, чем скорость света c. Наблюдатель B несет часы, физически идентичные с часами наблюдателей A₁ и A₂. Излученные A₁ в моменты времени 1, 2, 3, ... (по часам A₁) световые сигналы достигают наблюдателя B соответственно в моменты времени 1', 2', 3', ... (по часам B ). Из-за доплер-эффекта (который является опытным фактом) интервал t' по часам B не будет равен соответствующему интервалу t по часам A, а t' = kt,    (4)

где k — функция относительной скорости v, причем k > 1.

Согласно принципу относительности, можно рассматривать B покоящимися, а A₁ и A₂ — движущимися. Если B излучает световые сигналы точно в моменты 1, 2, 3, ..., соответствующие моментам прихода сигналов из A₁ в B, то сигналы, посылаемые наблюдателем B в направлении A₂, будут идентичны сигналам, посылаемым непосредственно из A₁ в A₂. Таким образом, имеет место то же самое соотношение t' = kt, которое теперь следует читать t = t'/ k. Это означает, что доплеровский эффект при сближении окажется обратным доплеровскому эффекту при удалении.

Рис. 4. Диаграммы разъясняют метод коэффициента k, который сегодня широко используется для вывода различных формул теории относительности, а именно: формулы эффекта Доплера, формул сокращения длины и замедления времени, а также самих преобразований оренца.

После этой небольшой подготовки Бонди не сразу переходит к рассмотрению ускоренного движения B, а заменяет его, следуя Холсбэри, равномерным движением (рис. 4 б). Наблюдатель A покоится в инерциальной системе. Движущийся с постоянной скоростью v в этой системе наблюдатель B встречается с наблюдателем A в точке X мировой линии A ; в этот момент оба они сверяют свои часы. Третий наблюдатель C движется тоже с постоянной скоростью v в инерциальной системе A и встречается с наблюдателем B в точке Y мировой линии B и затем — с A в точке Z мировой линии A. Проекция Q точки Y на мировую линию A делит отрезок XZ на две равные части.

В момент встречи Y наблюдателей B и C испускается световой сигнал, который доходит до мировой линии A в момент Y'. Очевидно,

XQ = QZ = t₀,    QY = vt₀,    QY' = QY/C = vt₀/c,

а также

XY' = t₀(1 + v/c),    Y'Z = t₀(1 – v/c).    (5)

С другой стороны, XY' и Y'Z являются теми отрезками мировой линии A , которые принимают световые сигналы, испущенные на мировой линии B между моментами X и Y или на мировой линии C между моментами Y и Z. Пусть t₁ — интервал времени, измеренный наблюдателем B при движении между точками X и Y . Так как в первом случае имеем взаимное удаление наблюдателей B и A , а во втором — взаимное сближение наблюдателей C и A, то, в соответствии со сказанным выше,

XY' = kt₁ ,    Y'Z = t₁/ k,    (6)

Сравним (5) и (6)

kt₁ = t₀(1 + v/c),    t₁/k = t₀(1 – v/c).    (7)

Разделив первое соотношение (7) на второе, получаем

   .

Это известная релятивистская формула эффекта Доплера, подтвержденная экспериментом.

С другой стороны, умножая соотношения (7) друг на друга и извлекая корень, получаем известную формулу сокращения времени » [5].

Из Ошибочности релятивистской формулы Доплера мы уже знаем о выполнении приближенного равенства:

, .

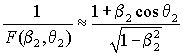При θ₂ = 0º это выражение принимает значение полученного в статье Борна коэффициента k.

Этот коэффициент k или, что одно и то же, релятивистскую формулу Доплера можно получить иначе. Для этого нужно вспомнить, что сигнализация между наблюдателями A, B и C осуществляется лучами света, скорость которого в системах отсчета K и K' одинаковая, т.е. x/t = x'/t' = c или x = ct, x' = ct'. Теперь возьмите преобразования Лоренца, скажем, для x, и подставьте в него это условие: вы немедленно получите преобразования Лоренца для t, и наоборот. Из преобразования для x можно исключить компонент времени, а из преобразования для t — компонент пространства, тогда одноименные координаты систем K и K' будут связаны как раз через коэффициент k :

:    =    t = kt';

:    =    x = kx'.

Геометрический смысл первого условия: x/t = x'/t' = c, такой же, как и второго: x/ x' = t /t' = k, — оба условия задают биссектрисы секторов, ограниченных соответствующими осями. Первое условие автоматически влечет за собой второе, и наоборот. Никакого физического смысла коэффициент k, конечно, не несет (его причастность к эффекту Доплера нужно перепроверять — релятивистам здесь доверять нельзя), а вот геометрическое содержание всех этих манипуляций мы сейчас подробно проанализируем. Далее, произведя точное геометрическое построение (идея построения взята из книги Бома [6]), мы убедимся, что именно реальная картина геометрических размеров отрезков не такова, как она представлялась Борну, Бому, Угарову и прочим релятивистам.

На рис. 5 изображены две системы отчета K и K', в которых точка A проецируется двумя способами. Из чертежа имеем:

x = (ct₀ + x₀),    ct = (ct₀ – x₀);   

x' = (ct'₀ + x'₀),    ct' = (ct'₀ –x'₀);   

ct₁ = –x₀,    ct'₁ = –x'₀.

Напомним, что если декартову систему координат, в которой задано уравнение гиперболы y² – x² = 1, развернуть на угол 45º, то уравнение гиперболы изменится на уравнение: XY = 1. Новые координаты X и Y некоторой точки A, взятой на гиперболе, будут пропорциональны сумме y + x и разности y – x старых координат (развернутую на 45º координатную систему изображать не будем). Точку A можно проецировать на старые координаты x, y, при этом коэффициент , получающийся от cos 45º и sin 45º, необходимо умножать еще на один такой же коэффициент, в результате чего получится уже множитель 1/2. Линия, наклон которой равен 45º, соответствует скорости света (биссектрисы систем K и K' ). Поэтому, когда Борн говорит о посылке светового сигнала из точки Y в точку Y' (рис. 4б), то на самом деле эта процедура означает проецирование точки Y на ось ct (линия AA), аналогично точка Y' проецируется на ось ct' (линия BB).

Рис. 5. Заинтересованным читателям рекомендуется вычертить данный чертеж и самим произвести все необходимые измерения отрезков. Так они смогут лучше понять ошибку, допущенную авторами и комментаторами метода коэффициента k — Борна, Бонди и Бома.

Установим связь между координатами штрихованной и нештрихованной систем для этой новой формы проецирования события A. В связи с этим введем два пересчетных коэффициента k' и k". Если коэффициенты окажутся одинаковыми, то их можно будет впоследствии принять за одну величину. Итак, полагаем ct₀ = k'ct'₀ и x₀ = x'₀/k". Подстановка этих равенств в предыдущие уравнения позволяет найти преобразования Лоренца:

x = (ct₀ + x₀) = (k'ct'₀ – x'₀/k") =

ct = (ct₀ – x₀) = (k'ct'₀ + x'₀/k") =

Складывая и вычитая эти равенства, а также помня, что ct'₀ = ct' + x', x'₀ = ct' – x', находим, что оба введенных коэффициента k' и k" равны k, который чудесным образом совпал с величиной доплер-эффекта:

k = k' = = = = k".

Истинный конструктивист никогда не поверит путаным рассуждениям релятивистов, пока сам не выполнит все необходимые построения и вычисления. Авторы метода установили, казалось бы, реальные геометрические отношения на своем чертеже (рис. 5). Однако мы уже заранее знаем, что в их суждения вкралась ошибка, поскольку они не учли истинного масштабного коэффициента k_n. Если учесть его влияние на чертеж и произвести несложные вычисления, то никакого равенства коэффициентов k' и k" мы не получим — судите сами:

k' = k / k_n = ct₀ / ct'₀ = ,

k" = k × k_n = x'₀ / x₀ = ,

Тщательное вычерчивание чертежа (рис. 5) с конкретными координатами (в мм):

x = 105, ct = 177, x' = 77, ct' = 165, x₀ = 70, ct₀ = 280, x'₀ = 87, ct'₀ = 242,

позволяет найти параметр β = 0,176, истинный масштабный коэффициент k_n = 0,968 и все введенные нами коэффициенты k = 1,195, k' = 1,158, k" = 1,243. Как видим, k' ≠ k"

А почему, собственно, коэффициенты k' и k" должны быть равны? Ведь в классической физике движения источника и приемника строго различаются. В итоге мы имеем восемь вариантов, которые показаны в следующей таблице:

Состояния приемни- ка A и источника i	Принимаемая длина волны λ'
A и i сближаются: A – движется, i – покоится
A и i сближаются: A – покоится, i – движется
A и i удаляются: A – движется, i – покоится
A и i удаляются: A – покоится, i – движется
A и i оба движутся навстречу друг ругу на сближение
A и i оба движутся в противоположные стороны на удаление
A и i оба движутся в положительном направлении оси x
A и i оба движутся в отрицательном направлении оси x

У релятивистов эта таблица из восьми формул сводится к одному-единственному выражению, с помощью которого ровным счетом ничего нельзя установить. Возьмем, например, относительное сближение солнечной системы и какой-нибудь далекой звезды, для которой зафиксировано фиолетовое смещение спектральных линий. Нельзя определенно сказать: то ли мы приближается к звезде, то ли она приближается к нам, то ли она и мы двигаемся навстречу друг другу, то ли мы летим от звезды, а она нас догоняет, то ли наоборот. Аналогичная картина с удалением источника и приемника, когда наблюдается красное смещение. Причем обе задачи, на сближение и удаление, очевидно, решаются путем смены знака перед разностью скоростей источника и приемника, поскольку для использования обратной формулы нет достаточных оснований. Теперь задайтесь вопросом, как эту чудесную теорию можно проверить экспериментально, когда она годится для всех возможных вариантов? Так как в первом приближении 1/(1 – β) ≈ 1 + β, то в эксперименте, наверное, не всегда можно отчетливо различить движение приемника и источника.

Метод коэффициента k сильно запутан и его ошибки не слишком бросаются в глаза неспециалистам. Но возьмите такие вопиющие ошибки, как предельный переход от преобразований Лоренца к преобразованиям Галилея, который осуществляют релятивисты. Эта тема изложена в разделе dm2-5f «Дискретной математики», до которого, однако, не у всех физиков доходят руки. Напомним его суть.

Считается, что преобразования Лоренца:

,    

перейдут в преобразования Галилея: x = x' + vt' , t' = t, если к первой паре формул применить предельный переход: v/c → 0. Нормальный математик сразу же заметит здесь ошибку: в числителе самого первого выражения переменная v оказалась без необходимой в этом случае константы c. Ясно, что в такой форме преобразования Лоренца использовать нельзя; их нужно записывать через параметр β:

,     ,

Тогда при условии β → 0 или φ → 0 гиперболические функции ведут себя так, как показано в таблице:

β	0,99	0,80	0,70	0,60	0,50	0,40	0,30	0,20	0,10	0,00
ch φ	7,089	1,667	1,250	1,091	1,048	1,021	1,0050	1,0012	1,0001	1,0000
sh φ	7,018	1,333	0,750	0,436	0,315	0,204	0,1005	0,0501	0,0100	0,0000

Отсюда преобразования Лоренца в случае предельного перехода параметра β → 0 трансформируются в единственно возможные равенства: x = x', ct = ct'. Таким образом, никакого перехода от физики больших скоростей к физике малых скоростей не существует. Утверждение о некой преемственности двух физик является ложным. Никто в мире не сможет указать вам, где заканчивается классическая физика и начинается релятивистская. Никакой границы между ними нет, так как преобразования Лоренца не отражают поступательного движения физических тел.

Теперь спросите себя, разве современной науке неизвестно, как ведут себя гиперболический косинус и синус при условии φ → 0? Прекрасно известно:

ch φ = → 1,          sh φ = → 0.

Тогда, почему никто не торопится исправлять эту чудовищную ошибку в учебниках и справочниках по физике? Да потому что сегодняшние физики абсолютно не заинтересованы в установлении истины. Исправление этой ошибки заставит их обратить внимание на сотню других ошибок. В результате можно прийти к отрицанию всего схоластического фундамента физики, на что у наших генералов науки никогда не хватит духа.

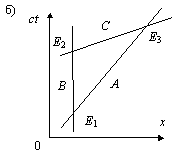
В заключение данного раздела напомним читателям, что решение парадокса часов с помощью трех наблюдателей, использованных Холсбэри и его последователями, — ошибочно. Об этом рассказывалось в разделе Парадоксы времени, откуда взята следующая картинка (рис. 6).

Рис. 6. На диаграмме (а) показаны три брата-близнеца: домосед А, летящий от Земли В и летящий к Земле С. Холсбэри доказал, что брат А окажется старше двух других. Однако этот автор не догадался вычертить диаграмму (б), которая продиктована принципом относительности движения, иначе бы он увидел, что все его рассуждения о старшинстве брата А нужно отнести и к двум другим братьям.

С учетом этого обстоятельства все чертежи, изображенные на рис. 4 и рис. 5, нужно пересматривать. Естественно, что формулы, полученные из новых рисунков, будут противоречить старым. Это противоречие лишний раз подтвердит, что радиолокационный метод или метод коэффициента k никуда не годится. Угаров, рассказав об этом методе, написал: «…Игра в световые зайчики в конечном счете позволяет получить основные следствия постулатов Эйнштейна» [4, с. 99]. И это действительно так: «изящный метод» коэффициента k был сначала придуман для разрешения только парадокса часов по схеме трех наблюдателей, предложенной Холсбэри, но потом он оказался столь дивным инструментом для спекуляций, что релятивисты стали использовать его для получения практически всех формул своей замечательной концепции.

Одной из провозглашенных нами целей является анализ спекулятивного мышления релятивистов. Задача состоит не только в том, чтобы дать верную формулу взамен ошибочной, как это было сделано в данном разделе, но и раскрыть схоластическую природу методов доказательства, принятых в релятивистской физике. Конечно, немало было уже сказано в этом отношении раньше. В частности, говорилось, что одним из основных приемов спекулятивной логики является явное, как это было в первой работе Эйнштейна 1905 года, или неявное введение абсолютного пространства метанаблюдателя. В данном разделе приводилась выдержка из учебника Левича, где тот использовал условно-правильные чертежи, в которых отсутствуют истинные геометрические отношения. Этот прием тоже широко используется релятивистами, которые почти никогда не ставят задачи строгой геометрии, доведенные до конкретных числовых значений. Как правило, они ограничиваются приблизительными графическими чертежами, призванными лишь пояснять их путаные рассуждения.

То же самое происходит и с формулами. На примере парадокса штриха было показано, что за словами «сокращение длины» и «замедление времени» на самом деле стоят по паре противоположных формул. Получилось, что релятивизм объектных наблюдателей повлек за собой релятивизм в среде субъектов теории. Пороки релятивизма нигде так себя не проявили, как при решении парадокса часов. На примере этого хорошо известного парадокса можно видеть релятивизм в его более широком смысле, как философию относительного решения физических проблем. Согласно этому спекулятивному мировоззрению, мы имеем столько точек зрения, сколько ученых занимается данной тематикой. Каждый исследователь создает свою индивидуальную теорию или, во всяком случае, имеет свою индивидуальную позицию по тому или иному теоретическому вопросу.

Проблемы с формулами для доплер-эффекта, замедления времени и сокращения длины, которые были рассмотрены нами в других разделах, являются следствием этой двусмысленности. Причем указанная неоднозначность, похоже, мало беспокоит релятивистов, они даже и не пытаются устранить многозначность своих формулировок. Парадокс часов служит этому прекрасным доказательством: сколько людей принималось за его анализ, столько и мнений существует по его разрешению. В течение нескольких десятилетий над этой проблемой бились виднейшие физики планеты. В результате титанических усилий на свет появился метод коэффициента k, который до того запутал простейшую ситуацию с часами и световыми сигналами, что сегодня отыщется немного смельчаков, решившихся на критику этого метода. Мы, однако, решились, что из этого получилось, судить вам, дорогой читатель.

---

1. Минковский Г. Пространство и время / в кн.: Принцип относительности. – М.: Атомиздат, 1973.
2. Борн М. Эйнштейновская теория относительности. – М.: Мир, 1964.
3. Левич В.Г. Курс теоретической физики. Т.1,- М.: Наука, 1962.
4. Угаров В.А. Специальная теория относительности. – М.: Наука, 1977.
5. Борн М. Космические путешественники и парадокс часов. – УФН, т. 59, вып. 1, 1959, с. 105 – 110. Эта же статья в кн.: Размышления и воспоминания физика. – М.: Наука, 1977, с. 126 – 132.
6. Бом Д. Специальная теория относительности. – М.: Мир, 1967, с. 165 – 175.
7. Эйнштейн А. Теория относительности. – СНТ. Т.1. – М.: Наука, 1965.