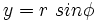Критика теории относительности

Олег Акимов

12. Отклонение лучей света вблизи массивных тел

– I –

Более или менее подробное описание зарождения СТО читатель найдет в разделе Как создавалась специальная теория относительности. Цель данного раздела — проследить ход мыслей Альберта Эйнштейна после опубликования им работы 1905 года «К электродинамике движущихся тел», которая к 1913 году одержала верх над другими конкурирующими теориями электрона, предложенными Лармором (он один из первых получил преобразования Лоренца), Лоренцем и Пуанкаре. В своем анализе развития теории относительности мы намерены уделить внимание не только логике хода рассуждений Эйнштейна, но и экспериментальному обоснованию его идей.

Переход от СТО к ОТО произошел уже в работе 1907 года «О принципе относительности и его следствиях». В пятой части этой работы, которая называется «Принцип относительности и тяготение», в 17-м параграфе, являющимся первым для этой части, рассматривается вопрос эквивалентности двух систем отсчета: Σ₁ — движущаяся с неизменным ускорением γ в направление оси X и Σ₂ — покоящейся, но находящейся в однородном гравитационном поле.

«Как известно, — констатировал Эйнштейн, — физические законы относительно Σ₁ не отличаются от законов, отнесенных к Σ₂; это связано с тем, что в гравитационном поле все тела ускоряются одинаково. Поэтому при современном состоянии наших знаний нет никаких оснований полагать, что системы отсчета Σ₁ и Σ₂ в каком-либо отношении отличаются друг от друга, и в дальнейшем мы будем предполагать полную физическую равноценность гравитационного поля и соответствующего ускорения системы отсчета.

Это предположение распространяет принцип относительности на случай равномерно ускоренного прямолинейного движения системы отсчета. Эвристическая ценность этого предположения состоит в том, что оно позволяет заменить однородное поле тяжести равномерно ускоренной системой отсчета, которая до известной степени поддается теоретическому рассмотрению» [1, т.1, с. 106].

Итак, в ноябре 1907 года Эйнштейн сделал первые попытки соединить СТО с ньютоновской теорией тяготения. Пока что речь идет об эквивалентности двух систем отсчета Σ₁ и Σ₂, но не об эквивалентности инерционной и гравитационной массы. К общей теории относительности Эйнштейн пришел через идею: «В свободном падении человек не ощущает своего веса!» Все предметы в поле тяготения падают с одним и тем же ускорением. Значит, свободно падающий наблюдатель не будет чувствовать, находится ли он в покое или участвует вместе с другими окружающими его предметами в ускоренном движении. Таким образом, с помощью учения Маха и Авенариуса об ощущениях он пришел к обобщенному принципу относительности, распространяющимся на равноускоренные системы отсчета. В 1907 году ни о каком тензоре кривизны пространства-времени речи не шло.

О нем ничего не говорилось и в работе 1911 года «О влиянии тяжести на распространение света», где Эйнштейн слегка развил идеи, высказанные в 1907 году. Поскольку эмпириокритицизм Маха и Авенариуса опирается на чувственный опыт, Эйнштейн в работе 1911 года решил подчеркнуть этот эмпирический момент (системы Σ₁ и Σ₂ он обозначил как K' и K, соответственно):

«Для ускоренной системы отсчета K' это следует прямо из принципа Галилея; для покоящейся же в однородном гравитационном поле системы отсчета K это следует из того опытного факта, что все тела в таком поле ускоряются равномерно и одинаково сильно. Этот опытный факт одинакового ускорения падения всех падающих в гравитационном поле тел является одним из наиболее общих фактов, установленных нами из наблюдений; несмотря на это, данный закон не нашел еще отражения в основах нашей физической картины мира.

Однако мы придем к весьма удовлетворительной интерпретации этого опытного закона, если допустим, что системы отсчета K' и K физически в точности равноценны, т. е. если допустим, что систему K равным образом можно рассматривать как систему, находящуюся в пространстве, свободном от поля тяжести, но при этом мы должны рассматривать K как равномерно ускоренную систему. При таком подходе нельзя говорить об абсолютном ускорении координатной системы, так же как нельзя в обычной [термина «специальная» или «частная» тогда еще не существовало] теории относительности говорить об абсолютной скорости системы. С этой точки зрения одинаковое ускорение всех падающих тел в гравитационном поле очевидно».[1, т.1, с. 166].

Позже Эйнштейн сообразил или ему подсказали, что «нельзя любое поле тяжести заменить состоянием движения системы без гравитационного поля, точно так же, как нельзя преобразовать все точки произвольно движущейся среды к покою посредством релятивистского преобразования». Это примечание к процитированному отрывку он сделал после перехода к дифференциальной геометрии и «опытному факту» равенства инерционной и гравитационной массы. Но тогда, в 1911 году, он еще не понимал, что не существует никакого «опытного факта» равенства ускоренной системы отсчета K' и покоящейся в однородном гравитационном поле системы отсчета K, так как в природе не существует самих систем K' и K.

В п. 18 работы 1907 года под названием «Пространство и время в равномерно ускоренной системе отсчета» Эйнштейн подготовил почву для вывода, который прозвучал в п. 19 под названием «Влияние гравитационного поля на часы». В п. 18 он получил выражение (30) [1, т.1, с. 108]:

σ = τ (1 + γ ξ/c²),

где γ — ускорение, ξ — текущее пространственная координата в системе Σ, τ — текущее время в системе Σ , при этом считается, что «свет в вакууме распространяется относительно Σ в течение элемента времени τ с универсальной скоростью c» [1, т.1, с. 107] и σ — «местное время» равноускоренной системы Σ, аналогичное «местному времени» Лоренца для равномерно движущихся систем. Затем формулу (30), автор переписал в виде формулы (30а) [1, т.1, с. 109]:

σ = τ(1 + Ф/c²),

где Ф = γ ξ «означает потенциал силы тяжести».

Теперь процитируем п. 19 полностью: «Если в точке P с гравитационным потенциалом Ф находятся часы, показывающие местное время, то, согласно соотношению (30а), их показания в (1 + Ф/c²) раз больше, чем τ, т.е. они идут в (1 + Ф/c²) раз быстрее одинаковых с ними часов, находящихся в начале координат. Пусть показания обоих этих часов воспринимаются каким-нибудь способом, например оптическим путем, наблюдателем, находящимся где-то в пространстве. Поскольку время Δτ, проходящее между показанием часов и моментом, когда это показание будет воспринято наблюдателем, находящимся где-то в пространстве, не зависит от τ, то часы в точке P идут в (1 + Ф/c²) раз быстрее, чем часы в начале координат. В этом смысле можно сказать, что процесс, происходящий в часах, — и вообще любой физический процесс — протекает тем быстрее, чем больше гравитационный потенциал в области, где разыгрывается этот процесс.

Существуют "часы", находящиеся в местах с различными гравитационными потенциалами, скорость "хода" которых можно проконтролировать с большой точностью; это — источники света с линейчатым спектром. Из сказанного выше следует [в предположении, что соотношение (30а) выполняется также в неоднородном гравитационном поле], что свет, приходящий от такого источника, расположенного на поверхности Солнца, обладает длиной волны, приблизительно на две миллионных доли большей, чем свет, испускаемый теми же атомами на Земле» [1, т.1, с. 110].

Данное место в п. 3 работы 1911 года «Время и скорость света в поле тяжести» Эйнштейн изложил более прозрачно: «Пусть ν₀ — частота некоторого элементарного источника света, измеренная с помощью часов U, находящихся в том же месте, где и источник. Эта частота не зависит от того, где установлен источник света вместе с часами. Представим себе, что источник и часы помещены, например, на поверхности Солнца (там находится наша система S₂). Часть испускаемого там света доходит до Земли (S₁), где мы часами U точно такой же конструкции, что и упомянутые выше, измеряем частоту ν приходящего света. Тогда

где Ф — (отрицательная) разность гравитационных потенциалов между поверхностью Солнца и поверхностью Земли.

Таким образом, согласно нашим представлениям, спектральные линии солнечного света должны несколько сместиться по сравнению с соответствующими спектральными линиями земных источников света в сторону красного конца спектра, а именно, на относительную величину

Это смещение можно было бы измерить, если бы были точно известны условия, при которых испускается солнечный свет. Однако ввиду того, что другого рода причины (давление, температура) также влияют на положение центра тяжести спектральных линий, трудно установить, действительно ли существует выведенное выше соотношение, в котором учитывается влияние гравитационного потенциала. ...

Итак, нельзя сказать, что оба часовых механизма, в S₂ и S₁ показывают правильное "время". Если мы определяем время в S₁ часами U, то мы должны измерять время в S₂ часами, которые идут в (1 + Ф/c²) раза медленнее, чем часы U, если их сравнить с часами U в одном и том же месте» [1, т.1, с. 170 – 171].

В связи с этим предсказанием красного смещения Эйнштейн сделал следующее примечание: «Джевил [L. F. Jewе11. J. phys., 1897, 6, 84] и особенно Фабри и Буассон [Ch. Fabrу, Н. Воissоn. Compt. Rend., 1909, 148, 688—690] действительно нашли подобное смещение узких спектральных линий в сторону красного конца спектра, вычисленного выше порядка, но приписали это смещение влиянию давления в поглощающем слое». Это значит, что он заранее знал о факте «покраснения» спектра, аналогично тому, как он заранее знал факты отклонения лучей вблизи Солнца и аномального смещения перигелия Меркурия. Поэтому было бы не правильно говорить, что Эйнштейн предсказал или спрогнозировал результаты многочисленных экспериментов, проводившихся после создания ОТО. Правильнее сказать: он подводил (чтобы не сказать подгонял) под имеющиеся в его распоряжении три факта свои теоретические изыски.

Но даже не это сейчас главное. От побочных явлений, наподобие эффекта Доплера, астрофизики научились отстраиваться, но позже обнаружилась другая беда. Е. Финлей-Фреундлих (E. Finlay-Frendlich) в 1954 году установил, что «смещения, найденные при наблюдении спектральных линий Солнца, сильно зависят от расстояния между центром солнечного диска и наблюдаемой точкой; смещение растет, асимптотически приближаясь примерно к предсказанному значению на краю диска. Физические условия, отвечающие за такую зависимость, должны быть однозначно установлены, прежде чем можно будет сказать подтверждают ли наблюдения существование предсказанного гравитационного смещения или нет» [2, с. 673].

Вот такая зависимость говорит в пользу оптического характера эффекта смещения спектральных линий. Вспомним, аналогичная зависимость имеет место для рефракции света в земной атмосфере: в зените она минимальная, на линии горизонта она максимальна. Очевидно, в атмосфере Солнца явления рефракции протекают по такому же сценарию. Похоже на то, что линии спектра сдвигаются тем больше, чем больше рефракция. В любом случае, указанная Финлей-Фреундлихом закономерность работает против гравитационного характера эффекта смещения спектральных линий.

Авторы статьи [3] заостряют внимание читателя на двух различных объяснениях покраснения фотона. В аннотации к статье они указывают, «что при удалении фотона от гравитирующего тела (например, Земли), его измеряемая частота уменьшается. Это явление объясняется в литературе двумя различными способами. Первое объяснение сводится к тому, что измеряющие частоту часы (атомы или атомные ядра) сами идут быстрее (увеличивают свои характерные частоты) на большей высоте, а частота фотона в статическом гравитационном поле с высотой не меняется. Так что фотон краснеет только относительно часов. Второе объяснение заключается в том, что фотон краснеет потому, что теряет свою энергию, преодолевая притяжение гравитационного поля. Это второе объяснение, особенно широко распространенное в научно-популярной литературе, оперирует такими понятиями как «гравитационная масса фотона» и «потенциальная энергия фотона». К сожалению, такая интерпретация зачастую встречается и в ряде научных статей и серьезных монографий по общей теории относительности, где она используется в качестве «наглядного» пояснения формул, полученных математически безупречным образом. Мы показываем, что такая интерпретация неправильна и создает путаницу в простом вопросе» [3, с. 1141].

Можно, конечно, говорить, что рассуждения о «гравитационной массе фотона» и «потенциальной энергии фотона» ошибочны, только ведь существует еще один релятивистский эффект, отклонение луча света вблизи гравитирующего тела, которое без этих понятий объяснить невозможно. Но об этом поговорим позже; сейчас напомним, что помимо гравитационного красного смещения, отклонения луча света вблизи Солнца и аномального сдвига перигелия Меркурия, Эйнштейн в работе 1911 года «предсказал» четвертый опытный факт, который можно было бы сравнительно просто проверить, но который, однако, никогда не проверялся. Речь идет о зависимости скорости света от гравитационного потенциала:

«Если мы обозначим через c₀ скорость света в начале координат, то скорость света c в некотором месте с гравитационным потенциалом Ф будет равна

        (3)

По этой теории, принцип постоянства скорости света справедлив не в той формулировке, в какой он кладется в основу обычной [специальной] теории относительности» [1, т.1, с. 172].

Выступление на радио

В статье 1907 года «О принципе относительности и его следствиях» Эйнштейн также выводил формулу изменения скорости света в ускоренной системе отсчета, в которой вместо константы c нужно было использовать зависимую от гравитационного потенциала (Ф = γx, где γ — постоянное ускорение) переменную скорость c(1 + Ф / c²).

«Отсюда следует, — продолжал он, — что световые лучи… искривляются гравитационным полем; изменение направления, как легко видеть, составляет γsinφ / c² на 1 см пути света, где φ означает угол между направлениями силы тяжести и светового луча. … К сожалению, — добавил он, — согласно нашей теории, влияние поля тяготения Земли так незначительно (вследствие того, что величина γx / c² мала), что нет никаких перспектив на сравнение результатов теории с опытом» [1, т. 1, с. 113].

Таким образом, здесь искривление луча, идущего от звезды, было связано с изменением скорости света, как это происходит, например, в воде, для которой преломление световых лучей тоже зависит от изменения скорости света в водной среде. Потом Эйнштейн откажется от своего положения, согласно которому скорость света меняется в ускоренной системе отсчета, и придет к постулату о неизменности скорости света в любых системах отсчета. Искривление луча будет происходить в результате искривления пространства-времени. Однако это положение ОТО еще не было взято на вооружение в статье 1911 года «О влиянии силы тяжести на распространение света». В преамбуле к ней он писал:

«В работе, опубликованной четыре года назад, мы уже пытались ответить на вопрос, влияет ли тяготение на распространение света. Мы снова возвращаемся к этой теме, так как нас не удовлетворяет прежнее изложение вопроса; кроме того, мы теперь еще раз убедились в том, что одиц из наиболее важных выводов указанной работы поддается экспериментальной проверке. Оказывается, что лучи, проходящие вблизи Солнца, согласно излагаемой ниже теории, испытывают под влиянием поля тяготения Солнца отклонение, вследствие чего должно произойти кажущееся увеличение углового расстояния между оказавшейся вблизи Солнца неподвижной звездой и самим Солнцем почти на одну дуговую секунду.

Развитие этих идей привело также к некоторым результатам, относящимся к тяготению. Так как изложение всех рассуждений было бы громоздким в ущерб ясности, то ниже будут даны только некоторые совершенно элементарные соображения, с помощью которых удобно ориентироваться в предпосылках и в логическом развитии теории. Выведенные в настоящей работе соотношения, даже если теоретическое основание их и соответствует действительности, являются верными только в первом приближении» [1, т. 1, с. 165].

В п. 4 «Искривление лучей света в гравитационном поле», исходя из формулы (3) и применяя принцип Гюйгенса, Эйнштейн получает выражение (4) для отклонения луча на угол α от нормали:

.         (4)

Вслед за формулой (4) он сразу записал выражение (5):

,         (5)

которое, однако, не связано прямой математической цепочкой с выражением (4). Подставляя значения гравитационной постоянной (k) и массы Солнца (M), мы получаем простую зависимость угла отклонения α от расстояния Δ, на котором луч света, идущий от звезды, проходит мимо центра затемненного солнечного диска. При касательном луче, т.е. когда Δ = R — радиус Солнца, отклонение будет максимальным, равным 0,87".

Заметим, что интеграл от cos θ, взятый в пределах интегрирования θ = ± π/2, равен 2, но как от гравитационного потенциала, фигурирующего под интегралом (4), перейти к закону всемирного тяготения, фигурирующему в (5), — не совсем понятно. Таким образом, в словах, сказанных в преамбуле о «громоздкости» рассуждений, которая якобы нанесет «ущерб ясности» изложения в действительности заключалась некая хитрость. Ее в 1921 году раскрыл Филипп Ленард [5]. Он опубликовал еще раз малоизвестную работу Зольднера [4], в которой самым прозрачным образом получался числовой результат, соответствующий формуле (5). Это позволило Ленарду обвинить Эйнштейна в плагиате.

По статье 1911 года мы видим, как автор длинно рассуждал об изменении энергии и массы в системе с различным гравитационным потенциалом. Он писал выражения 1a и 1b для энергии и массы:

      ,

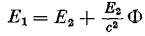
(правда, о весомости света он так ничего и не сказал). Однако эти его метания никак не объясняют главную формулу статьи 1911 года: откуда взялась формула (5), так и осталось загадкой.

Между прочим, хождение вокруг да около — так характерно для Эйнштейна. Например, в статье «К электродинамике движущихся тел» он тоже долго ходил вокруг да около измерения отрезков пути и периодов времени с помощью светового луча, только заветные релятивистские формулы у него так и не появились (см. Как создавалась специальная теория относительности). Тем не менее, видимость того, что преобразования Лоренца получаются именно из этой процедуры измерения, у невнимательного читателя осталась.

Зольднер вместе с Ньютоном и Лапласом считал, что свет состоит из весомых частиц. Отсюда становится понятно, почему световые лучи от звезд притягиваются Солнцем. В статье [9] релятивист Захаров «предположил, что фотон обладает энергией E = hν и массой m = E/c²», против чего как раз категорически возражали авторы статьи [3]. Эти формулы Захаров, как и Эйнштейн формулы 1a и 1b, не использует при выводе угла отклонения, их можно было бы не писать, но от замалчивания принципиальных проблем они не исчезают.

Всякий честный физик должен хорошо помнить: электромагнитное излучение или фотоны — если допустить, что свет имеет корпускулярную природу, — не имеют массы. Тогда не понятно, по какой причине световой луч должен отклоняться в гравитационном поле. Пусть, в соответствии с ОТО, луч света отклоняется вместе с искривлением пространства-времени. Но, как доказал еще Пуанкаре (см. От Пуанкаре назад к Канту), внешний наблюдатель этого не обнаружит. Очевидно, что отклонение лучей, наблюдаемое при солнечном затмении, происходит за счет какой-то другой причины (о ней мы подробно поговорим позже).

– II –

Искомый угол отклонения определил Иоганн Георг фон Зольднер (15.06.1776 – 18.05.1833), немецкий астроном, директор обсерватории Мюнхенской Академии, прекрасный математик, прославившийся своей работой в области геодезии. В 1801 году он послал в «Berliner Astronomisches Jahrbuch» («Берлинский астрономический ежегодник») статью «Об отклонении светового луча от его прямолинейного движения притягивающим всемирным телом, мимо которого он близко проходит», изданную в 1804 году [4]. В ней задолго до Эйнштейна на основе корпускулярной теории весомого света и всемирного закона тяготения он получил выражение, соответствующее формуле (5).

Иоганн Георг фон Зольднер
(15.06.1776 – 18.05.1833)

Зольднер руководствовался принятой в его время картиной мира Лапласа, который сказал сакраментальную для всякого релятивиста фразу: сила притяжения небесного тела может быть столь огромна, что частицы света не смогут его покинуть. Релятивисты думают, что Лаплас своим прозорливым умом догадывался о существовании черных дыр, что, конечно, не так, поскольку у французского астронома не было идей о существовании параллельных вселенных, куда можно попасть через черные дыры. В статье [4] немецкий астроном отметил достижения в практической астрономии, которые рано или поздно потребуют более точной теории. Он напомнил о «значительных отклонениях» в случае аберрации света, «однако могут найтись отклонения, которые так малы, что трудно будет решить, являются ли они истинными отклонениями или ошибками измерения» [4, с. 161]. Отклонения светового луча вблизи «притягивающего всемирного тела» является функцией высоты; было бы желательно установить максимум такого отклонения, который будет наблюдаться при касании луча поверхности «гравитирующего тела», как говорят сейчас.

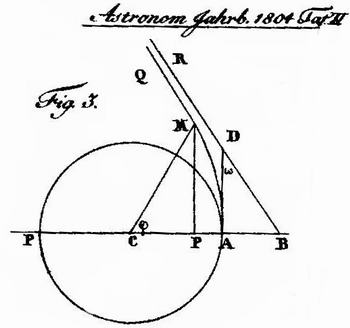
Зольднер вычертил Fig. 3, где отметил точку C, в которой находится «притягивающее всемирное тело». Ускорение силы тяжести в точке A, расположенной на поверхности тела, равно g. Световой луч, коснувшись поверхности тела в точке A, пойдет не по прямой AD, а по гиперболической кривой AMQ. Введем обозначения: CM = r, CP = x, MP = y; углы MCP = φ и ADB = ω. Долее Зольднер написал: «Сила (Die Kraft), с которой световой луч притягивается телом в точке M по направлению MC, равна 2gr ^–2».

Величина, которая здесь упоминается не является силой, поскольку не имеет соответствующей размерности. Судя по равенствам (I) и (II), ее можно было бы вместе с Захаровым [9] назвать изменением вектора скорости в результате действия силы притяжения тела. Коэффициент 2 здесь тоже введен для удобства формального вывода (смысл этих искусственных построений выяснится позже). Далее он разложил «силу» на вертикальную и горизонтальную проекции:

    и    

и приравнял их к соответствующим вторым производным:

    (I)
    (II)

Умножая первое из этих уравнений на –sin φ, второе на cos φ и складывая их, получаем:

    (III)

Умножая первое на cos φ, второе на sin φ и складывая их, получаем:

    (IV)

Чтобы уменьшить число переменных в этих уравнениях, выразим x и y через r и φ

    и     .

Если их продифференцировать, получим:

    и     .

Если продифференцировать еще раз, получим:

    и     .

Подставим эти значения ddx и ddy в (III), получим:

.

Итак, имеем:

    (V)

Из (IV):

    (VI)

Умножим (V) на rdx, будем иметь:

.

Проинтегрируем числитель последнего равенства, получим:

,

где C — произвольная постоянная. Чтобы определять ее, заметим, что величина r²dφ равна двойной площади, которую заметет радиус-вектор r за время dt. Но эта площадь, описанная в течение первой секунды времени, равна AC · v. Если принять AC за единицу, что мы будем всегда подразумевать, то окажется, что C = v. Таким образом, имеем:

или

    (VII)

Подставим (VII) в (VI):

.

Умножим последнее уравнение на 2dr:

.

Еще раз проинтегрируем:

,

где D постоянная, зависящая от постоянных, входящих в уравнение. Отсюда можно найти время:

.

Подставим это значение dt в уравнение (VII):

.

Чтобы проинтегрировать это уравнение, приведем его к виду:

.

Обозначим:

,

тогда будем иметь:

.

Подставим выражения для dz и z в уравнение для dφ, получим:

Отсюда возьмем интеграл:

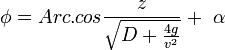
где α — постоянная величина. После преобразований, получим:

Для α = 0, получаем:

Для φ = 0 и r = AC = 1, получаем:

Таким образом, мы избавились от постоянной D:

Произведем следующие преобразования:

    (VIII)

Сейчас нам необходимо понять, каков характер кривой (VIII), зависящей от переменных r и φ. С этой целью снова вернемся к переменным x и y, но уже в виде (Fig. 3):

Подставим эти значения в уравнение (VIII), получим:

.

Последнее уравнение преобразуем к виду:

.     (IX)

Сравнение (IX) с общим уравнением для всех видов конических сечений:

.

подсказывает нам, что уравнение (IX) описывает гипербулу, «так как для всех известных нам всемирных тел 4g меньше, чем v², таким образом, коэффициент при x² должен быть положительным». Не искривленный луч прошел бы в направлении асимптоты BR (Fig.3), но в глаз наблюдателя он попадает по направлению AD; угол пертурбации ω определяется соотношением:

.

Из общих свойств гиперболы мы знаем:

.

Подставим это значение в общее уравнение гиперболы:

,

тогда получаем:

.

Если сравнить теперь коэффициенты при x и x² с теми, что стоят в уравнении (IX), то получим горизонтальный катет:

и вертикальный катет равен:

Отсюда находим значение тангенса tang ω:

В этом выводе Зольднер принимал радиус Солнца за единицу (R = 1). Для того чтобы рассчитать угол ω = tang ω, нам нужно брать вместо ускорения g произведение gR, только в этом случае произойдет согласование единиц измерения с квадратом скорости (v²). Значение радикала из-за малости вычитаемого можно принять за v = c, т.е. равным скорости света. Тогда окончательная формула будет выглядеть так:

ω = 2gR / c².     ( * )

Ускорение свободного падения на поверхности Солнца равно g = 274 м/с², скорость света — c = 3 · 10⁸ м/с, радиус Солнца — R = 6,96 · 10⁸ м. Подстановка этих величин в выражение ( * ) дает угол ω = 4,238 · 10 ^–6 радиан. В одной угловой секунде содержится 4,848 · 10 ^–6 радиан, следовательно, искомое отклонение равно ω = 0",875. Зольднер определил по известным на то время параметрам, что отклонение светового луча от асимптоты BR (Fig.3) равно ω = 0",84 (он называл его углом пертурбации).

– III –

Филипп Ленард

После обнародования Ленардом факта плагиата Эйнштейном найденного Зольднером величины угла пертурбации (ω) данный исторический казус тщательно изучался некоторыми исследователями на Западе, в частности, Jaki [6], Treder [7], Will [8], и в нашей стране Захаровым [9]. Выяснилось, что впервые значение ω было вычислено еще в 1784 году английским физиком Генри Кавендишем. Найденный им результат не опубликован, но его можно найти в адресованном Джону Митчеллу письме. В работе Эйнштейна 1911 года формула (5) содержит интеграл, который не фигурирует в работе Зольднера 1801 года. По-видимому, Милева Марич — больше некому — слегка модернизировала его вывод, который затем был восстановлен исследователями [6] – [8]; ниже приводится этот «эйнштейновский» вывод, взятый из работы [9, с. 78].

Зольднер, как мы знаем, исходил из величины 2gr ^–2. Поскольку ускорение равно g = GMr ^–2, то его результат для ω в форме уравнения (*) можно пердставить в следующем виде:

    (1)

Здесь Θ = α = sinα = tgα = tangω = ω — максимальный угол отклонения или угол пертурбации луча света, проходящего на расстоянии солнечного радиуса R; M — масса Солнца; G — гравитационная постоянная; c — скорость света. Релятивистский результат отличается ровно в два раза:

    (2)

Для дальнейшего изложения воспроизведем рис. 2 из работы [9].

Найдем изменение проекции скорости на вертикальную ось, как это делал Зольднер:

    (3)

где

Интервал временени связан со значением интервала по горизонтальной оси следующим образом:

    (4)

предполагая, что Если ввести замену переменной: , то

    (5)

Поскольку то Тогда

    (6)

Полное изменение скорости в вертикальном направлении можно вычислить посредством определенного интеграла:

    (7)

Значение интеграла равно 2:

    (8)

Следовательно, имеем:

    (9)

Отсюда находим искомый угол отклонения:

    (10)

Здесь по формуле (7) мы можем судить о выводе формулы (5), приведенной в эйнштейновской работе 1911 года. Отсутствие связи ее с формулой (4), указывает нам на то, что обвинения Ленарда не были безосновательными. Однако недобросовестные историки релятивизма в этом месте переключаются на тему, не связанную с наукой. Они напоминают о националистических пристрастиях и политических предпочтениях Ленарда. Разумеется, это не может оправдать научную недобросовестность Эйнштейна.

Захаров пытался следовать Зольднеру, но не воспроизвел его вывод точно. На это указывает, в частности, то, что формула (3) копирует приближенное выражение (*), а не точную формулу для tang ω. Очевидно, Захаров хотел восстановить логику рассуждений эйнштейновской статьи 1911 года, но не самого Зольднера, логика которого не была безупречной. На это указывает некоторая натяжка в отношении силовой характеристики в виде малопонятной величины 2gr ^–2, с которой начался его вывод. Отсюда и захаровский метод лишен той лаконичности и прозрачности, которую можно найти, например, в брошюре А.М. Петрова «Антиэйнштейн».

Петров привел элементарный вывод, который, по-видимому, еще не был известен астрономам начала XIX века, когда писал статью Зольднер, но, наверняка, был хорошо известен астрономам начала XX века, когда писал статью Эйнштейн (хотя Захаров предположил, что об этом угле отклонения знал уже Ньютон). Именно потому, что Эйнштейн, не знавший основ небесной механики, воспроизвел допотопную логику Зольднера, прикрываясь фразой о якобы громоздкости вывода (на самом деле вывод несложный), мы можем с уверенностью констатировать: плагиат имел место быть.

Итак, процитируем из брошюры Петрова следующий фрагмент: «... В теперешнем, "усечённом", виде школьная программа содержит минимум знаний, позволяющий "не плавать" в задачах по элементарной геометрии и небесной механике. Приведём решение задачи об отклонении луча света гравитационной силой, ориентируясь на уровень знаний нынешней обычной (без "математического уклона") средней школы.

Малый объект, пролетающий мимо массивного небесного тела, движется, в зависимости от величины его относительной линейной скорости, по параболе или гиперболе. Для световых скоростей, естественно, имеет место второй вариант.

Заглянем в справочник [Выгодский М.Я. Справочник по высшей математике, — М.: Физматлит, 1995, c. 115, рис. 109] и найдём формулу для расстояния между фокусом (центром притяжения) и произвольной точкой конического сечения (эллипса, параболы, гиперболы) в зависимости от величины угла, под которым видна эта точка из фокуса (величина угла отсчитывается от, действительной для гиперболы, оси геометрической фигуры):

ρ = p / ( 1 + ε cos φ ).

где p — параметр, ε — эксцентриситет конического сечения.

В интересующем нас случае эксцентриситет ε >> 1, поэтому расстояние от фокуса до вершины гиперболы выражается формулой:

p / ε = R,

где R = 6,96 · 10⁸ м — радиус Солнца.

Поскольку радиус кривизны в вершине гиперболы (как и других фигур конического сечения) равен параметру p, то в этой точке имеет место следующий баланс сил, приведённых к единице массы:

с² / p = g,

где c = 3 · 10⁸ м/с — скорость света, g = 274 м/с² — ускорение свободного падения на поверхности Солнца.

Отсюда находим величину параметра p

p = с² / g = 3,285 · 10¹⁴ м.

Теперь определяем величину эксцентриситета гиперболы:

ε = p / R = 4,72 · 10⁵,

что позволяет найти величину бокового смещения луча света:

δ = R – ρ cos φ = ρ / ε.

При ρ >> R боковое смещение луча света равносильно повороту луча в пространстве на постоянный угол, численно равный:

α = δ / p = 1 / ε = 2,119 · 10 ^–6 радиан.

В угловых секундах эта величина составит 0",437. С учётом второй полуветви гиперболы (от звезды до Солнца) полученный результат следует удвоить: 0",874 » [18, с. 12 – 13].

– IV –

Итак, в 1911 году Эйнштейн указал отклонение луча света α = 0",83, рассчитанное по методике Зольднера (сегодняшние постоянные дают величину 0",874). Это отклонение релятивисты называют ньютоновским, так как пространство вблизи Солнца и других массивных тел предполагается евклидовым, плоским или неискривленным. Расчетное отклонение света «по Эйнштейну» оказалось в два раза большим, т.е. 1",74 (некоторые детали вывода этой величины приводятся на с. 442 и с. 503 первого тома СНТ [1]). Но уже в 1914 году, «до того как был получен правильный ответ, Эйнштейн написал Бессо со свойственной ему уверенностью: "Я более не сомневаюсь в справедливости своей теории, независимо от того, увенчается ли успехом наблюдения солнечного затмения". Зигзаги истории несколько раз позволяли ему избежать неприятной ситуации, когда полученный им неверный результат вступил бы в противоречие с опытными данными» [10, с. 290].

Дальше началась эпопея с опытным подтверждением отклонения α = 1,74". Прошло без малого столетье, как Эддингтон привез из экспедиции 1919 года первые астрономические данные, якобы подтверждающие ОТО, но споры между релятивистами и антирелятивистами вокруг величины 1,74" и как ее можно объяснять так и не угасли. Действительно, представленный Эддингтоном отчет, выдержки из которого приводятся ниже, имеет слишком много изъянов. В частности, фигурирующая в нём диаграмма 2 является ничем иным как откровенной подгонкой под нужный для релятивистов результат. В своих антирелятивистских работах А.К. Тимирязев приводит совершенно иные диаграммы, дающие намного более объективную картину, которую получили, в частности, астрономы по результатам затмения 1921 года над Австралией. Эти эмпирические данные релятивисты, разумеется, не приводят, так как они ставят жирный крест на одном из трех подтверждений ОТО.

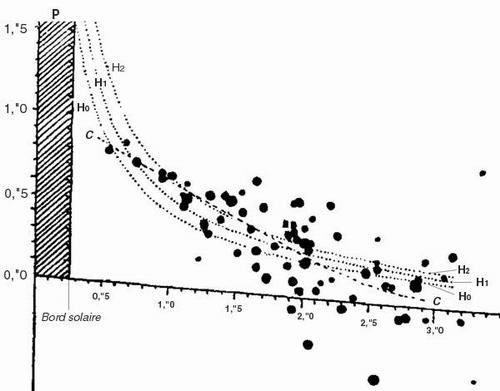
Рис. 1. Отклонение лучей от звезд вблизи солнечного диска по наблюдениям затмения 1921 года над Западной Австралией (Wallal). Чертеж взят из статьи А.К. Тимирязева «Теория относительности Эйнштейна и диалектический материализм» (Под Знаменем Марксизма» 1924 г., № 8–9, с. 142 – 157; № 10–11, с. 93 — 14, рис. 1).

Чтобы тщательно разобраться в данном вопросе, призываем читателя внимательно изучить две статьи А.К. Тимирязев под заголовками: Теория относительности Эйнштейна и махизм и Теория относительности Эйнштейна и диалектический материализм [11]. Приведем из последней статьи рис. 1 и дадим к нему разъяснения Тимирязева. Он пишет: «По горизонтальной прямой [она несколько наклонена на чертеже, благодаря внесению поправок] отложены выраженные в градусах расстояния звезд от центра солнца, заштрихованная полоса изображает область P, занятую солнцем. От центра до края, на вертикальной оси отложены смещения положения звезд, выраженные в секундах дуги, пунктирная кривая H₀ соответствует теории Эйнштейна [1,"7/r]. Черные точки представляют результаты измерений с той или другой звездой, причем, чем больше размер кружка, тем больший вес имеет данное наблюдение. Кривые H₁ и H₂ имеют больший постоянный коэффициент, чем в эйнштейновской формуле [2,"05/r и 2,"10/r, соответственно]. Если вычислить по формуле, предполагающей простой закон Ньютона (вычисление Сольднера 1811 г.; тот же результат получится по теории Дж. Дж. Томсона, приписывающей гравитационную массу эфиру, увлекаемому силовыми линиями в световой волне), то кривая пройдет немного ниже, но также через области, густо покрытые точками».

А.К. Тимирязев

Далее Тимирязев приводит слова Э. Эскланьона, директора Страсбургской обсерватории, сказанные по поводу рис. 1: «Другими словами, для геометрического изображения данного ограниченного количества точек наблюдений не существует одной кривой, но целый пучок кривых, которые могут удовлетворить этому условию, и в этом смысле все они в одинаковой мере законны и приемлемы. Изображение должно выражаться не с помощью линии, а с помощью настоящей "дороги", проведенной через группу точек; дорога эта тем шире, чем больше средние отклонение точек. Что же касается совокупности отклонений вблизи солнца, то здесь точно так же дорога остается еще настолько широкой, что в тех пределах расстояния от солнца, где измерения фактически были сделаны, изображение с помощью формулы Ньютона 0,"9/r почти настолько же законно, что и с помощью Эйнштейновой формулы 1,"7/r и что лучшая из формул такого рода будет скорее 2,"0/r .

Итак, здесь-то и заключается весь вопрос: фактически, на этой "дороге" остается много места для одновременного переезда весьма разнообразных экипажей, для теорий — по природе своей весьма различных; таким образом, в настоящее время нельзя сказать, для какого экипажа подходит больше всего приведенная дорога» [L'Astronomie. Bulletin de la Societe astronomique de France. 38 Annee, Mai 1924, p. 184].

Нашим читателям разыскать в Интернете книгу А.К. Тимирязева «Введение в теоретическую физику» и тоже почитайте ее. Она, конечно, сильно устарела, но всё же дает некоторый ориентир, каким образом нужно подходить к проблемам, возникшим в теори относительности и квантовой механике. Пусть не пугают вас устаревшие слова из марксистского лексикона, постарайтесь как следует усвоить аргументацию автора. Относительно затронутой здесь темы А.К. Тимирязев, в частности, писал:

В 1919 и затем в 1922 гг. были произведены снимки во время солнечного затмения, на которых были сделаны измерения положения звезд; во всех газетах и журналах появились статьи, в которых наперебой объявляли об удивительном оправдании пророчества эйнштейновой теории. Однако и в этом случае критический анализ фактов указывает, что о доказательстве теории Эйнштейна здесь не может быть и речи… Проф. В. Г. Фесенков приходит к выводу: «Отсюда видно, что наблюдаемое смещение звезд около Солнца во время затмения представляет собой чрезвычайно сложное явление и ни в коем случае не может рассматриваться как подтверждение теории относительности». Любопытно отметить, что во время затмений, происходивших после 1923 г., никто не производил этой проверки теории Эйнштейна, хотя было бы в высшей мере важно решить вопрос, подтверждаются ли предсказанные результаты или нет…

Однако все это тщательно замалчивается; в особенности тенденциозно составлена книжка проф. С.И. Вавилова «Экспериментальные основания теории относительности». Все предсказания у проф. Вавилова признаны оправдавшимися, а возражения — несущественными, и, что всего хуже, в качестве литературы указаны как раз те обзоры и критические статьи, в которых авторы приходят к прямо противоположным результатам. Так, например, к гл. VI, в которой доказывается «тяготение света», указана литература, которая опровергает выводы Эйнштейна, как, например, Эскланьон, В. Г. Фесенков (цитированная нами статья) и Крооз, и ни одним словом не упоминается о том, что эти авторы приходят к диаметрально противоположным результатам, чем это говорится в тексте. То же самое имеет место и в других главах; поэтому, если читатель сам не ознакомится с приведенной в конце книги литературой, он получит совершенно превратное представление об экспериментальных исследованиях, связанных с теорией Эйнштейна.

Вообще вокруг теории относительности создалась совершенно особая атмосфера. Защищается она с необыкновенной страстностью, а противники ее подвергаются всяким нападкам, из чего ясно, что здесь речь идет вовсе не о деталях какой-либо теории, в этой области отражается классовая борьба, участники которой не отдают себе даже отчета в том, что они в ней участвуют. Вне всякого сомнения, за теорию ухватились все враги материализма, а против нее выступают, как правило, материалисты более или менее последовательные. Эта борьба облегчается тем, что теория Эйнштейна не связана ни с какими техническими вопросами, и поэтому всякие идеалистические извращения науки в этой области не отражаются на развитии техники» [Введение..., с. 388].

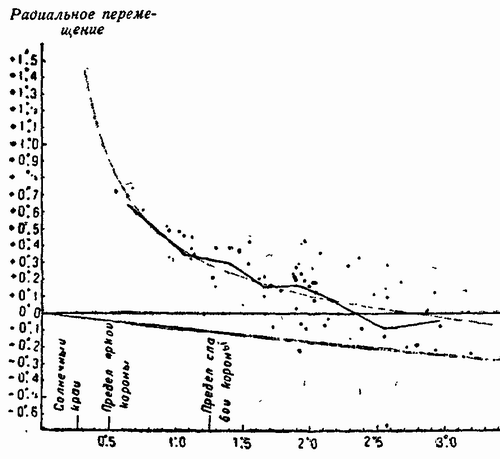
Рис. 2. Отклонение лучей от звезд вблизи солнечного диска. Чертеж взят из учебника А.К. Тимирязева «Введение в теоретическую физику» (М.,Л.: Гос. Тех.-Теор. Изд-во, 1933, с. 388, рис. 172).

Тогда, в 1920-х годах, из-за борьбы двух противоборствующих сторон нелегко было установить истину; еще сложнее это сделать сегодня. Релятивисты ни за какие деньги не опубликуют рис. 1 или рис. 2, они будут морочить голову рис. 3, где отклонения лучей от 15 звезд даны по результатам того же самого затмения 1921 года, но картинка приведена из отчета, выполненного авторами W. W. Campbell и R. J. Trumpler. В статье Ивченкова [12], откуда взят этот рисунок, сказано: "figure from Misner et al, Gravitation, Freeman and Co., 1973, 1104". Таким образом, рис. 3 вычерчен, видимо, не совсем беспристрастно. Если дело касается проверки ОТО, то здесь многое зависит от установки автора — является ли он релятивистом или нет.

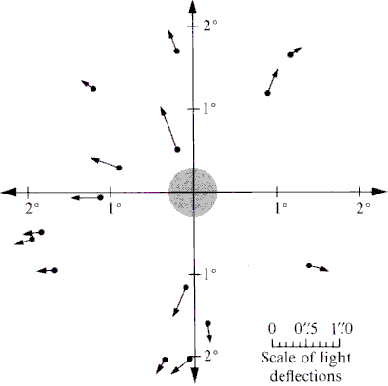
Рис. 3. Видимые отклонения звезд по затмению 1921 года,
описанному в отчете W. W. Campbell и R. J. Trumpler.
Взято из работы [12].

Игорь Талызин прислал мне картинку из книги [19], где в качестве подтверждения ОТО приведен рис. 4, аналогичный предыдущему рисунку, но соответствующий затмению 1922 года. На этом рисунке мы видим уже 37 звезд, для которых указаны координаты, а стрелками — направления и смещения всех звезд.

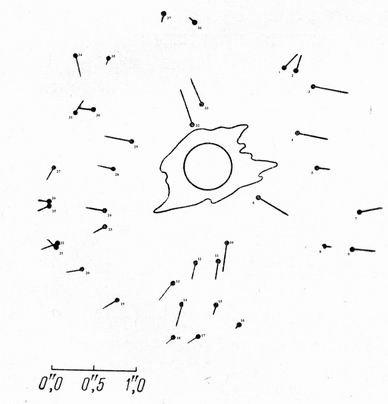
Рис. 4. Видимые отклонения звезд по затмению 1922 года.
Взято из работы [19].

В соответствии с рис. 4, Талызин произвел измерения координат и величину смещения всех 37 звезд [20, табл. 1], а затем вычислил углы отклонения лучей света вблизи Солнца по классической теории Ньютона и ОТО [20, табл. 2]:

           

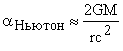
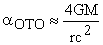
"На рисунке видно, — заостряет наше внимание Талызин, — что направление смещений звёзд не совпадает с направлением от центра диска Солнца. У луча света нет гравитационных причин отклоняться в направлении, перпендикулярном к направлению на центр Солнца. Поэтому естественно будет такие отклонения целиком относить к ошибкам измерения, а для расчетов принимать во внимание только проекцию смещения на направление от центра Солнца".

В этой связи выскажем еще одно предположение. Нерадиальный сдвиг звезд, зафиксированный при затмении 1922 года, может происходить не только из-за погрешности измерения, но и по причине случайных флуктуаций плотности околосолнечного плазменного вещества. Разумеется, оно присутствует, но никогда не учитывается релятивистами. В любом случае, указанные Талызиным "странные" отклонения, которые можно обнаружить и на рис. 3, соответствующему затмению 1921 года, носят явно не гравитационный характер. Таким образом, данные наблюдения солнечного затмения 1922 года еще больше, чем данные 1921 и уж, тем более, 1919 года, убеждают нас в беспомощности релятивистов подтвердить свое учение на основе отклонения лучей от звезд вблизи Солнца.

(К сказанному добавим, что на сайте Талызина имеется также сноска на графические данные наблюдения еще двух затмений – 1919 и 1952 гг. [21] ).

Следует особо подчеркнуть, что вопрос об отклонении лучей света стоял в тот период на повестки дня многих астрономических обсерваторий отнюдь не в связи с теоретическими разработками Эйнштейна. Как и аномальный сдвиг перигелия Меркурия, данная проблема возникла самостоятельно, но попала в сильнейший резонанс в связи с релятивистскими претензиями объяснять с помощью одной формалистской теории все явления природы. Подобно тому, как под громкий, но непонятый эксперимент Майкельсона — Морли Эйнштейн подгадал с СТО, точно так же под непонятый эффект аномального движения Меркурия и всеми ожидаемый эффект отклонения лучей вблизи Солнца он подгадал с ОТО. Релятивисты же представляют этот эпистемологический процесс в обратном порядке: от теории к эмпирии. У непосвященного создается впечатления, будто гений Эйнштейна привел в движение все обсерватории мира с целью проверки его теории.

По сообщению Пайса [10, с. 290] уже в 1912 году, когда ОТО находилась в самом зачаточном состоянии, а об Эйнштейне мало кто слышал, была откомандирована в Бразилию экспедиция аргентинских астрономов для наблюдения отклонение лучей света вблизи солнечного диска, покрытого Луной. Увы, из-за сильнейших ливней эти наблюдения были сорваны. Затем немецкая экспедиция под руковдством Эрвина Фрейндлиха, с которым впоследствии познакомился Эйнштейн, была послана в Крым с той же целью: для наблюдения затмения 21 августа 1914 года. К сожалению, началась Первая мировая война, так что немцам пришлось в спешке покинуть «вражескую» территорию. По причине военных действий было пропущено и затмение 1916 года в Венесуэле. Попытка американцев (руководитель Хейл) зафиксировать в 1918 году отклонение лучей от звезд вблизи затемненного Луной диска Солнца тоже не дали убедительных результатов. Все эти неудачи широко освещались в прессе, поскольку в ту эпоху интерес к науке был необычайно высок.

Почему астрономы заинтересовались отклонением лучей вблизи Солнце? Дело в том, что задолго до создания ОТО всем астрономам было хорошо известно явление атмосферной рефракции, т.е. преломления лучей света в атмосфере Земли, которое вызывало заметное смещение звезд на небосводе особенно вблизи горизонта. Звезду, реально зашедшую за горизонт на угол, равный 35'24", мы видим в точности на линии горизонта. При зенитном расстоянии в 45° это отклонение составит 58", т.е около одной угловой минуты в сторону зенита. И хотя явление рефракции было известно еще Птолемею, именно в начале XIX века стали составляться точные таблицы так называемой «средней рефракции», т.е. не учитывающей температурные поправки, охватывающие околозенитные области.

Заметим, что все без исключения вещества, в том числе и не прозрачные, преломляют электромагнитные волны. Но лучше всего этот эффект наблюдать на примере «преломленной» палки, опущенной в воду. Если Солнце обладает атмосферой, то она, непременно, должна вызвать преломление лучей от звезд. С помощью этого вполне материального явления астрономы надеялись что-то узнать о плотности солнечной атмосферы и ее электромагнитных свойствах. Однако ажиотаж, поднятый вокруг теории относительности, смешал все их карты. На первый план вышли бесконечные споры физиков о величине гравитационного или чисто геометрического искривления электромагнитных волн. Проблема плотности солнечной атмосферы была задвинута на второй план.

О причинах отклонения лучей от звезд вблизи солнечного диска мы поговорим в следующем разделе (Аномальное движение перигелия Меркурия), а пока расскажем, что и как измерил Эддингтон. Напомним, в феврале 1917 года королевский астроном Фрэнк Дайсон (1868 — 1942) указал на особо удачное расположение звезд в зоне затмения Солнца, которое должно произойти 29 мая 1919 года, по сравнению с предыдущими затмениями. Накануне затмения были организованы две экспедиции — в Собраль (Бразилия) и на крошечный португальский остров Принсипи у западного побережья Африки недалеко от Гвинеи. Первую экспедицию возглавил Эндрю Кроммелин из Гринвичской обсерватории, вторую — Артур Эддингтон, в то время директор обсерватории при Кембриджском университете.

– V –

Определение отклонения луча света в гравитационном поле Солнца по данным наблюдений, проведенных во время полного солнечного затмения 29 мая 1919 г. Dyson F. W., Eddington A. S., Davidson С, Phil. Trans. Roy. Soc, ser. A, 220, 291 (1920); русский перевод взят из сборника статей «Альберт Эйнштейн и теория гравитации» (М.: Мир, 1979, с. 564-570).

« I. Цель экспедиций.

1. Целью экспедиций являлось определить, какое воздействие оказывает (если оно оказывает) гравитационное поле на траекторию проходящего через него луча света. Если не считать возможных неожиданностей, у нас было, по-видимому, три альтернативы, между которыми особенно желательно было провести выбор:
1) гравитационное поле не оказывает влияния на траекторию луча света;
2) гравитационное поле действует на энергию, или массу, светового луча так же, как и на обычное вещество; если закон тяготения носит строго ньютоновский характер, то это приводит к кажущемуся смещению во внешнем направлении звезды у края солнечного диска, равному 0",87;
3) ход луча света согласуется с общей теорией относительности Эйнштейна; это приводит к кажущемуся смещению во внешнем направлении звезды у края диска, равному 1",75.

В обоих последних случаях смещение обратно пропорционально расстоянию от звезды до Солнца, причем в случае 3 оно ровно в 2 раза больше, чем в случае 2.

Отметим, что и в случае 2, и в случае 3 предполагается, что гравитационное поле действует на свет точно так же, как и на обычное вещество. Разница же в том, что в случае 2 предполагается справедливость закона Ньютона, а в случае 3 — нового закона тяготения Эйнштейна. Небольшое отклонение от закона Ньютона, которое по теории Эйнштейна приводит к добавочному смещению перигелия Меркурия, возрастает с ростом скорости, пока не удваивает кривизну траектории при достижении предельной скорости — скорости света.

2. Смещение 2 было впервые вычислено проф. Эйнштейном [Einstein A., Ann. Phys., 35, 898 (1911) (перевод: Эйнштейн А. Собрание научных трудов, т. I, «Наука», М., 1965, стр. 165)] в 1911 г. на основе принципа эквивалентности, который состоит в том, что гравитационное поле неотличимо от фиктивного поля сил, создаваемого ускорением системы отсчета. Но даже независимо от того, верен ли общий принцип эквивалентности, были основания полагать, что гравитационное поле должно оказывать воздействие на электромагнитную энергию луча света, особенно после того, как было доказано, что содержащаяся в уране энергия радиоактивности подвержена гравитационному воздействию. Однако в 1915 г. Эйнштейн обнаружил, что общий принцип эквивалентности требует модификации закона тяготения Ньютона и что новый закон приводит к смещению 3.

3. Единственную возможность наблюдать эти предполагаемые отклонения дает луч света от звезды, проходящей около Солнца. (Максимальное отклонение в поле Юпитера составляет всего лишь 0",17.) Очевидно, что наблюдение необходимо проводить во время полного солнечного затмения.

Сразу же после того, как Эйнштейн впервые опубликовал указанное значение, этим занялся д-р Фрейндлих, который попытался извлечь нужную информацию из уже имеющихся снимков солнечных затмений; но ему не удалось собрать достаточно полных данных. Различные исследователи планировали проверку этого эффекта при последующих затмениях, но все такие планы остались невыполненными из-за наличия облачности или по другим причинам [Первая экспедиция по проверке отклонения света во время солнечного затмения была направлена уже в 1914 г. на территорию России. Но в связи с началом военных действий первой мировой войны немецкая экспедиция была интернирована.— Прим. ред.]. После того как появилось второе значение, вычисленное Эйнштейном, экспедиция Ликской обсерватории пыталась наблюдать этот эффект во время затмения 1918 г. Окончательные результаты пока еще не опубликованы. О некоторых результатах их предварительного анализа сообщалось в печати [Observatory, 42, 298 (1919)], но в целом затмение было неблагоприятным и из опубликованных данных вытекает, что вероятная случайная ошибка слишком велика и потому точность измерений недостаточна для выбора между тремя альтернативами.

4. Результаты наблюдений, о которых идет речь в нашей статье, по-видимому, вполне определенно указывают на третью альтернативу и подтверждают общую теорию относительности Эйнштейна. Как хорошо известно, эта теория подтверждается также смещением перигелия Меркурия, которое превышает ньютоновское значение на 43" в столетие, что практически совпадает с тем значением, которое дает теория Эйнштейна. В то же время его теория предсказывает смещение в красную область фраунгоферовых линий на Солнце, достигающее приблизительно 0,008 Å в фиолетовой области. По сообщению д-ра Сент-Джона [St. John, Astrophysical Journ., 46, 249 (1917)] наличие этого смещения не подтвердилось. Если факт этого несоответствия будет принят как окончательный, то это потребует значительных модификаций теории Эйнштейна, которые выходят за рамки нашей темы. Но независимо от того, нужны ли изменения в других частях теории, сейчас, по-видимому, можно считать установленным, что закон тяготения Эйнштейна правильно дает отклонения от закона Ньютона как для сравнительно медленно движущейся планеты Меркурий, так и для быстро движущихся световых волн.

По-видимому, не вызывает сомнения, что найденный здесь эффект обусловлен гравитационным полем Солнца, а не, например, рефракцией в веществе солнечной короны. Чтобы получить наблюдаемый эффект за счет рефракции, необходимо, чтобы Солнце было окружено веществом с показателем преломления, равным 1 + 0,00000414/r, где r — расстояние от центра в единицах солнечного радиуса. На высоте одного радиуса от поверхности требуемый показатель преломления 1,00000212 соответствует показателю преломления воздуха, находящегося под давлением V14o, водорода — под давлением 1/60 или гелия — под давлением 1/20 атмосферного. Ясно, что о плотности такого порядка не может быть и речи.

II. Подготовка к экспедициям.

5. В марте 1917 г. было опубликовано сообщение [Monthly Notices Roy. Astr. Soc, 72, 445 (1917)] о том, что, как показало изучение фотографий, полученных при помощи гринвичского астрографического телескопа во время затмения 1905 г., этот инструмент пригоден для фотографирования звездной карты в окрестности Солнца в период полного затмения. При этом указывалось также, что очень важно провести наблюдения за затмением 29 мая 1919 г., поскольку оно представляет собой особенно благоприятный случай, когда в поле наблюдения оказывается необычное число ярких звезд, который не повторится в течение многих лет.

III. Экспедиция в Собрал. <...>

IV. Экспедиция на Принсипи. <...>

V. Общие выводы.

39. При окончательном анализе всех результатов двух экспедиций наиболее значимыми следует считать те из них, которые получены при помощи четырехдюймового объектива в Собрале. Учитывая более высокое качество изображений и более крупный масштаб фотографий, мы пришли к выводу, что эти снимки должны быть гораздо более надежными. Кроме того, согласие в результатах, независимо полученных из данных о прямых восхождениях и склонениях, а также в ошибках измерения положения на фотопластинках звезд [Phil. Trans. Roy. Soc, ser. A, 220, 308 (1920)] обеспечивают более удовлетворительную проверку результатов измерений, чем было возможно для других инструментов. Полученные фотопластинки дают на основании склонений 1",94, на основании прямых восхождений 2",06.

Результат, основанный на данных о склонениях, должен быть взят с приблизительно вдвое большим весом, чем результат, основанный на данных о прямых восхождениях, поэтому их среднее равно 1",98 с вероятной ошибкой около +0",12.

Наблюдениям на Принсипи сильно мешала облачность. Правда, неблагоприятные обстоятельства частично компенсировались преимуществом крайне постоянной температуры на этом острове. Полученное там отклонение равно 1",61. Вероятная ошибка равна приблизительно ±0",30, так что вес этого результата значительно меньше, чем предыдущего.

Оба эти результата указывают на полное отклонение 1",75, соответствующее общей теории относительности Эйнштейна, причем результаты, полученные в Собрале, указывают на это вполне определенно, а результаты, полученные на Принсипи,— возможно, с некоторой неопределенностью. Правда, остаются еще фотопластинки из Собрала, которые дали отклонение 0",93, отличающееся от указанного значения на величину, намного превышающую случайную ошибку. По причинам, которые подробно разбирались выше, этому результату был приписан малый вес. Было принято, что смещение обратно пропорционально расстоянию от центра Солнца, поскольку все теории согласуются в этом; и действительно из анализа размерностей прямо явствует, что, если смещение обусловлено гравитацией, оно должно изменяться по такому закону.

Данные, полученные с четырехдюймовым объективом, позволяют в какой-то мере проверить этот закон, хотя такая проверка может быть лишь весьма грубой. Соответствующие данные представлены ниже в таблице и (на диаграмме 2) в виде графика зависимости радиальных смещений отдельных звезд (усредненных по всем фотопластинкам) от обратного расстояния до центра. На графике жирной линией отмечены смещения, соответствующие теории Эйнштейна, пунктиром — соответствующие закону Ньютона, а тонкой линией — соответствующие данным наших наблюдений.

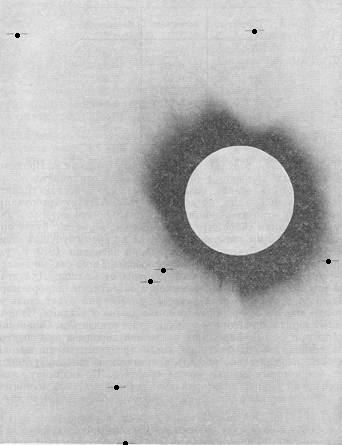
Негатив, полученный с помощью четырехдюймового телескопа, установленного в Собрало (черными точками отмечено положение звезд при полном солнечном затмении 1919 года).

Радиальные смещения отдельных звезд

Звезды	Вычисления	Наблюдения
11	0",32	0",20
10	0",33	0",32
6	0",40	0",56
5	0",53	0",54
4	0",75	0",84
2	0",85	0",97
3	0",88	1",02

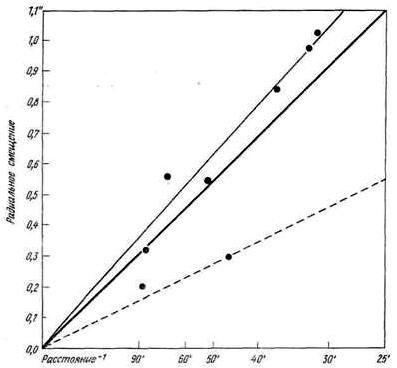
Диаграмма 2

Таким образом, результаты экспедиций в Собрал и на Принсипи оставляют мало сомнения в том, что луч света отклоняется вблизи Солнца и что отклонение, если приписать его действию гравитационного поля Солнца, по величине соответствует требованиям общей теории относительности Эйнштейна. Однако интерес к данным наблюдениям таков, что в дальнейшем, вероятно, будет признано желательным еще раз провести их во время будущих затмений. Необычайно благоприятные условия затмения 1919 г. уже не повторятся, и придется фотографировать более слабые звезды, которые, вероятно, будут более удалены от Солнца. Для этого пригоден астрографический телескоп с объективом, диафрагмированным до 8 дюймов, если качество фотографий будет столь же высоким, как и в обычной работе со звездными объектами. От цело-статных зеркал, по-видимому, лучше будет отказаться. Они весьма удобны при фотографировании солнечной короны и при спектроскопических наблюдениях, но когда требуется очень высокая точность, нежелательно вводить в оптическую систему усложнения, без которых вполне можно обойтись. По-видимому, здесь нужен некий вариант экваториальной установки (такой, например, как применявшаяся в экспедициях Ликской обсерватории по изучению солнечного затмения)» [13, с. 564 – 570].

– VI –

Известие о благоприятном исходе для ОТО Эйнштейн узнал в начале сентября 1919 года. После публикации в лондонской «Таймс» научно-популярной статьи об искривлении луча света в поле тяготения Солнца, имя Эйнштейна стало известно широкой общественности. В конце этого месяца он отправил открытку в Швейцарию, в которой писал: «Дорогая Мама! Сегодня я получил радостное известие. Х.А. Лоренц телеграфировал мне, что английские экспедиции действительно доказали отклонение света вблизи Солнца…» [14, с. 113].

Что творилось в ученом мире Великобритании в ноябре 1919 года, лучше всего передать словами Абрахама Пайса:

«После 1905 г., совершив два первоклассных чуда, Эйнштейн стал "блаженным". Состоявшееся 6 ноября 1919 г. совместное заседание Королевского общества и Королевского астрономического общества напоминало обряд конгрегации. В качестве постулатора выступал Дайсон, которому помогали адвокаты-прокураторы Кроммелии и Эддингтои. Выступавший первым Дайсон в заключение сказал: "После тщательного изучения фотопластинок я готов заявить, что расчеты Эйнштейна подтверждены. Получен совершенно определенный результат, в соответствии с которым свет отклоняется согласно закону тяготения Эйнштейна".

С дальнейшими разъяснениями выступил Кроммелин, после чего слово взял Эддингтон, заявивший, что результаты, полученные на Принсипи, подтверждают данные экспедиции в Собраль, и перечислил два несомненно установленных чуда, сотворенных Эйнштейном уже в ранге "блаженного": объяснение смещения перигелия Меркурия и искривления лучей света па угол (1,98 ± 0,30)" и (1,61 ± 0,30)"; такие результаты были получены соответственно в Собрале и на Принсипи.

"Адвокат дьявола" Людвик Зильберштейн выдвинул критические замечания: "Пока нет достаточных оснований утверждать, что искривление лучей света, наличие которого я признаю, вызывается тяготением". Он также требовал подтвердить наличие красного смещения: "Если красное смещение не удастся обнаружить (как было до сих пор), вся теория рухнет". Указывая на висящий в зале портрет Ньютона, Зильберштейн воззвал к конгрегации: "Память об этом великом человеке заставляет нас с огромном осторожностью относиться к попыткам изменить или полностью пересмотреть его закон тяготения".

Председательствовавший на заседании президент Королевского общества кавалер ордена "За заслуги" Джозеф Джон Томсон, выслушав петицию "instanter, instantius, instantissime", провозгласил буллу канонизации: "Это самый важный результат, полученный в теории тяготения со времен Ньютона, и весьма символично, что о нем объявлено на заседании общества, столь тесно связанного с именем великого ученого... Этот результат — одно из высочайших достижений человеческого разума".

Спустя несколько недель он добавил: "Обнаружение отклонения лучей света веществом, которое предполагал еще Ньютон в своем первом Вопросе [вынесен в эпиграф к § 11.2.— Пер.], само по себе было бы научным результатом первостепенного значения; сейчас это событие приобретает еще большую важность, потому что значение отклонения подтверждает закон тяготения, открытый Эйнштейном"… Так, с 7 поября 1919 г. начала создаваться легенда об Эйнштейне» [10, с. 292 – 293].

Однако тот же Дж. Дж. Томсон писал: «Я должен признаться, что никому еще не удалось выразить ясным языком, что в действительности представляет собой теория относительности Эйнштейна». Это откровение самого именитого физика Британии привел Б.Г. Кузнецов [16, c. 184], который, в свою очередь, взял его из биографии Эйнштейна, написанной Ф. Франком. Увы, официальная история физики пока пишется релятивистами, и мы не знаем истинного раздражения Дж. Дж. Томсона теорией относительности. Известно лишь, что ни СТО, ни ОТО он не принял, поскольку всю жизнь разрабатывал конструктивную теорию движущегося электрона, основанную на механической модели, в противовес формалистским теориям Эйнштейна, Лоренца и Пуанкаре, базирующихся на пространственно-временных спекуляциях.

Горожане на улице Нью-Йорка радостно приветствуют Эйнштейна. Основная цель его поездки в США (совместно с Х. Вейсманом) — сбор средств для строительства Иерусалимского университета. Он пробыл в Америке со 2 апреля по 30 мая 1921 года. За это время он прочел несколько популярных лекций по теории относительности в Чикаго, Бостоне и Принстоне, в Вашингтоне удостоился чести встретиться с президентом страны Гардингом. На обратном пути из Америки он останавливается в Англии и посещает могилу Ньютона.

Вообще, релятивистское учение не пользовалось большой популярностью у англичан, поскольку в их стране была слишком сильна классическая школа, заложенная Фарадеем и Максвеллом. Но после популяризации ОТО английскими астрономами, — Дайсоном, Кроммелиным и, особенно, Эддингтоном — положение дел существенно изменилось, правда, не в теоретическом плане. Рассказывают, что некий собеседник Эддингтона утверждал, будто входит в число трех ученых, которые действительно понимают теорию относительности Эйнштейна. Эддингтон задумался, а когда собеседник спросил его, над чем тот размышляет, Эддингтон ответил: «Я спрашиваю себя, кого вы имели в виду третьим».

Эйнштейн и Эльза в Японии. 8 Октября 1922 года он вместе с женой выехал из Марселя на Дальний Восток. Во время этой поездки он посетил Коломбо, Сингапур, Гонконг и Шанхай. В Японии он был с 17 ноября по 29 декабря. 9 Ноября ему присуждена Нобелевская премия. 10 Декабря в Стокгольме на торжественном вручении премии Эйнштейна представлял посол Германии Рудольф Надольны. На обратном пути из Японии Эйнштейн совершает 12-дневную поездку по Палестине, куда он пребывает 2 февраля 1923 года.

«Своей внезапной славой, — писали авторы "Частной жизни", — Эйнштейн обязан сочинителям эффектных заголовков для английский и американских газет. "Революция в науке", "Новая теория строения вселенной", "Ниспровержение механики Ньютона" — захлебывалась лондонская "Тамс" 7 ноября 1919 года. "Лучи изогнуты, физики в смятении. Теория Эйнштейна торжествует, — объявила "Нью-Йорк таймс" двумя днями позже» [15, с. 246]. В декабре 1919 году Эддингтон написал Эйнштейну: «...Вся Англия только и говорит о Вашей теории. Она произвела потрясающую сенсацию... Ничего лучшего с точки зрения научных связей между Англией и Германией и пожелать нельзя» [14, с. 114].

8 Феврале 1923 года Эйнштейн становится первым почетным гражданином Тель-Авива. Летом этого года он помогает основать общество «Друзей Новой России», которое просуществовало 10 лет. В следующем году он становится членом еврейской общины Берлина и регулярно платит взносы. В Потсдаме начинает работать «Институт Эйнштейна», расположенный в «Башне Эйнштейна», в которой установлен «телескоп Эйнштейна».

Помощник Эйнштейна, польский математик Леопольд Инфельд, следующим образом обосновывал оглушительный успех у публики теории относительности. Рассказав о «великом предвидении», подтвердившемся в мае 1919 года, он написал:

«Так началась великая слава Эйнштейна. Она продолжалась в течение всей его жизни и, вероятно, будет лишь возрастать после его смерти. Однако тот факт, что теория относительности предсказала явление, столь же далёкое от нашей повседневной жизни, как эти звёзды, что она предвидела его на основании длинной цепи абстрактных аргументов — всё это не может, пожалуй, служить достаточным поводом для массового энтузиазма. Тем не менее, дело обстояло именно так. И мне кажется, что причины тут следует искать в послевоенной психологии.

Это произошло после окончания первой мировой воины. Людям опротивели ненависть, убийства и международные интриги. Окопы, бомбы, убийства оставили горький привкус. Книг о войне не покупали и не читали. Каждый ждал эры мира и хотел забыть о войне. А это явление способно было захватить человеческую фантазию. С земли, покрытой могилами, взоры устремлялись к небу, усеянному звездами. Абстрактная мысль уводила человека вдаль от горестей повседневной жизни. Мистерия затмения Солнца и сила человеческого разума, романтическая декорация, несколько минут темноты, а затем картина изгибающихся лучей — все гак отличалось от угнетающей действительности.

Существовала и еще одна причина, видимо, важнейшая: новое явление предсказал немецкий ученый, а проверили его английские ученые. Физики и астрономы, принадлежавшие недавно к двум враждебным лагерям, снова работают вместе. Может быть, это и есть начало новой эры, эры мира? Тяга людей к миру была, как мне кажется, главной причиной возрастающей славы Эйнштейна» [17, с. 154 – 155].

Эту же мысль высказали авторы «Частной жизни», присовокупив к сказанному Инфельдом еще один немаловажный фактор — обаяние личности отца-основателя волшебной теории:

«Люди устали от войны, им хотелось отвлечься, и теория относительности стала темой номер один, сенсацией для массового читателя. Искривленное пространство и отклонение световых лучей были у всех на устах, эти слова, что бы они ни значили, завораживали публику. Всякому, кто когда-либо смотрел на ночное небо, оно казалось волшебным и полным тайн, и вот внезапно эти тайны оказались раскрытыми...

Разумеется, репортеры ринулись выяснять, какой человек стоит за новой сенсацией. И обнаружили, что им необычайно повезло. Вместо типичного седовласого академика их взору, предстал эксцентричный тип со всклокоченными волосами, дерзким обаянием и чувством юмора, переходящим в сарказм. Эйнштейн оказался эффектной и колоритной фигурой, он был фотогеничен, и вскоре представители прессы при каждом удобном и неудобном случае стали забрасывать его вопросами на самые неожиданные темы. "От меня хотят статей, заявлений, фотографий и пр., — писал он на Рождество 1919 года. — Все это напоминает сказку о новом платье короля и отдает безумием, но безобидным". Он вскоре ощутил себя Мидасом, но все, к чему он прикасался, обращалось не в золото, а в газетную шумиху.

Средства массовой информации создали Эйнштейну имидж мудреца и оракула, и теперь его внимания домогался весь мир. В течение следующих десяти лет он побывал в Скандинавии, в Соединенных Штатах Америки, в Японии, на Ближнем, Среднем и Дальнем Востоке, в Южной Америке и в Великобритании, где известный лондонский эстрадный театр "Палладиум" предложил ему сцену, чтобы он три недели вел собственную программу, а дочь Лорда Холдейна, под чьим кровом Эйнштейну предстояло жить, при встрече с ним упала в обморок.

Во время поездки в Женеву его осаждали толпы молодых девиц, одна из них даже попыталась вырвать у него прядь волос. В его честь называли сигары, младенцев, телескопы и башни, непрерывным потоком шли письма. Этому не суждено было иссякнуть никогда. Кто только не писал Эйнштейну: доброжелатели, религиозные психопаты, шарлатаны, просившие денег, общественные организации и движения, искавшие его поддержки, школьники и, наконец, одна маленькая девочка, задавшая вопрос: "А вы действительно есть?"» [15, с. 247 – 249].

Человечество ненавидит разоблачителей религиозных культов, оно проклинает ученых, которые берутся доказывать не божественное происхождение Иисуса Христа. Но мы-то с вами, дорогой читатель, не религиозные люди и должны понимать, откуда проистекает «Истина» учения «Святого Альберта». Пусть в Израиле продолжают праздновать «День Науки» в день рождения Эйнштейна — 14 марта. Но нам россиянам, исследователям физического мира, не к чему вечно стоять у алтаря релятивистской церкви. Пора бы, наконец, погасить свечи, зажженные в эпоху явления народам Мессии. Пусть простой люд томится в ожидании второго пришествия, служителям науки нужно подумать над иным, не религиозным, объяснениям искривления лучей.

Критики результатов наблюдений указывают, что Эддингтон был слишком заинтересован в успехе теории относительности и потому не был объективен в отношении оценки экспедиции. В своем отчете, говорят они, он игнорировал звезды, отклонения которых не вписывались в нужные ему рамки. В Интернете можно найти, например, вот такие слова: «Эддингтон ограничился устным заявлением о верности ОТО, но не опубликовал ни анализа погрешностей, ни полученных им фотографий, ни методики отбраковки тех из них, которые были расценены как "плохие"». Из процитированного только что отчета следует, что это, мягко выражаясь, не совсем верно.

В отчете (п. 39) есть определенные указания на то, что

«При окончательном анализе всех результатов двух экспедиций наиболее значимыми следует считать те из них, которые получены при помощи четырехдюймового объектива в Собрале. … Полученные фотопластинки дают на основании склонений 1",94, на основании прямых восхождений 2",06». И далее: «Наблюдениям на Принсипи сильно мешала облачность. Правда, неблагоприятные обстоятельства частично компенсировались преимуществом крайне постоянной температуры на этом острове. Полученное там отклонение равно 1",61. Вероятная ошибка равна приблизительно ±0",30, так что вес этого результата значительно меньше, чем предыдущего».

Тем не менее, в Интернете бесконечное число раз цитируются дневниковые записи Эддингтона, находящегося в момент затмения на Принсипи, а именно следующее место:

«…Дождь окончился около полудня и примерно в 1 : 30 мы увидели Солнце. Мы приготовили наши фотоаппараты, надеясь на случай. Я не видел самого затмения, будучи очень занят меняя фотопластинки, кроме одного взгляда, чтобы удостовериться, что оно началось, и полу-взгляда, чтобы оценить количество облаков. Мы получили 16 снимков, на которых Солнце получилось со всеми деталями, но облака закрывали звёзды. На последних нескольких снимках было несколько изображений звёзд, которые дали нам то, что нам было нужно …» [взято из Википедии, Эддингтон].

Таким образом, у читателя этих строк создается превратное впечатление, будто из-за облачности проверка ОТО полностью провалилась. Это, конечно, не так. Известна телеграмма руководителя экспедиции в Собраль, которую никогда не цитируют критики: «Затмение превосходно. Кроммелин» [10, с. 291]. Так что если бы Эддингтон затмения в Принсипи вообще не наблюдал, результаты всё равно бы у него имелись.

Однако, можно ли выводы по результатам наблюдений 1919 года считать абсолютно безупречными с точки зрения экспериментальной науки 2009 года? Ни в коем случае, отвечает Геннадий Ивченков. Он утверждает, что и 90 лет тому назад, Эддингтон со своими товарищами поторопился с позитивной оценкой, подтверждающей ОТО.

Он уверен, что точность измерения порядка 0.1" ÷ 0.2" трудно достижима даже в начале 21-го века, о начале 20-го и говорить не приходится.

«При проведении измерений с такой точностью, — пишет Ивченков, — неизбежно "выплывает" большое число источников ошибок, систематических и случайных, которыми ранее, при измерении с точностями порядка 1", можно было пренебречь. Необходимо отметить, что современные астрометрические приборы, имеющие точность порядка секунды — всегда прецезионно-калиброванные с термостабилизированной камерой» [12].

Далее он почему-то навскидку оценивает диаметр объектива:

«Экспедиция была выездная, следовательно, они не могли взять телескоп с диаметром объектива, превышающим, например, 500 мм... По-видимому, диаметр зеркала телескопа не превышал 200 ÷ 300мм. Теоретическое значение кружка рассеяния для 300 мм телескопа равно 0.8", а разрешающая способность (теоретическая, по Рэлею) — 0.4"» [12, п. 1].

Однако достоверно известно, что основной массив данных был получен с помощью четырехдюймового телескопа (т.е. чуть более 100 мм), установленного в Собрале. Следовательно, по расчетам Ивченкова, точность показаний должна быть намного хуже одной угловой секунды.

Следующей неприятной помехой при наблюдении звезд во времая затмения Ивченков называет дисторисию, разъясняя ее действие словами нашего отечественного авторитета:

«Дисторсия обычно не вредит наблюдателю, но становится очень опасной, если при помощи оптической системы производятся съемки, предназначенные для промеров (например, в геодезии или, особенно, в аэрофотограммометрии)". (Г. С. Ландсберг "Оптика" стр.309)».

Критик продолжает:

«Нескомпенсированная дисторсия приводит к подушко-образным искажениям, создавая впечатление выпуклого или вогнутого поля зрения. Таким образом, в первом случае звезды как бы разбегаются от центра, а во втором — сбегаются. Пока никому не удавалось скомпенсировать, в частности, дисторсию до суб-секундных значений даже для малых углов зрения. Таким образом, если использовать оптическую систему с нескомпенсированной дисторсией, то можно увидеть (и даже успешно измерить) всю кривизну метрики пространства-времени» [12, п. 2].

За дисторисией Ивчинков указал на явление гидирования:

«Если во время экспозиции не использовался гидирующий механизм, компенсирующий суточное движение, то за 10 - 20 сек. экспозиции кружки рассеяния превращались в эллипс, вытянутый на 2,5 - 5' по эклиптике. Если этот механизм использовался, то очень сомнительно, что он имел суб-секундную точность» [12, п. 3].

По оценке Ивчинкова, ошибка, вызванная гидированием, составит приблизительно 0.3".

Четвертым пунктом идет рефракция в атмосфере Земли:

«Опорная фотопластинка была снята в январе в Англии (угол эклиптики над горизонтом - 20 град.), а затмение снималось на экваторе в 13 : 30, т.е. Солнце было в зените. Атмосферная рефракция при угле 10 град. над горизонтом составляет 5' 30", при угле 20 град. — 2'40", а в зените близка к нулю (см. таблицы Пулковской Обсерватории). Следовательно, в 4 град поле зрения (между 20 и 10 град азимута) присутствовала нелинейность порядка 80 ÷ 100", искажающая (растягивающая) вертикальный масштаб» [12, п. 4].

Ниже автор статьи «Самое важное подтверждение ОТО или Что измерил лорд Эддингтон в 1919 году» проанализировал:

5. Звездную аберрацию.
6. Собственное движение звезд.
7. Точность, обеспечиваемая фотоматериалами в данных условиях.
8. Точность совмещения пластинок.
9. Точность считывания результатов.
10. Общие замечания по поводу применения фотоматериалов для анализа изображения.

После этого Ивчинков перечислил основные методические ошибки эксперимента:

• отсутствие калибровки телескопа и камеры,
• съемка опорной пластинки в другом месте,
• использование широкоугольного телескопа,
• использование неденситометрированных фотоматериалов низкого качества,
• ручная ("на глаз") обработка изображений.

Самыми грубыми и принципиальными из них являются последние три. Применение широкоугольного телескопа привело к необходимости измерения крайне малых линейных величин, а сами эти измерения были выполнены варварским методом.

Претензии, высказанные здесь, нужно, конечно, принять во внимание: указанные факторы, несомненно, могли повлиять на окончательные выводы представленного отчета. Ивчинков мог упустить из виду какие-то частности, но при этом он остается прав в главном: оптические явления, происходящие вблизи Солнца настолько сложны, что чисто гравитационные объяснения микроскопических отклонений лучей от звезд выглядят просто смехотворно.

Задайте себе вопрос: почему мы до сих пор обсуждаем результаты почти вековой давности? Где данные по самым последним затмениям Солнца? Если их нет в справочниках по наблюдательной астрономии, в которых из года в год вносятся уточнения по тем или иным параметрам, — значит, отклонения лучей вблизи массивных тел абсолютно не интересуют астрономов-практиков, и мы догадываемся почему.

---

1. Эйнштейн А. Собрание научных трудов в 4-х томах. / Под ред. И.Е. Тамма, Я.А. Смородинского и Б.Г. Кузнецова. — М.: Наука, 1965.
2. Паунд Р.Ф. О весе фотонов. / УФН LXXII вып. 4 (1960).
3. Окунь Л.Б., Селиванов К.Г., Телегди В. Гравитация, фотоны, часы. / УФН 169 (1999).
4. Soldner, J. G. v. "Ueber die Ablenkung eines Lichtstrahls von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkörpers, an welchem er nahe vorbei geht". Berliner Astronomisches Jahrbuch (1804) s. 161 – 172.
5. Soldner, J. G. v. "Ueber die Ablenkung..." ; (Lenard, P.) (1921). Annalen der Physik 65: 593 – 604.
6. Jaki, S.L. (1978). "Johann Georg von Soldner and the Gravitational Bending of Light, with an English Translation of His Essay on It Published in 1801". Foundations of Physics 8: 927–950. doi:10.1007/BF00715064..
7. Treder, H. J.; Jackisch, G. (1981). "On Soldners Value of Newtonian Deflection of Light". Astronomische Nachrichten 302: 275–277. doi:10.1002/asna.2103020603.
8. Will, C.M. (1988). "Henry Cavendish, Johann von Soldner, and the deflection of light". Am. J.Phys. 56: 413–415. doi:10.1119/1.15622.
9. Захаров А.Ф. Гравитационные линзы / Соровский образовательный журнал, том 7, № 8, 2001; его же книга "Гравитационные линзы и микролинзы" М.: Янус, 1997.
10. Pais A. Subtle is the Lord... The Science and the Life of Albert Einstein (Oxford: Oxford Univ. Press, 1982). [Русск. пер.: Пайс А. Научная деятельность и жизнь Альберта Эйнштейна. — М., 1989].
11. Тимирязев А.К. Теория относительности Эйнштейна и диалектический материализм / «Под Знаменем Марксизма» 1924 г., № 8–9, с. 142 – 157; № 10–11, с. 93 — 114; его же Теория относительности Эйнштейна и махизм / Стенограмма доклада на заседании Комм. Акад. — 7/II 1924 г. // Опубликована в сборнике статей «Естествознание и диалектический материализм». — М.: Материалист, 1925, с. 228–258; его же книга "Введение в теоретическую физику". — М.- Л.: ГТТИ, 1933.
12. Ивченков, Геннадий. Самое важное подтверждение ОТО, или Что измерил лорд Эддингтон ( http://bourabai.kz/articles/ivchenkov.htm ).
13. Альберт Эйнштейн и теория гравитации / Сборник статей. — М.: Мир, 1979.
14. Хофман Б., Дюкас Э. Альберт Эйнштейн. Творец и бунтарь. — М.: Прогресс, 1983. (Banesh Hoffmann/Helen Dukas: Einstein. Schopfer und Rebell . Die Biographie, Frankfurt/M. 1978, amerikanisches Original New York, Viking Press, 1972).
15. Картер П., Хайфилд Р. Эйнштейн. Частная жизнь. — М.: «Захаров», 1998 (Paul Carter and Roger Highfield «The Private Lives of Albert Einstein», 1993).
16. Кузнецов Б.Г. Эйнштейн. Жизнь. Смерть. Бессмертие. Издание пятой, переработанное и дополненное. / Под редакцией М.Г. Идлиса. — М.: Наука, 1980.
17. Инфельд, Леопольд. Мои воспоминания об Эйнштейне / УФН, Т. LIX, вып. 1, 1956; «Tworczosc», вып. 9, 1955 г.; перевод с польского И.Е. Дудовской и Г.И. Залуцкого.
18. Петров А.М. Антиэйнштейн, — М.: Компания спутник, 2008.
19. Струве О., Линдс Б., Пилланс Э. Элементарная астрономия. — М.: "Наука", 1967.
20. Талызин, Игорь. Смещение звёзд во время затмения 1922 года ( http://lesage.narod.ru/Sun1922_2007.htm ).
21. Адам М.Г. Экспериментальные проверки теории гравитации. - в кн. Эйнштейновский сборник, 1969-1970. М.: Наука, 1970, с.196. ( http://www.lesage.narod.ru/Mikhailov/Sun.htm ).