Критика теории относительности

Олег Акимов

13. Аномальное движение перигелия Меркурия

– I –

Урбен Жан Жозеф Леверье (1811 — 1877), директор Парижской обсерватории, специалист в области небесной механике, в свое время исследовал неправильности в движении Урана и на основании своих наблюдений, независимо от Дж. К. Адамса, рассчитал орбиту новой планеты, которая была в 1846 г. открыта Г. Галлем и названа Нептуном. Еще в 1839 г. Леверье представил расчеты взаимных возмущений для всех планет и доказал устойчивость движений Солнечной системы. В 1859 г. он пришел к заключению о существовании аномального смещения перигелия Меркурия, которое в то время невозможно было объяснить с точки зрения законов небесной механики.

Саймон Ньюком (1835 — 1909), ведущий сотрудник Морской обсерватории в Вашингтоне, профессор математики в Морской академии, занимающийся составлением точных таблиц движения планет, подверг вычисления Леверье тщательной проверке. В 1895 г. им были опубликованы данные по движению ближайших к Солнцу четырех планет. С помощью формулы Холла для всемирного закона тяготения Ньюкому удалось подогнать расчетные данные к эмпирическим. Для формулы Холла, имеющую вид: F = GMm / r ^{(2 + δ)}, он нашел δ = 161,2 · 10 ^–9. При этой поправке ему удалось ликвидировать невязку для Меркурия, равную примерно 42 угловых секунды в столетие. Недостатком его подгонки было то, что поправка δ для разных планет оказывалась различной. По сути, он прибег к птолемеевской методологии, при которой все внимание сосредоточено не на физике астрономических явлений, а на возможности прогнозировать числовые параметры Солнечной системы.

В середине прошлого века Джеральд Клеменс (1908—1974) вместе с Дирком Брауэром (1902—1966) провел большую серию прецизионных измерений планетных траекторий и сравнил их с теоретическими значениями, причем в его работе были впервые применены компьютеры. Согласно его расчетам получились следующие наблюдаемые вековые смещения планетных перигелиев (в скобках даны эти же величины, рассчитанные по ОТО):

Меркурий — 43,11 ± 0,45 (43,03),
Венера — 8,4 ± 4,8 (8,6),
Земля — 5,0 ± 1,2 (3,8),
Марс — 1,1 ± 0,3 (1,4).

Как видим, по ОТО согласие по Земле и особенно по Венере — неважное. Однако при расчете столь малых поправок многое зависит от постановки многофакторной задачи (Ньюком удерживал в заданных пределах полтора десятка факторов). Если ориентироваться на ОТО — а такая задача стояла на повестке дня, — то нужные результаты можно было бы получить путем варьирования других параметров, например массы планет. Если бы стояла задача строгого подтверждения всех масс планет, то можно было бы слегка «отпустить» вековые смещения перигелиев орбит. Совершенно недопустимо брать параметры из разных систем расчета, например, Ньюкома (1898), Брауэра — де Ситтера (1948), Клеменса (1964), а такое изредко делают авторы популярных книг.

Известный популяризатор наблюдательной астрономии, крупный специалист по кометам В.А. Бронштэн (1918 — 2004) пишет: «До самого конца XIX века не существовало единой системы фундаментальных астрономических постоянных. Каждый астроном выбирал те значения постоянных, которые представлялись ему наиболее заслуживающими доверия. Лишь в 1895 г. Саймон Ньюком, проделав титаническую работу по обработке и анализу 60000 меридианных наблюдений, планет, Солнца и Луны (эта работа заняла у него 18 лет), предложил взаимно согласованную систему из 14 астрономических постоянных. Эта система продержалась в науке почти 70 лет: с 1896 г., когда она была официально утверждена на международной астрономической конференции в Париже, до 1964 г., когда XII съезд Международного астрономического союза в Гамбурге утвердил новую систему» [10, гл. V], которая во многом строилась на данных Клеменса и других астрономов, использующих машинный расчет.

– II –

Следует отметить, что при рассмотрении больших масс, какую имеет Солнце, не только Ньюком предлагал слегка подправить формулу всемирного тяготения, но и другие исследователи. Например, Абрагам выдвинул теорию, согласно которой гравитационная сила изменялась по закону: F = A / r ² + B / r ³, причем B / A = GM / 2c ², где M — масса центрального тела. Мы не знаем, чем руководствовался Абрагам, когда записывал таким образом формулу, но у нас нет никаких сомнений в том, что закон всемирного тяготения, записанный для двух материальных точек в виде F = GMm / r ², должен изменить свой вид, когда рассматриваются реальные тела, имеющие определенную форму и размеры.

Сегодняшний студент механического факультета в состоянии вывести выражение для силы, которая действует на материальную точку A со стороны эллипсоида (рис. 1). Если принять массу эллипсоида за M, массу материальной точки A за единицу m = 1, задать экваториальную (a) и полярную (b) полуоси эллипсоида, ввести высоту h и центральный радиус-вектора r точки A, то формула для нахождения результирующей силы F, действующей на точку A, будет выглядеть следующим образом [1, с. 55]:

.

Рис. 1. Притяжение материальной точки A массивным эллипсоидом, который имеет заметно большие размеры по сравнению с удаленностью точки A, будет отличаться от привычного закона всемирного тяготения, выведенного для случая двух материальных точек.

Итак, силовая функция зависит от геометрии масс. Вместо силы F удобно воспользоваться гравитационным потенциалом U. При перемещении конца радиуса-вектора r на расстояние dr сила тяготения F, действующая на тело с массой m, совершает работу: dA = –Fdr. При перемещении массы m из точки P₁ с радиусом r₁ в точку P₂ с радиусом r₂ работа сил тяготения будет равна:

.

Гравитационный потенциал точки P₁ определяется как работа против сил поля по перенесению массы m из точки P₁ с радиусом r₁ в бесконечно удаленную точку P₂ = ∞, где потенциал равен нулю (U₂ = 0):

.

На элемент массы dm определенных размеров и формы со стороны центрального тела M действует сила, описываемая силовой функцией dU. В литературе [2, с. 10] и [3, с. 25] можно найти вывод интеграла силовой функции U по объему V тела m, в роли которого чаще всего выступает сфера или эллипсоид:

,             .

Общий вид силовой функции выглядит следующим образом:

где γ₁, γ₂, γ₃, — направляющие косинусы, A, B, C — главные центральные моменты инерции эллипсоида, определяемыми его полуосями a, b и c. «Первый член в выражении отвечает потенциалу материальной точки и дает кеплерову орбиту. Второй и третий члены зависят от протяженности тела и его ориентации и, строго говоря, характеризуют зависимость орбиты от этих факторов. Что касается ориентации тела, то она целиком определяется третьим членом, содержащим направленные косинусы» [2, с. 14]. До сих пор не известно о степени сжатия Меркурия и направленности его оси вращения. Однако известно, что всякое отклонение материальных тел от шаровой формы приводит к так называемому «аномальному сдвигу». Выясним, в чем он заключается.

Если рассматривать только два небесных тела, Меркурий и Солнце, причем идеальной сферической формы, находящихся в абсолютном вакууме и в виде холодных масс, то перигелий планеты, вращающейся по эллипсу вокруг светила, будет находиться в покое, на одном и том же месте в точке P (рис. 2). Но остальные планеты Солнечной системы, а также сжатие светила у полюсов и прочие причины, перечисленные в табл. 1, вносят определенное возмущение в это движение и линия AP, соединяющая ближнюю и дальнюю точку орбиты, медленно перемещается. За сто лет перигелий Меркурия повернется на 5600 угловых секунд; из них 5025" — поворот системы отсчета и 575" — динамическое смещение, обусловленное влиянием объектов Солнечной системы. Эти числа фигурируют в данных по Клеменсу.

Рис. 2. Перигелий (P) орбиты Меркурия, т.е. ближайшая точка к Солнцу (S), перемещается на угол Δφ = 566" за столетие (по Роузверу). Из этой величины сдвиг в 527" можно обосновать с точки зрения классических законов небесной механики; оставшиеся величина в 39" считается аномальным сдвигом.

В табл. 1 приведены причины сдвига и расчетные значения, выполненные тремя авторами в различное время. Во второй графе даны количественные оценки, полученные Лаверье в 1860, в третьей — Клеменсом в 1947 г. [4, с. 325], а третья графа заполнена числами, взятыми из работы Роузвера [5, с. 17] (если величина не рассчитывалась, то в табл. 1 ставился прочерк).

Таблица 1
Возмущения, вызывающие сдвиг перигелия Меркурия
(в секундах дуги за столетие)

Причина сдвига	по Лаверье	по Клеменсу	по Роузверу
Меркурий	—	0.025 ± 0.00	—
Венера	280,64	277.856 ± 0.68	280.6
Земля	83,61	90.038 ± 0.08	83.6
Марс	2,55	2.536 ± 0.00	2.6
Юпитер	152,59	153.584 ± 0.00	152.6
Сатурн	7,24	7.302 ± 0.01	7.2
Уран	0,14	0.141 ± 0.00	0.1
Нептун	0,06	0.042 ± 0.00	—
Сжатие Солнца	—	0.010 ± 0.02	—
Прецессия	—	25.645 ± 0.5	—
Вычисленная сумма	526,83	557.180 ± 0.85	526.7
Данные наблюдения	565,1	599.74 ± 0.41	565.7
Разность	38,3	42.56 ± 0.94	39.0

Можно видеть, что цифры в табл. 1 «гуляют» довольно в широких пределах из-за прецессии (25,6), между тем, аномальный сдвиг очень небольшой. Различие в числовых данных можно объяснить тем, что Клеменс выступал за ОТО, а Лаверье о ней ничего не знал.

– III –

А.К. Тимирязев в связи с подгонкой, выполненной Эйнштейном, писал: «...Формула, выражающая это перемещение, совпадающая с Эйнштейновской, была выведена иным путем Гербером и была уже напечатана в журнале Физики и математики [Zeitschrift fur Mathematik und Physik] в 1898 г., следовательно, за 17 лет до Эйнштейна. Но самое важное не в этом. По формуле Гербера-Эйнштейна получается следующее: перемещение перигелия в сто лет равно 42 секундам дуги (42 секунды дуги, т.е. 42/3600 доли градуса — около одной сотой доли градуса). С другой стороны, обработка астрономических наблюдений, сделанная Леверье и Ньюкомбом, дает 42,2"; казалось бы лучшего совпадения и нельзя ожидать. Однако, и это совершенно естественно для строгой научной работы, — у целого ряда ученых явилась мысль еще раз проверить выводы Леверье и Ньюкомба, и что же оказалось? Оказалось, что расчеты были не совсем точны. Е. Вихерт, тщательно проверивший работу Леверье и Ньюкомба, получил не 42,2", а 34". Гроссман [Zeitschrift fur Physik, 5 том, стр. 280. 1921 г. Astronom. Nachr. 214 p. 41 и 195. 1921 года] также перечислил все астрономические наблюдения, причем он выделил в отдельную группу данные, полученные с помощью меридианного круга. Из этой группы наблюдения получается 29", а если использовать все наблюдения, то по Гроссману получается 38". Результаты этих вычислений никем не опровергнуты. Таким образом, говорить о согласии теории с фактами еще рано, а может быть, и поздно!» [6] (эта работа А.К. Тимирязева имеется у нас на сайте, см. Теория относительности Эйнштейна и диалектический материализм).

В самом деле, в соответствии с табл. 1, разность между двумя вычисленными значениями по Клеменсу и Роузверу составляет 30,5" (= 557,18" – 526.7"), что недопустимо, если разность между вычисленным и наблюденным значениями находится где-то в районе 40". Между тем, в начале века оперировали совершенно другими величинами (их приводит А.К. Тимерязев в своей книге [7, c. 386]), именно: теоретическое значение равнялось 601", а наблюденное — 642,6", их разность равна 41,6". Данная величина как будто бы близка к значению, полученному Клеменсом, но разве мы можем говорить о сходстве ситуаций в этих двух случаях? Разумеется, нет. У Леверье разность составила 38", что близко к значению, полученному Роузвером (39"), но и здесь мы не имеем право говорить о каком-либо согласии, так как уменьшаемые и вычитаемые у них слишком различаются. Эйнштейн получил разность 42,9", что позволило релятивистам громко заявить о триумфе его теории. Однако, какую величину надо брать в качестве наблюденной, если в наших примерах она колеблется от 565,7" до 642,6" ?

И тут мы подходим к основной претензии, предъявляемой Тимерязевым в адрес релятивистов. Как можно, говорит он, вычислять общий сдвиг перигелия Меркурия с позиции классической механики, а неувязку с эмпирическими данными с позиции теории относительности? Если вы хотите остаться в рамках релятивистских представлений, то вам необходимо вести расчет по всем 642,6" (данные А.К. Тимерязева), а не по разности в 43". Подобная методическая ошибка имеет место и в рамках СТО. При вычислении разности хода лучей в горизонтальном и вертикальном плече интерферометра Майкельсона скорость света складывается и вычитается со скоростью движения Земли по обычным формулам сложения скоростей. Однако, получив в эксперименте Майкельсона – Морли нулевой сдвиг интерференционных полос, релятивисты объявляют скорость света неизменной, а релятивистскую формулу сложения скоростей единственно правильной (см. Эксперимент Майкельсона – Морли ). Уважаемые релятивисты, будьте до конца последовательны: не пользуйтесь, пожалуйста, формулой c + v при анализе решающего эксперимента СТО! Та же самая просьба к вам, когда вы имеете дело с ОТО: исключите из своих математических выкладок все величины, полученные на основе классической механики.

В процитированном выше отрывке А.К. Тимерязев упоминает о формуле Гербера, опубликованная в немецком журнале еще 1898 году (ее перевод на русском языке можно найти в Интернете [11]), и которая странным образом совпала с формулой Эйнштейна. Можно ли доверять выводу формулы, сделанному Гербером? Релятивисты хором отвечают — нет. Но и сторонники классической науки относятся к его доказательству скептически. В книге Роузвера дается подробное разъяснение, которое начинается с предварительного замечания:

«Но физики обсуждали и конечные скорости распространения гравитационных взаимодействий; это нашло естественное отражение в законах тяготения с зависимостью от скорости, среди которых наиболее известен закон Вебера. Законами такого типа можно было объяснить и смещение перигелия Меркурия, хотя требуемые для полного объяснения смещения скорости передачи взаимодействий меньше скорости света. Из всех законов подобного рода только закон Гербера дает полное значение смещения при скорости, равной скорости света, однако большинство физиков считали его несостоятельным» [5, 4.4].

Цель, которую перед собой ставил Пауль Гербер в статье 1898 года, состояла в том, чтобы доказать: гравитация распространяется со скоростью света. Поскольку в окончательное выражение вошла скорость света, он констатировал, что она и есть скорость распространения гравитации. Однако по характеру вывода окончательной формулы можно определенно сказать: Гербер знал ее заранее. Разложение исходного выражения в ряд, пренебрежение малыми членами и наличие членов, содержащих дробные показатели степени вида 5/2 и 3/2, лишают его математические выкладки всякого физического смысла. Кроме того, представленное автором доказательство из первых принципов слишком громоздко и запутано, чтобы его можно было проверить на математическую корректность. Читателю приходиться поверить автору на слова, что из предположения о равенстве скоростей распространения электромагнитных и гравитационных возбуждений вытекает формула для векового сдвига перигелия Меркурия. Почему скорость света входит в эту одну-единственную формулу и не фигурирует в других формулах небесной механики, остается загадкой.

– IV –

В русскоязычной литературе нет непредвзятых исторических исследований, посвященных возникновению и обоснованию формулы Гербера – Эйнштейна. Автор книги «Перигелий Меркурия: от Леверье до Эйнштейна» тоже не стоял на безупречно объективных позициях. По нижеприведенным фрагментам чувствуется, что его симпатии больше на стороне релятивистов, чем антирелятивистов.

Да, Гербер ошибался, но ведь и Эйнштейн пришел к его формуле спекулятивным путем. Не вызывает никаких сомнений, что перед взором создателя общей теории относительности уже стояло готовое математическое выражение Гербера, дающее заветное число в 43 угловых секунды за столетие. Чтобы дать почувствовать нашему читателю всю сложность и запутанность проблемы, связанной с формулой Гербера – Эйнштейна, приведем обширную выдержку из шестой главы исторических исследований Роузвера.

«В течение первых двух десятилетий нашего века теория Ритца и общая теория относительности имели конкурента. Это была гипотеза, которая не претендовала на всеобъемлющее объяснение гравитации и электродинамики, но давала простую формулу гравитационных сил, позволяющую без введения произвольных постоянных и исключения каких-либо членов полностью объяснить смещение перигелия Меркурия. Такая формула была предложена Паулем Гербером.

Гербер был преподавателем реальной гимназии в Штаргарде (Померания). Он родился в Берлине в 1854 г., точная дата его смерти, приходящаяся на период 1902 – 1917 гг., остается неизвестной. Герберу принадлежат лишь несколько научных работ, однако им было написано немало статей для научно-популярных журналов. Предложенная им формула силы взаимодействия была опубликована в 1898 г. [132], а более подробное изложение представлено в статье 1902 г. [133]. В 1917 г. по настоянию Эрнста Герке эта статья была напечатана повторно [134]. Значение работы Гербера состояло не только в том, что она предсказывала верное значение аномального смещения перигелия Меркурия. Помимо того, она использовалась как оружие против теории относительности в развернувшейся в то время в Германии кампании нападок на Эйнштейна, в которой Герке играл ведущую роль. Сам Гербер считал себя продолжателем традиций уже упоминавшихся нами ученых, и в его статье, написанной в 1902 г., содержался обзор большинства работ, рассмотренных нами ранее. Вывод его формулы довольно запутанный, но приведенные ниже выкладки дают требуемый результат.

Предложенный Гербером закон взаимодействия обладает замечательным свойством: если положить v равной скорости света, то предсказываемое им смещение перигелия Меркурия составит 41". Для Венеры соответствующее значение равно 8", как следует из закона Ритца и общей теории относительности, а значения для других планет и лунного перигея достаточно малы, чтобы согласоваться с наблюдениями. Казалось, что эта формула устранила препятствие, не позволяющее принять выражения, подобные закону Вебера, в теории тяготения. Она полностью объясняла аномальное смещение перигелия Меркурия при выборе скорости света в качестве "естественной" скорости распространения. После первой публикации формула Гербера не привлекала особого внимания, хотя она и появлялась в некоторых книгах [234, с. 201; 236, с. 235; 396; 87]. Она никак не упоминалась в лекциях Пуанкаре 1906-1907 гг., посвященных пределам применимости закона Ньютона [287]. Интерес к ней был возрожден Эрнстом Герке с появлением общей теории относительности Эйнштейна. Из формулы Гербера следует выражение для смещения перигелия Меркурия … в точности соответствующее полученному в теории относительности. Герке отметил этот факт в статье [129], содержащей критику теории Эйнштейна, утверждая, что приоритет принадлежит Герберу.

Нужно сказать, что Герке был довольно важной фигурой, поскольку являлся одним из ведущих членов "Общества немецких естествоиспытателей", учрежденного с целью дискредитировать Эйнштейна и его теорию относительности. Эйнштейн окрестил это общество, выступавшее на уровне популярной литературы, "антирелятивистской компанией". Возглавлял его Пауль Вейланд, о котором Рональд Кларк писал как о человеке, совершенно неизвестном в научных кругах и в течение многих лет ничем себя не проявившем [61, с. 256 – 259]. Определенный научный престиж этому обществу придавало членство Филиппа Ленарда, которому была присуждена Нобелевская премия за работы в области экспериментальной физики и который позже написал книгу [212] антисемитской ориентации. Однако аргументы, приведенные Герке, показывают, что в деятельности этого разнородного объединения все же присутствовала некая научная основа.

В то время еще не были известны соответствующие данные наблюдений солнечных затмений, а красное смещение в спектре Солнца оставалось под вопросом, поэтому казалось, что эмпирическое подтверждение теории относительности целиком связано с эффектом аномального смещения перигелия Меркурия. И вот оказалось, что существует гораздо более простая теория, которая предсказывает такой же результат в отношении этой важнейшей аномалии, как и теория относительности. Благодаря усилиям Герке статья Гербера [133] в 1917 г. была повторно опубликована в журнале "Annalen der Physik", и на этот раз ее публикация нашла отклик.

Первым свои критические замечания высказал Зеелигер [330], автор гипотезы, объяснявшей смещение перигелия Меркурия влиянием вещества зодиакального света (см. гл. 4). Он утверждал, что расчеты Гербера основаны на элементарной ошибке, хотя теперь очевидно, что ошибся сам Зеелигер. Он также возражал против введения потенциалов, зависящих от скорости, но не в этом суть. …

Зеелигер повторил свои замечания и позже, в 1917 г. [331], когда он допустил возможность использования потенциала, который Карл Нейман назвал эффективным. Однако Гербер имел в виду совсем иное, хотя, возможно, он и сам не вполне понимал смысл введенного им потенциала, представляя лишь, что этот потенциал зависит от скорости, причем скорость его распространения равна скорости света. В конце своей статьи Зеелигер процитировал замечание Неймана [253] по поводу того, что распространение эффективного потенциала представляет собой "совершенно трансцендентальное понятие, существенно отличающееся от распространения света или тепла" [см. 274, с. 186].

Однако, как показывает содержание предыдущего абзаца работы Неймана, эта трансцендентальность связана не с характером распространения, а с природой самого взаимодействия [см. 274, с. 186]: "Мы рассматриваем этот потенциал как стимул к движению или, если использовать более подходящее выражение, как команду, которая подается и излучается в одной точке, а принимается и исполняется в другой; мы предполагаем, что для прохождения этой команды от места передачи до места приема требуется определенное время".

Получение потенциала составляет существенную часть теории Гербера, поскольку его формула (6.24) выведена при рассмотрении влияния, которое конечное время распространения оказывает, во-первых, на расстояние и, во-вторых, на количество полученного потенциала. Во втором случае возможна интерпретация в рамках представлений Ритца о гипотетических частицах: чем быстрее поглощающее тело движется по направлению к излучающему, тем больше частиц "собирает" оно, и аналогично, чем быстрее движется излучающее тело, тем быстрее движутся излучаемые им частицы и тем больше их поглощается в единицу времени. Однако детали этого процесса представить трудно.

В 1918 г. Герке опубликовал статью, в которой поддерживал концепцию эфира и высказывал критические замечания по адресу Зеелигера [130]. После ответа со стороны Эйнштейна [107] (по поводу эфира) и Зеелигера [332] Герке выступил с новой статьей [131]. Он утверждал, что возражения против теории Гербера необъективны и вызваны приверженностью Зеелигера собственному объяснению аномалии.

Появились и другие отклики на повторно опубликованную статью Гербера. Оппенгейм, написавший в 1895 г. обзор гравитационных теорий, опирающихся на конечную скорость распространения, напечатал выдержку из своей статьи, посвященной ньютонову закону всемирного тяготения [271]. Он [написал:] "Я воздерживаюсь от решения по вопросу о том, насколько проведенное им [Гербером] доказательство правильно и удовлетворительно с точки зрения физиков".

По поводу статьи Гербера выступил также фон Лауэ [205], высказавший свое нежелание принять объединенную концепцию дальнодействия и распространяющегося действия.

Далеко не все физики предпочли воздержаться, как Оппенгейм. Фон Гляйх [135] отметил, что теория Гербера предсказывает такое же смещение перигелия Меркурия, как и теория относительности Эйнштейна, но добавил: "Однако обоснование его потенциала нельзя считать верным" [135, с. 230]. Фон Лауэ также писал по этому поводу: "То, что Гербер преподносит как физические соображения, кажется невразумительным... Поэтому мы не можем считать работу Гербера физическим объяснением эффекта" [207, с. 736].

Фон Лауэ пришел к выводу, что в своей работе Гербер исходил из конечного результата, следуя пути, указанному Оппенгеймом. Бухерер также высказал свое отношение к теории Гербера [44, с. 5]: "Заслуга Гербера состоит в попытке рассчитать орбиту Меркурия, исходя из предположения о распространении гравитационного действия со скоростью света. Он вывел — разумеется, при помощи ошибочных заключений — формулу, предсказывающую такое же смещение перигелия, как и формула Эйнштейна".

Итак, неясная по своему характеру работа Гербера породила соответственно туманные отклики. Однако дискуссии можно было бы избежать, указав, что закон силы Гербера фактически опровергался по двум причинам.

Как было показано, этот закон приводил к такому же выражению для смещения перигелия, как и общая теория относительности. Однако теория Гербера была применима лишь к гравитации и вне этой области ни о чем не говорила. Поэтому для создания полной физической картины ее требовалось дополнить, в частности, теорией электродинамики. Во время появления общей теории относительности это могла быть либо теория Лоренца, либо специальная теория относительности, но, как мы увидим в следующей главе, обе эти теории приводили к одной и той же зависимости массы от скорости. Эта зависимость, учитываемая в рамках "ньютонианской" теории, приводила к значению 1" в столетие для смещения перигелия Меркурия *). [Сноска *) Разумеется, ньютонова теория несовместима со специальной теорией относительности, поскольку в отличие от последней в ней предполагается бесконечная скорость распространения гравитационного действия. Теория Гербера в этом отношении совместима со специальной теорией относительности.]

Как уже отмечалось в гл. 4, де Ситтер в 1913 г. показал, что это значение вполне укладывалось в рамки общепринятого тогда объяснения аномалии на основе ньютоновой теории, если исходить из гипотезы Зеелигера о зодиакальном свете и слегка уменьшить плотность пылевого вещества. Это релятивистское движение перигелия необходимо учитывать и в приложении к теории тяготения. В общей теории относительности это подразумевается, так как она включает в себя специальную теорию относительности.

Это молчаливо предполагалось и в незаконченной теории Ритца 1909 г., поскольку последняя должна была охватывать как электродинамику, так и гравитацию и предусматривать изменение массы и другие следствия электродинамической теории Ритца [274, с. 620]. При использовании в 1908 г. формулы Ритца в качестве чисто гравитационного закона следовало бы добавить смещение за счет электродинамического эффекта, но поскольку соответствие вычисленной величины аномалии наблюдениям устанавливалось путем принятия специальных предположений, это обстоятельство не опровергало закона Ритца.

Однако кажущееся преимущество формулы Гербера, не требующей подгонки постоянных, в данном случае обратилось против нее, так как и здесь требуется добавить релятивистский эффект, что в совокупности приводит к смещению перигелия Меркурия, равному 49" в столетие. В то время как небольшая заниженность расчетного значения по сравнению с наблюдаемым может быть приписана малому сжатию Солнца или наличию пылевого вещества внутри орбиты Меркурия, даже небольшой избыток объяснить очень трудно. Никто не отваживался утверждать, что Солнце на самом деле вытянуто вдоль оси вращения, а значение смещения, равное 42" в столетие, если и оспаривалось, то поправки вносились в сторону его уменьшения. Таким образом, закон Гербера не обеспечивал верного предвычисления смещения перигелия.

Вторая причина, по которой закон Гербера следовало бы отвергнуть, — это эффект отклонения световых лучей в гравитационном поле Солнца. Правда, в то время его существование подвергалось сомнению. Ранее уже обсуждалось отклонение света в гравитационном поле Солнца в соответствии с теорией Ритца. Мы считали световой луч состоящим из частиц, проходящих вблизи массивного тела. Аналогичный подход можно повторить и при исследовании закона Гербера. ...

Приведенные соображения следует рассматривать как явное опровержение закона Гербера. Ранние результаты наблюдений солнечных затмений не принесли окончательного подтверждения общей теории относительности [195]. Экспедиция в Собраль 1919 г. получила значение 1,98" +0,16', свидетельствующее в пользу этой теории в том смысле, что соперничающие теории Нордстрема и "ньютонианская" предсказали соответственно полное отсутствие эффекта и отклонение, равное 0,87". Полученные данные также подтверждали превосходство общей теории относительности над теориями Ритца и Гербера, которые предсказывали значения 1,31" и 2,62" соответственно. Однако более поздние измерения привели к результатам, которые превышают значение, предсказываемое теорией Эйнштейна. Из них следует отметить результат измерений Фрейндлиха в 1929 г. (2,24" + 0,10"), промежуточный между значениями, вытекающими из теорий Эйнштейна и Гербера. Результат 2,73" + 0,31", полученный в СССР в 1949 г., позволяет отдать предпочтение теории Гербера, однако более поздние измерения не подтвердили столь значительное отклонение, и опровержение общей теории относительности не состоялось. Данные наблюдений солнечных затмений, полученные в период между экспедицией в Собраль и измерениями Фрейндлиха, говорили в пользу общей теории относительности Эйнштейна. Поскольку сторонники Эйнштейна не обращали внимания на теорию Гербера, а защитники этой теории не были склонны заявлять о своем поражении, неудивительно, что в этот период ссылки в литературе на результат Гербера отсутствуют. Однако возможно, что в 1929 г. какие-то замечания о теории Гербера появлялись в печати. Так или иначе, закон Гербера канул в небытие, хотя и не был публично опровергнут» [5, гл. 6].

– V –

Роузвер и другие авторы не исключают, что формулу Гербера – Эйнштейна можно было получить эмпирическим путем из общих соображений и небольшой подгонки. В самом деле, для этого нужно было всего-навсего знать элементарные законы небесной механики, которые опираются на полярное уравнение конического сечния:

ρ = p / ( 1 – e cos φ ).

где e — эксцентриситет конического сечения, p — параметр. Для эллиптической орбиты параметр равен:

p = a ( 1 – e² ).

где a — большая полуось эллипса.

В разделе, рассказывающем об Отклонении лучей света вблизи массивных тел (подраздел III), мы получили угол пертурбации при условии:

с² / p = с² / a ( 1 – e² ) = g = GMr ^–2 ,

где c — скорость света, G — гравитационная постоянная, M — масса Солнца, r = AF — перигелий Меркурия и g — ускорение свободного падения в точке перигелия (A).

Формулу, которую получил Зольднер (*) и Захаров (10) из предыдущего раздела, сводилась к виду:

Θ = α = ω = 2GM / pс² = 2GM / a( 1 – e² )с².

По всей видимости, Гербер взял за основу последнее выражение и записал его в виде:

,     ( А )

где Δφ известная из астрономических наблюдений величина, k — подгоночный коэффициент, который очень удобно умножается на полный оборот в 2π, так как речь идет о долях углового поворота, т.е. о прирощении за один оборот Меркурия вокруг Солнца.

Первая планета имеет большую полуось орбиты, равную a = 57,91 · 10 ¹¹ см, эксцентриситет e = 0,2056, период обращения T = 0,241 года или 87,969 суток (см. данные по Меркурию), т.е. за сто лет он совершает 415 оборотов. Пусть перигелий Меркурия за сто лет сдвигается на 43", как рассчитал Эйнштейн. Тогда за один оборот (φ = 2π) перигелий дополнительно повернется на угол Δφ = 0",1036 ≈ 0,502 · 10 ^–6 радиан. Подставляя это значение Δφ, а также числовые значения скорости света c = 2,997 · 10 ¹⁰ см/с, гравитационной постоянной G = 6,673 · 10 ^–8 дин · см²/г² и массы Солнца M = 1,989 · 10 ³³ г в последнее выражение, находим, что искомый коэффициент равен k = 3 (точнее: 3,000138). Учитывая третий закон Кеплера,

GM = 4π²a³/T²,

формулу Гербера (А) можно представить как

.     ( Б )

В работе 1915 года «Объяснение перигелия Меркурия» после разложения в ряд и удержания двух первых членов Эйнштейн написал: «… при целом обороте перигелий перемещается на угол

,     ( А' )

если через a обозначить большую полуось, а через e — эксцентриситет орбиты.

Если мы введем период оборота T (в сек), то получим, обозначив через c скорость света (в см/сек),

.     ( Б' )

Вычисление дает для планеты Меркурий поворот перигелия на 43" в столетие, тогда как астрономы указывают 45" ± 5" в качестве необъяснимой разницы между наблюдениями и теорией Ньютона. Это означает полное согласие с наблюдениями» [13, т. 1, с. 446 – 447].

Заметим, во-первых: в приведенной здесь формуле ( А' ) под α понимается константа, которой Эйнштейн часто пользовался: 2GM / с². Таким образом, эйнштейновская формула ( А' ) в действительности есть герберовская формула ( А ). Во-вторых, в формуле ( Б' ) советского издания «Собрания научных трудов Эйнштейна» сделана описка, а именно, пропущена цифра «4». Ниже приведена эта же формула, но взята она уже из немецкого оригинала:

    ( Б' )

Таким образом, эйнштейновская формула ( Б' ) также в точности совпадает с герберовской формуле ( Б ).

Итак, окончательные выражения у Гербера и Эйнштейна тождественны. Они возникли как модификация формулы Зольднера 1801 года, которую еще раньше, в 1784 году, вывел Генри Кавендиш. В общем, как мы видели на примере выкладок А.М. Петрова, формула (*) получается элементарно из общего уравнения для конических сечений. Можно предположить, что Гербер знал о выводе Зольднера или получил его выражение самостоятельно, как сделал это до него Кавендиш. Далее он подогнал коэффициент k, природа которого оказалась удивительной. Ведь для его получения используются либо очень маленькие, либо очень большие астрономические и физические константы, тем не менее, в результате получается небольшое целое число, равное 3, причем с высочайшей точностью. Такая степень точности сразу делает выкладк Гербера и Эйнштейна подозрительными, поскольку те использовали приближенные вычисления.

Возможно, этот факт объясняется наличием в динамике планет синхронизмов или, как их еще называют, резонансов. Вспомним, период осевого вращения Меркурия равен 58,6462 суткам, что составляет τ = 0,161 в единицах земного года. Его период обращения вокруг Солнца, как было сказано, равен T = 0,241; в отношении T / τ = 3/2 входит число 3. По существу, в формулах (А) и (А') стоит не полный оборот 2π, а только полуоборот π, так как множитель 2 является неотъемлемой частью формулы Зольднера или эйнштейновской постоянной α. Поэтому в этих формулах нужно вводить еще один множитель 2. Тогда подгоночный коэффициент будет равен уже 3/2. Кстати, точно такая же пропорция выполняется для Венеры. Пифагор был, видимо, прав: миром правит гармония целых чисел (более подробно об этом читайте в разделе Дискретная гравитация и аттракторы ).

На вопрос, почему k = 3/2, можно будет ответить так: потому что отношение периода обращения Меркурия вокруг Солнца к периоду его обращения вокруг оси равно пропорции 3 : 2. Если затем возникает следующий вопрос: почему у Меркурия T / τ = 3/2? На него мы задаем встречный вопрос: а почему, собственно, период обращения Луны вокруг Земли к периоду обращения ее вокруг оси равно отношению 1 : 1? Ясно ведь, что механика синхронизмов развита еще плохо и подобные резонансы прогнозировать сложно. Мы из наблюдений знаем, что Луна испытывает либрацию, т.е. слегка колеблется возле равновесного состояния, которое выражено пропорцией T / τ = 1/1. Следовательно, здесь действует механика аттрактора, но как рассчитывать частоту и амплитуду автоколебаний, величину возвратной силы и т.д., мы еще не достаточно хорошо представляем.

Самой большой загадкой, является, конечно, участие в этих формулах константы скорости света. Мы с подозрением относимся к результатам Эксперимента Фомалонта – Копейкина : авторы не убедили нас, что скорость распространения гравитации равна скорости света. Более того, нам не известна механика действия гравитации. В нынешней картине мира классической физики электромагнитное излучение не должно взаимодействовать с гравитационным полем, т.е. гравитационная постоянная и постоянная скорости света не могут входить в одно уравнение. Но возможно, притяжение Луны к Земле, Земли к Солнцу и т.д. происходит не по кратчайшим прямым, соединяющим космические тела, а само понятие «притяжение» иллюзорно. Солнечная система формируется по линии согласования вращающихся моментов всех входящих в нее космических тел, а всемирный закон тяготения и законы Кеплера являются только следствием длительного процесса согласования (такая точка зрения высказывается в разделе Вихри в твердом космосе). Может быть, в этой картине мира появятся уравнения, в которых гравитационная постоянная и постоянная скорости света будут участвовать на равных правах. Но пока формула Гербера, наряду с формулой Зольднера, выглядят как-то неестественно.

Если иметь в виду классическое объяснение, то сегодня обнаружены новые факторы ньютоновского свойства, способные влиять на аномальное движение первой планеты. Например, «В те далекие времена, — пишет Геннадий Ивченков, — считали, что центр вращения Солнца и всей солнечной системы совпадает с геометрическим центром Солнца, что, оказалось, не соответствует действительности» [12]. В самом деле, на рис. 76 в разделе Фракталы и солнечная система показано перемещение центра тяжести солнечной системы относительно геометрического центра Солнца в период с 1945 по 1994 год. Что-то не было слышно, чтобы Клеменс или кто-либо другой учитывали это явление.

Таким образом, формула Гербера – Эйнштейна была и остается загадкой — ни классические объяснения Гербера, ни релятивистские объяснения Эйнштейна для неё не годятся. Как только Гербер нашел коэффициент k, у него появилось желание найти какое-то объяснение для фигурирующей в нём скорости света. Он предположил, что гравитация, очевидно, распространяется со скоростью электромагнитных волн. Сначала на это «высосанное из пальца» объяснение никто особо не обратил внимание. Но потом появилась ОТО; внутри этой искусственной теории Эйнштейна — более искусственной, чем теория Гербера, — эмпирически подогнанная формула зазвучала с невероятной силой. Теперь она сделалась жупелом как для сторонников, так и противников релятивистской физики. Всё, что требовалось от Эйнштейна, это подвести некую теоретическую базу для оправдания целочисленного коэффициента k = 3. Сделал он это не удовлетворительным образом, опираясь на философию Маха. А.К. Тимерязев детально разбирает его методические и логические ошибки в работе [9] (она есть у нас на сайте, см. Теория относительности Эйнштейна и махизм).

– VI –

Однако «в те далекие времена» аномальное смещение перигелия Меркурия в принципе приемлемым образом, без всяких экзотических предположений, вроде искривления пространства, было объяснено немецким астрономом, директором Мюнхенской обсерватории, Хуго Зеелигером (1849 — 1924), который в 1906 г. предложил для этого так называемую материальную теорию, которая в ходе релятивистской революции вместе с другими конструктивными теориями была просто отброшена, как не отвечающая духу времени. Как писал Роузвер, теория Зеелигера «завоевала широкую поддержку, объясняла всё, что требовалось, и вдобавок не противоречила наблюдаемым фактам» [5, с. 85]. При этом ее автор исходил из вполне очевидных фактов: наличия в околосолнечном пространстве огромного количества выбрасываемого Солнцем вещества, которое и могло привести к аномалии в движении первой от Солнца планеты.

Что можно наблюдать с помощью современной аппаратуры в непосредственной близи и на некотором удалении от Солнца? В периоды его активности корона достигает 50 солнечных радиусов, а орбита Меркурия проходит в районе 80 солнечных радиусов. Не только Меркурий, но все четыре малых планеты находятся, можно сказать, в верхних слоях атмосферы Солнца, от жесткого излучения которого нас спасает магнитное поле Земли и многокилометровый воздушный флюс. Средняя плотность солнечного вещества всего в 1,4 раза больше воды. Однако в центре Солнца давление неизмеримо выше, чем на его поверхности, так что границу его шаровой поверхности можно выделить весьма условно. На сотни тысяч километров простирается плазменная среда. Высоченные фонтаны постоянно вырываются из недр Солнца, причем их мощные всплески весьма неравномерны как в пространственном, так и во временном отношении. Между тем, всякая неравномерность в плотности вещества, находящегося в околосолнечном пространстве, создает дополнительные моменты для сдвига перигелия Меркурия и других планет.

Солнечный ветер, состоящий из электронов, протонов, ионов водорода и гелия, создает вблизи Меркурия материальную среду, далекую от вакуума. Скорость ветра меняется в пределах от 300 до 750 км/с, а плотность вещества достигает 10² ÷ 10⁴ протонов на см³ (многое зависит от активности светила). Кроме того, имеется межпланетная среда — крохотные микрочастицы размерами от 25 до 100 мкм. На Землю ежегодно выпадает примерно миллион тонн подобной пыли. При прохождении Солнца вблизи Крабовидной туманности и других мощных источников радиоизлучения можно просвечивать структуру сгустков межпланетной среды и изучать плотность солнечного ветра. Открыт солнечный ветер в 1959 году советским КА «Луна-2».

Но уже во времена Зеелигера о распределении вещества вблизи Солнца можно было судить по зодиакальному свечению, которое видно даже невооруженным глазом в форме слабой светлой полосы, вытянутой под небольшим углом к эклиптике. Объясняется это свечение рассеиванием частиц солнечного ветра на частицах межпланетной пыли. Замечено также, что чем ближе к Солнцу, тем ярче зодиакальный свет, что свидетельствует о повышенной плотности в том месте. Экваториальная плоскость светила, в которой происходит максимальный выброс вещества, наклонена примерно под углом 7° к плоскости эклиптики. Если бы эти две плоскости совпадали, то аномальный сдвиг перигелия был бы гораздо меньше, поскольку на «неправильность» движения планеты сказывается прежде всего неоднородность распыленной массы.

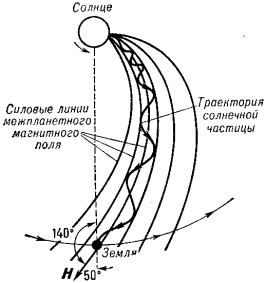
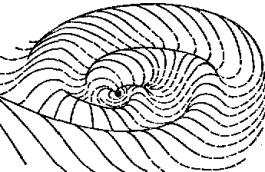
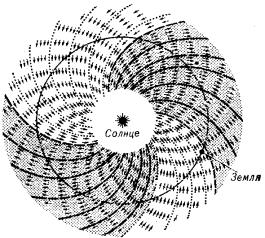
Рис. 3. На распределение ионизированного газа в межпланетном пространстве в большей степени влияет не гравитационное, а магнитное поле. На верхнем чертеже показана винтовая траектория движения протона. Силовые линии магнитного поля Солнца вытягиваются солнечным ветром и закручиваются 27-суточным периодом вращения светила в архимедову спираль. В результате этого движения межпланетный токовый слой приобретает гофрированную поверхность, как это показано на среднем чертеже. Американский аппарат IMP-1 зарегистрировал секторную структуру межпланетного магнитного поля. На нижнем рисунке в темных секторах мы видим силовые линии, направленные от Солнца, в светлых секторах — к Солнцу.

На рис. 3 показано действие магнитного поля в межпланетном пространстве. На поток плазмы, вырывавшейся из недр светила, в первую очередь действуют магнитное поле Солнца, которое оказывается как бы вмороженным в межпланетное пространство, так как оно сохраняется в токах заряженных частиц. Движение этих частиц в магнитном поле можно представить как суперпозицию двух движений: прямолинейного вдоль магнитных силовых линий и вращательного в плоскости, перпендикулярной этим линиям. В результате их движение получается винтовым. С помощью спутниковой аппаратуры удалось измерить вблизи Земли мощный поток протонов, образующих солнечный ветер; поток оказался равным примерно 10 ⁷ — 10 ⁹ протонов/см² · с. Из-за вращения Солнца токовые плотности протонов образуют пространственную функцию в виде раскручивающиеся спирали гофрированной поверхности. Сечение этой неровной поверхности плоскостью эклиптики дает секторную структуру межпланетного магнитного поля.

Таким образом, Меркурий, Земля и прочие планеты Солнечной системы вращаются отнюдь не в вакууме, а в очень плотной, существенно неоднородной и динамически развивающейся среде, которая не может не влиять на вековые движения близких к Солнцу планет. Миллиарды тонн вещества распылены в межпланетном пространстве, которые воздействуют на распределение гравитационного потенциала. Следует также иметь в виду, что одна секунда дуги — это угол, под которым видна копеечная монетка с расстояния три километра. И когда говорится, что четыре десятка секунд набегает за столетие, то эта весьма скромная аномалия скорее всего вызвана влиянием межпланетного вещества. Релятивисты, игнорирующие данный материальный фактор, допускает серьезный просчет. Их математические вычисления бывают весьма сложными, но они не имеют никакого отношения к действительному положению вещей. Если берется только холодная масса Солнца вместе со своими девятью планетами и помещается в абсолютно пустое пространство, и при этом получается 43 секунды, то немедленно возникает вопрос: что делать с той колоссальной массой вещества, которая регистрируется космическими аппаратами?

Зеелигер не имел информации о динамическом плотности солнечного ветра и межпланетной среды, которая постоянно меняется в зависимости от вспышек на Солнце. Поэтому он ввел несколько усредненных эллипсоидов материальной среды, два из которых с полуосями, равными 0,24 и 1,20 а.е., по его мнению, максимально влияли на движение первых четырех планет. Так как полуось орбиты Меркурия равна 0,39 а.е., а Земли — 1,0 а.е., то первый эллипсоид расположился внутри орбиты Меркурия, а второй — за пределами орбиты Земли (он бы вообще не понадобился, если бы не учитывалась аномалия Марса).

Итак, при желании извержениями солнечного вещества можно объяснять и отклонение лучей от звезд вблизи солнечного диска и аномальное отклонение перигелия Меркурия. Однако сегодня сложилась такая ситуация, когда ни сторонники, ни противники релятивисткой догмы не могут пользоваться этими двумя фактами в качестве безупречного доказательства, так как оба лагеря лишены достоверной научной информации. Собственно, споры возникли не сегодня, а в самом начале обсуждения релятивистской теории. Чтобы передать атмосферу дискуссий тех далеких дней, приведем из седьмой главы книги Роузвера характерный фрагмент.

«Однако смещение перигелия представляет собой более сложный эффект, нежели гравитационное красное смещение и отклонение световых лучей. Для начала можно хотя бы указать, что он относится к реальным планетам, которые не являются материальными точками. Если новая теория полностью объясняет смещение перигелия, она должна приводить к таким же результатам в отношении возмущений, как ньютонова небесная механика. Этот аспект был затронут Максом Борном в дискуссии, последовавшей за лекцией, прочитанной Эйнштейном в 1913 г. в Вене [101].

Борн: "Я должен задать вопрос г-ну Эйнштейну: а именно, как быстро распространяется гравитационное действие в вашей теории? Для меня далеко не очевидно, что распространение происходит со скоростью света, связь должна быть очень сложной".

Эйнштейн: "Уравнения для случая, когда возмущения, которым подвергается поле, бесконечно малы, записать нетрудно. Тогда значения g отличаются от невозмущенных лишь на бесконечно малую величину; возмущения распространяются тогда с такой же скоростью, как свет".

Борн: "Но вопрос действительно осложняется при больших возмущениях?"

Эйнштейн: "Да, тогда проблема становится математически сложной. В общем случае трудно найти точные решения уравнений, поскольку они нелинейны".

Макс Лауэ в качестве одной из причин, помешавших принять ему безоговорочно общую теорию относительности, отметил свое убеждение, что расчеты смещения перигелия неприменимы к протяженным телам. Как показал недавно Дафф [94], даже вопрос о том, является смещение перигелия в общей теории относительности эффектом первого или же второго порядка, нуждается в обсуждении. Соображения такого рода позволяли предположить, что простые вычисления смещения перигелия могут оказаться несостоятельными, будучи примененными к реальным небесным телам. Возможно, Эйнштейн предусмотрел такую возможность, когда опубликовал подобные расчеты для красного смещения и отклонения световых лучей в гравитационном поле, но не для смещения перигелия. Теперь мы знаем, что в действительности трудностей не возникало и из метрики можно вывести выражения для всех трех рассмотренных эффектов. Однако при создании новой теории у Эйнштейна, разумеется, было гораздо меньше оснований для такой уверенности» [5, гл. 7].

Антирелятивисты данный оптимизм Роузвера по понятным причинам не разделяют. Общей релятивистской теории, собственно, не существует; есть спекулятивные рассуждения и некорректные математические манипуляции вокруг трех астрономических фактов. Брать их сегодня за доказательство истинности ОТО — значит пожертвовать своей научной репутацией в обмен на лояльность к академическим институтам науки, вызывающим у истинного исследователя чувство брезгливости.

Глава VII «Экспериментальные основания общей теории относительности» сборника статьей «Альберт Эйнштейн и теория гравитации» [8], выпущенного к 100-летию отца-основателя теории относительности, начинается с трех экспериментов, подтверждающих принцип эквивалентности инертной и гравитационной массы (раздел А). Поскольку эта эквивалентность не противоречит классической механике, ее нельзя принимать в качестве аргумента в пользу исключительной истинности ОТО.

В разделе Б главы VII указанного сборника — «Смещение перигелия Меркурия» — упоминаются «Радиолокационные измерения движения перигелия Меркурия» [Shapiro I. I., Pettengill G. H., Ash M. E., Ingalls R. P., Campbell D. В., Dyce R. Б., Physical Review Letters, 28, 1594 (1972)]. В аннотации сказано: «Измерения задержки радиолокационных сигналов, посланных от Земли к Меркурию и отраженных обратно, дали правильное значение смещения точки перигелия этой планеты». Установление точного значения смещения перигелия еще не подтверждает справедливость ОТО. Главной проблемой здесь является сама постановка задачи. Основным экспериментом, на котором держится ОТО, был и остается эксперимент, проведенный под руководством Эддингтона в 1919 году (о нём подробно рассказывалось в предыдущем разделе, в V и VI его частях).

---

1. Рябов Ю.А. Движение небесных тел. — М., Наука, 1988.
2. Белецкий В.В. Движение спутника относительно центра масс в гравитационном поле. — М.: МГУ, 1975.
3. Белецкий В.В., Хентов А.А. Резонансные вращения небесных тел. — Нижний Новгород, 1995.
4. Брумберг В.А. Релятивистская небесная механика. — М.: Наука, 1972.
5. Роузвер Н.Т. Перигелий Меркурия: от Леверье до Эйнштейна. — М.: Мир, 1985.
6. Тимирязев А.К. Теория относительности Эйнштейна и диалектический материализм / «Под Знаменем Марксизма» 1924 г., № 8–9, с. 142 – 157; № 10–11, с. 93 — 114.
7. Тимирязев А.К. Введение в теоретическую физику. — М.- Л.: ГТТИ, 1933.
8. Альберт Эйнштейн и теория гравитации / Сборник статей. — М.: Мир, 1979.
9. Тимирязев А.К. Теория относительности Эйнштейна и махизм / Стенограмма доклада на заседании Комм. Акад. — 7/II 1924 г. // Опубликована в сборнике статей «Естествознание и диалектический материализм». — М.: Материалист, 1925, с. 228–258.
10. Бронштэн В.А. Как движется Луна? — М.: Наука, 1990.
11. Гербер, Пауль. Пространственное и временное распространение гравитации (перевод на русский Йохана Керна (Johann Kern) , 2004 ( http://bourabai.kz/articles/gerber/gerber-rus.htm ).
12. Ивченков, Геннадий. Самое важное подтверждение ОТО, или что измерил лорд Эддингтон ( http://bourabai.kz/articles/ivchenkov.htm ).
13. Эйнштейн А. Собрание научных трудов в 4-х томах. / Под ред. И.Е. Тамма, Я.А. Смородинского и Б.Г. Кузнецова. — М.: Наука, 1965.