От Архимеда до Дюрера

О.Е. Акимов

Архимед родился в 287 году до н.э. в сицилийском городе Сиракузы. Его отец, астроном Фидий, с детства привил ему любовь к точным наукам. В молодые годы он учился в Александрии и сохранил дружеские отношения с тамошними учеными, Кононом, Досифеем и Эратосфеном, занимающимися математикой, астрономией и другими естественными науками. Переписываясь с друзьями, он сообщал им свои достижения в области математики, механики и астрономии. Находясь еще в Египте, он изобрел «улитку Архимеда» — бесконечный винт, с помощью которого можно было вычерпывать воду из водоемов. Прибыв в Сиракузы, он вскоре стал служить при дворе сиракузского тирана Гиерона, приходившимся ему дальним родственником. В 215 году Гиерон скончался и на престол вступил его несовершеннолетний внук Гиероним.

Сицилия находилась между молотом (Карфагеном) и наковальней (Римом), столетиями воевавшими между собой за господство над Средиземным морем. В III веке до н.э. Карфаген, основанный финикийцами в 825 году, владел Южной Италией, Сардинией и Сицилией (кроме Сиракуз, остававшимися независимым полисом). Затем Рим, почувствовав силу, повел против него войну. Первая Пуническая война длилась с 264 по 241 год, вторая — 218-201 и третья — 149-146 гг. до н.э. Сиракузы лавировали между двух огней, периодически выступая то на стороне Карфагена, то на стороне Рима. Сразу после смерти Гиерона, в основном поддерживавшего Карфаген, но не ссорившегося с Римом, победу одержала римская партия. Но вскоре она потеряла свое влияние и к власти пришли карфагенская, точнее, греко-карфагенская партия, куда входили и прямые ставленники Ганнибала.

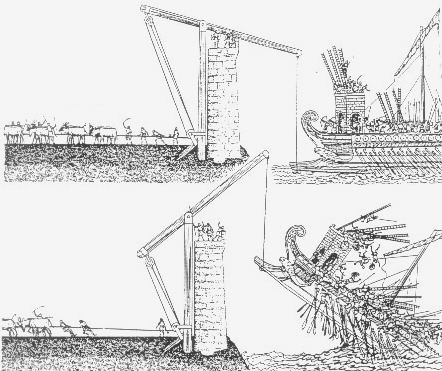
После окончания Первой Пунической войны Гиерон привлек Архимеда для возведения крепостей, оборонительных сооружений и строительства военных машин, к которым относились катапульты, пушки, выбрасывавшие на большое расстояние камни и свинцовые болванки, машины, снабженные подвесными бревнами и журавлиные клювы. Последние захватывали носы вражеских кораблей, приподнимали их и, сотрясая и раскачивая, приводили в негодное состояние. Клювы представляли собою комбинацию блока, винта, зубчатых колес и приводились в действие с помощью волов. Баллистические машины различных размеров передвижные и станковые для метания камней (большая механическая праща) и стрел (большой механический лук) существовали у греков, карфагенян и римлян еще до Архимеда. Ниже в качестве примера приведены рисунки камнемета (palintonon) и стреломет (euthytonon).

С античных времен пришла к нам легенда, повествующая, как Архимед с помощью зеркал поджигал корабли римского флота, штурмовавших в 212 году до н.э. Сиракузы. «Марцелл начал штурм Сиракуз с моря и суши одновременно, обрушив на его стены всю мощь римской армии. Несомненно, это мероприятие оказалось бы более успешным, если бы среди осажденных… в то время не жил один из самых выдающихся ученых древности — Архимед» [1].

Авторитетные историки — Полибий, Тит Ливий и Плутарх, писавшие вскоре после падения города, — о легенде умалчивают, по-видимому, не слишком веря в ее достоверность. Но греческий историк Диодор Сицилийский (1-й век н.э.), сочинения которого не сохранились, в пересказе Цеца об этом писал примерно так: «Когда римские корабли находились на расстоянии полета стрелы, Архимед стал действовать шестиугольным зеркалом, составленным из небольших четырехугольных зеркал, которые можно было двигать при помощи шарниров и металлических планок. Он установил это зеркало так, что... принятые этим зеркалом солнечные лучи, отражаясь, создавали жар, который обращал суда римлян в пепел, хотя они находились на расстоянии полета стрелы...».

После Диодора сатирик Лукиан, живший во 2-м веке н.э. вскользь упомянул, что Архимед «... при помощи своего искусства сжег неприятельские корабли». Примерно в то же самое время известный врач Гален в сочинении «О темпераменте» тоже упомянул, что «Архимед поджег триремы врага зажигательными зеркалами». Но то, что эта легенда является скорее всего былью, подтверждается сочинением «О чудесных механизмах», написанном в 6-м веке н.э. византийским математиком, скульптором и архитектором Анфимием из Тралл. Очевидно, он, пользовался древними источниками, не дошедшими до нас, так как написал: «Следует заметить, что все прочие авторы, которые говорили о зеркалах божественного Архимеда, упоминали не об одном зеркале, но о многих».

Анфимий представил изобретение Архимеда в следующем виде: «...При помощи многих плоских зеркал можно отразить в одну точку такое количество солнечного света, что его объединенное действие вызовет загорание. Этот опыт можно сделать с помощью большого числа людей, каждый из которых будет держать зеркало в нужном положении. Но, чтобы избежать суматохи и путаницы, удобней применить раму, в которой следует закрепить 24 отдельных зеркала с помощью пластин или, еще лучше, на шарнирах. Подставляя этот механизм солнечным лучам, надо правильно установить центральное зеркало, а потом и остальные, быстро и ловко наклоняя их так, чтобы солнечные лучи, отраженные от этих различных зеркал, отражались в ту же точку... Таким образом, если повторять это много раз и ставить другие зеркала, составленные по тому же принципу, что и первое, то все отражения сойдутся и произойдет загорание... Это удастся тем лучше, чем больше будет зеркал».

Столь детальное описание наводит на мысль, что подобную зеркальную установку Анфимий построил собственноручно и проверил в действии. В самом деле, на легенду об Архимеде, существует аналогичная легенда об Анфимии, который методом Архимеда спалил дом соседа после ссоры с ним. В октябре 2005 года студенты Массачусетского технологического института под руководством преподавателей действовали также в отношении условной вражеской флотилии. В центре дуги из зеркал они разместили прицельное зеркало Х; остальные зеркала нацеливали, ориентируясь на него. Такая форма наводки систем из многих зеркал связана с быстрым перемещением Солнца порядка 1,5 метра за 10 минут.

Массачусетским архимедам удалось воспламенить доски макета римской триеры. Аналогичный эксперимент был проведен в 1973 году греческим инженером-экспериментатором Иоаннисом Сакасом (Ioannis Sakas). Шесть-семь десятков моряков медными зеркалами размером 91 × 50 кв. см сожгли деревянное судно груженое смолой, находящееся от них на расстоянии 50 метров.

Аналогичный принцип лежит в современных зеркальных нагревателях, работающих на солнечной энергии, а также в радиотелескопах, наблюдающих за звездным небом в невидимом для глаза диапазоне электромагнитных волн.

Еще раньше, в 1747 году, французский натуралист Жорж Луи Бюффон провел подобный эксперимент после того, как Декарт высказался на сей счет скептически. В шестом мемуаре «Изобретение зеркал для воспламенения предметов на больших расстояниях» он писал: «Декарт, который родился, чтобы судить Архимеда и даже превзойти его высказался против этого случая тоном метра: он отрицал возможность подобного изобретения, и его мнение одержало верх над свидетельствами и верой всей античной эпохи... Чтобы обжаловать приговор Декарта, нужно было располагать более сильным средством, чем просто различные доводы, поэтому противникам Декарта оставалось лишь одно: воспроизвести зеркала Архимеда.

Я задумал эту идею уже давно и охотно признаю, что очень трудно было представить ее осуществленной, поскольку в процессе исполнения я сделал гораздо больше, чем ожидал. … Первый опыт я провел 23 марта 1747 г.: при помощи всего лишь 40 зеркал я воспламенил буковую просмоленную доску на расстоянии 66 футов (22 м), т. е. я использовал только четвертую часть всего составного зеркала. Но здесь следует сказать, что зеркало еще не было установлено, поэтому его положение было очень неудобным, оно образовывало с Солнцем угол наклона около 20°. … 3 апреля в четыре часа дня зеркало было поднято и установлено на свою опору; при помощи 112 зеркал было произведено воспламенение доски, покрытой рубленой шерстью, на расстоянии 138 футов (45 м), хотя солнце было очень слабым.

10 апреля после полудня при достаточно ярком Солнце воспламенили еловую просмоленную доску на расстоянии 150 футов (49 м) всего лишь при помощи 128 зеркал; воспламенение произошло совершенно внезапно, причем на всей площади освещенного пятна. 11 апреля, поскольку фокус находился на расстоянии в 20 футов от зеркала, понадобилось только 12 зеркал, чтобы воспламенить мелкие горючие предметы. При помощи 21 зеркала зажгли буковую доску, с помощью 15 зеркал удалось расплавить большой сосуд олова, весом около 6 фунтов, 117 зеркалами были расплавлены тонкие листы серебра» [1].

Заглянем в историю еще глубже. Дюрер писал: «Если же ты хочешь сделать из вышеназванной параболы, или зажигательной линии, зажигательное зеркало, то сделай высоту до вершины конуса, из которого ты будешь вырезать параболу, не больше ширины его основания, или пусть конус будет иметь форму правильного треугольника. Если ты затем рассечешь его по параболе, и возьмешь эту линию, и сделаешь по ней вогнутое зеркало, и срежешь его немного спереди, то в точке, где соберутся преломившиеся лучи солнца, они будут очень сильно жечь. …

Итак, я провожу поперечную линию ab, под ней понимай плоское зеркало или воду, в которую ты смотришь. Затем с одной стороны наверху я устанавливаю свет c и ставлю напротив, с другой стороны — человечка, который смотрит в зеркало или воду. Если обозначить его глаз d, то глаз увидит свет не раньше, чем углы [наклона] светового луча c, и линии луча зрения d окажутся равными. Это получается следующим образом. Если ты проведешь из точки c, где происходит отражение, отвесную линию вверх и поставишь циркуль одной ножкою в эту точку, другою же ножкою проведешь вверх от линии ab [дугу] и, измерив, найдешь, что луч света c и луч зрения d находятся на одинаковом расстоянии от отвесной линии, то это и будет точка, в которой можно увидеть свет. Если же теперь твое зрение будет направлено через зеркало вниз, то пересечение опущенной из верхнего света c вниз отвесной линии и линии d покажет, на какой глубине будет виднеться свет в воде или в зеркале. Сходным же образом в соответствии со своей природой перекрещиваются лучи солнца в сделанном из линии параболы зеркале, причем все они, выходя из зеркала, собираются в одной точке и сильно жгут, а в чем причина этого, показали математики; кто захочет, может это прочитать. Здесь ты увидишь нарисованным это мое предыдущее объяснение» [3, с. 125-127].

Но еще до Дюрера итальянский художник Леонардо да Винчи рисовал «зажигательные зеркала», которые оказались тесно связанными с геометрией. В подразделе Критика Андрея Радзюкевича приводились два рисунка, свидетельствующих о том, что он проявлял интерес не только к механике, но и к такой чисто математической дисциплине, как геометрия.

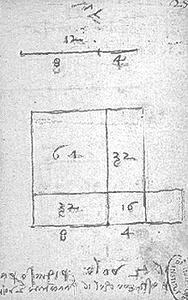
Чертеж слева прост, чертеж справа требует разъяснений; их мы находим в первой книге Альбрехта Дюрера «Руководство к измерению». Ниже приводится чертеж и краткие разъяснения немецкого художника.

Пусть по оси x движется отрезок BD так, чтобы на оси y выполнялось условие: 0C = AB (разъясняющий чертеж справа). В этом случае мы получаем систему равных отрезков: 1-a = 1-13, 2-a = 2-13, 3-a = 3-13, … (чертеж слева). Наибольший интерес здесь вызывает кривая раковинообразной формы («жирная» дуга 16-1-2-3-…, если начинать счет снизу и продолжать по часовой стрелке). Дюрер подробно разъясняет также, как построить кривую яйцеобразной формы.

Он пишет: «Теперь я хочу научить, как строить линию, которая подобна хорошо очерченному яйцу» (левый рисунок). Сначала поводится горизонтальная прямая ab и делится на 10 равных частей. Затем опорная ножка циркуля устанавливается в середину отрезка (точка 5) и проводится окружность так, чтобы она прошла через точки 3 и 7. Дуги 7-d-e и 3-c-e прочерчиваются циркулем, когда его опорная ножка устанавливается в точки a и b, соответственно. Точка f (g) получается делением дуги окружности 3-10 (7-10) ровно пополам. Устанавливая опорную ножку в точку f (g), прочерчивают дугу dh (ch). Наконец, отрезок 10-h делят пополам и из получившейся точки i скругляют острый конец яйца.

Справа от яйцеобразной кривой вычерчена еще одна кривая, которая получается путем пропорционального поднятия правого конца изначально горизонтального отрезка b-d. Отрезок 1-1 уже не параллелен b-d; наклон отрезка 2-2 заметен еще больше. В результате последовательного приподнимания правого края отрезок 19-19 становится вертикально. Однако процесс построения на этом не завершается: точка a оказывается уже по другую сторону от вертикальной линии. Вычерченная кривая, как и кривые яйцеобразной или раковинообразной формы, применяется в архитектуре.

Дюрер рассмотрел множество задач на построение, начиная с самых простейших: деления дуги пополам и проведения перпендикуляра к середине отрезка. Часть этих задач, несомненно, взята из «Начал» Евклида, но выше рассмотренные задачи указывают на дальнейшее развитие евклидовой геометрии, осуществленное Архимедом, Эратосфеном и Аполлонием Пергским, а также математиками Средневековья, занятыми в основном проблемами архитектуры.

Как это обычно бывает, интересные геометрические задачи заставляли «азартных» теоретиков часто выходить за узкие рамки практического применения геометрии в архитектурном строительстве, и находить несколько решений трудных задач ради самих этих задач, без всякой видимой пользы. К такой математической «забаве» можно отнести группу решений на построение улиткообразной линии, т.е. спирали.

Дюрер привел шесть способов построения «улитки» — явно избыточное количество, свидетельствующее о его тяге больше к теории данного вопроса, чем к ремесленническому обучению будущих строителей. Вряд ли он придумал хоть один из них, но сам факт сбора такого количества готовых решений говорит об имеющемся у автора устойчивом интересе к абстрактной математике.

Первый способ был предложен еще Архимедом, хотя Дюрер не ссылается на античного математика, а лишь излагает процедуру построения по его методике. «Сначала, пишет он, — я черчу вертикальную линию, вверху обозначенную через а, внизу — через b, и делю ее тремя точками с, d и е на четыре равные части. Затем я делю de пополам и обозначаю центр через f. Левую часть чертежа я обозначаю через g, правую — через h. Затем беру циркуль, помещаю его ножки в точки d и а и провожу дугу со стороны h до точки b. Вслед за этим помещаю ножки циркуля в точки f и c и провожу дугу со стороны g до точки b и снова беру циркуль, ставя его ножки в точки d и c, и провожу со стороны h до точки e. Далее ставлю одну ножку в f, другую в d и провожу со стороны g до e. Помещаю циркуль на вертикальную линию ab одной ножкой посредине между d и f, а другой — в точку d, а затем провожу дугу со стороны h до точки f. Таким образом, линия готова.

Я могу ее использовать для разных вещей, и, между прочим, она полезна для украшения капители колонны. Чтобы сделать этот метод ясным, я начертил две прямые горизонтальные линии, кончающиеся в точках a и c, из которых начинается спиральная линия» [2, c. 110-111].

Дюрер написал также, что спиральные линии могут быть использованы для вычерчивания епископского посоха и побега с листвой.

Второй способ вычерчивания «улитки» тоже изложен в трактате Архимеда «О спиралях». Суть его пересказана Матвиевской следующим образом: «Чертится окружность произвольным раствором циркуля, соответствующим желательному размеру спирали. Проводится вертикальный радиус аb и, начиная от точки b, на окружности откладывается двенадцать равных дуг, концы которых обозначаются точками 1, 2, 3,. .. ..., 12. Радиус аb подразделяется на двадцать четыре равные части точками, также обозначенными через 1, 2, 3,,.., 24. Дюрер предлагает нанести эти точки на линейку, которую затем следует поворачивать вокруг точки а, в которой линейка закреплена, а второй ее конец последовательно помещать в точки 1,2,3... Когда она занимает положение а1, то на бумаге отмечается точка, соответствующая точке 1 на линейке. В положении а2 будет отмечена точка 2. Таким образом, поворачивая радиус и отмечая каждый раз длину, на одно деление большую, чем предыдущая, получают 23 точки искомой спирали. Если разделить окружность и радиус соответственно на большее число частей, чертеж можно сделать точнее» [2, c. 112].

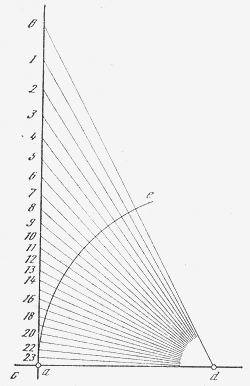
Третий способ является модернизацией второго. «Предлагается рассмотреть, — пишет Матвиевская, — вертикальный радиус аb и горизонтальную прямую cd, соединив затем точки b и d прямой. Взяв точку d в качестве центра, нужно описать радиусом ad дугу окружности ae, разделить эту дугу на 24 равные части и провести через d и точки деления прямые до пересечения их с ab в точках 1, 2,3,..., 23. Расстояния между этими точками неодинаковы: они уменьшаются по направлению к точке a.

Затем следует та же операция, что и в предыдущем случае: радиусом ab описывают окружность, делят ее на 12 равных частей в точках 1, 2,3 . .., 11 и на каждом из радиусов, проведенных в точки деления, отмечают соответствующую ему точку на радиусе ab предыдущего чертежа» [2, c. 113].

Четвертый способ: вычерчивается сектор abc, дуга которого делится на 12 частей. Через точки 1, 2, 3,… 11 проводятся вертикали. «Таким образом начерчена,— пишет Дюрер,— первая основа». Под сектором abc располагается полуокружность с центром с и тем же радиусом, что у сектора. Ее дуга делится на 12 равных частей «Затем следует взять циркуль, поместить одну ножку в точку b квадранта, а другую — в точку 1 линии bc. Этим расстоянием из центра c на нижнем чертеже проводится дуга окружности от вертикальной линии ac до радиуса 1c, и точка пересечения обозначается через 1. Та же операция повторяется относительно точки 2 на линии 2c, и получается точка 2 на радиусе 2c. Продолжая таким образом дальше и соединяя полученные точки, чертят спираль, проходящую от a до c» [2, c. 114].

Пятый способ: радиус a12 делится на 36 равных частей. Опорная ножка циркуля ставится в точке a и прочерчиваются дуги радиусом 1-a, 2-a и т.д. Затем с помощью лекал по часовой стрелке проводится жирная линия спирали, как показано на рисунке.

Шестой способ аналогичен пятому, только более грубый: радиус делится на 8 равных частей, а окружность — на 6 равных секторов.

Третий и четвертый способы построения спиралей генетически связаны с построением разверток, показанных на следующих рисунках: для спирали Архимеда (слева) и просто для окружности, т.е. синусоида (справа).

От этих разверток рукой подать до построения конических сечений — эллипса, параболы и гиперболы, которым античный математик Аполлоний Пергский (250 – 190 гг. до н.э.), современник Архимеда (287 – 212 гг. до н.э.) и Эрастофена (275 – 195 гг. до н.э.), посвятил целый трактат. Авторство ортогональных проекций эллипса и параболы обычно приписывается Дюреру, хотя он, по-видимому, пользовался результатами построения своих предшественников.

Дюрер не сам выдумывал способы вычерчивания спиралей; очевидно, он перенял их у своих предшественников. Здесь мы видим, как через военную технику научные идеи перекочевали сначала в живопись, а затем в начертательную геометрию.

Таким образом, наука существовала всегда, если под ней понимать здравый, более или менее обоснованный взгляд на окружающий нас мир. Ее можно рассматривать либо с индивидуальной (психологической) точки зрения, либо с коллективных (социальных) позиций, когда рассматривается институциональная база как некое государственное учреждение, предназначенное для исследовательских и образовательных целей. Нынешние европейские институты науки в виде университетов и академий возникли во времена Ренессанса, пик которого приходится на период XIV – XVI вв., однако в древние времена научные организации мало чем отличались от современных.

Наука — в самом широком ее смысле — есть свободомыслие . Всякое ее ограничение в форме той или иной религиозности, препятствующей появлению нового знания, является идеологией, которая носит черты догматической косности (см. Романтика: её истоки и природа). Главным препятствием для науки является коллективное мифотворчество, складывающееся из «научных» представлений большого числа людей, далеких от действительно научных исследований. Отсюда возникает постоянное противоречие между новым и старым, которое трансформируется в противоречие между творчески мыслящим индивидуумом и чуждым ему коллективом нетворческих людей.

Идеальное, абсолютно чисто научное знание не может быть признано никаким коллективом посторонних людей, не принимавших непосредственного участия в получении новых знаний. Как только научное знание поступает на службу обществу, оно тут же приобретает — пусть в самом небольшом количестве — догматические черты, препятствующие появлению очередных новых знаний. Выход из этого противоречия, кажется, есть только один — полная изоляция ученого от общества.

Все серьезные научно-исследовательские корпорации, не занимающиеся образовательной деятельностью, по идее, должны быть закрытого типа (см. Корпоративизм). Как только ученый начинает контактировать с непрофессиональной публикой, он фактически перестает быть исследователем. Профессиональная корпорация обязана как можно скорее избавиться от такого «публичного» ученого. Такая тактика вытекает, в частности, из горького урока, связанного с теорией относительности и квантовой механикой, которыми посредством популяризаторов овладели «темные массы».

Однако с появлением Интернета ситуация радикальным образом поменялась. Теперь исследователь может свободно обнародовать свои результаты научного поиска для ознакомления широкого круга пользователей, не занимаясь, собственно, образовательной деятельностью этих ужасных «темных масс», извращающих науку. Всякий желающий вправе воспользоваться новым знанием, не превращая его в идеологию больших коллективов людей, влияющих на поведение исследователя. При отсутствии обратной связи со стороны коллектива на творческую личность добытая научная информация легко видоизменяется.

Таково положение дел в принципе, но в реальности ситуация выглядит иначе. Так, в нашей стране наивысшие академические посты обычно занимают «управленцы», «организаторы» поиска научных знаний, не занимающиеся индивидуальным творческим поиском, но тесно общающиеся посредством телевидения с «темными силами». Они умело лавируют среди множества восходящих и нисходящих тенденций, сформированных за рубежом, в основном, Соединенных Штатах.

Если иметь в виду современное естествознание, то его основание было заложено авторитетами периода кризиса физики начала XIX – конца XX века, поднятыми на гребень популярности «темными массами», поверившими в фантастическую картину мира, искаженную пространственно-временными искривлениями. Вся новизна нынешних «научных теорий» главным образом проистекает из новых экспериментальных наблюдений, которые, однако, ложатся на старую формально-спекулятивную догму.

О нынешнем Конце науки на сайте Sceptic-Ratio говорилось много, сегодня мы обратились к истокам современной цивилизации, пытаемся обратить внимание читателей на начало науки. Возможно, это позволит понять, почему гибнет современное естествознание и что необходимо сделать, чтобы предотвратить катастрофическое разрушение науки.

---

1. Массачусетские архимеды сожгли триеру римлян светом Солнца / www.membrana.ru / mycityua.com/science/global/p1.html, а также: Сергей Викторович Житомирский. Архимед: Пособие для учащихся. – М.: Просвещение, 1981; Житомерский С., Суслович Н., "Наука и жизнь", 1974, №10, http://www.n-t.ru/ri/zh/ar.htm / http://news.spbplus.ru/fakt5.php / Архимед и Марцелл / www.kapfagen.ru/bitva_za_bitvoi/arhimed_i_marcell.html и т.д.
2. Матвиевская Г.П. Альбрехт Дюрер — ученый. — М.: Наука, 1987.
3. Дюрер А. Трактаты. Дневники. Письма. 2-е исправленное издание. СПб.: Азбука, 2000.