Конец науки

Акимов О.Е.

11. Критика Андрея Радзюкевича (I)

• Красота не связана с золотым сечением
• Лука Пачоли в свете спора Стахова с Радзюкевичем
• Неправедная жизнь Луки Пачоли

Красота не связана с золотым сечением

Радзюкевич Андрей Владиславович — кандидат архитектуры, доцент кафедры «Компьютерные технологии проектирования». Закончил архитектурный факультет Новосибирского инженерно-строительного института. Работает директорам Центра довузовской подготовки Новосибирской государственной архитектурно-художественной академии (НГАХА). Обладатель диплома 1 степени регионального конкурса «Золотая капитель». Организатор региональных олимпиад по детскому художественному творчеству. Автор проекта Детская художественная галерея «Прикосновение волшебства» (http://timeart.ru/). Этот проект направлен на формирование открытых выставочных площадок — галерей, как важнейшего элемента системы начального художественного образования в Новосибирске и Новосибирской области; комплексной системы поддержки и развития выставочной деятельности детского художественного творчества. Член жюри по отбору лучших детских художественных работ. Автор ряда статей о законах красоты в архитектуре.

*
*   *

Фрагмент Отзыва ведущей организации на диссертацию А.В. Радзюкевича на тему «Методические основы проведения пропорционального анализа форм памятников архитектуры», представленной на соискание ученой степени кандидата архитектуры

«… Идея закономерного пропорционирования, особенно с использованием отношения золотого сечения, все еще воспроизводится в качестве теоретического постулата, однако, уже не принимается на веру молодыми поколениями архитекторов и не находит применения в их проектной практике. Поэтому нельзя не признать, что потребность в серьезной критической работе, посвященной методическим основам проведения пропорционального анализа форм памятников архитектуры, давно назрела.

В первой главе диссертации А.В. Радзюкевича проводится детальный разбор всех основных направлений пропорционального анализа произведений архитектуры. Его отличает высокий уровень проработки, строгая обоснованность, научная корректность и убедительность выводов. Здесь хорошо показано, что золотое сечение, хотя и может претендовать на роль универсальной закономерности гармонического построения форм, но до сих пор остается в этом отношении неразгаданной тайной, а, следовательно, и неэффективным инструментом в руках архитектуроведов. В то же время увлечение «золотом» и другими иррациональными соотношениями величин привело к неоправданному умалению значимости целочисленных модульно- метрологических систем пропорционирования, которые имели огромный авторитет в древности. Таким образом, обосновывается целесообразность выбора в качестве приоритетного направления исследований именно последнего, целочисленно-модульного.

Во второй главе разбираются методические особенности проведения пропорционально-метрологического анализа форм памятников архитектуры.

Здесь обращают на себя внимание сравнительно-статистические сопоставления пропорций и размеров больших групп памятников. Весьма продуктивен предлагаемый автором автоматизированный метод вариантного моделирования. Убедительно поставлена проблема определения критериев истинности и механизм отбора наиболее вероятного варианта пропорционального строя избранного памятника. Особенно важно то, что автор делает акцент на отыскании документальных свидетельств использования в построении исследуемых памятников соответствующих мер длины и модульных величин, с чем и соотносит геометрические анализы форм.

Для успеха дела необходимо реконструировать, по мере возможности, сам творческий метод разбивки плана здания и определения вертикальных размеров: нам очень плохо известно, как определяли габариты — в свету или в осях, от фундамента или от чистого пола и до основания перекрытия или до самого венчания? Представляется, что предлагаемый А.В. Радзюкевичем методический анализ в совокупности с автоматизировано-статистическим позволит существенно продвинуться в разработке этих вопросов.

Главы третья и четвертая посвящены апробации выдвинутых и разработанных автором методов сравнительно-статистического анализа и автоматизированного вариантного моделирования на примерах ордерных систем древнегреческой дорики и отдельных памятников архитектуры античности. Эта апробация состоялась вполне. Она дала массу очень ценных конкретных наблюдений и привела к весьма существенным заключениям.

Автору удалось установить тот факт, что в античной Греции не было того единообразия модульного и пропорционального построения ордерных форм, о котором писал Витрувий и тем более его комментаторы. Но в императорском Риме тенденция к такому единообразию улавливается. Причем, как отмечает А.В. Радзюкевич, единообразными делались пропорции разных ордеров — дорического (тосканского), ионического и коринфского, что сводило их узнаваемые черты лишь к декоративным мотивам.

Весьма интересны, точны и убедительны авторские исследования размерного и пропорционального построения Парфенона, Пропилеев, храма Ники Аптерос, Эрехтейона, а также и некоторых других храмов классической Греции, внимательно рассмотренных по отдельности и в сравнении между собой. Особой заслугой автора является выявление преемственной связи между построением Старого и Нового Парфенонов, а также анализ построения Эрехтейона в соотнесении с уникальным историческим источником – Сметой строительства Эрехтейона, который доказывает, что размеры классических памятников соответствуют мерам дорической системы.

Ярким завершением всей работы служит авторский анализ пропорционально-метрического построения Пантеона. В нем показана универсализация пропорций ордера в Древнем Риме вне зависимости от его абсолютных размеров, что противоречит положениям трактата Витрувия. Анализ дал основания предполагать, что портик Пантеона был спроектирован одновременно с основным объемом здания. Но самое интересное наблюдение А.В. Радзюкевича, основанное на изучении не только античных, но и средневековых, в том числе древнерусских памятников архитектуры — это факт кратности диаметров круглых купольных форм семи единицам, что давало возможность целочисленного выражения значения иррационального числа «пи» позволяло строить окружности с помощью числа и меры.

Второй том диссертации А.В. Радзюкевича, включающий рисунки и таблицы, поражает объемом графических и расчетных материалов, скрупулезностью их выполнения и доказательностью выдвигаемых автором научных положений. Совершенно очевидно, что представленная диссертация — плод многолетней трудоемкой, тщательнейшей работы автора — великого энтузиаста и тонкого специалиста в своей области. …».

Отзыв составил: доктор архитектуры, член-корреспондент РААСН, зам. директора по научной работе НИИТАГ И.А. Бондаренко.

Защита кандидатской диссертации состоялась 24 июня 2004 года.
Полная весрия Отзыва опубликована 01.07.2004 на сайте
http://www.sibdesign.ru/

*
*   *

Радзюкевич стал критиковать гармонистов-золотоискателей школы Стахова намного раньше, чем Белянин и Василенко, причем его претензии к стаховцам касались существа учения о всеобщей гармонии и золотом сечении (ЗС), а не только каких-то отдельных исторических момментов. Он отрицает саму связь эстетической категории прекрасного с делением отрезка в крайнем и среднем отношении, т.е. с иррациональными числами 0,618 и 1,618. Этот «радикализм» привел его к полному отрицанию золотого сечения как особой пропорции, «ласкающей глаз». Он также освободил историю архитектуры и живописи от золотой пропорции. Ее наличие в древних постройках или в зданиях, возведенных в эпоху Возрождения — факт скорее случайный, чем закономерный.

Летом 2002 года на сайте СибДИЗАЙН.ру появилась его статья «Красивая сказка о "золотом сечении"», которая получила широкий резонанс сначала в среде архитекторов, а затем у многочисленных посетителей сайта «Академия Тринитаризма», где ее разместили 17 февраля 2006 года. Статья начиналась словами: «Около 20 лет назад у меня возник интерес к проблеме золотого сечения в архитектуре и искусстве...» [1]. Оставим на время архитектуру, сосредоточимся на живописном искусстве, точнее, на творчестве Леонардо да Винчи (1452 – 1519). Меня заинтересовала в этой статье фраза: «в трактатах теоретиков эпохи Возрождения, в том числе и в трактатах и записках Леонардо да Винчи, пропорция золотого сечения не нашла никакого отражения» [1].

«Как же так, — подумалось мне, — если этот художник согласился выполнить иллюстрации к трактату Луки Пачоли (1445 – 1514) "О божественной пропорции", он не мог не понимать ее значение, следовательно, где-нибудь в его записях, непременно, что-то сказано по этому поводу. Этот вопрос нужно тщательно изучить», — решил я для себя. У Белянина и Василенко имеются сравнительно «свежие» работы, в которых они с восхищением отзываются о золотой пропорции. Радзюкевича она скорее раздражает, чем восхищает, по причине повышенного к ней внимания со стороны гармонистов-стаховцев.

Правда, мне сейчас не доступна его ранняя статья 1989 года под названием «Золотой блеск модулей Парфенона» [2]. Как видим, словосочетание «золотой блеск» не стоит в кавычках, поэтому не исключено, что в то время автор находил в архитектуре Парфенона золотые пропорции. Но так как этот материал впоследствии вошел в диссертационную работу, в которой критиковалось ЗС, автор статьи [2], видимо, всё-таки в термин «золотой блеск» вкладывал иной смысл, не связанный с золотой пропорцией.

Дискуссия вокруг статьи [1] на сайте СибДИЗАЙН.ру продолжается по сию пору. В середине декабря 2005 году у Радзюкевича состоялся любопытный обмен мнениями с учительницей Еленой Владимировной. На уроках она занималась «развитием творческой деятельности и познавательного интереса учащихся», «формированием практических навыков» у них с целью «закрепления понятия пропорции и основного свойства пропорции» на примере «золотого сечения как частного случая пропорции». Реакция Радзюкевича на ее урок была негативной: «Урок Ваш я прочитал и считаю его научно не обоснованным. Полагаю, что он основывается на ложной гипотезе» (цитируется по записи обсуждения от 11.12.2005, Е.В.).

«Уважаемая Елена Владимировна, — обращается Радзюкевич к учительнице с нарастающим раздражением. — Дело ЗС в надежных руках. Мне жаль, что далеко идущие выводы и привитие детям "понимания и оценки прекрасного в природе и искусстве", выстраивается Вами на содержании книжки Васютинского. Поверьте, что кроме этой работы есть и другие» (12.12.2005, Радзюкевич). «Хочу напомнить Вам, что кроме научно-популярных книжек есть еще академические издания. Например: Зубов В.П. Леонардо да Винчи. М. – Л., 1962 [9]» (14.12.2005, Радзюкевич).

И последняя цитата из диалога с учительницей: «На основании изучения исторических документов, — пишет Радзюкевич, — я констатирую:

1. Художники эпохи Возрождения не использовали золотое сечение в своих работах. Если Леонардо нарисовал несколько геометрических тел в трактате Луки Пачиоли, то из этого не следует, что он взял ЗС в качестве инструмента гармонизации (почитай трактаты Альберти, Дюррера, Палладио, Барбаро, Скамоцци и полное собрание текстов Леонардо).

2. Всякие совпадения в картинах с "золотом" случайны. Возьмите ту картину Леонардо "Мадонна в скалах", которую Вы анализируете на своем уроке. Почему Вы делите картину на две части линией, которая проходит через верх головы мадонны, а не через низ или середину?

3. Линейка и циркуль при рисовании картин в ряде случаев могли быть использованы. Например, при рисовании правильных геометрических тел или при построении перспективы. Но не для того, чтобы разделить картину в золотом сечении.

Самый главный факт — отсутствие этих фактов. Никто, ни один художник или архитектор эпохи Возрождения или античности ни разу не упомянул о золотом сечении и даже не намекнул на ее существование. …» (14.12.2005, Радзюкевич).

Приведу отрывки из работ Радзюкевича, подтверждающие его критическую позицию в отношении истории ЗС: «если обратиться к текстам самого Леонардо, то о "золотой", точнее "божественной" пропорции в них нет ни одного упоминания. Нет даже никаких намеков» [3].

«Кроме того, принципиально важным представляется тот факт, что ни в одном из своих многочисленных текстов, Леонардо ни слова не сказал, ни о "золотом, ни о "божественном", ни о каком-то другом, особенном сечении» [4].

«Во многих популярных изданиях и энциклопедиях утверждается, что в эпоху Возрождения золотая пропорция получила широкое распространение и что ею увлекался сам Леонардо да Винчи. К счастью, есть серьезные исследования по этой теме, которые доказывают историческую неправдоподобность такого "золотого" подхода к искусству эпохи Возрождения. Я имею в виду работы В.П. Зубова и А.И. Щетникова» [5].

*
*   *

Радзюкевич советует учительнице Елене Владимировне и всем нам внимательно читать книгу В.П. Зубова «Леонардо да Винчи» [9]. Что ж, давайте обратимся к ней, а точнее, к первой главе «Жизнь». Цитирую из нее одно предложение, написанное Зубовым: «"Божественная пропорция" — так называемое "золотое сечение", которое интересовало художников и архитекторов того времени ("целое так относится к своей большей части, как большая к меньшей")» [9].

В выделенной курсивом фразе имеются слова «того времени». Уточним: речь идет о пребывании Леонардо да Винчи в Милане, куда он прибыл в 1496 году. В это же году туда приехал Лука Пачоли и они вместе работали над книгой «О божественной пропорции». Вслед за процитированным предложением мы читаем: «В первой части книги Пачоли изложена теория "золотого сечения", во второй — теория правильных многогранников (в которой находит применение "золотая пропорция"). Последняя, третья, часть является трактатом по архитектуре» [9]. И хотя в третьей части, посвященной архитектуре, о золотой пропорции ничего не говорится, трактатом свое название, я думаю, вполне оправдывает.

Чтобы сделать такой вывод, достаточно привести полное называние этой книги, свидетельствующее о намерениях автора: «Божественная пропорция. Книга весьма полезная всякому проницательному и жаждущему знания уму, из которой каждый занимающийся философией, перспективой, живописью, скульптурой, архитектурой, музыкой или другими математическими предметами может приобрести приятные, остроумные и удивительно достойные сведения и найти развлечение по разным вопросам и самым тайным знаниям». Таким образом, автор предполагал, что «золотой пропорцией» могут и должны заинтересоваться живописцы, скульпторы и архитекторы. Третья часть, рассказывающая об архитектуре, но не затрагивающая божественную пропорцию, могла быть включена по другим соображениям. Я имею в виду некоторые особенности характера Луки Пачоли и его манеры работать, о чём будет сказано отдельно.

А пока процитирую абзац из послесловия Я.В. Соколова к «Трактату о счетах и записях» Луки Пачоли; он пишет: «"Божественную пропорцию" украшали пять правильных и несколько полуправильных многогранников, выполненных "божественной левой рукой" Леонардо да Винчи. Интерес Пачоли к правильным геометрическим формам выходил за пределы чистой геометрии и эстетики. Он сочетал одновременно мистицизм и науку, что было нередко в эпоху Возрождения. Восходя к идеям Пифагора и Платона, Пачоли рассматривал правильные геометрические тела как конструктивные основы, составляющие мир. В "Сочинениях Евклида" Пачоли говорил: "Всякий, кто стремится постичь любое искусство, науку или профессию, да поспешит к этой основе (пропорции), от которой проистекает всякое живое знание. И тогда разум его воспарит к звездам"» [15].

С античных времен были известны пять правильных тел Платона — тетраэдр, гексаэдр (куб), октаэдр, икосаэдр, додекаэдр (позиции 1 – 5). Архимед отсек у них углы и получил еще пять полуправильных многогранников. Усеченный тетраэдр состоит из четырех шестиугольных граней и такого же числа треугольных граней. Все грани усеченного тетраэдра правильные, причем сторона шестиугольника равна стороне треугольника. Усеченный гексаэдр состоит из шести восьмиугольных граней и восьми треугольных, а усеченный октаэдр — из шести квадратов и восьми шестиугольников, причем две последние усеченные фигуры имеют равное число вершин, ребер и граней. В таблице многогранников занесены все 13 полуправильных многогранников Архимеда, которые на первом рисунке заняли позиции с 10 по 14. Позиции 12 и 13 занимают ромбокубоктаэдры в двух модификациях, отличающихся поворотом верхней части многогранника относительно его нижней на угол 90°.

Таблица многогранников

Название формы	Позиция рис. 1	f Грани	n Вершины	m Ребра
Тетраэдр	1	4	4	6
Гексаэдр (Куб)	2	6	8	12
Октаэдр	3	8	6	12
Додекаэдр	4	12	20	30
Икосаэдр	5	20	12	30
Усеченный тетраэдр	10	8	12	18
Усеченный гексаэдр	11	14	24	36
Ромбокубооктаэдр	12, 13	26	24	48
Плосконосый куб	14	38	24	60
Усеченный кубооктаэдр	15	26	48	72
Кубооктаэдр	16	14	12	24
Усеченный октаэдр	17	14	24	36
Усеченный додекаэдр	18	32	60	90
Ромбоикосододекаэдр	19	62	60	120
Усеченный икосододекаэдр	20	62	120	180
Икосододекаэдр	21	32	30	60
Усеченный икосаэдр	22	32	60	90
Плосконосый додекаэдр	23	92	60	150
Правильная призма	24	k + 2	2k	3k
Антипризма	25	2k + 2	2k	4k

Многогранники. Платоновы тела (1 – 5), тела Пуансо (6 – 9) и Архимедовы тела (10 – 23). Особый класс образуют параллелоэдры, которыми можно заполнить все бесконечное пространство, не оставляя пустоты и без того, чтобы их внутренние объемы пересекались (26 – 30).

Итак, Зубов утверждает, что художников и архитекторов эпохи Возрождения интересовало золотое сечение или божественная пропорция. По поводу термина «божественная пропорция, которым, по мнению Радзюкевича, Леонардо да Винчи никогда не пользовался — тоже не всё так однозначно. В его «Трактате о живописи», в котором сопоставляются поэзия, музыка и живопись, автор пишет примерно в том же духе, что и античные философы. Подчеркнем, художник эпохи Возрождения имеет в виду не золотое сечение в узко геометрическом смысле как отношение Φ или φ, а более широко, в духе Пифагора и Платона, но термины «гармоническая» или «божественная» пропорция в тексте имеются. Причем узнаем мы об этом из той самой книги Зубова, которую Радзюкевич рекомендовал учительнице Елене Владимировне внимательно прочитать. В главе «Время» мы находим целый каскад любвеобильных слов по поводу предмета, которым восхищаются стаховцы и прочие гармонисты-золотоискатели.

«Музыка и поэзия показывают предмет по частям, живопись показывает его части сразу, одновременно (aunmedesimo tempo). В поэзии происходит "то же самое, как если бы мы захотели показывать лицо по частям, всегда закрывая те части, которые были показаны раньше; при таком показывании забывчивость не позволяет сложиться никакой гармонической пропорциональности, ибо глаз не охватывает их своею способностью зрения одновременно" (Т. Р., 21).

"Поэт не замечает, что его слова, при обозначении членений такой красоты, отделены одно от другого временем, которое разъединяет их забвением и разделяет отношения, не давая возможности обозначить их без долгих околичностей. И не имея возможности их обозначить, поэт не может образовать гармоническую пропорциональность, слагающуюся из божественных отношений, а потому и одновременность (un medesimo tempo), в которую заключено созерцание красоты, написанной на картине, не может быть достигнута описанием красоты в словах" (Т. Р., 23).

Поэт поступает так, как "если бы красивое лицо открывалось тебе часть за частью". "В таком случае ты никогда не останешься удовлетворен его красотой, целиком заключающейся лишь в божественной пропорциональности названных частей, сочетаемых вместе и только одновременно (in un tempo) создающих эту божественную гармонию, которая получается из сочетания частей" (Т. Р., 32).

В уста короля Матвея Корвина Леонардо вложил тот же упрек поэту: "Твое произведение не радует мысль слушателя или зрителя так, как делает это пропорциональность прекраснейших частей, из которых слагаются божественные красоты находящегося передо мною лица и которые, сочетаясь друг с другом вместе, в одно время (in un medesimo tempo), приносят мне своей божественной соразмерностью столько радости, что, думается мне, ни одна вещь на земле, созданная человеком, не способна дать больше" (Т. Р., 27). ...

В отличие от поэзии в музыке возможно и одновременное гармоническое созвучие. В этом отношении музыка ближе к живописи, и потому Леонардо называет ее "сестрой живописи" (Т. Р., 29). В живописи "получается гармоническое отношение, так же как много различных голосов, сочетаясь друг с другом в одно и то же время (in un medesimo tempo), дают гармоническое отношение, которое настолько удовлетворяет чувство слуха, что слушатели пребывают в изумленном восхищении" (Т. Р., 21)» [9].

*
*   *

«Еще один момент, — обращает внимание Радзюкевич на сомнительную цитату Елены Владимировны. — Вы пишете: "Сегодня на уроке мы попытаемся разгадать один из секретов Леонардо да Винчи, ведь именно ему принадлежат слова: Кто не знает математики — пусть не пытается разгадать мои картины!". Скажите, в каком именно тексте Леонардо есть такие слова? Я просмотрел все Рихтеровское издание всех текстов Леонардо и ничего подобного не нашел. Буду очень признателен» (12.12.2005, Радзюкевич).

Поскольку учительница не смогла ответить на вопрос, откуда взялась фраза «Кто не знает математики — пусть не пытается разгадать мои картины», я, хоть и с большим опозданием, попытаюсь ответить на него, насколько это возможно. В указанной Радзюкевичем книге Зубова о Леонардо да Винчи, глава «Рай математических наук» начинается следующими словами:

«"Пусть не читает меня тот, кто не математик", — заявлял Леонардо (W. An. IV, 14 об., стр. 12). Математические науки (арифметика и геометрия) обладают, по его словам, высшей достоверностью, накладывают "молчание на языки спорщиков", приводят "к вечному молчанию" всякое возражение, прекращают ненавистный Леонардо крик (Т. Р., 33, стр. 9 – 10). "Тот, кто порочит высшую достоверность математики, тот питается сумбуром и никогда не заставит умолкнуть противоречия софистических наук, которые учат вечному крику... " (W. An. II, 14, стр. 20)» [9].

Это не точное воспроизведение слов, приведенных учительницей, но все-таки достаточно близко передает позицию художника в отношении математики. Вот выдержка из статьи Радзюкевича, рассказывающая нам о том, каким неважным математиком был Леонардо да Винчи: «Для него, как для пытливого исследователя-практика, абстрактная математика играла вторичную роль. По заключению В.П. Зубова "Леонардо довольствовался чаще всего приближенными решениями, достаточными для инженера, но не удовлетворяющими требованиям математической строгости" [9]. Его математические выкладки "почти всегда просты — неизмеримо проще, чем те широкие и сложные задачи, которые он ставил и которые не могли быть с исчерпывающей полнотой решены средствами старого математического аппарата" [там же]» [3].

Никто и никогда не считал Леонардо великим математиком эпохи Возрождения, но упрекать его в пренебрежительном отношении к ней было бы неправильно. Из книги Зубова можно надергать что угодно, но, мне кажется, даже этот скептически заряженный автор не хотел создать у читателей впечатлений, будто для Леонардо «абстрактная математика играла вторичную роль». У меня сложилось впечатление, что Зубов пытался доказать, что Леонардо высоко ценил математику, но использовал ее достаточно утилитарно, в прикладных задачах, до конца не осознавая ее превосходство в абстрактном виде.

После приведенного мною начала главы «Рай математических наук» Зубов пишет: «Кажется, все ясно. Математика и механика провозглашены двумя верховными науками — Леонардо не только "предтеча" механико-математического миросозерцания, но и первый его представитель. На самом деле вопрос сложнее, чем это кажется.

Прежде всего, когда Леонардо говорил о механике, он понимал под этим словом не теоретическую дисциплину, а практическое применение теоретических положений. Именно потому он и говорил, что посредством механики "достигают математического плода". Книгам, которые Леонардо проектировал, он давал заглавие не "Механика", а "Элементы машин" или, точнее, "Начала построения машин" (Elementi rnacchinali) — по образцу "Начал" Евклида (А, 10, стр. 84); он также упоминал “Книгу о науке машин” (libro della scientia delle machine, W. An. I, 13 об., стр. 84)» [9].

Леонардо да Винчи. Итальянцы, перечисляя, кем был для них этот великий человек, называют следующие его профессии: архитектор, музыкант, анатом, изобретатель, инженер, скульптор, геометр и живописец эпохи Возрождения.

Далее читаем: «Леонардо прямо противопоставлял "механическое доказательство" (prova meccanica) "механике". "Доказательство это тем более достойно похвалы, — говорил он, — чем более непосредственно, само собою, дает ту же самую истину, какую дает и механика" (С. А., 231а, стр. 84—85). Совершенно очевидно, что слово "механика" здесь употреблено в значении "механического искусства". Благодаря "механике" реализуются теоретические положения "математики", которая включает и то, что мы теперь называем теоретической механикой.

Что "математика" охватывала у Леонардо не только чисто математические дисциплины, но и физику, явствует из его восклицания: "О математики, пролейте свет на это заблуждение! Дух не имеет голоса, ибо, где голос, там тело... " и т. д. (см. ИП, стр. 19). Очевидно, что не математики, а физики (в современном значении слова) занимаются вопросами акустики, а потому и призваны опровергать разглагольствования о "голосах духов". Когда Леонардо утверждал, что "птица — действующий по математическому закону и инструмент" (С. А., 161а, стр. 596), он опять-таки явно имел в виду не математику, а то, что теперь называется механикой.

Может показаться, что от такого переименования механики (или физико-математических наук в целом) в математику существо дела не меняется. Идеал математико-механического описания и объяснения природы как будто остается в обоих случаях тем же. На самом деле это не так.

Требование "пусть не читает меня тот, кто не математик" ведь уже не относится тогда к чистой математике или к математике в строгом значении слова. Иной смысл получает и другой афоризм Леонардо: "Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой" (G, 96 об., стр. 12). Это вовсе не то же самое, что заявление Канта: “Я утверждаю, что в каждой специальной естественной науке можно найти собственно науки лишь столько, сколько в ней математики". У Леонардо речь идет о физико-математических науках, у Канта — о математике как таковой.

Leonardo da Vinci, 1452 – 1519

Чтобы окончательно убедиться в этом, попробуем пересмотреть еще раз приведенные и некоторые другие высказывания Леонардо да Винчи уже не так, как они даются обычно в антологиях, вне контекста, а в связи с тем конкретным поводом, который побудил к ним. "Пусть не читает меня тот, кто не математик",— было сказано при описании механизма сердечных клапанов. "Тот, кто порочит высшую достоверность математики", — было сказано опять в связи с рисунком сердца. "А потому, об изучающие, изучайте математику и не стройте без фундаментов", — после длинного рассуждения о движениях при дыхании и пищеварении (W. An. IV, 14 об.). "Все это я опишу и нарисую подробно, доказывая эти движения на основе моих математических начал", — о движении мускулов рта (W. An. В, 29)» [9].

В этих рассуждениях Зубова, к которому прислонился Радзюкевич, много субъективного, надуманного и неубедительного. По-моему, название «Начала построения машин» — по образцу «Начал» Евклида — не является аргументом против «теоретической дисциплины» в пользу «практического применения теоретических положений». Во всяком случае, я бы не стал выставлять столь слабый довод на первое место.

*
*   *

Теперь по поводу эпиграфа к указанной главе: «Механика — рай математических наук, посредством нее достигают математического плода» и передающего примерно тот же смысл предложения Леонардо: «Доказательство это тем более достойно похвалы, чем более непосредственно, само собою, дает ту же самую истину, какую дает и механика». Зубов, очевидно, не знает позиции Архимеда по этому вопросу.

В письме к Эратосфену знаменитый античный математик и механик пишет: «... Я счел нужным написать тебе и в этой же самой книге изложить некоторый особый метод, при помощи которого ты получишь возможность при помощи механики находить некоторые математические теоремы. Я уверен, что этот метод будет тебе ничуть не менее полезен и для доказательства самих теорем. Действительно, кое-что из того, что ранее было мною усмотрено при помощи механики, позднее было также доказано и геометрически, так как рассмотрение при помощи этого метода еще не является доказательством. Однако получить при помощи этого метода некоторое предварительное представление об исследуемом, а затем найти и само доказательство, гораздо удобнее, чем производить изыскания, ничего не зная» (см. седьмой подраздел «Конструктивной математики»).

Приходится только удивляться, насколько одинаково мыслят величайшие умы Античности и Ренессанса. Может быть, Зубов сомневается в математических способностях Архимеда? Он, наверное, не знает, что Ньютона современники считали великим геометром, а не физиком, и вообще, нельзя ставить в вину математику то, что он апеллирует к механике и, наоборот. Это настолько тесно связанные науки, что всякое противопоставление их чревато бессмысленным пустозвонством. Зубов встал на этот путь, чем доказал свою некомпетентность в математике и механике, в их истории и истории науки вообще. Всё в его доказательствах шатко, вымучено и высосано из пальца.

Так, мы читаем превосходное высказывание Леонардо: «Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой». Аналогичное высказывание есть у Канта: «Я утверждаю, что в каждой специальной естественной науке можно найти собственно науки лишь столько, сколько в ней математики». Вместо того, чтобы порадоваться насколько сходно мыслят великие мыслители разных эпох, Зубов вдруг решает: «У Леонардо речь идет о физико-математических науках, у Канта — о математике как таковой».

Статуя Леонардо да Винчи, автор Луиджи Пампалони (Luigi Pampaloni), Флоренция, вблизи Уффици.

Во-первых: из чего это следует? Во-вторых: ну, и что? И Кант, и Леонардо говорят только о математике. Зубов на ровном месте сталкивает их лбами: один, видите ли, имел в виду физико-математические науки, другой — чисто математические. В чём разница между ними, ведь контекст один и тот же? Оба хотели сказать только одно: в науке столько истины, сколько в ней математики. Но так как Зубов пытается доказать, что Леонардо был больше практическим инженером-механиком, чем чистым математиком, он вложил в словосочетания Леонардо «одна из математических наук» смысл одной «физико-математической науки», забыв о том, что Кант вообще не знал математики. Представление философа об этом предмете было наверняка более расплывчатым, чем у знаменитого механика.

Еще раз повторим, Леонардо да Винчи не был большим математиком, с этим никто не спорит, но от души восхищался ею, ставя ее на первое место среди всех прочих наук, включая механику. Так часто бывает и нельзя на этом основании доказывать, что под математикой он имел в виду скорее механику, чем, собственно, математику. В конце концов, проблема заключается в соотношении теории и практики. Леонардо сделал свой выбор: «Влюбленный в практику без науки — словно кормчий, ступающий на корабль без руля или компаса; он никогда не уверен, куда плывет. Всегда практика должна быть воздвигнута на хорошей теории». Эти слова привел, между прочим, Зубов, но свой ложный тезис он доказывает ценой искажения содержания приводимых им цитат, во многом домысливая за автора. Радзюкевич же из его путаных суждений делает далеко идущие выводы, мол, для Леонардо «абстрактная математика играла вторичную роль».

Зубов берет цитату и выворачивает ее так, что читателю кажется, будто Леонардо пренебрегал математикой в пользу механики, причем этот упрек звучит постоянно. Например, в главе «Глаз — повелитель чувств» вдруг, без особой надобности слышим возмущенный вопрос: «И где тогда пресловутый "математизм" Леонардо, коль скоро доподлинному существу живописи нельзя научить, в отличие от математических наук, в которых ученик усваивает ровно столько, сколько прочитывает ему учитель?» [9]. Впору спросить: где здесь логика? По Зубову получается «в огороде бузина, а в Киеве дядька».

Приведу еще один пример непоследовательного мышления из главы «Рай математических наук». Зубов отмечает: «Леонардо проявлял известный интерес к алгебре. Среди его записей можно найти такие заметки для памяти: "Альберт из Имолы, Алгебра, т. е. показание того, как число и неизвестное (cosa) приравниваются к неизвестному числу (cosa numero)" (К, 75 об., стр. 26). Или: "Алгебра, которая находится в семье Марлиани и написана их отцом" (С. А., 225Ь, стр. 26)» [9]. Перевод первой цитаты, видимо, неверный — впрочем, это сейчас неважно. Посмотрите, с кем он тут же решил сравнить прославленного инженера-механика эпохи Возрождения.

Пример псевдонаучного исследования: Иисус Христос или Леонардо да Винчи? Есть люди, которые доказывают, что на ткани Туринской плащанице изображен не Иисус Христос, а Леонардо да Винчи. Между тем нужно еще доказать, что известный рисунок старца является его автопортретом и подлинность плащаницы.

«Но Леонардо да Винчи, — пишет Зубов, — не мог бы никоим образом внести в свои записные книжки заявление, подобное тому, которое 300 лет спустя сделал Лагранж в предисловии к "Аналитической механике" (1788): "В этой работе совершенно отсутствуют какие бы то ни было чертежи. Излагаемые мною методы не требуют ни построений, ни геометрических или механических рассуждений; они требуют только алгебраических операций, подчиненных планомерному и однообразному ходу. Все любящие анализ с удовольствием убедятся в том, что механика становится его новой отраслью, и будут мне благодарны за то, что этим путем я расширил область его применения".

У Леонардо как раз наоборот: его рассуждения требуют чертежей, непонятны без геометрически наглядных образов. Его рассуждения всегда геометрические или геометрико-механические» [9].

Спрашивается, причем здесь «Аналитическая механика» Лагранжа. Леонардо жил совершенно в другую эпоху, в ней и нужно искать людей для сравнения с ним. Кроме того, полистайте «Математические начала» Ньютона, они сплошь усыпаны чертежами. Ньютон был плохим математиком или механиком? И вообще, как можно ставить в вину наличие или отсутствие чертежей? Понятно, что живописца привлекает в математике прежде всего геометрия, т.е. то, что можно увидеть. Символьная алгебра привлекает меньше, но и ею, как видим, Леонардо интересовался.

Общее число чертежей в «Математических началах» Ньютона превышает две сотни; здесь приведены некоторые из них.

*
*   *

Рисуя правильные многогранники в книге Луки Пачоли «О божественной пропорции», Леонардо да Винчи не пользуется циркулем и линейкой. По его записям также видно, что он мало вычислял. Его мышление больше практическое, чем теоретическое, скорее синтетическое и ассоциативное, чем аналитическое и логическое. Тем не менее, оно целиком пронизано количественной мерой, т.е. числовой математикой, которую он связывал с гармонией. Она, конечно, достаточно примитивна, ее невозможно — да и не нужно сравнивать с математикой Лагранжа и Ньютона, зато она вполне сопоставима с математическим восприятием Пифагора и Платона.

«То, что Леонардо да Винчи оформил трактат Луки Пачиоли, нарисовав в нем рисунки правильных многоугольников [наверное, многогранников], — пишет Радзюкевич, — еще ни о чем не говорит. Сами рисунки многоугольников выполнены не совсем точно. Судя по характеру изображений можно сделать вывод, что они не построены геометрически, а нарисованы "от руки"» [4]. Этим аргументом критик хотел, видимо, сказать, что Леонардо выполнил заказ Пачоли формально и даже, может быть, небрежно, во всяком случае, без должного изучения объекта рисования. Постараюсь показать, что это вряд ли верно.

Леонардо всегда относился к своей работе очень серьезно и осмысленно, с максимально возможным старанием, иначе он не брался бы за ее выполнение вообще — таков его характер. Практически нет никаких сомнений, что он рисовал многогранники со сделанных его руками моделей. Лука Пачоли обращает внимание на перспективное представление 60 сделанных им рисунков, что также свидетельствует о большой предварительной работе, проделанной им по изготовлению этих моделей.

В связи с затронутой нами темой Брагина пишет: «Здесь он [Лука Пачоли] вновь воздает хвалу рисункам Леонардо, сделанным для его книги "О божественной пропорции". Леонардо создал прекрасные фигуры многогранников — "высочайшего [уровня] легчайшие [изящные] фигуры всех платоновских и математических тел, как правильных, так и производных [от правильных], рисунки которых выполнил в изометрической перспективе столь совершенно, что лучше сделать было бы невозможно, даже если бы к нам вернулись Апеллес, Мирон, Поликлет и другие". И ностальгически замечает, что Леонардо выполнял рисунки "в те счастливые времена, когда мы вместе находились на службе в восхитительном городе Милане"» [16].

  (1)

  (2)

  (3)

  (4)

  (5)

  (6)

  (7)

  (8)

  (9)

  (10)

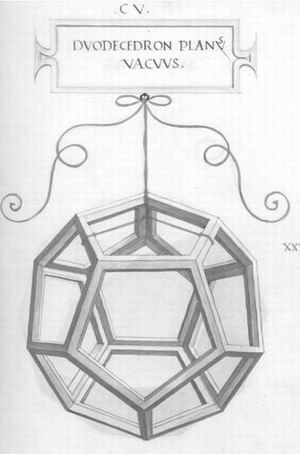
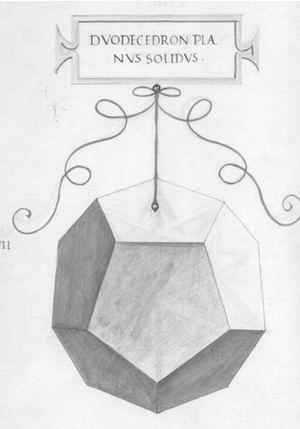
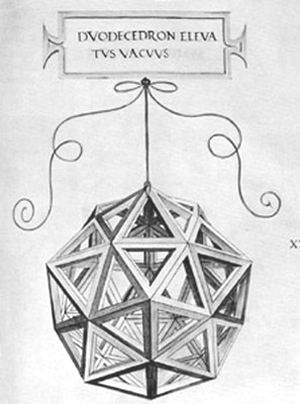
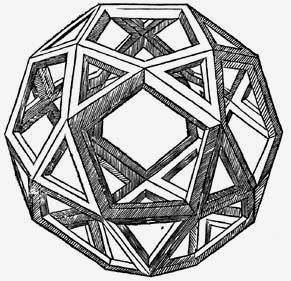
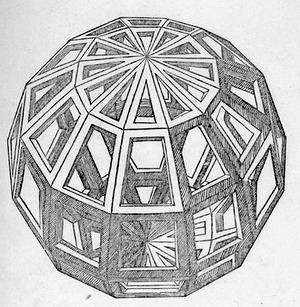
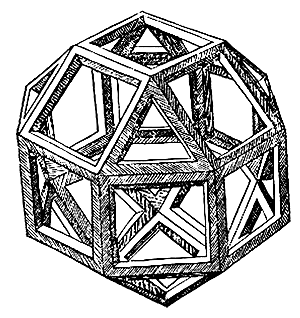
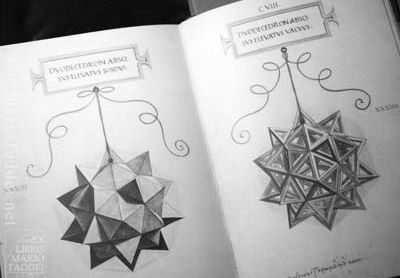
Правильные геометрические тела для трактата Луки Пачоли «О божественных пропорциях» Леонардо да Винчи сначала мастерил из тонких деревянных реек. Затем готовые склеенные модели он подвешивал на шнуре и зарисовывал, как это показано на примере додекаэдра (1) и звездчатого тела Пуансо (3) (см. также выше таблицу многогранников, позиция 7 ). Рисунок «твердого» («soliduus») додекаэдра (2) художник получал из «пустого» («vacuus») додекаэдра (1) путем наложения на стекло с подсветкой и обводкой развернутых к зрителю граней. Точно так же он поступал со всеми другими объемными фигурами. Здесь показаны еще икосододекаэдр (4), звездчатый октаэдр Кеплера или Stella Octangular (5), шестидесятигранник (6) и ромбокубооктаэдр (7). Этот многогранник, сделанный из стекла и наполовину заполненный водой, изображен на картине с Лукой Пачоли (см. ниже). На фотографии (8) показано здание Белорусской государственной библиотеки (Минск), построенное в форме ромбокубооктаэдра. Позиции (9) и (10) занимает еще одно звездчатое тело, которое является, по-видимому, свободной фантазией Леонардо да Винчи. Общее число моделей, изготовленных им из деревянных реек, равно 59. Именно они послужили основой для трактата «О божественной пропорции».

Рассказывая о Леонардо, историк живописи эпохи Возрождения Джорджо Вазари (1511 – 1574) обращает внимание читателей на его большую любовь к моделированию и рисованию чертежей: «Рисовал он и на бумаге столь тщательно и так хорошо, что нет никого, кому в этих тонкостях когда-либо удалось с ним сравняться… Он ежедневно делал модели и чертежи, чтобы показать, как возможно с легкостью сносить горы и прорывать через них переходы из одной долины в другую и как возможно поднимать и передвигать большие тяжести при помощи рычагов, воротов и винтов, как осушать гавани и как через трубы выводить воду из низин, ибо этот мозг никогда в своих измышлениях не находил себе покоя, и множество рисунков со следами подобных его мыслей и трудов мы видим рассеянными среди наших художников, да и сам я видел их немало. … Среди его моделей и чертежей был один, при помощи которого он неоднократно пытался доказать многим выдающимся гражданам, управлявшим в то время Флоренцией, что он может поднять храм Сан Джованни и подвести под него лестницы, не разрушая его…» [14, с. 211 – 212].

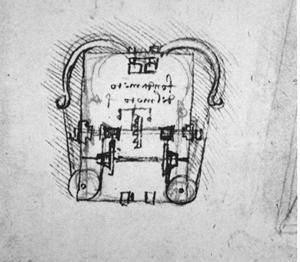
Большинство чертежей, включая чертежи сложных механических узлов, Леонардо да Винчи рисовал от руки, без применения линейки и циркуля. Однако это ни в коем случае не снижало качество предложенного им механизма. В наши дни по его рисункам многие музеи истории науки и техники смогли воссоздать действующие модели. Здесь приведены рисунки двух механизмов и фотографии соответствующих моделей. Первый механизм представляет собой систему зубчатой передачи; второй напоминает анкерный механизм для часов (leaf-spring clock drive).

Радзюкевич абсолютно не представляет себе манеру работы Леонардо да Винчи совместно с другими творческими людьми. Художник не просто слепо копировал изучаемые ими объекты, а сам активно участвовал в исследовании предмета. В этом можно убедиться на многих примерах. В частности, вылепливая скульптуру «Коня», он попутно делает зарисовки мышц и костей животного, изучает его анатомию и пишет целую книгу по этому предмету. А сколько он работал над анатомией человека, параллельно создавая свои великолепные живописные произведения.

Конь. По наброскам Леонардо да Винча
скульптура была все же отлита в бронзе.

«Погибла также почитавшаяся совершенной небольшая восковая модель, наравне с книгой об анатомии лошадей, составленной им для своих научных занятий, — пишет Вазари. — Засим он приступил, но с еще большим усердием, к анатомии людей, пользуясь в этом деле помощью превосходного философа, читавшего в то время в Павии лекции и писавшего об этом предмете, а именно Маркантонио делла Торре, которому он взамен этого и сам помогал и который был (насколько я слышал) одним из первых, кто начал изучать медицину в свете учения Галена и освещать истинным светом анатомию, остававшуюся до того времени окруженной густым и величайшим мраком невежества. В этом он чудесно использовал гений, труд и руку Леонардо, который составил книгу из рисунков красным карандашом, заштрихованных пером, с изображением трупов, мышц и костей, с которых он собственноручно сдирал кожу и которые срисовывал с величайшей тщательностью. На этих рисунках он изображал все кости, а затем по порядку соединял их сухожилиями и покрывал мышцами: первыми, которые прикреплены к костям, вторыми, которые служат опорными точками, и третьими, которые управляют движениями, и тут же в разных местах он вписывал буквы, написанные неразборчивым почерком, левой рукой и навыворот, так что всякий, у кого нет навыка, не может их разобрать, ибо читать их можно не иначе как с зеркалом. … И тому, кто читает эти рукописи, кажется невозможным, чтобы этот божественный дух так хорошо рассуждал об искусстве, мышцах, сухожилиях и сосудах, причем обо всем с такой обстоятельностью» [14, с. 221 – 222].

После этого невозможно уже говорить, что Леонардо оставался равнодушным к теме золотой пропорции, которая пленила Пачоли.

Анатомические зарисовки

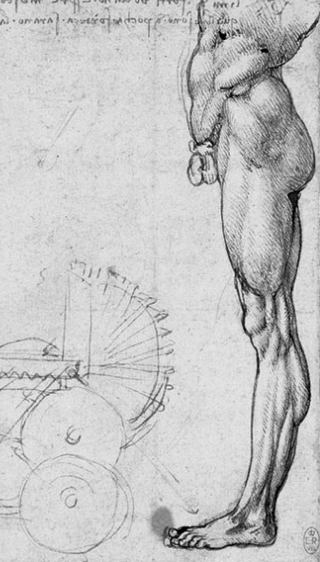
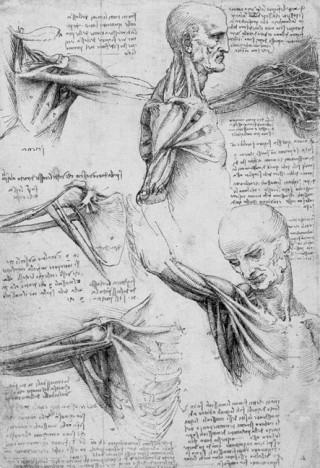
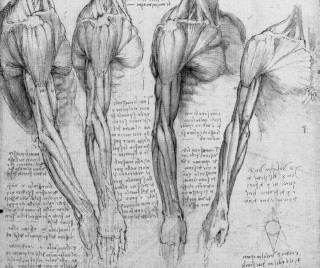
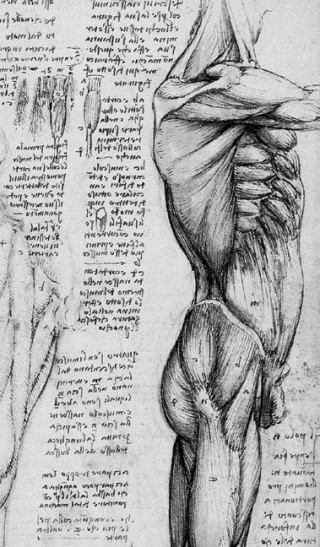
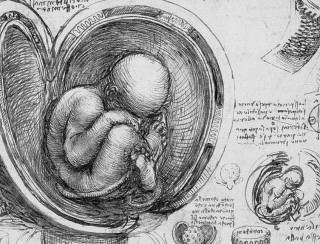
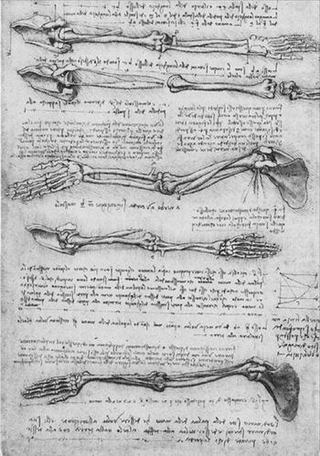
Первый рисунок с изображением мышц ноги относится примерно к 1490 году. Остальные рисунки анатомических исследований мускулов шеи, плеча, груди, руки и т.д., а также плода в матке скелеты рук относятся примерно к 1510 году. Это говорит об устойчивом интересе Леонардо да Винчи к анатомии человека. Последний рисунок с изображением мускулистого тала мужчины выполнил Микеланджело Буонарроти. Однако его интерес к человеческому телу ограничивался чисто художественной стороной дела.

Лука Пачоли в свете спора Стахова с Радзюкевичем

Радзюкевич критиковал не только учительницу Елену Владимировну, авторов «многих популярных изданий и энциклопедий», главным субъектом его критики был и остается Стахов Алексей Петрович. Его позиция на этот счет нам известна (см. подраздел Стахов: древняя парадигма и ее роль в науке), тем не менее, напомним читателям некоторые наиболее яркие заявления директора Института Золотого Сечения по этому поводу.

В одной из основных работ Стахова, которая разбиралась в указанном выше подразделе, говорится: «В эпоху Возрождения продолжаются поиски совершенной пропорции. В работах Леонардо да Винчи и Дюрера учение о пропорциях сводится к поискам идеальной меры человеческого тела ("Витрувийский человек" Леонардо да Винчи). В этот период возрождается интерес к золотому сечению, а Леонардо да Винчи вводит это название в широкое употребление. Под непосредственным влиянием Леонардо в эту эпоху издается одно из самых знаменитых сочинений о золотом сечении. Речь идет о трактате известного итальянского математика Луки Пачоли "О божественной пропорции". Пачоли не случайно вводит в название своего трактата термин божественный. Он совершенно убежден в божественном происхождении золотой пропорции» [6].

Во второй части этой же статьи мы читаем: «Золотая пропорция занимает ведущее место в художественных канонах Леонардо да Винчи и Дюрера. В соответствии с этими канонами золотая пропорция отвечает делению тела на две неравные части линией талии. То есть самый простой вид осуществления Золотого Сечения заключается в том, что все тело линией пупа должно делиться в отношении Золотого Сечения. Точно также при вытянутых по швам руках кончики концы средних пальцев должны весь рост человека делить в отношении Золотого Сечения. Известное правило, что лоб, нос и нижняя часть лица должны быть равны, дополняется тем, что рот делит нижнюю часть тела в отношении Золотого Сечения. Брови делят всю голову в отношении Золотого Сечения и т.д.» [7].

На вопрос Юрия Чёрного, корреспондента журнала «Наука и эзотерическая традиция», Стахов отвечает: «Код да Винчи и Золотая пропорция — это одно и то же понятие. И это подтверждается рядом фактов из научной биографии великого Леонардо. Известно, что Золотая пропорция, пришедшая к нам из египетской и греческой культуры, была объектом увлечения и пристального внимания Леонардо да Винчи. Более того, широким использованием термина золотое сечение европейская культура обязана именно Леонардо да Винчи.

По инициативе Леонардо знаменитый итальянский математик и ученый монах Лука Пачоли, его друг и научный советник, опубликовал книгу De Divina Proportione, первое в мировой литературе математическое сочинение о золотом сечении. Автор назвал его Божественной пропорцией. Известно также, что сам Леонардо иллюстрировал эту знаменитую книгу, нарисовав к ней 60 замечательных рисунков, которые до сих пор сохраняют свою научную и художественную ценность. Именно поэтому эти факты, которые не очень известны широкой научной общественности, дают право выдвинуть гипотезу о том, что Код да Винчи — это не что иное, как золотое сечение. И поэтому авторы книги Код да Винчи и ряды Фибоначчи, посвященной популярному изложению теории золотого сечения и его приложений, и использовали это понятие в названии книги» [8].

Здесь вновь поднимается вопрос о словах «золотое сечение» и «божественная пропорция», который обсуждался выше. Добавим к сказанному, поскольку термин «божественная пропорция» Леонардо да Винчи использовал широко, в смысле «гармонических пропорций» или даже «эстетически прекрасных пропорций», а Лука Пачоли употребил его в узком геометрическом смысле, связав его с именем Евклида, то термин «золотое сечение», возможно, кто-то третий ввел для снятия этого терминологического расхождения.

Как бы там ни было, спор о славах не является для нас столь уж принципиальным. Важнее выяснить вклад каждого — Леонардо да Винчи и Луки Пачоли — в написание трактата «О божественной пропорции» («De Divina Proportione»). Радзюкевич придерживается мнения самого скромного участия первого и максимально второго; Стахов считает наоборот, именно «по инициативе Леонардо» была написана данная книга. Чтобы разрешить спор между Стаховым и Радзюкевичем, нужно представлять себе ситуацию с Евклидом на тот момент, подход к нему Леонардо и выяснить подход Пачоли к написанию научно-просветительских работ.

*
*   *

Решая данную задачу, нам нужно не забывать о великолепных способностях художника ко всем искусствам и наукам, включая математику. В разрез мнению Зубова, с которым мы знакомились выше, Вазари по этому поводу писал: «Поистине дивным и небесным был Леонардо, сын сера Пьеро из Винчи. Обладая широкими познаниями и владея основами наук, он добился бы великих преимуществ, не будь он столь переменчивым и непостоянным. В самом деле, он принимался за изучение многих предметов, но, приступив, затем бросал их. Так, в математике за те немногие месяцы, что он ею занимался, он сделал такие успехи, что, постоянно выдвигая всякие сомнения и трудности перед тем учителем, у которого он обучался, он не раз ставил его в тупик» [14, с. 210].

Под «учителем» Вазари имел в виду, конечно, не Луку Пачоли. В жизнеописании Пьеро делла Франческа он о нем отзывается резко отрицательно. Если бы здесь снова зашла речь о Пачоли, Вазари не стеснялся бы в бранных эпитетах. Учителем Леонардо считается Андре Верроккьо, который по просьбе отца опекал его с 1566 по 1576 год. Он вырос довольно в суровых условиях, без родительской ласки. Это связано с тем, что Леонардо был побочным сыном от некой Катарины, крестьянке из деревни Винчи, а его отец «принадлежал к числу виднейших, зажиточнейших нотариусов Флоренции».

«"Божественная пропорция" — пишет Я.В. Соколов в послесловии к "Трактату о счетах и записях", — подводила итог беседам, размышлениям и дружбе Л. Пачоли с П. делла Франческа, Л. Б. Альберти, Леонардо да Винчи. Это была символическая книга. "Весьма показательно, — писал В.И. Рутенбург, — творческое содружество математика Луки Пачоли с художником Пьеро делла Франческа, которые вместе искали секрет пропорций человеческого тела, найденный древними. Они пришли к открытиям в практике искусства и в теории. Л. Пачоли изучал и вводил в текст своих сочинений советы Витрувия, призывая читателей быть внимательными к ним и усердно запечатлевать их"» [15].

В этом отрывке Рутенбург нарисовал слишком благостную картинку, как учитель и ученик в «творческом содружестве», «вместе искали секрет пропорций человеческого тела». Правда их отношений, по-видимому, была не столь идиллической. Вот как начинает описывать Вазари биографию Пьеро делла Франческа.

«Поистине несчастны те, которые утомляют себя изучением, чтобы помочь другим и оставить по себе славу, а сами порою из-за болезни или смерти не могут довести до завершения начатых ими работ. И часто случается, что труды их, оставленные ими немного неоконченными или почти законченными, оказываются захваченными дерзостью тех, которые пытаются прикрыть свою ослиную кожу почетной шкурой льва. Хотя время, которое зовется отцом истины, рано или поздно обнаруживает правду, но все-таки случается, что на некоторое время бывает обманно лишен почестей тот, кто заслужил их своими трудами.

На одной из своих картин, а именно, «Воскрешение», где нарисован воскресший Иисус Христос, стоящий над спящими римскими солдатами, Пьеро делла Франческа (1419-1492) изобразил себя. Деталь картины с автопортретом художника ниже показана крупно; рядом с ним лицо Иисуса Христа. Франческа — автор математических трактатов «О перспективе в живописи», хранящийся ныне в Амброзианской библиотеке (Милан) и «Книги о пяти правильных телах». В Википедии сообщается, что этими книгами он снискал гораздо больший авторитет в XV — XVII вв., чем живописью. Помиму Луки Пачоли он был учителем знаменитого художника Луки Синьорелли, его влияние отразилось в произведениях Мелоццо да Форли, отца Рафаэля, Джованни Санти, и других умбрийских мастеров, включая юного Рафаэля Санти.

Так случилось с Пьеро делла Франческа из Борго а Сан-Сеполькро. Он считается редким мастером в преодолении трудностей правильных тел, в арифметике и геометрии; вследствие наступившей в старости телесной слепоты и немощи он не мог выпустить в свет своих доблестных трудов и многих написанных им книг, которые хранятся еще на его родине в Борго. Тот, кто должен был изо всех сил стираться превознести славу Пьеро и его имя, так как научился у него всему тому, что знал, — тот, как нечестивец и злодей, пытался изничтожить имя Пьеро, своего наставника, и захватить для себя все почести, которые должны были принадлежать ему одному. То был брат Лука из Борго, опубликовавший под своим собственным именем все труды этого достойного старца, который кроме познаний, названных выше, был также превосходным живописцем» [14, с. 169 – 170].

Брат (фра) Лука из Борго — это и есть францисканский монах и странствующий учитель Лука Пачоли. В середине описания жизни Пьеро делла Франческа Вазари вновь обвинил его в плагиате.

«Пьеро, как сказано, очень усердно изучал искусство, много упражнялся в перспективе и обладал отличнейшим знанием Евклида, так что все лучшие повороты в изображении правильных тел он понимал лучше других геометров, и наилучшее разъяснение, которое существует на этот предмет, принадлежит его руке, так как мастер Лука из Борго, францисканец, который писал о геометрических правильных телах, был его учеником. И когда Пьеро состарился и умер, предварительно написав много книг, названный магистр Лука завладел ими для себя и отпечатал их как свои, ибо они перешли в его руки после смерти учителя. Пьеро часто делал модели из глины и покрывал их мягкими материями с бесконечными складками, чтобы срисовать их и пользоваться ими» [14, с. 175].

В 1475 году Пьеро делла Франческа написал картину «Мадонна со святыми» ("Montefeltro"), на которой изобразил монаха-мученика Доминиканского ордена Пьеро Мартира. Прототипом для него послужил Лука Пачоли. Он стоит вторым справа; у него на голове, на выбритой под нимб части голого черепа, видна кровь.

В примечаниях к этой биографии делается попытка оправдать Луку Пачоли, но довольно безуспешно.

«Лука Пачоли (1441 – 1514), знаменитый итальянский математик, автор «Summa di Aritmetica» (первое издание— Венеция, 1494) и «Divina proporzione» (первое издание — Венеция, 1509). Пьеро делла Франческа написал два трактата: «О живописной перспективе» («Depi i spectiva pingendi»), который был издан С. Winterberg'ом только в 1899 г. с немецким переводом по оригиналу, хранящемуся в Палатинской библиотеке в Парме, и «Трактат о пяти правильных телах», который никогда не был напечатан. Вопрос о плагиате дебатировали в 80-х годах [позо]прошлого столетия. С одной стороны, хорошо известен факт, что Пачоли во многих местах его «Summa di Aritmetica» с большой похвалой отзывается о Пьеро. С другой стороны, Jordan […] утверждал, что Пачоли присвоил себе латинское произведение Пьеро, опубликовав на итальянском языке в 1507 г. в Венеции «Libelliis de Vcorporibus regukn bus», нигде при этом не называя Пьеро. Крайности этих выводов пытался смягчить Winterberg […1882], указывая, что можно говорить лишь о совместной paботе обоих математиков, но никак не о плагиате. В недавнее время G. Mancini снова пытался доказать наличие плагиата […1916]» [14, с. 178].

Если бы обвинения касались только работ Пьеро делла Франческа, это было бы еще полбеды. Но Лука Пачоли замечен в воровстве идей и готовых текстов также и у других своих коллег и друзей (об этом ниже). Верно, что ему в большинстве случаев удавалось надежно скрыть следы своих преступлений, так что доказательства в плагиате носили только косвенный характер и часто выглядели натянутыми. Но древние римляне говорили: quod factum est, cum in obscuro sit, ex affectione cujusque capit interpretationem (когда не ясно, что содеяно, действие должно объясняться исходя из характера лица, которое его совершило). Его не раз уличали во лжи: falsus in uno, falsus in omnibus (ложное в одном, ложно во всем); qui semel malus, semper praesumiter esse malus in eodem genere (тот, кто однажды был дурным, всегда предполагается дурным в том же смысле слова). Эти юридические нормы Римского права нужно иметь в виду, когда занимаешься выяснением, что может принадлежать Луке Пачоли, а что Леонардо да Винчи в трактате «О божественной пропорции».

*
*   *

Дживелегов сообщает, что «можно считать очень вероятным, что Леонардо за это время [речь идет о годах 1482 – 1499] трижды принимался за составление чего-то вроде учебного пособия, но потом бросал, не доведя до конца. Начал составлять учебник элементарной геометрии, но в разгар работы до него дошла "Summa" Пачоли, и он увидел, что его учебник будет бесполезен: лучше, чем Пачоли, сделать он не мог, а хуже не стоило.

Одновременно — Леонардо ведь всегда одновременно был занят несколькими задачами — он собирал латинские слова и материалы для латинской грамматики: хотел составить латинскую грамматику на итальянском языке и латинско-итальянский словарь. Ни того, ни другого не существовало. Он отказался от этой мысли, когда в 1499 году в Венеции появился «Donatus italice», т. е. именно то, что было конечной целью кропотливого собирания материалов Леонардо» [12].

Можно смело предположить, что учебное пособие по евклидовой геометрии и создание латинско-итальянско словаря — две взаимосвязанные задачи. В Европе происходили тектонические сдвиги: народ отвернулся от латинизированной схоластики Аристотеля и повернулся к наглядно-образной философии Пифагора и Платона, геометрически выраженной Евклидом. Первое печатное издание «Элементов» («Начал») Евклида появилось в Венеции в 1482 году на латинском языке в переводе с арабского языка, выполненном Кампанусом (Компано) «еще в 1259 году и считавшийся долгие десятилетия классическим». Издатель Эргард Ратдольт выпустил их в свет под названием «Opus elementorum Euclidis Megarensis in geometriam artem, in id quoque Campani commentationes». «В 1486 и 1491 годах вышли повторные издания этого перевода. Однако в 1505 году в Венеции издается новый перевод, выполненный с греческого подлинника Бартоломео Замбсрутистом. В этом издании перевод Компано был подвергнут суровой критике» [15].

В 1508 году в Венеции выходят «Сочинения мегерянина Евклида, тончайшего философа и по справедливости первого из всех математиков, переведенные достойным внимания Компано. Сочинения эти по вине издателя были настолько искажены ошибками, что едва ли в них можно узнать Евклида. Пачоли, заслуженный теолог, сей высший и редчайший между математическими науками предмет по своему разумению исправил и издал». «Эта книга Пачоли, — пишет Соколов, — дошла до нас в одном-единственном экземпляре, который хранится в университете Болоньи. Суд потомства был не в пользу Пачоли. Считается, что в его переводе присутствует множество ошибок и темных мест» [15].

В библиотеке в Вольфенбюттеле хранится другой примечательный экземпляр «Начал» на латинском языке, на котором есть следующая надпись: «Эту книгу я купил в Венеции за один дукат в 1507 году. Альбрехт Дюрер» [13, c. 425]. Следовательно, немецкий художник приобрел экземпляр евклидовых «Начал», изданных не Лукой Пачоли. Свой трактат на немецком (не латинском!) языке с полным названием «Руководство по измерению с помощью циркуля и линейки в линиях и целых телах, составленное Альбрехтом Дюрером и напечатанное на пользу всем любящим знания с надлежащими рисунками в 1525 году» автор начал так: «Наимудрейший Эвклид заложил основы геометрии. Кто хорошо их понимает, тому совершенно не нужны эти написанные дальше вещи. Ибо они написаны только для юношей и для тех, кто не имеет хорошего учителя» [13, c. 119].

В 1528 году Дюрер издал другое сочинение на немецком языке под полным названием «Здесь заключены четыре книги о пропорциях человеческого тела, найденных и описанных Альбрехтом Дюрером из Нюрнберга на пользу всем любящим таковую науку». Начал он его словами: «Если я намереваюсь сделать изображение человека, то прежде всего я поступаю таким образом: я беру линейку длиннее, чем фигура, и провожу на ней прямую линию такой длины, какой должна быть изображенная фигура...» [13, c. 222].

О Дюрере и его упомянутых трактатах поговорим позже, но уже сейчас необходимо знать, что у этого художника всегда под рукой лежали циркуль и линейка. Он пользовался гармонической системой пропорций (1/2, 1/3, 1/4 и т.д.), которые откладывал по методике, изложенной Евклидом. Радзюкевич однажды написал: «Я уверен в обратном — шедевры архитектуры и искусства следует воспринимать и познавать, НЕ прибегая к помощи циркуля и калькулятора. Иначе мы превратимся в бухгалтеров. Убежден, что эти предвзятые вычисления НЕ способствуют развитию ГАРМОНИИ внутренней» (обсуждение статьи [1] от 20.08.2006).

Такое восприятие шедевров изобразительного искусства нужно отнести к субъективному видению того, кто это написал. Наверное, можно создавать шедевры и «на глазок», но при этом хорошо бы помнить, как великие мастера эпохи Возрождения, опираясь на объективную науку, т.е. на вычисления и геометрию Евклида, мучительно искали пропорции для идеального человека. Я нахожу вышепроцитированные слова Стахова абсолюно верными: «В эпоху Возрождения продолжаются поиски совершенной пропорции. В работах Леонардо да Винчи и Дюрера учение о пропорциях сводится к поискам идеальной меры человеческого тела ("Витрувийский человек" Леонардо да Винчи)».

Каждый шел своим путем: Леонардо и Дюрер, в конце концов, отказались от поиска теоретического абсолюта и признали прекрасным то, что создала природа. Для них «естественность» стала синонимом «гармоничности» и даже «божественности». Но, наверняка, были и такие, кто увлекся «божественной пропорцией» в понимании Луки Пачоли. Главное, что законы перспективного построения, изложенные в трактатах Леона Баттиста Альберти и Пьеро делла Франческа (учителя Луки Пачоли), основывались на знаниях геометрии Евклида.

Его «Начала» нужны были художникам, скульпторам и архитекторам как воздух. Вот почему Леонардо да Винчи хотел написать учебное пособие по основам геометрии Евклида не на языке схоластов, которого не знал простой народ, а на родном, итальянском языке. Теперь представьте себе счастливые глаза художника, узнающего, что в Милан, город в котором он тогда жил, приезжает прославленный математик. Естественно, он стал усердно посещать его лекции, быстро сдружился с ним, рассказал ему о своих планах и поделился уже собранными материалами. Это было легко сделать, поскольку Лука Пачоли чисто внешне был человеком приветливым и обаятельным.

*
*   *

Леонардо да Винчи и Лука Пачоли действительно дружно работали над книгой, посвященной обсуждаемой здесь теме. В поддержку позиции Стахова обратимся к другому специалисту, М.А. Гуковскому, написавшему книгу под тем же названием, что и Зубов. Процитирую из нее отрывок из главы «"Конь" и "Тайная вечеря"»: «В 1496 г. Лодовико Моро пригласил Луку Пачоли профессором в Павийский университет, и математик, соблазненный высоким гонораром, согласился.

Леонардо, как раз в это время с увлечением занимавшийся математикой и жаждавший пополнить свое не слишком глубокое теоретическое образование, немедленно по приезде Пачоли познакомился с ним. Знакомство это скоро перешло в тесное сотрудничество и даже (первый и последний раз в жизни скептического художника!) в дружбу. Пачоли работал по прибытии в Милан над своим "Трактатом о божественной пропорции" и сразу привлек к этой работе Леонардо.

В одной из своих записных книжек да Винчи объяснил на основе геометрического чертежа принцип действия современного фотоаппарата или, как говорили раньше, камеры обскура (camera obscura или, как у да Винчи, oculus artificialis). Этот принцип, изложенный в «Началах» Евклида, основывается на сохранении пропорций отрезков a-b-c-d-e и k-i-h-g-f; здесь s-t — экран, на который проецируется изображение, m-n — крохотное отверстие в камере q-r-o-p.

Леонардо сделал несколько геометрических рисунков, свидетельствующих о его интересе к геометрии; здесь показан один из них.

Из этого рисунка понятно, что Леонардо изучал математические пропорции по Евклиду; его рисунок Ms. K (IFP), K2, c. 28.

Возможно, что самая идея написать специальное сочинение о законах пропорциональности, о том "правиле золотого деления", которому подчиняются все земные предметы, претендующие на красоту, принадлежала Леонардо, уже давно занимавшемуся проблемой пропорций человеческого тела, склонному во всем находить законы пропорции. Несомненно (это подтверждено и самим Пачоли), что в подборе материалов для этого сочинения и в их обработке Леонардо принимал непосредственное участие; он же выполнил эскизы иллюстраций для книги.

"Трактат о божественной пропорции", напечатанный в 1509 г. и снабженный заглавными буквами, начинающими главы настоящей книги (весьма вероятно нарисованными самим Леонардо, дороги которого и Пачоли к этому времени уже давно разошлись) — одно из наиболее характерных и любопытных научных произведений Возрождения. В нем находит отражение то стремление подвести все сущее под небольшое количество математически формулируемых законов, тот наивный математизм и механицизм, которым проникнута вся культура Возрождения.

Сотрудничество Леонардо с Пачоли, тянувшееся с 1494 по 1500 г., было плодотворно и полезно для обоих. Мало знакомый с реальной жизнью, воспитанный на схоластических абстракциях, францисканец при помощи Леонардо начал связывать свои математические изыскания с практикой; научные работы художника, постепенно открывавшего другу тайны своих тетрадей, должны были представлять для ученого немалый интерес. С другой стороны, Пачоли давал Леонардо ряд ценных математических указаний, пополнявших недостаточные и несистематические знания винчианца.

В предисловии к "Трактату о божественной пропорции" Пачоли восхваляет Леонардо, своего друга и сотрудника, как одного из "мудрейших архитекторов и инженеров и упорнейших изобретателей разных новшеств", живущих в Милане. Пачоли с большой похвалой говорит о "Коне" и о "Тайной вечере" и заканчивает так: "Не довольствуясь этим, он (Леонардо.— М. Г.) принялся за неоценимое сочинение о местном движении, об ударе, весе и всех силах, то есть приобретаемых весах, причем принялся он за эту работу после того, как закончил весьма старательно достойнейшую книгу о живописи и человеческих движениях, и надеется и эту работу надлежащим образом довести до конца".

В этом несколько неловком, но искреннем восхвалении сквозит восхищение перед гениальной разносторонностью, глубиной и оригинальностью творчества Леонардо, которое Пачоли, лучше чем кто-либо из современников, смог узнать во всех его проявлениях. Упоминаемая Пачоли "Книга о живописи" Леонардо до нас не дошла, но мы можем составить себе довольно полное представление о ее построении и содержании по рассыпанным в большом количестве на листах его тетрадей замечаниям на эту тему, которые, как мы видели, он начал делать уже давно. Из этих записей после его смерти одним из его учеников, скорее всего Франческо Мельци, был составлен "Трактат о живописи", точно передающий систему взглядов Леонардо» [10].

Таким образом, утверждение Стахова о том, что трактат Пачоли «О божественной пропорции» писался «под непосредственным влиянием Леонардо» имеет определенные основания. Вместе с тем, утверждение Радзюкевича: «Никто, ни один художник или архитектор эпохи Возрождения или античности ни разу не упомянул о золотой пропорции и даже не намекнул на ее существование» должно приобрести не столь категоричную модальность, которую вложил в него автор.

Неправедная жизнь Луки Пачоли

В адрес Луки Пачоли раздавалась критика, будто свои сочинения он составлял из чужих трактатов. Так, Гуковский сообщает нам, что его книга «Сумма арифметики, геометрии, пропорции и пропорциональности», «во многом была простой компиляцией и содержала ряд ошибок» [10]. Этот странствующий из города в город учитель, «францисканский монах, поклонник античности и не менее страстный любитель точных наук» откуда-то узнает о тонкостях ведения бухгалтерского учета, о котором мог знать только человек, целиком посвятивший себя сделкам купли-продажи. Следовательно, «отцом бухгалтерии», как его часто называют, он сделался благодаря какому-то настоящему бухгалтеру.

В связи с обвинениями в плагиате авторы, пишущие о Пачоли, разделились на два противоборствующих лагеря — тех, кто поддерживал эти обвинения, и тех, кто пытался обелить его имя. Гастев, например, сначала закрывал глаза на воровство идей у его наставника: «И напрасно утверждение Вазари, будто Лука бессовестно обобрал своего земляка и преподавателя Пьеро делла Франческа, живописца, опытнейшего математика и знатока перспективы, хотя бы важнейшие части написанных на народном языке трактатов Луки Пачоли суть перевод из латинских сочинений этого Пьеро, его наставника. Существенное достоинство ученых рассуждений Луки Пачоли, когда он бывает самостоятелен, хорошо видно там, где он сводит различные вещи и находит аналогию, если даже другой человек ничего подобного не замечает. Таким образом, францисканца в его рассуждениях следует решительно уподобить птице, не смущаясь расстоянием прыгающей с ветки на ветку в поисках корма» [11].

Гастев приводит те самые аналогии, которые нашел Пачоли самостоятельно. Автор трактата «О божественной пропорции», заметил, например, что число свойств «божественной пропорции» в точности равно числу лиц, присутствовавших на трапезе «Тайная вечеря» одноименной картины Леонардо, «а когда он рассматривает пять соответствий пропорции с Богом, то в четырех находит аналогию с небесными добродетелями, которых столько же. Отсюда Пачоли приходит к простым телам и далее, к четырем элементам: земле, воздуху, воде и огню» [11].

Но позже Гастев замечает слишком явные математические спекуляции Пачоли и начинает иронизировать: «Но как некоторые верующие: чем усерднее отбивают поклоны и крестятся, тем чаще нарушают заповеди божьи вне храма, когда маэстро приступает к чистой теории, он не связывает себя и малейшим правдоподобием. Так, разбираясь с корнями, умножению которых он обучал Леонардо, Лука Пачоли приводит задачу о путешествиях: торговец столько раз путешествовал, сколько у него вначале было дукатов; спрашивается, сколько он совершил путешествий, если при каждой отлучке количество дукатов удваивалось и, в конце концов, стало их 90. Ответ поражает странностью: число путешествий оказывается равным

1 + sqrt ( 4 + ¼ ).

Здесь sqrt — квадратный корень; в другой похожей задаче ответ выглядит следующим образом:

3 ²⁴⁷³³ / 63308 + sqrt ( 7 ^164348177 / 4007902864 )»     [11].

Даже школьник сообразит, что в последнем случае степени с основанием 3 и особенно 7 дают сумасшедшие величины, а главное, не понятно, как было получено это абсурдное выражение. В этой связи в качестве примера можно привести американского профессора Андрея Линде из Стэндфордского университета, предложившего уже в наши дни инфляционную модель вселенной. Он считает, что наша вселенная содержит 10⁸⁷ элементарных частиц и весит 10⁵⁰ тонн. Эти числа меньше, чем у Пачоли, но тоже нереальные и непонятно откуда взятые.

Уверенно можно сказать: тот, кто пишет подобные выражения, хочет произвести впечатление на несведущих людей, будто он большой специалист в области математики, хотя в действительности таковым не является. На удочку хитреца поймался и наш критик. «Если бы Леонардо точно следовал содержанию текста Луки Пачоли, — пишет Радзюкевич, — то ему пришлось бы строить правильный пятиугольник с помощью приведенной в трактате формулы "золотого сечения". В переводе на современные математические символы, эти формулы имеют следующий вид:

,         .

Предположение о том, что Леонардо да Винчи мог практически оперировать такими формулами и, в частности, строить с их помощью форму додекаэдра, выглядит просто невероятным» [4].

В другой своей статье Радзюкевич пишет: «В трактате "О божественной пропорции", оформленном Леонардо да Винчи, Лука Пачоли дает приблизительные математические формулы пропорции "золотого сечения". В переводе на современные математические символы эти формулы таковы» [1] и далее приводятся те же два выражения.

Не «приблизительные», а совершенно точные формулы числа Ф = 1,618… Похоже, Лука действительно морочил людям голову, подобно Андрею Линде. Наиболее простое выражение для Ф:

он шифровал тождественными выражениями, записанными более громоздко. Чтобы это понять, нужно обратить внимание на два квадратных корня, которые могут быть представлены через один квадратный корень из пяти:

        и         .

Таким образом, можно построить бесконечное количество представлений одного и того же иррационального числа Ф. Так, например, на базе двух корней:

        и         ,

получаются еще два тождественных представления числа Ф:

        и         .

Для проверки правильности найденных выражений составьте равенство, например, такое:

  =   ,

выделите корень из пяти в правой части, перемножьте числители и знаменатели крест на крест и сократите однородные члены. За основу числовых махинаций могут быть взяты другие тождественные выражения для числа Ф, в частности, такое:

.

Как раз эти элементарные манипуляции с формулами доказывают спекулятивно-показушную сущность характера Луки Пачоли.

Разумеется, он отлично знал традиционную формулу, но скрывал ее, предпочитая писать вместо нее более сложные выражения. В то время многие утаивали свои особо значимые результаты — дурное наследство алхимиков и прочих мистиков. Впрочем, так поступали и софисты, в частности, Евклид. В своих «Началах» он дал сложное, специально выдуманное доказательство теоремы Пифагора, хотя до него были известны несколько достаточно тривиальных доказательств (см. п. Математика древних ). Точно так же поступали и средневековые схоласты, и до сих пор нередко поступают современные преподаватели. Чтобы набить себе цену, они нарочито усложняют преподносимый учащимся материал, говорят загадками, парадоксальным или темным языком, получая от этого только им ведомое удовольствие.

С античных времен известно три элементарных способа нахождения золотой пропорции, которые были известны, по-видимому, Луке Пачоли и Леонардо да Винчи.

1) Способ построения через равносторонний треугольник: опешите вокруг равностороннего треугольника окружность; проведите через середины двух сторон треугольника прямую AB и продолжите ее до точки C, лежащий на окружности; отношение AB / BC = Ф.
2) Способ построения через квадрат: впишите в полуокружность квадрат со стороной AB; тогда отношение этой стороны AB к отрезку BC на диаметре окружности даст золотую пропорцию, т.е. AB / BC = Ф.
3) Способ построения с помощью пентагона: опешите вокруг пентагона окружность; тогда три линии, соединяющие не смежные вершины пентагона, дадут отрезки, находящиеся в золотой пропорции AB / BC = Ф.

Существуют и другие приемы построения золотого сечения с помощью угольника и циркуля, например, те, что показаны следующими двумя чертежами.

Кажется, этих способов вполне достаточно. Но одному гармонисту-золотоискателю — сейчас не могу вспомнить его имени — показалось этого мало. Он построил золотое сечение сложным способом, который показан на следующем рисунке (красным пунктиром прочерчены вспомогательные линии, сплошная синяя линия LM сечется точкой K в отношении LK / KM = Ф; непонятно, зачем надо было описывать внешнюю окружность вокруг квадрата ABCD). Некоторые только тем и занимаются, что выдумывают всё новые и новые способы; занятие, наверное, интересное, но абсолютно бесполезное.

Открытие новых способов построения золотого сечения превратилось в один из видов спортивного состязания. На марке, ниже цены 0,99 € показан оригинальный способ построения отрезка АК = 1,618…

Сомнения Радзюкевича, высказанные в статье [4] относительно того, что в представлении Пачоли золотая пропорция приобретала невероятно сложный вид, иллюзорны. Глядя на формулы из трактата «О божественной пропорции», критик пишет: «Невозможно даже представить себе, как мог бы зодчий рассчитывать смету и задавать строителям размеры элементов сооружений с помощью таких формул. Неудивительно поэтому, что в трактатах теоретиков эпохи Возрождения, в том числе и в трактатах и записках Леонардо да Винчи, пропорция "золотого сечения" не нашла никакого отражения» [1].

Маленькая бронзовая монета 4 – 3 века до н.э. с изображением пифагорейской пентаграммы.

Для архитекторов и строителей эпохи Возрождения в этом деле ничего не изменилось по сравнению с эпохой Античности, когда жил Евклид. Разделить измерительную линейку или веревку в соответствии с числом Ф не представляло большого труда — ни для античных мастеров, ни для Леонардо да Винчи. Между тем, две нарочито усложненных формулы золотого сечения, взятые из трактата «О божественной пропорции», доказывают не только спекулятивный дух автора, но и тот непреложный факт, что люди эпохи Возрождения таки владели золотым сечением, прятали его друг от друга, всячески обыгрывая его исходную формулу. А ведь именно это является предметом спора между директором Института Золотого Сечения и доцентом кафедры «Компьютерные технологии проектирования» Новосибирской государственной архитектурно-художественной академии.

*
*   *

Еще большую беспринципность, чем Гастев, продемонстрировал Соколов, написавший послесловие к «Трактату о счетах и записях» [15]. Он приводит разоблачительные факты плагиата и наряду с ними выдвигает несколько худосочных аргументов, оправдывающих поведение плагиатора, будучи уверенным, что «Лука Пачоли: человек и мыслитель» (название его статьи) в смысле «великий человек» и «великий мыслитель».

«Еще при жизни Л. Пачоли, — пишет Соколов, — некто Коро назвал его сочинения кучей золы, в которой скрыты крупицы золота». В 1523 году выходит второе издание «Суммы». «Однако очень скоро Дж. Кардано (1501 – 1576) назовет Л. Пачоли компилятором. Эта оценка сохранится надолго. В наши дни Я. Кубеша с грустью писал, что «специалисты-математики не слишком высоко оценивают его (Пачоли. — Я. С.) печатные труды, поскольку они не содержат каких-либо новых идей» [Kubesa]. Л. Ольшки, А.П. Юшкевич считали Пачоли популяризатором, ... , Н. Бурбаки не удостаивает его упоминанием» [15, с. 221 – 222]. Прежде чем об этом мы заговорим подробно, давайте ознакомимся, хотя бы кратко с жизненным путем, проделанным другом Леонардо да Винчи.

Из жизнеописания Вазари нам известно, что Пачоли безуспешно обучался живописанию у художника Пьеро делла Франческа, который, однако, был сильно увлечен пифагорейско-платоновской философией и евклидовой геометрией. Ученик не только перенял эти знания от него, но и выгодно распорядился ими в отличие от учителя. Франческа познакомил его со знаменитым архитектором и ученым Леоном Баттиста Альберти (1404 – 1472), который устроил 19-летнего молодого человека в дом богатого венецианского купца, Антонио де Ромпиази (или, Ромпиачи?). Живя в доме купца и обучая его трех сыновей, Пачоли учится сам, посещая лекции математика Доменико Брагадино.

Предполагают, что он пользовался доверием у Ромпиази, плавал вместе с ним «на кораблях, перевозящих товары», помогал вести бухгалтерский учет, который в то время причислялся к математическим наукам. В 1470 году он составил что-то наподобие учебного пособия по «коммерческой арифметике», которое до нас не дошло. В том же году он покинул дом купца и поселился в доме Альберти, который находился на территории Ватикана.

Здесь он проявляет чудеса прозорливости, когда знакомится с нужными людьми. Пачоли заводит дружбу с двумя важными священнослужителями, которые в будущем станут папами под именами Сикста IV и Юлия II, племянник Сикста IV. Папа Сикст IV, понтификат которого начался в 1471 году, до этого носил имя Франческо делла Ровере и занимал должность генерала Францисканского ордена. Как только он становится папой, 27-летний Пачоли становится монахом этого ордена и уезжает к себе на родину, в Борго Сан-Сеполькро.

Лука Пачоли с учеником (возможно, Гвидобальдо ди Монтефельтро?); картина хранится в Национальном музее Неаполя. Судя по манере письма, предполагают, что картину нарисовал в 1495 году венецианский художник Якопо де Барбари (Jacopo de' Barbari). Однако существует версия, что ее нарисовал совершенно другой человек, а именно, племянник Пачоли. Мне кажется, что вторым человеком здесь является сам художник, поскольку он смотрит на нас, как бывает в случае рисования автопортрета с помощью зеркала. Не показана также правая рука, которой художник рисовал. Если бы это был ученик, он должен был смотреть на чертеж, лежащий на столе.

В [17, с. 287] утверждается, что рядом с Пачоли стоит молодой герцог Урбино. Как бы там ни было, мы отчетливо видим, что Пачоли хотел предстать перед потомками в образе ученого-монаха, который подарил миру «божественную пропорцию». Поэтому юбилейная надпись на марке 500 лет «Сумме арифметики, геометрической пропорции и пропорциональности» здесь не совсем уместна. Эта картина больше подходит к выходу в свет трактата «О божественной пропорции» (1509). На марке, выпущенной в 1994 году, отпечатан малоизвестный (черновой?) вариант этой картины, который существенно отличается от окончательного варианта.

На черновом варианте допущена ошибка: доска с чертежом оказалась позади Пачоли, так что он не может видеть чертеж, который является важным элементом сюжета картины. Известно, что он внес некоторое добавление в теорему Евклида, касающуюся равностороннего треугольника, вписанного в окружность. Правой рукой монах показывает на прочерченный им отрезок, а левой указывает на соответствующее место в тексте «Начал» Евклида. Кроме того, на окончательном варианте картины мы видим стеклянный ромбокубооктаэдр, подвешенный к потолку и наполовину наполненный водой. Вода нужна для изучения преломления и отражения света в многогранниках. Ромбокубооктаэдр обладает особыми оптическими свойствами, которые изучались в реалистической школе (della scuola di Rialto) и, вероятно, в Академии Леонардо да Винчи (об этом ниже).

В правом нижнем углу картины мы видим также додекаэдр. Не исключено, что оба правильных многогранника изготовил Леонардо да Винчи. Картина рисовалось, когда Пачоли вместе с Леонардо работал над трактатом «О божественной пропорции», так что полотно прямо-таки пропиталось духом «божественной гармонии». А вот армиллярная сфера оказалась лишней (ее мы видим на первом варианте), поскольку отец бухгалтерии не интересовался небесной механикой. Обе картины демонстрируют нам самовлюбленного Пачоли, позирующего перед потомками. Скромность Леонардо да Винчи всегда бы удержала его от столь откровенной похвальбы и позерства.

В 1477 году фра Лука из Борго — так звали монаха Пачоли — становится профессором университета Перуджи, где начинает читать лекции по математике и пишет два учебных пособия — «Алгебра» и «Пять законов Платона» (о Платоновых телах). Позже содержание этих пособий войдет в «Сумму». В конце 1480 года он прекращает чтение лекций в университете и посвящает себя орденским делам, которые никогда не прерывал. Он живет в Заре, но часто выезжает во Флоренцию и другие города Италии по поручениям генерала ордена францисканцев. Перед рождеством 1487 года Лука Пачоли вновь заступает на математическую кафедру университета Перуджи. В это время он составляет детальный план «Суммы» всех математических знаний, собирает и обрабатывает материал для нее, но в апреле следующего года он едет уже в Рим для работы в аппарате тамошнего епископа.

Здесь он тесно сотрудничает со своим старым знакомым, кардиналом Джулиано делла Ровере (1441 – 1513), будущим папой Юлием II. В период с 1490 по 1493 год он живет в Неаполе, но часто выезжает по делам в Падуе и другие города, в частности, в свой родной город, Борго Сан-Сеполькро на похороны своего первого учителя, Пьеро делла Франческа. Вазари, посвященный в тонкости его биографии, утверждает, что он выкрал у своего учителя неопубликованные рукописи. Этому есть весомые доказательства, которые, однако, редко приводятся в официальных биографиях. В них лишь говорится, что одной из главных причин разъездов по стране становится чтение лекций; он превращается в «странствующего профессора математики» — таков его официальный статус в монашеском ордене святого Франциска.

Наконец, 10 ноября 1494 года в венецианской типографии Паганино Паганини на деньги мецената Марко ди Сануто выходит его «Summa de Arithmetica, Geometria, proportioni et Proportionalita» — «Сумма арифметики, геометрии, учения о пропорциях и отношениях». Над этой книгой в общей сложности с небольшими перерывами он проработал три десятилетия. Написана она на итальянском языке, точнее, на помеси итальянского языка с латинским. По-видимому, это связано с теми тектоническими сдвигами общественного сознания, о которых рассказывалось выше. Но сюда примешивалось и нечто личное.

«Существенно, — пишет Соколов, — что книга Л. Пачоли написана не на латинском языке, на котором тогда делалась наука, а на вольгаре, насыщенном латинскими выражениями и формами. Почему Пачоли поступил так? Л. Ольшки видел в этом "признание ученым того факта, что латынь непригодна для научных целей. Подобные высказывания мы находим еще до Пачоли (Альберти, Гиберти)". Итак, если верить Л. Ольшки, а его поддерживал и Я. Кубеша, то Пачоли выступает как один из создателей народного и всем доступного языка науки. Из уважения к автору здесь забывают отметить, что Л. Пачоли, будучи самоучкой в математике — он учился в мастерской художника, а церковнослужителем стал, когда ему было уже больше тридцати лет, просто не владел достаточно свободно латинским языком. Поэтому неизмеримо ближе к истине были первый биограф Луки Пачоли Бернардо Бальди (1553 – 1617) и историк математики М. Кантор, которые называют Пачоли за его язык и стиль варваром» [15, с. 205 – 206].

Согласно первоначальному плану, «Сумма» делилась на пять частей:

1) Арифметика и алгебра.
2) Различные вопросы, касающиеся торговли (включая векселя и меновые сделки).
3) Ведение бухгалтерского учета и счетов.
4) Весы, меры и проценты.
5) Геометрия.

Но в окончательном варианте она делилась на две неравные части, каждая из которых состояли из отделов, разделенных на отдельные трактаты. Первая часть состоит из девяти отделов; первые восемь посвящены арифметике и алгебре, а девятый — «вопросам применения математики в коммерческом деле. В последний отдел входит двенадцать трактатов:

I — о товарищах,
II об арендах,
III — о менах и меновых сделках,
IV — о векселях и вексельных сделках,
V — о процентных вычислениях...
XI — о счетах и записях,
XII — о мерах, весах и монетах, о торговых обычаях и местах, с которыми Италия находится в торговых сношениях» [15, с. 202 – 203].

Такова структура «Суммы», в которой одиннадцатый «Трактат о счетах и записях» считается наиболее интересным. Из всех многочисленных подразделов этого объемистого фолианта он единственный удостоился перевода на русский язык. Однако…

*
*   *

«С точки зрения практики учета, — пишет Соколов, — книга Л. Пачоли устарела еще до того, как была напечатана. Это хорошо и убедительно показано Р. де Рувером, Н.С. Помазковым [1940] и В. И. Рутенбургом [1965].

Практика учета в Северной Италии к концу XV в. была шире и глубже, чем описал ее Лука Пачоли, и, пожалуй, можно сказать, что для итальянских бухгалтеров — современников Пачоли его книга в части практических предложений была весьма элементарна. В своем классическом труде он не отразил многих ценных практических достижений. Это свидетельствует о том, что Пачоли в основном, очевидно, опирался на торговые книги практического счетоводства Ромпиази.

Отсюда можно сделать вывод, что Пачоли не был знаком с учетом как профессионал. Только этим можно объяснить некоторую ограниченность труда; в нем не нашли места такие важные и уже встречавшиеся в практике того времени приемы и методы, как:

1) учет затрат в промышленности;
2) ведение параллельных и дополнительных книг;
3) ведение счетов лоро и ностро;
4) применение баланса в аналитических целях, так как уже тогда баланс составлялся не только для закрытия книг и выверки записей, а служил орудием контроля и управления;
5) правила проверки и основы ревизии баланса;
6) порядок резервирования хозяйственных средств и распределения результатов по смежным периодам;
7) методика расчетов, связанных с распределением прибыли;
8) подтверждение отчетных данных инвентаризационными ведомостями.

Существенным недостатком концепции Пачоли, единодушно отмечаемым всеми исследователями, кроме Дюпона, было отождествление домашнего (личного) имущества купца с имуществом предприятия. Трактат написан на языке, представляющем собой смесь латинского и итальянского с явным преобладанием последнего, что делало его сложным для чтения и понимания. Наконец, изложение в трактате очень небрежное, содержит много противоречий.

Достаточно сказать, что при описании правил заполнения инвентаря игнорируются цены (глава 3), когда же автор переходит к изложению правил открытия счетов в Главной книге, то предполагается наличие цен (глава 12). Столь же противоречивы высказывания и о сроках сальдирования счетов Главной книги, о классификации расчетов (сравни главы 9 и 19). Остается неясной позиция Пачоли относительно принципов оценки материальных ценностей (см. главы 12, 18 и 20)» [15, с. 224].

Мало того, что данный Трактат сам по себе страдает существенными изъянами, видный итальянский бухгалтер, Фабио Беста, в 1891 году серьезно усомнился в авторстве Пачоли. В самом деле, «Вся "Summa" написана на тосканском, родном для Л. Пачоли, диалекте, а Трактат XI — на венецианском. … Беста полагал, что просто нельзя написать такое фундаментальное произведение, как Трактат, не использовав литературу по данному вопросу, а использовать — значило вставить в свою книгу текст предшественника. Следовательно, до Трактата уже была книга по двойной бухгалтерии. Беста пишет "... в Венеции имелось и было популярным в школах более стройное и значительно более точное произведение, чем его малопохвальная переделка", которая свелась к тому, что Пачоли:

1) дал книге пышное наукообразное и небухгалтерское название,
2) исправил даты записи фактов хозяйственной жизни и
3) дополнил содержание первой главы» [15, с. 231].

В другом месте читаем: «Не меньшие сложности возникают и с "Summa". В. Альфиери указал, что Трактат XII из "Summa" ранее публиковался во Флоренции (1481) и автором этого трактата был Джордже ди Лоренцо Кьярини [Alfieri, с. 110]. Р. Браун, изучая одну из первых английских книг по бухгалтерскому учету, принадлежавшую Хью Олдкаслу (1543), и сравнивая эту книгу с Трактатом, пришел к выводу, что первая списана со второй. Тщательно сверив обе книги, Беста писал: "Олдкасл перевел не «Трактат о счетах и записях", а более старинную венецианскую рукопись» [Besta, т. III, с. 374]. "...и Пачоли, и Олдкасл прибегли к фальши лишь для того, чтобы зарекомендовать себя, — один верным воспроизводителем, а другой — верным переводчиком одного и того же произведения, принадлежащего другому лицу; их ложь лишь в том, что они умолчали об источнике" [Besta, т. III, с. 374]. … Р. де Рувер, Р. Олотт и Э. Стевелинк продолжали утверждать, что Пачоли только перередактировал уже готовый не им составленный бухгалтерский текст. Два последних автора, повторяя прием Бесты, намекают на возможного автора этого текста — ди Бьянчи [Haulotte, с. 56]» [15, с. 234 – 235].

Соколов высказал сомнение относительно плагиата, но его аргументы столь ничтожны, что их не приходится принимать в расчет. Он пишет:

«1) даже если предположить, что Пачоли был человеком нерелигиозным и не стремился к вечному блаженству, не боялся "геенны огненной", то, тем не менее, посвящая свою книгу П. Содерини, гонфалоньеру Флоренции, он рисковал поплатиться за обман весьма суровыми карами не на том ирреальном свете, а на этом, вполне реальном;

2) Пачоли не раз ссылался на П. делла Франческа, своего учителя, так же как и в Трактате он не пишет, что создал, изобрел, сконструировал двойную запись, а что он "только будет держаться венецианского способа";

3) знаменитый математик, историк науки, земляк Пачоли — Бернардино Бальди; (1553 – 1617) в своей книге "Хроника математики"; (1589) называет Пачоли "величайшим гением своей эпохи"; и у него, так близко стоявшего к нашему автору, нет даже тени сомнения в неоригинальности работы;

4) Пачоли был широко признанным математиком. Он читал лекции, консультировал не только студентов, но и таких людей, как Леонардо да Винчи, решал практические задачи и уже в силу этого не мог быть обманщиком, ибо математика и иностранные языки — это, по выражению Л. Толстого, единственные области человеческой деятельности, где человек не может лгать» [15, с. 233].

По первому пункту: посвящение высокопоставленному лицу дает дополнительный уровень защиты; оно отводит изготовителя фальшивки от подозрений. По второму: плагиатор больше жеманничает, когда признается, что, вообще-то, идея ему не принадлежит; он только обобщил народный опыт. Третий пункт говорит нам о том, что «земляк», назвав Пачоли «величайшим гением своей эпохи», был либо не проницательным и поверхностным исследователем, либо не искренним и лицемерным человеком. Четвертый пункт вкупе с предыдущими тремя свидетельствует о наивности и доверчивости Соколова, который готов поверить любому авантюристу, лишь бы он был широко известен.

Защитник мошенника по ходу критики и обвинений его в плагиате привел еще несколько оправдательных мнений зарубежных авторов, которые, однако, не отменяют приведенные выше аргументы. Соколов не учитывает также авантюристическую натуру «отца-основателя бухгалтерии», хотя сам привел пример его аморального поведения. Речь идет об обвинении, выдвинутом двумя монахами францисканского ордена.

В их «доносе» — можно и так сказать — генералу ордена говорилось, что «этот маэстро Лука неподходящий человек, чтобы управлять другими, и у него нет таких навыков, чтобы он подвергал наказанию или исправлял других, так как сам он, соответственно тому, что мы видим ежедневно, является человеком, которого надо исправлять, и по этой причине вышеупомянутый монастырь терпит ущерб при собирании подаяний и других вещей, которые перечислять было бы слишком долго» [15, с. 215].

Этому делу был дан ход. В чем именно состояло обвинение, в «доносе» не говорилось, так как суть его должна была передаваться подателем устно. Но обвинения были серьезными, так что Пачоли не смог «отмыться» до самой своей смерти. Частично дело вращалось вокруг денег: «Папа Юлий II, давнишний знакомец Пачоли, буллой от 28 апреля 1508 года разрешил монахам нищенствующих орденов завещать из своего имущества до 300 широких золотых дукатов. Судя по завещанию, составленному 21 ноября 1511 года, у Пачоли было личное состояние на большую сумму» [15, с. 220].

Кроме того, Соколов привел текст из письма Пачоли от 1 января 1511 года, который, однако, трудно понять. Может быть, Вы, дорогой читатель поймете. В нем говорилось: «Я, маэстро Лука Пачоли из Борго Сан-Сеполькро, Ордена миноритов, узнал, что наш светлейший ... отец... из Лиссабона написал некие письма в монастыри и об одном в особенности, и в результате этого брат Кристофано и я были вызваны сюда капитаном и комиссионером Антонио де Дупие Нази, чтобы услышать решения, принятые в связи с письмами: поэтому в этот день я поискал его (фра Кристофано) и мне его поискали, пока, наконец, не нашли. Мы встретились, и, заметьте, я пообещал ему и каждому из прочих членов монастыря сделать все, что ранее упомянутый брат Гометрио потребует, прикажет, умолит меня сделать в исполнение этих писем, когда мы прибудем в Борго и когда я получу в свои руки ключи от монастыря. При условии, что отдача ключа будет согласована между ним и мною впридачу к упомянутому исполнению (писем), пусть каждое из наших разногласий между мною и монастырем будет доноситься до сведения почтенных господ Джакомо Венути, Николи Риджи и Вальдино Грациана и подобным же образом пусть и он ведет себя по отношению ко мне, как требуют упомянутые письма. И ему следует подписывать имя своей собственной рукой, как принято» [15, с. 218 – 219].

Сам стиль этого письма, а также расплывчатое содержание отрывков из писем 1512 и 1513 года говорят нам о скользком характере их автора. Тем не менее, в конце своей статьи Соколов написал: «Трактату исполнилось более 500 лет, и около 100 последних лет делались безуспешные, как мы видим, попытки поставить под сомнение авторство Пачоли. Из этой критики он вышел победителем» [15, с. 236].

После этого Соколов процитировал надпись на мемориальной доске: «Луке Пачоли, который был другом и советником Леонардо да Винчи и Леона Баттиста Альберти, который первым дал алгебре язык и структуру науки, который применил свое великое открытие к геометрии, изобрел двойную бухгалтерию и дал в математических трудах основы и неизменные нормы для последующих исследований. Население Сан-Сеполькро по почину исполнительного комитета общины, в исправление 370-летнего забвения, водрузило (эту доску) своему великому согражданину, 1878» [15, с. 237].

Нельзя дать объективной оценки, если опираться на текст мемориальной доски. Подобные приемы тоже воспринимаются не иначе как спекуляция. Лучше помнить заповедь: «Не верьте единожды солгавшему!» Лука Пачоли обманывал и не раз. Есть у всех мошенников что-то объединяющее их: я нахожу много общего в поведении Пачоли и Фрейда. В частности, Пачоли хвалил Пьеро делла Франческа и Леонардо да Винчи, а Фрейд — Йозефа Брейера и Эрнста Флейшля; и так бывает часто: обкрадывающий превозносит до небес свою жертву.

В «Истории математики» сообщается, что книгу «О божественной пропорции» Пачоли написал по просьбе Леонардо да Винчи [17, с. 286]. Она слагалась из трех частей: первая часть основывалась на XIV книге евклидовых «Начал», которую написал Гипсикла; вторая часть рассказывала о пропорциях человеческого тела (они выражались в целых числах, меньших 10); третья часть базировалась на книгах по зодчеству, написанных Витрувием. Ничего нового в его труде не было.

То же самое говорится в «Истории математики» и о другом его сочинении. «Задачи, решаемые в "Сумме" (1494), не выходят за пределы задач, решавшихся в "Книге абака" (1202) Леонардо Пизанского (Фибоначчи), за "Практической геометрией" (1220) которого следует и геометрическая часть "Суммы"». «Сын своего времени, Пачоли дает мистическое объяснение того, что совершенные числа оканчиваются лишь на 6 и 8 тем, что добрые и совершенные люди соблюдают установленный порядок. По самым разнообразным поводам Пачоли цитирует Библию» [17, с. 287].

В предыдущем подразделе говорилось, что Леонардо да Винчи был честен и трудолюбив, высоко чтил математику. В этом подразделе показано, что Лука Пачоли слишком много ловчил и математик был неважный. В лучшем случае, его можно назвать популяризатор науки, хотя он слишком часто прибегал к приемам, которые отнюдь не способствовали развитию рациональных знаний. Его показная и во многом фальшивая ученость заслоняла от публики настоящего автора или, во всяком случае, соавтора трактата «О божественной пропорции», которым был Леонардо да Винчи.

Основой для трактата послужили сделанные им 59 деревянных моделей, которые он построил, конечно, самостоятельно, без каких бы то ни было рекомендаций со стороны Пачоли. Помимо пяти Платоновых тел и тринадцати Арихимедовых (см. выше Таблицу многогранников), в трактат «О божественной пропорции» вошли звездчатые тела (типа звезды Кеплера), которые получаются не путем отсечения вершин, а путем присоединения их.

Зная творческую натуру Леонардо, можно допустить, что эти сложные конструкции появились на свет в результате геометрических фантазий мастера; во всяком случае, их вряд ли придумал монах. Мистика Пачоли и его религиозные откровения, а самое главное, очень неудобоваримая система математических обозначений, о которой рассказывается в [17], только затрудняли усвоение рационального материала, почерпнутого в основном из Евклида и других источников.

Указанные доводы ложатся тяжелым грузом на чашу весов Стахова, выступающего на стороне Леонардо, и она, в конце концов, начинает перевешивать чашу Радзюкевича, выступающего против итальянского мастера.

---

1. Радзюкевич А.В. Красивая сказка о «золотом сечении» // http://www.sibdesign.ru/ (2002) // «Академия Тринитаризма», М., Эл № 77-6567, публ.12981, 17.02.2006.
2. Радзюкевич А.В. Золотой блеск модулей Парфенона// «Архитектура», приложение к «Строительной газете» — 1989, № 14.
3. Радзюкевич А.В. Знал ли Леонардо да Винчи «код да Винчи»? (29.01.2008) http://www.a3d.ru/architecture/stat/213
4. Радзюкевич А.В. Глава из книги «Законы красоты — мифология или технология?» (06.02.2006) http://www.a3d.ru/architecture/stat/176
5. Радзюкевич А.В. Пропорционально-метрологические и масштабные особенности чертежей Андреа Палладио. http://www.archi.ru/lib/publication.html .
6. Стахов А.П. Гармония Мироздания и Золотое Сечение: древнейшая научная парадигма и ее роль в современной науке, математике и образовании. Часть 1 //«Академия Тринитаризма», М., Эл № 77-6567, публ.12840, 19.01.2006.
7. Стахов А.П. Гармония Мироздания и Золотое Сечение... Часть 2.
8. Стахов А.П. Интервью у него берёт Юрий Чёрный. "Наука и эзотерическая традиция" Выпуск 27 от 05.05.2006.
9. Зубов В.П. Леонардо да Винчи, — М.-Л.: Издательство АН СССР, 1962.
10. Гуковский М.А. Леонардо да Винчи. М., 1967. -180 С. Гл. "Конь" и "Тайная вечеря" // http://www.vinci.ru/gukov_1.html .
11. Гастев А.А. Леонардо да Винчи. - М.: Мол. Гвардия, 1982. - 400 с., Ил. - (Жизнь замечат. Людей. Сер. Биогр. Вып. 9 (627)). // http://www.vinci.ru/gastev65.html 12. Дживелегов А. Леонардо да Винчи Изд. 3-е М., Искусство, 1974. - 233 с. // http://www.vinci.ru/dj2_11.html .
13. Дюрер, Альбрехт. Трактаты. Дневники. Письма. — СПб: Азбука, 200. .
14. Вазари Дж. Жизнеописания наиболее знаменитых живописцев, ваятелей и зодчих / Пер с итал. Редакция и вступительная статья А. Дживелегова, А. Эфроса. — Ростов н/Д: «Феникс», 1998. — 544 с. // В этом издании опубликованы только 12 биографий наиболее известных личностей. В Интернете (http://painting.narod.ru) можно найти полное издание Вазари .
15. Пачоли, Лука. Трактат о счетах и записях / Перевод Э.Г. Вальденберга. Издание подготовил и написал послесловие Я. Соколов. — М.: Финансы и статистика, 1983 / Интернетовская версия (http://ek-lit.narod.ru/lukasod.htm) имеет несколько расширенный вариант послесловия Соколова "Лука Пачоли: Человек и мыслитель".
16. Брагина Л.М. Леонардо да Винчи и Лука Пачоли // http://www.vinci.ru/mk_09.html.
17. История математики с древнейших времен до начала XIX столетия (в 3-х томах). Под редакцией А.П. Юшкевича. Т.1. — М.: Наука, 1970.