
Конец науки
Акимов О.Е.
10. Критика Сергея Василенко
- В спор по истории ЗС вступает Василенко
- От теории РЗС к раковине Nautilus pompilius
- Всеобщая Гармония Мироздания по Василенко
- Как поссорились Сергей Леонидович с Алексеем Петровичем
В спор по истории ЗС вступает Василенко
Для тех, кто начал читать данную работу с этого места, рекомендуется прочесть хотя бы последний подраздел предыдущей страницы Белянин и Стахов: спор вокруг Евклида, чтобы войти в курс дела. Представленная там полемика касается сложной, запутанной, но важной темы осознания золотого сечения (ЗС) как математического и философского принципа организации гармоничных и прекрасных вещей физического и духовного мира. Основная статья В.С. Белянина [1], вызвавшая спор между ним и А.П. Стаховым, директором Института ЗС и главой Международного Клуба ЗС, затронула историческую тему: «Владел ли Платон кодом золотой пропорции?» На этот вопрос автор ответил отрицательно, оказавшись правым лишь частично. Он прав с точки зрения избранного им же самим диалога Платона «Тимей», в котором, действительно, нет рассуждений на какие-либо узко геометрические темы.
Но историческая тема ЗС ставилась шире: Белянин критиковал Стахова и за Пифагора и за Евклида тоже. В статье Белянина [1] говорится, что «выполняя деление отрезка в среднем и крайнем отношении, Евклид совершенно не апеллирует к пропорциональности, то есть фактически выполняет деление отрезка без понятия пропорции [т.е. без понятия о ЗС]. По сути, в этом предложении Евклид ищет такое деление отрезка, когда площадь квадрата, построенного на большей части отрезка, равна площади прямоугольника со сторонами в виде всего отрезка и его меньшей части. В свете вышеизложенного приходим с неизбежностью к выводу, что от чисто геометрического деления отрезка в среднем и крайнем отношении в очень далеком прошлом до понимания золотой пропорции в ее современном толковании, дистанция огромного размера» [1].
Этот вывод Стахов опроверг. Но вот, что привлекло меня еще в приведенном отрывке. Здесь без всякой задней мысли Белянин пользуется терминами «большей» и «меньшей» части отрезка, за использование которых он будет критиковать Стахова. Всё это выглядит не совсем последовательно. Читатель видит, как критик до какого-то момента придерживался традиционной точки зрения, но вдруг начинает за нее стыдить своего оппонента.
22 Ноября 2009 года к статье Белянина [1] появился комментарий С.Л. Василенко: «Жалею только об одном, что не прочитал эту красивую, добротную и честную работу раньше». Статья Василенко [2], написанная в поддержку позиции Белянина, вышла несколько раньше, этого комментария, а именно, 12 ноября.2009 года. Под заголовком «Критический анализ предшествующих работ» Василенко критически оценивает позицию Стахова, ссылаясь, в том числе, и на статьи Белянина. При цитировании [2] я изменю нумерацию ссылок, которая будет соответствовать библиографическому перечню данной статьи.
«Есть авторы, — пишет Василенко, — которые десятилетиями заявляют о том, что ЗС якобы родилось буквально из уст Пифагора, Платона и Евклида, и ни разу не удосужились проанализировать надежные первоисточники, в основном ограничиваясь вольным пересказом других не менее вольных пересказов 2–3-го и большего порядка. Но делается это так уверенно, будто озвучивается истина в последней инстанции. Например, в работе [3] читаем: "Из «Начал Евклида» известен следующий способ геометрического построения ЗС с использованием линейки и циркуля. Построим прямоугольный треугольник ABC со сторонами AB = 1 и AC =1/2...".
Далее можно не цитировать, поскольку становится очевидным, что автор даже не заглядывал в книги. У Евклида подобных построений с прямоугольным треугольником и близко нет. … Или в статьях [4, 5] находим [приводится еще примеры] …
Те, кто привык работать с научной литературой, не могли не заметить "выдаваемого эрзаца вместо текста Евклида" [6] и высказали мнение об "использовании каких-то прошедших через десятые руки формулировок не первой свежести" [7].
Особо обращалось внимание на то, что Евклид не выражал предложение 2.11 в приведенном виде, ни разу не вставлял в утверждения латинские буквы. У него нет слов "на две неравные части", нет слов "больший" и "меньший". Древнегреческие математики не писали "площадь квадрата" или "площадь прямоугольника" и т.п.
На эти замечания последовал ответ со смещением акцентов, в частности: "Белянин не согласен с установившимся (?) мнением, что именно Пифагор, Платон, Евклид были первыми из тех, кто обратил внимание на особую (?) роль ЗС в структурах Мироздания (?)" [4]. В другой интерпретации эта мысль представляется уже "традиционной точкой зрения на историю ЗС".
Подобные суждения нельзя оставить без внимания:
1) Виктор Белянин, конечно, говорил о других вещах, а здесь налицо искажение смыслов и безапелляционность суждений, густо усыпанных утверждениями сомнительного толка.Из статьи [8] мы, наконец, узнаем, откуда появились вышеупомянутые эрзацы-определения, "достаточно обратиться к книге канадского математика Roger Herz-Fishler [9], которая является наиболее известным в мире источником информации по математической истории ЗС. В этой книге на с. 8 Теорема II.11 приведена в следующей редакции: Theorem II.11 (the area formulation of DEMR). To divide a line AB into two segments, a larger one AH and a smaller one HB, so that S(AH) = R(AB, BH)"…
2) Установившихся мнений в освещении исторических событий далекого прошлого просто быть не может. Могут быть разные мнения с той или иной степенью достоверности, определяемой человеческим сообществом на основании собственных субъективных оценок.
3) Упомянутые ученые древности в своих математических рассуждениях касались темы ЗС не утилитарно, а отвлеченно (включая построение тел) и без всякого выделения особой роли даже в абстрактной математике, не говоря уже о реальных структурах Мироздания (what is it?).Получается, что нам ранее преподносили как формулировку Евклида, на самом деле является перевод вольного изложения некого интерпретатора. Вообще-то об этом следовало бы сказать еще раньше в работах [4, 5] и естественно сделать ссылку (!) …
Теорем у Евклида нет! Однако среди общего названия предложения некоторые из них можно воспринимать как теоремы, а иные как таковыми, что сейчас называем задачами на построение. Хотя, безусловно, для Евклида это гораздо больше, чем задачи на построение; это доказательство существования [10 (1948), c. 256], которое играет ключевую роль в самой геометрии. Конкретно предложение 2.11 как раз относится к утверждениям такого рода, но на теорему оно и отдаленно не похоже.
В целом, когда мы говорим о геометрии вообще, то возможны различного рода расширенные записи с буквенной символикой, различными уточнениями. Но если мы обсуждаем историю вопроса ЗС на языке Евклида, то подобное просто недопустимо.
Автор также волен интерпретировать любое научное суждение на свой лад. Лишь бы не доводить его до абсурда или вносить в него заведомо неприемлемые вещи.
Возвращаясь к Евклиду, мы видим: никаких больших и меньших отрезков у него в формулировке нет! Никаких неравных отрезков — тоже нет. Они появляются потом, в ходе решения задачи. Буквы в формулировках отсутствуют. Но они могут использоваться в доказательствах. Одним словом не история ЗС, а красивый суррогат.
Но года идут. И вот известное предложение Евклида обрастает, как всегда без ссылок, новыми всходами-отростками щупалец, но уже даже не как теорема, а исторически первое чудо-определение ЗС (?) [11]:
Теорема II.11 (Евклидово определение ЗС). Данную прямую AB = a разделить точкой C на две неравные части АС = b и CB = c (АС > CB) так, чтобы прямоугольник, заключенный между прямой АВ и меньшим отрезком CB, был равен квадрату, построенному на большем отрезке AC.Все музы просто внимают и молчат... Комментарии излишни... Не хватает только интеграла в бесконечномерном пространстве Фибоначчи...Читая подобные материалы, невольно приходишь в недоумение: столько работать в области ЗС, столько раз отмечать приоритет Евклида в ЗС и только сейчас приходить в восторг о частичном подтверждении этих мыслей в "Началах" самого Евклида (в переводе Мордухай–Больлвского), изданных на русском 60 лет назад. Именно эта линия и была главным предметом правильного и неоднократного возмущения авторского коллектива в лице Виктора Белянина и Андрея Радзюкевича.
Евклидову геометрию можно и даже должно изучать по разным современным учебникам математики без переводов оригинала. Но если уже писать об истории ЗС и о том, как она изложена у того же Евклида, просто не понятно, как можно пользоваться литературой второго-третьего пересказа, и не заглянуть в тексты самого Евклида.
Вот так часто и рождается легковесность и эрзацы в историчности ЗС под разными майонезами-соусами и приправой. Мало кто сомневается, что история ЗС насчитывает не одно тысячелетие. Весь вопрос, какие смыслы и понятия в него вкладывали ученые древних веков?» [2].
*
* *Напомним, процитированный только что текст Василенко был опубликован 12.11.2009, а на следующий день, 13.11.2009, была опубликована статья Стахова Деление отрезка в крайнем и среднем отношении и Золотое Сечение — это одна и та же задача? Знали ли Пифагор, Платон и Евклид о золотом сечении? Таким образом, Стахов писал нижеследующую статью [12], не зная о статье Василенко [2]. Поэтому, не комментируя фрагмент статьи [2], приведем стык в стык целиком статью [12], в заголовке которой строят вопросы. Ориентируясь на них, Стахов пишет:
«Ответы на эти вопросы содержится в комментарии Мордухай-Болтовского [М-Б], авторитет которого не вызывает сомнений (у меня, по крайней мере) [начало комм. М-Б]:
"Теперь посмотрим, какое место занимает золотое сечение в Началах Евклида. Прежде всего, нужно отметить, что оно встречается в двух формах, разница между которыми почти неощутима для нас, но была очень существенной в глазах греческого математика V-VI-го веков до н.э. Первая форма, прототип которого мы видели в Египте, является в Книге II Начал, а именно в Предложении 11 вместе с вводящими его предложениями 5 и 6; здесь золотое сечение определяется как такое, в котором квадрат, построенный на большем отрезке, равняется прямоугольнику на всей прямой и меньшем отрезке. Вторую форму мы имеем в определении 3 книги VI, где золотое сечение определяется пропорцией — как вся прямая к большему отрезку, так и больший отрезок к меньшему — и называется делением в крайнем и среднем отношении (ДКСО); в этой форме золотое сечение могло быть известным только со времен Евдокса. Интересно отметить, что предложениям 5, 6 и 11 книги II соответствуют предложения 27, 28 и 30 — шестой. Затем, предложения 5 и 6 книги II разорвали связь между предложениями 4 и 7, соответствующим нашим формулам квадратов суммы и разности; "та же фигура", о которой упоминается в предложении 7, строится в 4-м.
В книге XIII золотое сечение является в обеих указанных формах, а именно в первой форме в предложениях 1-5 и во второй — в предложениях 8-10. Правда в формулировке и тексте доказательства 1-5 предложений встречаются слова "в крайнем и среднем отношении", в доказательствах есть некоторые следы пользования пропорциями, но при внимательном чтении нетрудно заметить, что все эти места не связаны органически с общим текстом и легко из него могут быть исключены; все доказательство по существу ведется исходя из равенства на большем отрезке прямоугольнику ... Более того, предложение 2 книги XIII по существу равнозначно геометрическому построению предложения 11 книги II.
Все это позволяет думать, что предложения 4, 7, 8 книги II и предложения 1-5 книги XIII представляют остатки одного из самых древних в истории греческой геометрии документов, восходящего по всей вероятности к первой половине V века и возникшего в пифагорейской школе на основании того материала, который был привезен из Египта. Сравнительную древность этого документа можно установить из того обстоятельства, что предложения 4 и 7 книги II служат в ней для доказательства обобщенной теоремы Пифагора [квадрат стороны против острого и тупого угла (предложения 12 и 13 книги II)], которая, несомненно, была известна Гиппократу Хиосскому ... Несмотря на то, что первые пять предложений книги XIII составляют одно целое с рядом предложений книги II , нужно отметить, что при непосредственном использовании предложений книги II (в особенности предложения 11, которое и дает построение золотого сечения) доказательства были бы в отдельных случаях значительно проще" [конец комм. М-Б].
Мы можем сделать, — пишет Стахов, — следующие выводы из этих комментариев:
1. Однозначный ответ на первый вопрос: ДКСО и ЗС — это одна и та же задача! Так что Виктор Белянин не прав, утверждая обратное!
2. Второе, в Началах Евклида имеется не одна (Предложение II.11), а, по крайней мере, две различные формулировки задачи о золотом сечении. Цитирую М-Б: «Вторую форму мы имеем в определении 3 книги VI, где ЗС определяется пропорцией — как вся прямая к большему отрезку, так и больший отрезок к меньшему — и называется ДКСО; в этой форме золотое сечение могло быть известным только со времен только со времен Евдокса». И далее: «В книге XIII золотое сечение является в обеих указанных формах, а именно в первой форме в предложениях 1-5 и во второй — в предложениях 8-10». То есть, Евклид широко использует в своих Началах как первую форму (Предложение II.11 и предложения 1-5 книги XIII), так и вторую форму как представление золотого сечения в виде пропорции (предложение 3 книги VI и предложения 8-10 книги XIII).
3. Цитата М-Б ставит жирную точку в споре о том — знали ли Пифагор и Платон о золотом сечении? В задаче о золотом сечении М-Б видит "египетский след" и явно намекает на Пифагора, который 22 года провел в Египте и привез оттуда огромное количество египетских математических знаний, включая «теорему Пифагора» и золотое сечение. Отсюда вытекает, что М-Б не сомневался в том, что не только Евклид, но и Пифагор (а отсюда следует, что и Платон, который был пифагорейцем), а также и древние египтяне знали о золотом сечении и широко его использовали (вспомним о "Пирамиде Хеопса", "панелях Хеси-Ра" и др.).
Теперь о формулировке Предложения II.11 (или Теоремы II.11). В своих работах я использую формулировку, приведенную в книге канадского математика Roger Herz-Fishler “A Mathematical History of the Golden Number” (1998). Эта книга является наиболее известным в мире источником информации по математической истории золотой пропорции. В этой книге на с. 8 Теорема II.11 приведена в следующей редакции:
Theorem II.11 (the area formulation of DEMR). To divide a line AB into two segments, a larger one AH and a smaller one HB, so that S(AH) = R(AB, BH).
Если теперь учесть, что S(AH) – это площадь квадрата, построенного на стороне AH, то есть большей стороне, а R(AB, BH) – это площадь прямоугольника со сторонами AB и BH, то указанную выше Теорему II.11 можно перевести на русский язык следующим образом:
Теорема II. 11. Данную прямую разделить на две неравные части АС и СВ так, чтобы площадь квадрата, построенного на большем отрезке АС, равнялась бы площади прямоугольника, построенного на отрезке АВ и меньшем отрезке СВ.
Именно так я перевел текст Теоремы II.11 из упомянутой книги.
Я, конечно, не знаю, из какого из 31 "первоисточников" Евклида Roger Herz-Fishler взял именно такую формулировку Теоремы II.11, но вполне уместно предположить, что в одном из них эта теорема сформулирована именно в таком виде, который не совпадает с русским переводом Начал Евклида.
Хочу обратить внимание на то, что Roger Herz-Fishler использует слово Теорема вместо слова Предложение (суть задачи от этого не меняется). Возникает вопрос, какая разница между теоремой и предложением? В Википедии читаем: "В математических текстах теоремами обычно называют только достаточно важные утверждения. При этом требуемые доказательства обычно кем-либо найдены ... Менее важные утверждения-теоремы обычно называют леммами, предложениями, следствиями, условиями и прочими подобными терминами. Утверждения, о которых неизвестно, являются ли они теоремами, обычно называют гипотезами". Так что разницы между теоремой и предложением по существу нет. Roger Herz-Fishler использовал название Теорема II.11, поскольку он считал это предложение достаточно важным утверждением (с точки зрения золотой пропорции).
Кстати, Roger Herz-Fishler утверждает, что в Началах Евклида имеется 84 теоремы (или предложения), имеющие отношение к золотой пропорции! На этом основании мы можем сделать вывод, что золотое сечение буквально пронизывает Начала Евклида от 1-й до 13-й книги!
Если мы соглашаемся с этим фактом и учтем замечание наиболее авторитетного в мире историка математики Ван-дер-Вардена о том, что Начала Евклида на 2/3 состоят из результатов пифагорейцев, то это дает нам все основания признать, что Пифагор, пифагорейцы и Платон (который считал себя пифагорейцем) знали золотое сечение и широко его использовали! Об этом, по существу, говорит и М-Б в своих комментариях, намекая на египетский след при обсуждении предложений или теорем, связанных с золотой пропорцией. И знание о золотом сечении Пифагор привез из Египта вместе с другими геометрическими знаниями.
А если учесть гипотезу Прокла об истинных целях, которые преследовал Евклид при написании своих Начал (создание завершенной теории Платоновых тел), то становится ясным, зачем Евклид ввел золотое сечение уже в Книге II, а затем многократно возвращается к нему в последующих книгах, включая Книгу XII. А ввел он эту задачу с единственной целью — построить геометрическую теорию додекаэдра, гранями которого являются пентагоны! И из гипотезы Прокла вытекает еще один необычный вывод: Начала Евклида являются исторически первой Математической Теорией Гармонии Мироздания, которая ассоциировалась у древних греков с Платоновыми телами.
Комментируя пространные рассуждения моего оппонента по поводу Начал Евклида, хочу отметить, что мне эти рассуждения показались неубедительными. Сначала кажется, что измышлизмы оппонента имеют какой-то смысл, тем более что оппонент пытается демонстрировать глубочайшие знания Начал Евклида, но, когда статью дочитываешь до конца, перестаешь понимать, что же хочет сказать мой оппонент в своем очередном опусе. То есть это опять очередная порция квазинауки, которая не привносит ничего нового в теорию чисел Фибоначчи и золотого сечения.
В названии этой заметки поставлены два вопроса. Абсолютно неясно, как оппонент отвечает на эти вопросы в своем опусе. Если оппонент придерживается мнения Виктора Белянина о том, что ДКСО и ЗС — разные задачи, то он выступает против мнения всего мирового научного сообщества на эту проблему, в частности, против мнения М-Б. Если оппонент придерживается «учения Белянина-Радзюкевича» о том, что Пифагор, Платон и все пифагорейцы не ведали о золотом сечении, то абсолютно непонятно, как золотое сечение попало в Начала Евклида и как объяснить фразу М-Б о том, что "золотое сечение могло быть известным только со времен Евдокса".
Как известно, великий геометр Евдокс Книдский жил в период с 408 до н. э. до 355 до н. э., то есть, он был современником Платона (427 до н. э. – 347 до н. э.). Как сообщается в Википедии, он учился математике у пифагорейца Архита в Италии, затем присоединился к школе Платона в Афинах. М-Б приписывает Евдоксу знание золотое сечение. Но неужели Евдокс не рассказал Платону о золотом сечении, когда он присоединился к Платоновой Академии?
Я обращаюсь к моему оппоненту с просьбой не тиражировать глупости, высказанные в свое время Беляниным и Радзюкевичем с единственной целью — попиариться на золотом сечении» [12].
*
* *В комментарии М-Б говорится о двух формулировках золотого сечения. О них пишет и Василенко: «Золотое сечение в его современном представлении встречается в Началах Евклида в двух формах, которые весьма различны и довольно далеки друг от друга в глазах греческого математика IV века до н. э. Первая форма связана с отношением и равенством площадей [10 (1948), с. 75]:
Предложение 2.11. Данную прямую рассечь так, чтобы прямоугольник, заключенный между целой и одним из отрезков, был равен квадрату на оставшемся отрезке. То есть линия делится так, что больший отрезок является средней пропорциональной между всей линией и меньшим отрезком. О всяком прямоугольном параллелограмме говорят, что он заключен между двумя прямыми, образующими прямой угол (определение 2.1). Не исключено, что похожие формы были известны еще ранее египтянам.
Вторая форма известна как задача деления отрезка в крайнем и среднем отношении (КСО), и впервые ее описание звучит следующим образом:
Определение 3.6. Говорится, что прямая делится в крайнем и среднем отношении, если как целая к большему отрезку, так и больший отрезок меньшему [10 (1948), с. 173].
Построение, похожее на 2.11, приведено в предложении 6.30: данную ограниченную прямую рассечь в крайнем и среднем отношении [10 (1948), с. 213]. Хотя там уже другие буквенные обозначения, нежели в первой форме. А доказательство идет через пропорциональность отрезков и нахождение большего из них» [2].
Читатель знает, что я не питаю больших симпатий к Стахову: он любит подхалимов, а мне они противны. Чего стоит льстивое послание гуманитария Льва Семашко, в котором звучит обещание выдвинуть математика Стахова на Нобелевскую премию (см. послание Революция в математике), а сам Стахов предлагает дать гуманитарию Эдуарду Сороко Нобелевскую премию за его математическую разработку (см. Вклад белорусского философа…). Наблюдать за этой «раздачей» самой почетной награды мира без улыбки не возможно. Но какие бы субъективные чувства нас не одолевали, объективно мы всё же должны встать на сторону Стахова.
Кстати, специально для Стахова и Семашко добавлю. Не будьте так наивными: Нобелевская премия дается главным образом по политическим соображениям, наука здесь стоит на втором сильно удаленном плане. Нужны примеры? Пожалуйста, практически все советские лауреаты: Ландау, Гинзбург, Тамм и Франк. Относительно трех последних становится кое-что понятно, если прочитать здесь и здесь. Кто достоин ее? Кастерин, например, но ему не давал работать Иоффе (о нём здесь). Для начала можно почитать Протокол и резолюцию по делу Н.П. Кастерина.
Но это так, между прочим, а теперь о буквах. Действительно, в первой форме золотой пропорции их нет. В формулировке предложения (теоремы) 2.11, приведенной Стаховым по [9], введены буквенные обозначения, которые, однако, никакого принципиального значения не имеют. Их нет не потому, что Евклид жил в далекую эпоху, когда буквенная символика математиками не использовалась. Отсутствие их не свидетельствует также о каком-то особом мышлении математиков той далекой поры. Их нет потому, что предложение 2.11 «глаже» звучит с точки зрения восприятия на слух. Ученик обязан был запомнить десятки подобных предложений. Чтобы «не спотыкаться» о буквы, привязанные к чертежу, и облегчить запоминание существа дела, учитель убрал их. Нельзя не видеть, что текст аксиом, постулатов и теорем (предложений, требующих обоснование) евклидова учебника рассчитан на заучивание.
Теперь о самом большом «преступлении» г-на Стахова. Плохо, конечно, что он не указывал на источник, откуда берется та или иная цитата. Однако такое отношение к литературным источникам можно понять. Возможно, оно выработалось в связи с частой повторяемостью понравившихся ему цитат. Например, отрывок из Лосева, начинающийся со слов «С точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления — Золотого Сечения», Стахов повторял многократно в различных своих статьях, но источник (журнал «Коммунист», 1981, №11) указал только однажды, в статье «Вклад белорусского философа Эдуарда Сороко в развитие общей теории Гармонии и Золотого Сечения» Кстати, первым эту цитату из Лосева привел именно Э.М. Сороко.
Так ли уж принципиален спор о словах «предложение» и «теорема»? Нет, особенно, если учесть, что термин «теорема» всплыл по вине Герц-Фишлера (Herz-Fishler), а не Стахова. Василенко написал: «Просто удивительно, почему многие в отправной информации так тянутся к словам о "квадрате на большем отрезке " или "прямоугольнике — на малом ". Так уж принципиально нужны слова "большое — малое" в контексте начального условия? Конечно, нет» [2]. А если «нет», то зачем об этом столько говорить?
Пусть не в начальном предложении, но слова «большое — малое» вместе с буквенными обозначениями Евклид всё-таки использует. Василенко дает подробную «геометрическую интерпретацию предложения 2.11» (рис. 1 – рис. 5, взятые из [2]), доказывая неуместность уточняющих слов "большое — малое".
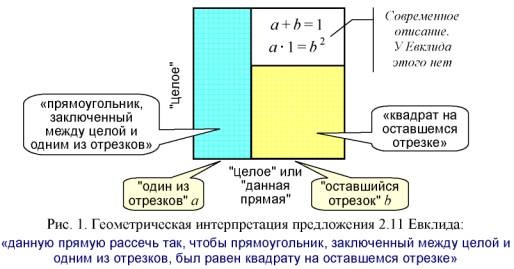
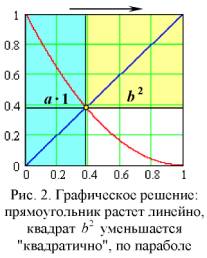
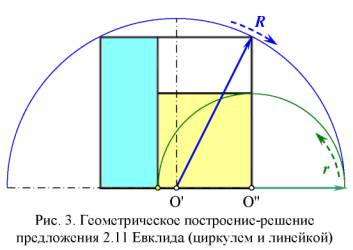
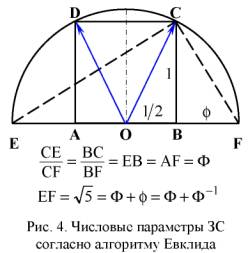
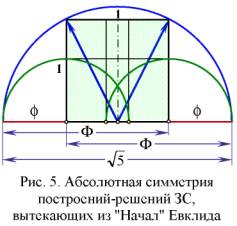
Пускай наш критик прав на 100 процентов. Но какое отношение всё это имеет к существу спора: знал или не знал Евклид о золотой пропорции? Ответ — самое прямое. Василенко, критикуя Стахова за неточность формулировок предложения 2.11, нечаянно доказал, что александрийский математик прекрасно знал о золотой пропорции — а ведь именно это являлось камнем преткновения в споре. Да, слегка изменена софистическая стилистика предложения 2.11. И сделал это, между прочим, канадский авторитет, на которого положился Стахов. Можно в этом месте поднять брови и с напускным возмущением воскликнуть: «Как? Да вы не понимаете разницы между мышлением древних и современных математиков!»
Но что значит фраза: «ученые древности в своих математических рассуждениях касались темы золотой пропорции не утилитарно, а отвлеченно»? Бывало по-разному: одни ученые, например Евклид, использовали золотую пропорцию для построения правильных многогранников и мало думали о всеобщей гармонии, другие, например Платон, — для строительства эстетически привлекательного мироздания в целом. Все три «суждения» Василенко, которые «нельзя оставить без внимания» при не предвзятом взгляде кажутся мне не столь принципиальным в деле выяснения значимости золотой пропорции для картины мира образованного человека Древней Греции.
Василенко на многое закрыли бы глаза, если бы его не раздражала сама личность Стахова. В справедливости постановки исходной проблемы он сильно сомневается: «Сказать, что Евклид, а заодно и древние геометры, не знали о специфичном делении прямолинейного отрезка на две неравные части, язык не поворачивается. Поскольку есть положения (предложения), которые, так или иначе, решают данную проблему. Но и сказать, что Евклид знал о золотой пропорции, значит сильно слукавить и ввести в заблуждение читателя. …
Скорее всего, наш начальный вопрос нельзя назвать корректным. Да, Евклид ходил вокруг этой проблемы. Касался ее. Порой перешагивал. Решал. Тут же перескакивал на другие задачи. Потом возвращался, но уже в ином качестве и даже с другими буквенными обозначениями, наиболее вероятно, пересказывая других авторов без увязки в общей структуре или контексте повествования. А это верный признак отсутствия особых предпочтений. На фоне остальных, — так просто рядовая задача.
Да, он формировал геометрические построения. Но совершенно никак не выделял эту задачу среди остальных и не придавал ей какого-либо отличительного значения. А в пропорциях-отношениях она вообще отсутствует, как таковая. Более того, у Евклида нет понятия отношения чисел, хотя присутствует «отношение... однородных величин по количеству» (определение 5.3 [10 (1948), c. 142]).
А вот понятие пропорциональности есть уже как для величин, так и для чисел, но они проводятся независимо (раздельно), поскольку он еще не «в силах охватить эти два понятия ... в одном общем их объемлющем понятии пропорциональности вообще, ... так что общим у них остается только название» [10 (1948), c. 372].
Может быть, он и выстраивал какую-либо концепцию, похожую на золотую пропорцию в ее современном представлении, но в материалы она не вошла. Это, примерно, все равно, что спрашивать, знали ли древние числа? Безусловно, знали. Но разве в том объеме и с теми многочисленными новыми свойствами как сегодня? Конечно же, и близко нет. Например, «Евклид нигде не оперирует отношениями как с числами» [10 (1948), c. 408]. «Для Евклида число — это собрание единиц (определение 7.2), так что дробь для него еще не является числом. Между геометрическими величинами и числами еще нет взаимно однозначного соответствия» [10 (1948), с. 371]. «У Евклида нет дробей... Абстрактная дробь заменяется отношением целых чисел, применение которого основывается на высокоразвитой теории пропорций» [10 (1949), с. 265].
Что подумалось еще. Допустим, что древние ученые знали о золотой пропорции, скажем, почти в современном представлении. Спрашивается, а что же тогда человечество приобрело в этой части со времен Пифагора, Евклида или Платона? Получается, ничего. Ну, разве что осовременили алгебраической геометрией в виде решения квадратного уравнения. И все!? Даже числа Фибоначчи здесь ни при делах, поскольку согласно теореме Бернулли они выражают общие свойства всех последовательностей стремиться к максимальному корню алгебраического уравнения, которое их порождает. Кроме того, у них совершенна иная онтология, нежели у золотого сечения, хотя они и связаны где-то далеко в бесконечности.
Что-то здесь (в такой постановке вопроса) явно не сходится.
Посмотрим на вопрос ЗС с другой стороны. А что вообще меняет усиление или ослабление позиции о степени знаний ЗС древними? Допустим, мы скажем, что знали, но не очень. Или скажем, да знали и очень хорошо. С позиции нынешних представлений в этом вопросе ничего не меняется. Это уже в прошлом. Хотя нет, — скорее всего, «история золотого сечения лишится ореола древности, что приведет к существенному изменению» [7] навязываемой идеологии либо смене акцентов в чьих-то личных амбициях.
На наш взгляд, важнее не то в каком объеме знали это древние (что подобные знания были, сомнений нет), а что мы знаем сегодня и какие у нас есть перспективы на завтра. И есть ли они вообще? Ведь может так статься, что все это утопия или красивая сказка для убеленных сединой ученых.
А теперь еще раз вернемся к крайней точке зрения: древние знали ЗС очень хорошо и в полном объеме. Спрашивается в задаче, тогда почему же до сих пор за столько времени эти знания практически ничем не усилились ни в физике, ни в математике, разве что числами Фибоначчи. Но это уже "из другой оперы", у которой совершенно иная систематика, причем верная практически для любого алгебраического уравнения и соответствующих числовых последовательностей. Тогда получается, что ЗС — метафизическая фантазия, которая закончилась в прошлые века вместе с алхимией. — Неутешительный вывод, но он логически и почти автоматически следует из концепции основательного знания теории ЗС в античные времена.
Так или иначе, но в целом можно уверенно говорить, что история ЗС восходит к Евклиду, а еще ранее и к пифагорейцам. Но утверждать что «ЗС пронизывает все книги Евклида» (А. Стахов), — по меньшей мере, наивно. Тем более, слышать подобное от людей, которые за свою жизнь ни разу самих книг Евклида (пусть даже в переводе) и не открывали» [2].
*
* *Как бы сказать про это словоблудие помягче? Скажем так: критик в растерянности, он вконец запутался, но всё же не теряет надежды выкрутиться, объявив главный вопрос не корректно поставленным.
Почему о некорректности Василенко заговорил в конце статьи, а не в ее начале? Потому что он почувствовал свой проигрыш.
Какой вывод из статьи [2] должен сделать читатель? Стахов выиграл спор и с Беляниным и с пришедшим к нему на помощь Василенко, причем без всяких "но".
Не нужно придираться к словам: золотое сечение «пронизывает все книги» Евклида. Достаточно того, что золотое сечение слишком часто упоминается в «Началах», а это как раз и говорит в пользу того, что александрийский математик выделял его из всех остальных сечений. Сам Василенко привел пять первых предложений из 13-й книги «Начал», свидетельствующие о глубоком понимании Евклидом и, следовательно, пифагорейцами замечательных свойств золотой пропорции:

Возможно, это произошло невольно, поскольку александрийский математик опирался на пифагорейские книги, где золотое сечение досконально изучалось. Но оно есть в «Началах» и его там много — данный факт «наивно» отрицать. Поскольку золотое сечение упоминается много раз, само собой разумеется, что Евклид и авторы книг, которые использовались им для написания «Начал», выделяли его из всех остальных сечений (пропорций).
То, что Стахов в своих статьях не указывал страницы «Начал», это, конечно, плохо. Но это еще не означает, что он за свою жизнь ни разу не открывал сочинения Евклида, как об этом обидно сказал Василенко. Он ведь не рассчитывал, что традиционная точка зрения подвергнется ожесточенной атаке со стороны Белянина и Василенко.
Начал Василенко бодро: у Стахова «одним словом, не история золотое сечение, а красивый суррогат», презрительно сказал он. Но потом — и мы были тому свидетелями — уверенность лихого критика куда-то испарилась, он почувствовал невесомость своих аргументов и стал смешно кувыркаться в пространстве пустых слов. По-видимому, М-Б, т.е. комментатор и переводчик на русский язык «Начал» [10], убедил его, что Евклид таки прекрасно знал золотое сечение, но так как «книга II берет свои начала еще от пифагорейцев» (слова, повторенные за М-Б самим Василенко), то золотое сечение знал и Пифагор.
Чтобы еще раз посмотреть, как беспомощно барахтается Василенко, поставим рядом несколько наиболее ярких предложений конца его статьи: «Сказать, что Евклид, а заодно и древние геометры, не знали о специфичном делении прямолинейного отрезка на две неравные части [т.е. о ЗС], язык не поворачивается. Поскольку есть положения (предложения), которые, так или иначе, решают данную проблему [о ЗС]. Но и сказать, что Евклид знал о золотой пропорции, значит сильно слукавить и ввести в заблуждение читателя. …Но в целом можно уверенно говорить, что история ЗС восходит к Евклиду, а еще ранее и к пифагорейцам» [2].
На этом закончим разбор спора между Стаховым и Василенко по вопросу, поднятому Беляниным. Далее пойдет разговор о золотой пропорции, никак не связанный с историей математики.
От теории РЗС к раковине Nautilus pompilius
Чтобы раскрыть читателям гармоническое мировоззрение Сергея Василенко и его медленную трансформацию, я позволю себе процитировать постановку задачи статьи [21], написанную им, когда вера в тотальное присутствие ЗС в нашем несовершенном мире у него слегка зашаталась. К этому времени он успел навлечь на себя гнев Стахова, усомнившись в правомерности понятия «обобщенного ЗС». О конфликте с директором Института ЗС я расскажу позже, а сейчас обещанная цитата.
«В теоретических и практических исследованиях, — пишет Василенко, — часто встречаются задачи на конечно-дискретных математических объектах. Их изучение предполагает поиск решений в виде целочисленных переменных. В теории чисел известно целое направление по исследованию структур, описываемых диофантовыми уравнениями с целыми коэффициентами и неизвестными, которые могут принимать только целые значения.
Например, мы хотим поделить группу из 50 человек в "золотой" пропорции. Вследствие иррациональности числа Φ осуществить такое деление точно невозможно. Но это вовсе не означает, что мы не в состоянии проделать это так, чтобы наилучшим образом наше деление приблизить к ЗС, и не оправдываться за то, что операция выполнена не ровно по ЗС, а только приблизительно, как в известной арифметической задачке про "полтора землекопа". Поэтому деление нашей группы в отношении 31:19 следует рассматривать не ориентировочным, а точным ЗС, — в смысле наилучшего приближения к Φ в целочисленных переменных.
Как особый частный случай традиционной "золотой" пропорции, приводящей обычно к иррациональным результатам, ЗС в целых числах назовем рациональным» [21].
Несмотря на этот «особый частный случай» золотого сечения он, тем не менее, приобретает общефилософское значение. «Иррациональное ЗС, — пишет Василенко, — несмотря на его изящность и эстетичность, в чистом виде себя практически не проявляет хотя бы потому, что своей идеальностью не оставляет ни одного шанса на наличие внутрисистемных связей, чем целое отличается от просто суммы своих слагаемых.
Если бы природа действовала исключительно на основе безупречного значения Φ со всеми его миллиардными знаками после запятой, она просто не смогла бы развиваться, зациклившись на своем идеале, у которого, нужно сказать, "мертвая хватка" в прямом и переносном смысле. В этом смысле число Φ — это летальный исход или приговор обновлению, совершенствованию и вообще любому развитию.
Безусловно, что в мироустройстве очень многое, если сказать не почти все, "крутится" вокруг золотого сечения. И анализ наблюдаемых процессов, явлений, живых объектов это показывает. Но их синтез шел и продолжается далее в своем развитии по другим законам, где число Φ, если и играет доминирующую роль, то не в своем идеальном проявлении, — типа деления в крайнем и среднем отношении. Его уникальная математическая конструкция не способствует образованию "дельты", отвечающей за системность целого. Попадая точно на Φ, объект теряет системные связи и свою целостность, а значит разрушается. Живое, попадая в его заколдованный круг, перестает быть таковым.
Возможно, для всех биотических тел число Φ является главной причиной их тленности, и в этом его одно из главных проявлений и предназначений. Поэтому процессы синтеза и сегодня продолжающаяся эволюция миропорядка, скорее всего, идут в целочисленном измерении…» [21].
Логика этих философских рассуждений меня поражает. Так и хочется воскликнуть: «На каком основании!» Автор окинул единым взором необъятную Вселенную и увидел, что всё бесконечное число физических величин стремится к абстрактному пределу — Φ, немного не дотягивая до него. «Снимите розовые очки, товарищ, через них вы ничего не видите!» Иррациональное число Φ или близкие к нему рациональные дроби в природе встречаются не чаще, чем корень квадратный из двух и близкие к нему значений. Класть в основание мироздания какие-либо числа — будь то Φ, π, e или 10 — значит, перенести себя на две с половиной тысячи лет назад, в эпоху Пифагора, когда не было ни одной мало-мальски верной физической теории.
Василенко прекрасно ориентируется в современной математике, но при этом придерживается какой-то дремучей нумерологии пифагорейцев. Его «Заметки по РЗС в анатомии человека», иллюстрирующие идею последнего процитированного мною абзаца, вполне подтверждают эту древнюю философию, которой придерживались также древнекитайские авторы Книги Перемен, алхимики и т.д. Он пишет: «Существует разнообразные описания "золотой" пропорции в фигуре (размерах и частях тела) человека (Леонардо да Винчи, Цейзинг А., Коробко В.И.), сердечных структурах (Цветков В.Д.), ритмах мозга (Соколов A.A.) и др. …
…Без особой детализации предлагается авторский схематичный набросок (рис. 1) в части возможного синтеза анатомического строения человека на базе общих подходов РЗС. В основу построения положено число 2 5 = 32. Скажу откровенно, довольно произвольно. Возможно, потому, что связка 2–5 является ключевой в числе

Кроме того, здоровые зубы — залог долголетия» [21]. В том, что это не шутка, убеждает нас аккуратно вычерченная схема (рис. 1) и подробные разъяснения к ней.
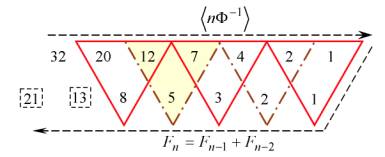
Рис. 1. Схема рациональных золотых сечений (РЗС) в анатомическом строении человека (по треугольникам и нижнему ряду — числам Фибоначчи):
- пальцы рук и ног как пограничная связь с внешним миром — 20
(то же самое с головой — 21, как число Фибоначчи)- весь организм: внешние (голова, руки, ноги — 5), основные внутренние органы (по варианту а) — 7: 12 = 5 + 7 — 12
(то же самое с туловищем — 13, как число Фибоначчи)- число пар ребер, число фаланг (3 x 4) — 12
- основные внутренние органы:
а) сердце, легкие (2), почки (2), печень, желудок, кишечник — 8
б) сердце, легкие, почки, печень, желудок, кишечник, половые — 7- парные органы: глаза, уши, ноги, руки, почки, легкие, половые — 7
в т.ч. внешние - 4, внутренние - 3: 7 = 3 + 4- органы чувств: зрение, слух, вкус, обоняние, осязание (кожа) — 5
в т.ч. одиночные — 3, парные — 2: 5 = 2 + 3
(при этом нос занимает промежуточное положение, и условно можно отнести как к парным, так и одиночным)- число пальцев на одной конечности — 5
- количество конечностей (из двух пар) 4 = 2 + 2 — 4
*
* *Чтобы проиллюстрировать абсурдность теории множества рациональных ЗС, которые не дотягивают до идеального иррационального ЗС, приведу несколько наглядных примеров.
В Интернете я нашел картинку «золотой» руки, которая с помощью Photoshop'a или другого графического редактора подогнана под ЗС. Очевидно, что идеальных «золотых» рук не бывает. Я измерил свою руку, как показано на рис. 2, получил два числа — 24 см и 18 см, которые дают, соответственно, 0.571 и 0.428 — ничего близкого к золотым числам 0.618 и 0.382. Но, согласно Василенко, природа стремилась к ЗС, но у нее со мной ничего не вышло.

Рис. 2. «Золотая» рука
Известно, что люди имеют различный вес, причем большинство из них попадает в диапазон от 50 до 150 килограммов. И вот находится группа фанатиков, которая уверяет всех, будто вес в 100 кг является идеальным, поскольку нет более круглого числа, чем сотня. С пропорциями частей человеческого тела происходит примерно то же самое. В общем, они меняются в широких пределах, но находятся гармонисты, которые объявляют идеально сложенными тех, у кого некоторые части тела находятся в отношении близком к числам Φ или φ.
А кто-нибудь обмерял баранов, верблюдов, обезьян, кошек, мышей, рыб, насекомых? Может быть, их пропорции ближе к золотым и встречаются чаще? Нет, никому это не нужно; легче и приятнее объявить человека венцом божьего творения. Пусть так, в конце концов, только предъявите, пожалуйста, нам доказательства этого «научного» факта в виде статистически обработанной выборки по русским, китайцам, жителям острова Пасхи. Ничего этого сделано не было. Так зачем же обманывать детей?
В природе существует сотни тысяч растительных видов, семена которых расположены как угодно, только не в соответствии с числами Фибоначчи. Из этой растительной массы нашли несколько видов (шишки, подсолнухи и маргаритки), где эти числа встречаются, и стали убеждать нас, что мир создан в соответствии с золотой пропорцией. Разумеется, семена имеют определенную форму, которая диктует структуру их упаковки. Семечкам подсолнуха, орешкам сосновой шишки и семенам маргаритки удобно располагаться в виде спиралей. Колосья пшеницы и ржи уже никаких чисел Фибоначчи не дают. Количество горошин и бобов в стручках тоже не удачное с точки зрения ЗС и т.д. Если бы лимоны умели говорить, они бы объявили число 10 священным, так как плоды цитрусовых деревьев делятся на десять сегментов, а яблоки только на пять.
Особенно мне «нравится» аргумент со спиралями. Нам говорят: посмотрите на рога горного козла (рис. 3), они завиты спиралью, которая связана с числами Фибоначчи и золотой пропорцией. Смотрим и видим, что рога изогнуты не в одной какой-то плоскости, а в трехмерном пространстве (на приведенных фотографиях это хорошо видно). Пойдем навстречу сторонникам универсального принципа и возьмем от этой сложной винтовой конструкции самую выгодную для них проекцию на плоскости. Даже в этом случае мы вовсе не уверены, что кривая от козлиного рога даст нужную спираль.

Рис. 3. Нам рассказывают, будто козлиные рога имеют отношение
к золотому сечению. Ну, не смешно ли это слышать?Несколько слов, что понимается под золотой спиралью. На рис. 4 изображен радующий глаз художника, но фальшивый с точки зрения математики кусочно-составной агрегат, отдаленно напоминающий логарифмическую спираль. Именно эту искусственную конструкцию эпохи зарождающейся науки часто именуют золотой или спиралью Фибоначчи, который, к слову сказать, никакого отношения к этому уродцу не имел.
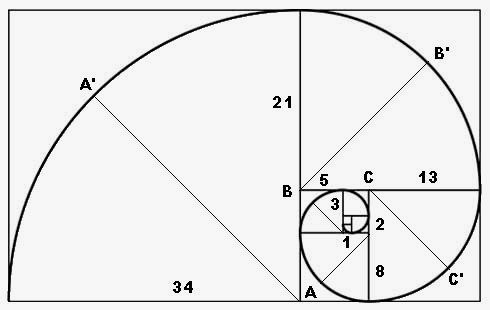
Рис. 4. «Золотая» спираль или спираль Фибоначчи
Из отрезков, находящихся в гармоническом отношении, можно построить систему квадратов и прямоугольников, и вписать в них спираль, как показано на рис. 4. Здесь следует иметь в виду: данная спираль складывается из четвертных секторов линий окружности с радиусами, равными числам Фибоначчи: AA' = 34, BB' =21, CC' = 13 и т.д. Такой кусочно-составной агрегат лишь приближенно копирует логарифмическую спираль, построенную в соответствии с формулой Бине.
Логарифмическая спираль обладает одним важным свойствам: луч, выходящий из полюса спирали, пересекает любой ее виток под одним и тем же углом. В спирали Фибоначчи это условие не выполняется, так как центр секторов окружностей постоянно меняется. Например, в нашем случае (рис. 4) для последней дуги центр находится в правом нижнем углу квадрата со стороной 34 (точка A), для предпоследней дуги центр находится в углу квадрата со стороной 21 (точка B) и т.д., хотя спираль началась в квадрате со стороной 1 — значит, там ее полюс.
Существует масса других спиралей. Наиболее популярными из них являются спираль натурального логарифма (рис. 5а), архимедова спираль (рис. 5b), гиперболическая спираль (рис. 5c) и спираль Ферма или жезл (рис. 5d); конкретные законы изменения этих спиралей приведены на соответствующих графиках.
Рис. 5a. Логарифмическая спираль.
Рис. 5b. Архимедова спираль.
Рис. 5c. Гиперболическая спираль.
Рис. 5d. Жезл (графики взяты с http://webmath.exponenta.ru)Чисто визуально, порой, трудно отличить архимедову спираль от логарифмической, гиперболическую от спирали Ферма. Нужно не забывать также, что костяные наросты животных имеют самую разнообразную форму; вспомните оленя, носорога, моржа, слона, мамонта. Если бы даже у какого-нибудь из этих животных они вырастали в соответствии со спиралью Фибоначчи, это еще не доказывало бы, что вся живая природа стремится к воссозданию золотой пропорции.
Тот же аргумент справедлив и в отношении ракушек, улиток и прочей живности, обитающей в водной стихии. Они — представители головоногих вроде медуз, осьминогов и кальмаров, которые, однако, не имеют своего уютного домика. У головоногих с внешним скелетом существует несметное количество форм, в том числе, и спиралевидной геометрии. Среди них, естественно, нашлись и такие, которые с некоторой погрешностью отвечают спирали Фибоначчи. Теперь на основании этого небольшого класса раковин стали говорить о каком-то мистическом проникновении закона золотой пропорции в бесконечный мир морских обитателей.
Я не поленился посмотреть специализированные книги на эту тему ([22] и [23]) и обомлел: такого разнообразия форм трудно найти на земле (рис. 6). Научное название этим обитателям моря — аммониты; данное слово появилось из древнеегипетской мифологии. Бог Амон имел рога овна (барана); жители Средиземноморья морские ракушки называли рогами Амона; отсюда произошел уже научный термин ammonitos. Термин аммоноид означает подобный аммониту. Некоторые нижеприведенные раковины имеют специфические названия, поскольку принадлежат более узким таксонам.
1  2
2  3
3 
4  5
5  6
6 
7  8
8  9
9 
10 11
11 12
12
13 14
14 15
15
16 17
17 18
18
19 20
20 21
21
22 23
23 24
24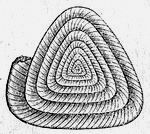
25 26
26 27
27
28 29
29 30
30
31 32
32 33
33
34 35
35 36
36
A
B
C
D
E
F
Рис. 6
Серия раковин 1 - 36
Данная серия, взятая из книги [22], призвана продемонстрировать многообразие форм раковин головоногих (внемасштабно).
Серия раковин A.
Силурийские брюхоногие: Eccyliopterus alatus из валуна нижнесилурийских пород; 2—3) Euomphaloplcrus alatus из верхнесилурийских отложений острова Готланда; 4) Salpingostomy megastoma из валуна нижнеенлу-рийского известняка; 5) Maclurea Logani с крышечкой, оттуда же; 8) Acroculia anguis из чешских силурийских отложений (по Ремеру). [22, с. 76, рис. 53].
Серия раковин B.
В зависимости от раковин различают три группы наутилоидей: прямые, изогнутые и спирально завернутые. Важнейшие типы внешнего облика наутилоидей. 1 — циртокон; 2 — гирокон; 3 — наутилокон (адволютный); 4 — наутнлокон (конволютный); 5 — литуикон; 6 — бревикон; 7 — трохикон (необъемлющий) (по А. Г. Мюллеру) [23, с. 162, рис. 2.29].
Серия раковин C.
Аммоноидей с пережимами на раковинах. Пережимы соответствуют замедленным фазам роста раковины и встречаются прежде всего на конечных стадиях эволюционных рядов (по А. Г. Мюллеру) [23, с. 166, рис. 2.36].
Серия раковин D.
Разнообразие форм устьев у различных аммоноидей (внемасштабно; по А. Г. Мюллеру) [23, с. 166, рис. 2.35].
Серия раковин E.
Важнейшие типы строения и внешнего облика раковины на конечных стадиях известных эволюционных рядов аммоноидей [23, с. 169, рис. 2.39].
Серия раковин F.
Некоторые типы оборотов раковины у аммоноидей (внемасштабно; по А. Г. Мюллеру) [23, с. 168, рис. 2.37].
Рис. 7. Наутилус помпилиус (Nautilus pompilius)
И вот, среди всего этого богатства форм нашелся один красавец — Наутилус помпилиус (Nautilus pompilius) — живое существо, которое за счет специальных внутренних перегородок, поддерживающих внешнюю форму, имеет раковину, изогнутую в соответствии с логарифмической спиралью (рис. 7).
Подчеркнем еще раз, логарифмическая спираль (рис. 5а) лишь отдаленно напоминает спираль Фибоначчи (рис. 4), а сами числа Фибоначчи имеют лишь косвенное отношение к золотой пропорции, на чем, между прочим, настаивает и сам Василенко. О чём здесь можно вести речь, когда предмет разговора у гармонистов-золотоискателей отчетливо не обозначен?
Всмотритесь как следует в сечения спиралей оксиконного, кадиконного и платиконного оборотов (рис. 6F), внешние очертания этих раковин не совпадают с их внутренним строением. Предположим, вам удалось найти раковину, внешне напоминающую спираль Фибоначчи. Будьте уверены, такое сходство является чисто случайным, не отражающим сложного строения внутренней части скелетов аммоноидей.
Вопреки заверению Василенко, жизнь не стремится к некоему золотому аттрактору, напротив, она бесконечно разнообразит свою геометрию, подстраиваясь под меняющиеся внешние условия. Вера в золотой аттрактор — это всего лишь вера. Откуда речной улитки знать о золтой пропорции.
Сколько было споров вокруг теорий Дарвина и Ламарка — всё оказалось напрасно: вера в предустановленную гармонию до сих пор жива. Разумеется, никто из серьезных специалистов по раковинам, включая авторов книг [22] и [23], не будет рассуждать о золотой пропорции. О нем ведут шумные разговоры только гармонисты, пытающиеся свести все многообразие живой природе к единственной геометрической форме, которую они толком не представляют.

А что прикажете делать с этим многообразием форм? Они к чему стремятся?
*
* *Возьмите задачу о кроликах, предложенную Фибоначчи (рис. 8). Понятно, что кролики да и любые другие животные не размножаются строго в соответствии с известной числовой последовательностью 1, 1, 2, 3, 5, 8 и т.д. Математика вообще имеет дело только с идеальными случаями, не встречающимися в природе. Однако числа Фибоначчи неожиданно появляются в упаковках зерен сосновой шишки (рис. 9а), семена подсолнуха (рис. 9b) и маргаритки (рис. 9c), причем располагаются они по левым и правым взаимно ортогональным спиралям, число которых как раз совпадает с числами Фибоначчи. На рис. 9 приведены идеальные упаковки, вычерченные компьютером. Реальная шишка (рис. 10), подсолнух (рис. 11) и маргаритка (рис. 12) такого правильного строения уже не имеют. Кроме того, сами числа Фибоначчи, особенно начальные, слабо связаны с золотой пропорцией.

Рис. 8. Задача Фибоначчи о размножении кроликов. Некто поместил пару кроликов в некоторое место, огороженное со всех сторон стенками, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения.
а  b
b  c
c 
Рис. 9. Задача о кроликах порождает числовой ряд Фибоначчи, члены которого редко, но все же встречаются в окружающей нас природе. Например, зерна сосновой шишки (а), семена подсолнуха (b) и маргаритки (c) располагаются по левым и правым взаимно ортогональным спиралям, число которых совпадает с числами Фибоначчи.

Рис. 10. Сосновые шишки могут быть «левыми», если число ветвей у левой спирали больше, чем число ветвей у правой спирали, или, соответственно, «правыми». В нашем случае имеется 8 правых ветвей спирали (от центра на периферию по часовой стрелке) и 13 левых ветвей спирали (от центра на периферию против часовой стрелки), следовательно, данная шишка является «левой». Можно подсчитать, в каждой из 8 ветвей, принадлежащих правой спирали, находится по 13 зерен (за первое зерно принимается макушка шишки); и, наоборот, в каждой из 13 ветвей, принадлежащих левой спирали, находится по 8 зерен (у некоторых ветвей 8-е зерно либо отсутствует, либо является дефектным). Если строение шишки считать идеальным, то общее число ее зерен можно рассчитать двумя способами: 1) 13 · 7 + 1 = 92, 2) 8 · 12 + 1 = 97. Это расхождение неминуемо ведет к хаосу.

Рис. 11. Семена подсолнуха образуют структуру из трех систем спиралей, ветви которых удовлетворяют равенству 55 = 21 + 34. Наиболее отчетливо прослеживаются 34 ветви спирали правой закрутки. Ближе к центру имеется 21 ветвь и на периферии 55 ветвей еще двух спиралей, но уже левой закрутки. Так как число ветвей правой закрутки равно 34, а левой — 76, то этот подсолнух можно считать «левым». Число семечек (семян) в нем подсчитать сложнее, чем число зерен в сосновой шишке. Во всех 34 ветвях правой закрутки отчетливо видно, по крайней мере, 13 зерен. Следовательно, число семян равно 442. К этому числу ближайшими числами Фибоначчи являются 337 и 610. Что касается золотой пропорции, то о ней здесь можно вообще не вспоминать.

Рис. 12. У маргаритки число ветвей, закрученных по часовой стрелке, равно 24, а против часов — 34, следовательно, она, как и подсолнух с шишкой, относится к левосторонним объектам. Может быть, в соответствии с действием силы Кориолиса, в южном полушарии Земли маргаритки, подсолнухи и шишки имеют преимущественно правостороннюю закрутку? Интересно проверить, так ли это. Ведь должна же быть какая-то материальная причина, влияющая на преобладающую закрутку ветвей спиралей. Разве можно допустить, что закруткой управляет Господь Бог.
Итак, никакого золотого сечения в природе нет. С этим согласен как будто бы и сам Василенко, написавший: «безупречная математическая конструкция золотой пропорции в природе идеально себя не показывает» [24]. Другой бы сказал: нет так нет и махнул бы рукой, но только не фанатичный гармонист. Его вера в божественную гармонию столь велика, что он начинает придумывать хитроумные объяснения, почему нет золотой пропорции. В связи с этим процитирую концовку следующей статьи Василенко, опубликованной на сайте «Академии Тринитаризма» 17 мая 2009 года.
Он пишет: «Практически все, что о нем написано [о ЗС], сводится к двум простым вещам: либо к его асимптотически-ограниченным проявлениям (филлотаксис, строение подсолнухов, геометрия раковин и т.п.), по которым отсутствуют какие-либо доказательства о сколь-угодно длительном продолжении "золотых" тенденций в их последующем развитии; либо к оценочно-приближенным вычислениям разнообразных структурно-функциональных соотношений, которые квалифицируются как близкие к ЗС, иногда больше на веру.
Различные так называемые "обобщения золотого сечения" здесь не в счет, поскольку это издержки некорректной терминологии: они обобщают не само ЗС (константы не обобщаются!), а развивают общую теорию пропорций на совершенно другой основе, уже без свойств числа Ф. …
Создается такое впечатление, что, закручивая многие процессы и явления вокруг ЗС, движитель Вселенной, тем не менее, не впускает их развитие в непосредственную близость к числу Ф. Будто существует некая запретная граница, дальше которой подход к нему становится в буквальном смысле небезопасным для объекта. А причина представляется в том, что самое иррациональное и одновременно самое изящное сечение своей идеальностью не оставляет места наличию внутрисистемных связей, становясь фактическим разрушителем системы.
Да и сама Вселенная, как только в своих макро- или микро-проявлениях выйдет точно на ЗС (или приблизится к нему ближе некоторого минимально допустимого значения), видимо, запрограммирована рассыпаться и прекратить свое существование в современном представлении. Все превратится в Канторову пыль или бессвязный и бессистемный фрактал.
Число Ф в своем идеальном значении хотя и "золотое, божественное", но по своему внутреннему устройству, если так можно выразиться, в идеале имеет совершенно иную высшую цель, являясь носителем тления и распада, как в выражении "страшно красивая".
Это не вердикт или обвинительное заключение ЗС, это скорее Ода истинному ее величию, которая позволит нам по-новому заглянуть в глубину "структурной гармонии систем" (Э.М. Сороко) с надеждой на получение новых знаний и понимание подлинного смысла "кодов золотой пропорции" (А.П. Стахов).
Распределения с "тяжелыми хвостами", к которым относится и распределение Парето, являются чрезвычайно полезным инструментарием для исследования процессов, на первый взгляд, мало похожих или плохо вписывающихся в понятие гармонии.
Весь смысл заключается, что мы вкладываем в это понятие. Если гармонию мира, то все становится на свои места, поскольку его разнообразие включает в себя и проявление экстремальных редких явлений (катастроф, вулканов, рождения новых звезд и др.).
Гармония мира — это не только идиллия и согласованность красивых форм, присущих золотой пропорции. Гармония мироздания — это, прежде всего, многообразие форм в их единстве, когда могут присутствовать самые разные пространственные конфигурации и протекать различные временные процессы. Даже если они носят спорадический и нерегулярный характер, то все равно остаются частями целого.
Более того, их мощь в отдельные моменты может быть настолько сильной, что идеально гармоничные формы, выстроенные эволюцией, просто разрушаются, а на их восстановление (обновление) потом могут уходить целые эпохи» [24].
Я не знаю, ходит ли Василенко в церковь, но поскольку он предполагает наличие «движителя Вселенной», ему бы нужно ее посещать. Там, где у православных верующих стоят Иисус Христос и Матерь Божья, у гармонистов-золотоискателей стоят Гармония и Золотое Сечение — им они поклоняются как первичным, сверху спущенным принципам. Таким образом, их учение о Гармонии и Золотом Сечении есть своеобразная форма теологии, наподобие той, которую Готфрид Вильгельм Лейбниц представил прусской принцессе Софии-Шарлотте в своем сочинении «Теодицея».
Статья [24] посвящена математическим аспектам распределения Парето, но эта узкая тема отступает на второй план перед поднятой автором религиозной проблемой предустановленной гармонии. Оказывается, когда природа подходит к Золотому Сечению, своему божественному пределу, процесс неожиданно взрывается, гармония оборачивается катастрофой и число Ф становится недоступным.
Я окидываю взором отсканированные мной формы раковин аммонитов. Интересно, на какой из них природа подошла к своему Ф-пределу, за которым последовал взрыв? Нет такой раковины! Василенко рассуждает отвлеченно, не опираясь на какие-либо естественнонаучные данные по раковинам, шишкам, подсолнухам и прочим объектам. Он видит, что золотого сечения в природе маловато, все приводимые примеры сильно хромают. Чтобы не закапывать в землю свою веру в Гармонию, гармонист придумывает странную философию, в которой хаос объявлен вершиной гармонии, т.е. Бог превращается в дьявола.
Всеобщая Гармония Мироздания по Василенко
Сосредоточившись на разработке своей философской концепции ЗС и Гармонии, Василенко не упускал из виду и своих коллег-гармонистов. Ему показалось, что они явно перебарщивали с универсальностью и божественностью математических конструкций, которые этого не заслуживали. Стахов и его верные последователи придумали такие математические теории, в которых золотое сечение скорее «размазывалось», теряло позолоту, чем обобщилось и возвышалось, говорил критик.
«У нас же налицо своеобразный "демон ЗС" как символ всепроникающего нахождения, вездесущности и бесконечного присутствия, который способен в одночасье "проглотить" всю числовую ось или заполнить собой все мировое пространство. Но одно дело яркий слоган или брэнд, и другое дело — научное понятие. То есть, имеем явную несовместимость качественных характеристик в одном термине, что не позволяет однозначно выразить только одно понятие. Скорее всего, приходится "жертвовать" словом "золотое". Оно и логично. Не может же произвольное сечение (на две части) называться золотым, которому в математике уже давно отведено свое особое место. Сначала выделили ЗС, теперь же его выкручиваем и обобщаем, а вместо однозначной идентификации получаем "размывание и размазывание" термина» [25].
Василенко всё настойчивее и настойчивее, несмотря на растущее недовольство Стахова, подчеркивает мысль, что ЗС обобщить нельзя, поскольку предел один, так что сам термин «обобщение» не поддается осмыслению. Данное понятие вводит в заблуждение и тормозит нормальное развитие математической теории золотой пропорции и чисел Фибоначчи. По всему видно, что критик хочет честно разобраться не только в понятии «обобщенного ЗС», но идет дальше, пытаясь осмыслить, что создали его коллеги под вывесками чисел Трибоначчи, p- и pk-сечений, так называемых металлических пропорций и т.д. Он, как блюститель чистоты золотой религии, восстал против расширительного толкования их гармонического Бога.
Василенко пишет возмущенно: «Человек выбрал (особо выделил) одну единственную пропорцию, заслуженно посадил ее на трон, надел корону, назвал золотой и даже ассоциативно сравнил ее с Богом. Нет мало, теперь давай натягивать на нее фуфайку, а вслед за этим завтра вздумается примерить бескозырку. Потом уравняем с другими числами, объявим новые "золотые" сечения как производные и т.п. Полная нивелировка и подмена понятий, — иначе не назовешь. Так же как и, на первый взгляд, безобидные термины вроде бронзовой, медной и другой подобной пропорции (уже скоро таблицы Менделеева не хватит) … Кто может показать хоть одну маленькую крупицу этого-самого золота с малейшими признаками числа Ф? Право же, это похоже на алхимию (в хорошем смысле), — не получили золота, зато сколько новых химических элементов открыли» [25].
Однако 6 июня 2009 года выходит статья, свидетельствующая о резком изменении взглядов Василенко в отношении обобщенного золотого сечения. Это произошло под влиянием открытия им нового уравнения, которое по «обобщению» намного превосходила «обобщенное уравнение» Стахова. В коротком введении Василенко оправдывался, что его прошлая критика обобщения «вовсе не означает, что самому понятию «обобщение» не остается места в сфере отношений, регулируемых или вытекающих из свойств золотого сечения. Все зависит от контекста, логичности формулировок, отсутствия возможных терминологических противоречий (нестыковок), а также понимания или восприимчивости нововведений широкой научной общественностью» [13].
Это — просто слова, которые не способны были скрыть изменившуюся на 180 градусов позицию автора. В статье [13] Василенко представил «обобщенное уравнение гармонической пропорции» или золотого сечения. В подразделе «Анализ предшествующих изысканий» он критически оценил работу [14], в которой приведено обобщенное уравнение Стахова
xm = Fm x + Fm – 1 (1)
где Fm — числа Фибоначчи, (F1, F2) = (1,1).
Василенко проанализировал уравнение (1) и отметил его недостатки:
«1. При четном m оно имеет пару действительных корней (–φ, Φ), при нечетных значениях m к ним добавляется еще один отрицательный корень: –Φ < x3 ≤ –1, которому трудно придать физический смысл или интерпретацию с точки зрения золотого сечения.
2. Остальные корни — комплексные, которые при степенях m ≥ 6 не имеют аналитического представления, что не позволяет получить соответствующие формульные соотношения для тех или иных переменных, основанных на знании всех корней алгебраического уравнения.
3. Сходимость адекватных числовых последовательностей вида
к асимптоте Φ в общем случае обеспечивается только для малых величин m и наоборот очень большого удаления n от начальной точки (рис. 1).
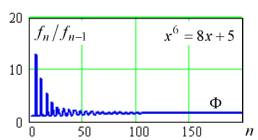
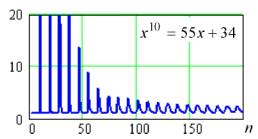
Рис. 1. Сходимость рекуррентных числовых последовательностей fn к асимптоте Φ, генерируемых алгебраическим уравнением (1) А.П. Стахова.
Таким образом, сама по себе хорошая идея [14] расширения класса алгебраических уравнений со свойствами золотой пропорции при ее реализации в общем виде (с использованием в качестве коэффициентов чисел Фибоначчи) натыкается на трудно преодолимые препятствия, и в результате становится малопродуктивной.
Дополнительный анализ показывает, что описанные признаки являются следствием большого разрыва между степенями членов уравнения, приводя к весьма слабой сходимости, как в подобных численных задачах нахождения экстремумов функции.
Вероятно, именно мера удаленности степеней уравнения лежит в основе интересных свойств и практических приложений p-сечений Стахова, построенных согласно уравнению
x p + 1 = x p + 1
с парой соседних целочисленных степеней x p + 1, x p.
Можно, конечно, в качестве затравочных элементов в (1) положить m чисел Фибоначчи, но тогда уравнение (1) генерирует сам ряд Фибоначчи, что лишено дополнительной смысловой нагрузки и не дает ключ к получению новых знаний» [13].
Эти недостатки уравнения Стахова (1) подвигли Василенко на свой вариант обобщения. В подразделе «Синтез обобщенного уравнения и его решение» он предложил следующее.
«Взяв за отправной посыл возможность тожественных преобразований ЗС, что естественным образом вытекает из уникальных свойств числа Φ, трансформируем логическую схему рассуждений.
В качестве исходного рассмотрим известное тождество ЗС:
Φ² = Φ + 1.
Умножив его поочередно m раз на Φ², после элементарных преобразований получаем:
(2)
Соотношение (2) есть не что иное, как запись уравнения через уже известное частное решение х = Φ.
Исходное алгебраическое уравнение, которое назовем обобщенным уравнением гармонической пропорции (ЗС), приобретает вид, m = 1, 2, 3,...
(3)
Например, «развернув» для наглядности знак-обозначение суммы, получаем

С учетом свойств мнимой единицы и числа е — основания натурального логарифма (в его связи с тригонометрическими функциями через уравнение Эйлера) легко убедиться, что обобщенное уравнение ЗС (3) имеет следующее аналитическое решение:
— действительные корни (для любого целого значения m):
(x1, x2) = (–φ, Φ);
— мнимые корни, которые идут четверками (m ≥ 3):
± exp (± ikπ/m), k = 1, ..., {(m – 1)/2}; (4)
— если m кратно 2, то к ним добавляются еще два мнимых корня: ± i, где i — мнимая единица» (здесь фигурные скобки {} обозначают взять целую часть).
Василенко обращает внимание на то, что его обобщенное уравнение при m = 1 дает уравнение x² – x – 1 = 0, а для произвольного m ≥ 1 имеет корень Φ. «Само ЗС, как уникальная математическая константа, никоем образом не обобщается, в том числе и уравнением (3)» [13].
«Главным математическим свойством всех уравнений типа (3) является то, — еще раз восторженно отмечает Василенко, — что для любого целого m ≥ 1 они имеют пару действительных корней (–φ, Φ) ЗС, как и для исходного квадратного уравнения (рис. 2)» [13].
В этом, мне кажется, нет ничего странного, если помнить, как было получено уравнение (3). Удивляет другое: как можно из уравнений (3) и (5) прийти к столь радужным надеждам, которые изложены под заголовком «Возможные направления дальнейшего развития и практического применения».
Относительно рекурсивного уравнения (5) Василенко пишет: «Обобщенное уравнение ЗС (3) порождает бесчисленное множество аддитивно-рекуррентных последовательностей в виде уравнения суммирующей V-рекурсии, n = 0, 1, 2, ...
 (5)
(5)
Последовательности (5) могут иметь сколь угодно много любых начальных условий, что обеспечивает дополнительные возможности для использования и расширения знаний в различных областях науки» [13].
*
* *Итак, получилось, что Василенко по степени обобщения уравнения ЗС намного перещеголял Стахова. Он как будто бы забыл, за что критиковал директора Института ЗС на позапрошлой неделе. Конечно, честнее было бы признаться и даже, возможно, извиниться за свою прежнюю позицию. Но наш критик ловко перепрыгнул через голову Стахова на противоположную сторону, и начал шельмовать его уже за недостаточную обобщенность обобщенного уравнения (1). Послушайте, до каких областей знаний «расширяют», по мнению Василенко, начальные условия формулы (5).
Он пишет: «"Золотое" сечение или гармоническая пропорция, которые описываются обобщенным уравнением ЗС (3) не столько что-то рассекают или гармонизируют, сколько в виде аттрактора объединяют и группируют своим "кодом" различные элементы в одно целое, что ближе к понятию синтеза.
А уже потом при анализе готовых структур мы можем наблюдать ее срезы как частное "зашумленное" проявление, почему и не имеет особого смысла гнаться за точностью демонстрирования свойств "золотого" сечения, особенно там, где его просто нет или оно подавлено шумами.
Уравнение (3) выводит на важное, многостороннее и действительно полезное обобщение (не только в общей концепции ЗС) об интегрирующем начале ЗС в развитии природных процессов и явлений. Робкие предположения, часто основанные на интуиции, а порой просто бездоказательные голословные утверждения о ключевой роли ЗС в мироздании теперь приобретают реальные очертания и выводят теорию ЗС из сферы догадок и гипотез в область построения более четкой и обоснованной теории.
Например, можно задать миллиарды–триллионы совершенно произвольных соразмерных начальных условий (целых, действительных, мнимых, иррациональных и др. чисел), и через считанное количество итерационных шагов рекурсия (5) выводит нас на ЗС с той или иной точностью.
Этот факт, по глубокой интуиции автора, имеет непреходящее значение, степень значимости которого сейчас еще трудно обозначить даже в первом приближении, а равенство-рекурсия (5) влечет за собой в неизведанную даль.
У понятия гармонической пропорции появляется "второе дыхание" и насыщенность настоящими гармониками (хотя и через комплексные переменные) в виде набора тригонометрических функций с различными, но строго организованными частотами.
Безликие числовые последовательности становятся прообразами конструирования и структурирования сложных природных образований, начиная с молекул, и заканчивая скоплениями галактик.
По такому принципу могли, например, сформироваться из газовых образований планеты и звезды, что позволит вплотную приблизиться к построению единой космологической модели, в которой физические законы отражают формы взаимодействия, а обобщенное уравнение ЗС – их внутренне (генетическое) содержание.
Бесконечно большое число парных взаимодействий, отражаемых уравнением (3), может пролить свет на причину или природу гравитации, в основе которой лежат не безликие гравитоны, а вполне осязаемые и уникальные математические свойства ЗС.
Наличие периодических гармоник (4) становится теоретическим подтверждением проявления ЗС в сердечных ритмах человека. Более того, эти гармоники позволяют смоделировать формирование таких небезопасных для человека резонансных процессов, как "разрыв сердца", "кровоизлияние в мозг" и др.
По мнению автора, одна из причин здесь кроется в преждевременно-ускоренном выходе организма на состояние, характеризуемое проявлением идеальных свойств числа Φ, что влечет за собой потерю системности цельных структур (кровеносных сосудов и др.), прежде всего, в их слабых местах…
Реализация концепции случайного формирования белков в "океанском бульоне" при дополнительном теоретическом обосновании может стать простой игрушкой. Поскольку не нужно бесконечно-случайного блуждания по комбинаторным сочетаниям типа "выйдет – не выйдет", а достаточно "знать код Φ", и тогда аддитивно-рекуррентный процесс (5) с безмерно большим количеством произвольных начальных условий (не равных одновременно нулю) автоматически выводит на нужный результат.
Кажущаяся, на первый взгляд, наивность евангельского сотворения мира приобретает реальные очертания: кто-то же должен был задать код ЗС, который с помощью суммирующей V-рекурсии способен за считанные шаги "объединить необъятное" в одно целое.
Теология получает обновленное и даже научно обоснованное понимание, а наука – дополнительный импульс развития (новую парадигму) и широкое поле исследований.
Для молодых ученых открывается необозримый простор для экспериментирования, поиска взаимосвязей и придания физического смысла новым закономерностям.
Обобщенное уравнение ЗС и адекватная ему V-рекурсия многое проясняют.
Так, число Φ немыслимо без своего "двойника" φ (на генетическом уровне), что проявляется не только в квадратичном характере исходного уравнения, но и его обобщении для любой четной степени 2m. То есть, налицо дуализм решения и триединое начало: целое и его двойственные, а в общем случае парные соотношения, что, в частности, повсеместно наблюдается в природе.
Это и есть один из основных законов "золотой" или гармонической пропорции.
Скорее всего, природа именно так и действует в своем развитии.
А красота, эстетичность форм и тому подобное, что обычно ассоциируют с "золотым" сечением, становятся всего лишь возможными экзогенными, не всегда устойчивыми проявлениями. Поэтому замечательные шишки, красивые подсолнухи или живописные раковины – это только первый слой (внешний налет) гармонической пропорции, который, что называется на виду, радуя глаз.
В решении уравнения (3) мы видим также присутствие других иррациональных и целых чисел (см. приложение), из чего следует, что в своем структурном конструировании число Φ не одиноко и как магнит-аттрактор притягивает через ЗС к себе другие числа, включая π, e, корни натуральных чисел и др.
Поэтому вовсе не обязательно искать какие-либо аналитические или точные зависимости-взаимосвязи для тех же констант Φ, π и e, которых, скорее всего, просто нет.
Но зато эти числа одновременно присутствуют в решении обобщенного уравнения ЗС, что, на наш взгляд, отражает их тесную взаимосвязь на уровне формирования и развития многих процессов Вселенной с ключевым аттрактором в виде ЗС, воссоздавая гармонию как единство, слаженность, согласованность и когерентность» [13].
Во, куда занесло парня! Читайте и перечитывайте этот фрагмент, в нем виден тот главный порок, которым страдают не только золотоискатели, но и все фантазеры-романтики, создающие ЕТВ — Единую Теорию Всего (эти три слова пишите с большой буквы, иначе кого-нибудь ненароком обидите). Я не устаю критиковать релятивистов за их наивное, но очень упрямое желание найти одно-единственное уравнение некоего суперполя многомерного гиперпространства, из которого бы вытекали все законы мироздания. Золотоискатели их превзошли на порядок по степени утопического сумасшествия. Их область притязаний воистину безгранична. Василенко удалось отыскать «генетический код Вселенной» [16]. Он таки придумал формулу бытия — обобщенное уравнение ЗС (3), — которую так долго ждало человечество. Теперь ему бы дружить семьями со Стаховым, высосавшему из пальца другую универсальную формулу — уравнение (1), — а они в ссоре. Почему так случилось, мы разберем позже, а сейчас хочу высказаться об одном недоразумении.
*
* *В статье, которую мы только что разбирали, я нашел следующее, на первый взгляд, не очень важное замечание, но на самом деле оно подведет нас к принципиальным вещам. «В работе [14], — пишет Василенко, — есть ссылка, что уравнение x4 = 3x + 2 описывает энергетическое состояние молекулы бутадиена — химического вещества, используемого при производстве каучука. Если там принципиально важны мнимые корни или вариабельность 4-х начальных условий, то это, безусловно, в пользу данного уравнения, если же нет, то вся нужная информация сосредоточена в обычном квадратном уравнении x² – x – 1 = 0» [13].
Стахов прокомментировал это место следующим образом: «Но обратимся к обобщенному уравнению гармонической пропорции
xm = Fm x + Fm – 1 , (1)
которое Василенко взял из моей статьи "Математика Гармонии как новое междисциплинарное направление современной науки" [14].
Заметим, что при m = 4 уравнение (1) принимает следующий вид:
x4 = 3x + 2. (2')
Уравнение (2') приводит нас к неожиданному результату, которое выходит за пределы математики. Оказывается, что уравнение (2') описывает энергетическое состояние молекулы бутадиена — ценного химического вещества, которое используется при производстве каучука. Известный американский физик, Лауреат Нобелевской Премии Ричард Фейнман выразил свое восхищение по поводу уравнения (2') в следующих словах: "Какие чудеса существуют в математике! Согласно моей теории, золотая пропорция древних греков дает минимальное энергетическое состояние молекулы бутадиена".
Этот факт сразу же повышает наш интерес к "золотым" алгебраическим уравнениям, задаваемым (1). Возможно, что именно эти уравнения могут быть использованы в качестве "золотых" математических моделей энергетических состояний молекул других физических веществ.
Именно эта цитата Ричарда Фейнмана меня очень заинтересовала и я начал изучать алгебраические уравнения типа (1), которые я назвал "золотыми" алгебраическими уравнениями. К этим исследованиям был привлечен мой ученик Борис Розин и результаты этих исследований были изложены в статье Stakhov, A., Rozin B. The "golden" algebraic equations. Chaos, Solitons & Fractals, 27(5) (2006), 1415-1421. Эта статья также опубликована на сайте «Академии Тринитаризма» в разделе "English content"... Я обращаю внимание всех читателей нашего сайта и особенно проф. Василенко на существование такого раздела на сайте «Академии Тринитаризма» и прошу познакомиться со всеми моими англоязычными статьями, опубликованными в этом разделе» [15].
Я когда-то занимался расчетом энергетических состояний кристаллов и отдельных молекул вроде бутадиена. Хочу заметить, что бутадиен, химическая формула которого выглядит как
CH2 = CH – CH = CH2,
имеет совершенно иное уравнение для нахождения собственных энергетических уровней, а именно:
= x4 – 3x2 + 1 = 0, (3')
= ±1.618, ±0.618.
Как составляется матрица смежности химического соединения, рассказывается в разделе Матрицы смежности и линейчатые спектры. Замечу, только характеристическое уравнение (3') дает корни φ и Φ, но оно сильно отличающееся от уравнения (2'), которым восхитился Фейнман, а за ним Стахов и, наверное, Василенко. Я не взваливаю вину за эту ошибку на Стахова или Фейнмана, считая, что здесь имело место какое-то недоразумение. Но важно помнить, что обобщенное уравнение Стахова (1) не приводит к истинному уравнению (3') для нахождения линейчатого спектра молекулы бутадиена.
В конце концов, и на этот прискорбный для Стахова факт закроем глаза. Предположим на минутку, что уравнение (1) всё-таки приводит к уравнению (3'). Сейчас важно будет обратить внимание на ложные маяки, освещающие путь золотоискателям в их поисках сокровищ.
Подумаешь, бутадиен! В природе существует миллионы соединений, мультиплеты которых и близко не дают числа φ и Φ. Так, например, в указанном выше подразделе «Конструктивной математики» приводятся энергетические уровни фуллерена, а также тетраэдрических и додекаэдрических соединений. Всё это — идеальные модели, их реальные спектры слегка, а бывает довольно заметно, отличаются от «золотых» значений. И вот, одно из многих углеводородных соединений дает близкие к ним величины. И что же, бутадиен нужен нам как талая вода для Белянина? Отнюдь, без него легко можно прожить и здоровяку Белянину и всем нам, хилым и убогим.
Верно, что он легко полимеризуется и поэтому применяется для производства синтетических каучуков. Но для производства самого бутадиена используются бутены (C4H8) и бутаны (C4H10), которые, между прочим, применяются для получения гораздо более широкого класса веществ: прежде всего, самого бутадиена, затем, ацетальдегида, изооктана, различных масел, моторного топлива и т.д. Однако энергетический спектр этих двух более фундаментальных углеводородов не дает значения 1,618 и 0,618. Бутадиен часто приводят в качестве показательного примера именно из-за этих двух золотых чисел как некий уникум среди множества рядовых веществ.
Что касается Ричарда Фейнмана, то он, как и Роджер Пенроуз, любил создавать шум вокруг рядовых фактов, почему и прославился среди экзальтированных физиков. Думаю, по наводке Фейнмана Стахов перерыл множество книг в надежде напасть на след золотой пропорции в области химических соединений. Естественно, его ожидало горькое разочарование, но он нам об этом не говорит, пытаясь прикрыться одним-единственным веществом, бутадиеном, делая его особо «ценным» в наших глазах.
Как поссорились Сергей Леонидович с Алексеем Петровичем
В одном из своих выступлений на сайте «Академии Тринитаризма» Василенко вдруг, без особых на то причин, решил рассказать, как он попал в компанию гармонистов-золотоискателей Стаховского призыва. «С «Академией Тринитаризма» я встретился благодаря триалектике [расширенная диалектика] и работам П.Я. Сергиенко, Р.Г. Баранцева и др., когда решил воплотить старые задумки на тему: "И да, и нет", — как третьего состояния, которое также сродни "Ни да, ни нет". Здесь и нечеткие множества, и пограничные состояния, учение о троице и т.д.
Начал собирать материалы (с уклоном в экологию и знаний о воде), наткнулся на триалектику и стал ее штудировать. Позже на сайте мое внимание привлек "Институт ЗС", вспомнил юность, когда еще в школе самостоятельно изучал пирамиды, бином Ньютона, метод индукции, — так и переключился на золотое сечение.
С большим удовольствием перечитал многие работы. Особенно поразило то воодушевление, с каким ученые, инженеры и специалисты самых разных направлений активно вели поиски и с упоением обсуждали, на первый взгляд, незамысловатую пропорцию — едва различимую на общем фоне человеческих знаний.
Нашлись люди, которые до сих пор в г. Харькове тепло отзываются и помнят Алексея Петровича Стахова. Это придало мне дополнительную энергию, чувство сопереживания и сопричастности к идеям золотой пропорции, которые благодаря его неукротимой энергии и энтузиазму витали в нашем городе в 70-е годы» [26].
Три десятка лет Сергей Леонидович работает на Харьковском водопроводе. В 1998 году защитил кандидатскую диссертацию по теме «Статистическое моделирование качества воды в водотоках», а в 2007 — докторскую по теме «Экологическая безопасность систем водоснабжения городов». Первая статья, связанная с проблемами Гармонии, Золотого Сечения и чисел Фибоначчи, появилась на сайте «Академии Тринитаризма» 27 марта 2008 года. После опубликования 23 февраля 2009 года седьмой статьи на данную тему Стахов подвел черту под его творчеством.
В своем «Отклике на публикации С.В. Василенко» директор Института ЗС, ошибаясь в инициалах, писал: «С.В. Василенко обладает достаточной математической культурой — и с математической точки зрения никак претензий у меня не имеется. Я приветствую появление в нашей среде яркого исследователя, обладающего высокой математической культурой, но при этом хочу сделать одно замечание. К сожалению, большинство публикаций С.В. Василенко являются по существу повторением того, что уже сделано в этой области» [18].
Далее Стахов подробно разъяснил, в чем заключаются повторения. Нам с вами, дорогой читатель, будет трудно разобраться в этих деталях без соответствующих предварительных знаний. Боюсь, что статья [18] с самого начала писалась только для одного читателя по фамилии Василенко, которого там критикуют, никто посторонний в ней ничего не поймет. Тем не менее, чтобы оценить степень неприязненных отношений между нашими спорщиками, возникших при первом же письменном контакте, пустим пунктиром несколько характерных фраз из указанной статьи.
Стахов пишет: «В статье […] Василенко попытался "параметризировать" симметричные гиперболические функции Фибоначчи и Люка, введенные в статье Стахова и Розина в 2004 г. […]. Следует отметить, что задолго до него "золотые" параметризированные гиперболические функции были введены Олегом Боднаром в его статье […], опубликованной в 1992 г. В своей статье […] я изложил критические замечания в адрес [Василенко] … [Там] я отметил, что в области "золотых" гиперболических функций (или гиперболических функций Фибоначчи и Люка) есть две пионерные публикации. Это — статья Боднара […] (1992 г.) и статья Стахова и Ткаченко […] (1993 г.) … Дальнейшее обобщение идеи симметричных гиперболических функций Фибоначчи и Люка дано в статье Стахова … 2006 г. … Странно, что в статье С.В. Василенко […], посвященной изложению "золотых" гиперболических функций, основанных на "металлических пропорциях" Веры Шпинадель, нет ссылки на статью [Стахова]. …
Теперь несколько слов о других статьях Василенко […], в которых он делает обобщения чисел Фибоначчи. Дело в том, что подобного рода обобщения уже сделаны в работах […], опубликованных мною в международном журнале "Chaos, Soltons and Fractals" (Англия) в соавторстве с [иностранными товарищами]. Например, в работе […] дано так называемое q-расширение p-чисел Фибоначчи и Люка … А это, по существу, тот же результат, на который претендует С.В. Василенко в статье […].
Подводя итог критическому анализу работ С.В. Василенко, я хотел бы сказать следующее. Я далек от обвинений С.В. Василенко в плагиате и считаю, что все исследования, изложенные в работах […], выполнены С.В. Василенко самостоятельно. Хотелось бы отметить достаточно высокий математический уровень работ С.В. Василенко. Однако я рекомендую С.В. Василенко, приступая к исследованиям в этой области, внимательно ознакомиться со всеми публикациями в области золотого сечения как в русскоязычной, так и англоязычной литературе. Это позволит избежать "ляпсусов", на которые я обратил внимание в этой статье. … И я очень просил бы проф. С.В. Василенко не обижаться на меня за критические замечания, изложенные в настоящей заметке» [18].
Как видим, обвинение в плагиате здесь не предъявлено, более того, особо подчеркивается, что вся работа автора […] проделана самостоятельно. На эти внятно сформулированные замечания директора Института ЗС Василенко никак не отреагировал. Мне трудно сказать почему. Возможно, потому, что Василенко чувствовал свою вину, возможно, причина была совершенно иной. Если он станет оправдываться, существует вероятность того, что его лишат права публиковаться на сайте «Академии Тринитаризма». Так или иначе, но после стаховской критики Василенко более месяца ничего не публиковал, что по его меркам долго, ибо автор он чрезвычайно плодовитый.
Зато в апреле появилось сразу четыре его статьи. В первых трех (от 9, 14 и 23 апреля 2009 года) Василенко рассуждал на темы, далекие от тех, за которые его критиковал директор, а в четвертой статье (от 25 апреля) он поднял проблему, положительное решение которой автоматически снимало с него обвинения в повторении чужих идей. Проблема эта связана была с «обобщением ЗС», предложенным Стаховым еще в далекие 1970-е годы и подхваченным его единомышленниками.
В статье [19] Василенко провозгласил: есть только одно золотое сечение, выраженное в конкретных числах 1,618… и 0,618…; каких-то других золотых сечений, в том числе «обобщенных», быть не может. И хотя к золотоискателям обобщенного ЗС критик причислил и себя, фактически, это его заявление означало, что Стахов, Ткаченко, Боднар и др. на протяжении многих лет занимались ерундой. В подразделе «Об одной "условной асимптотике"» Василенко написал: «Речь идет о так называемых обобщениях ЗС, к которым "приложил руку" и сам автор. Это металлические пропорции, p-сечения А.П. Стахова, многофункциональное обобщение С.Л. Василенко и др.
Непредвзятый простой анализ показывает, что подобные обобщения ЗС на самом деле ничего не обобщают, но в своем частном проявлении могут вырождаться в гармоническую пропорцию. Они представляют самостоятельные группы (классы) пропорций, возможно, даже очень важные, но не имеющие ничего общего с ЗС, кроме того, что являются корнями алгебраических уравнений, одним из которых описывается и ЗС.
ЗС уже уникально в своих проявлениях, и обобщить его как-то дальше невозможно. Можно развивать и расширять сферу и разнообразие математических соотношений целого и его частей. Но ЗС останется во всем этом безбрежном море-множестве уникальным островком — своеобразным аттрактором и центром притяжения других пропорций. Именно это важно и является главным. А так кладутся "в одну корзину" бесконечные множества разных последовательностей без какого-либо практического приложения.
Даже если какое-то новое алгебраическое уравнение неожиданно находит применение в конкретной области науки, то это не повод увязывать его с ЗС только на том основании, что и ЗС — это корень квадратного уравнения. Поэтому использование термина "обобщенное золотое сечение" в любом его проявлении следует признать неудачным.
На наш взгляд это стало естественным следствием большого желания ряда исследователей (автор относит и себя к их числу) как-то расширить математическую сферу ЗС. Слишком уж несопоставимо ассоциируется обоснованная претензия ЗС занять центральное место в математической гармонии мироздания со сравнительной скудностью его математических свойств, хотя воистину фундаментально-уникальных.
Можно показать, что практически любое алгебраическое уравнение произвольной степени с хорошо подобранными коэффициентами является генератором рекуррентных последовательностей, в которых отношение соседних членов стремится к максимальному действительному корню этих уравнений. Эти последовательности допустимо называть расширением классического ряда Фибоначчи, находить в них свои закономерности, строить разные зависимости. Но это другая систематика, иные соотношения, и ЗС здесь ни при чем.
Например, корень из двух — это корень из двух, но никак ни обобщение ЗС. "Одни трамвай зеленый, а другой свернул за поворот" — это и есть суть всех наших обобщений ЗС.
Можно также говорить о математической теории пропорций или соотношений целого и его частей, и ЗС в этой теории — весьма значимый, но всего лишь частный случай.
Более того, обсуждая классическую тему соотношения целого и его элементов, еще великий Аристотель акцентировал внимание на том, что "целое больше суммы своих частей". Но даже ЗС в чистом виде этого не дает. Тогда где же та дельта, которая характеризует именно то в целом, чего нет у его составных элементов?
Одно из решений подобной задачи при рассмотрении ЗС предлагал в свое время И.А. Марутаев […]. Но выглядело это несколько искусственно из-за его большого стремления напрямую увязать ЗС с постоянной тонкой структуры α.
Со временем физики изменили ее значение в сторону уточнения, и все авторские выкладки и погоня за тождественностью оказались сомнительными. Тем не менее, предложенная им идея учета системных связей в целом, описываемым характеристическим уравнением ЗС, остается важной и сегодня» [19].
Стахов на эту критику отреагировал мгновенно. Уже на следующий день, 26 апреля 2009 года, появилась его заметка, в которой он, как настоящий гуру, убедил «читателей в ошибочности предложения Василенко упразднить сам термин "обобщенные золотые сечения" и не применять его в научной практике ЗС.
Исследования в области обобщений чисел Фибоначчи и золотого сечения являются важным направлением развития современной теории ЗС и они могут привести к новым научным открытиям.
По-моему, нужно уважительно относиться к современной истории ЗС, работам своих предшественников, без которых не было бы и работ С.Л Василенко, и не пытаться выступать в роли некоторого "гуру" в этой области, осуществляя ревизию основополагающих результатов» [20].
Сколько физиков справедливо заявляло, что название «Общая теория относительности» не подходит к ней. Однако право называть теорию так или иначе принадлежит ее создателю. Кроме того, спор о словах — это всегда спор не совсем по существу. В нашем случае ситуация усугубляется еще и тем, что Василенко менял свое отношение к обобщению уравнения ЗС ровно на противоположное (см. предыдущий подраздел). Делал он это, исходя из математических и философских соображений, которые, однако, не отличались большим постоянством. Так что всё сказанное им здесь он впоследствии перечеркнет своим суперобобщением, так что стаховское замечание по поводу того, чтобы критик более уважительно и внимательно отнесся к тому, что сделали его предшественники в течение многих лет, выглядит вполне резонно.
*
* *Следующей публикации, появившейся на сайте «Академии Тринитаризма» 8 мая 2009 года, Василенко предпослал поздравление своему оппоненту: «К 70-летию профессора, д.т.н. Стахова А.П. с пожеланием ему крепкого здоровья и воплощения в жизнь всех творческих задумок и начинаний по развитию золотого сечения в современной науке». Содержание этой статьи в пику разговорам о проблемах общения ЗС касалось частной проблемы рационализации ЗС. Разбором ее содержания мы занимались в подразделе От РЗС Василенко к раковине Nautilus pompilius. Заканчивалась статья [21] тоже добрыми пожеланиями в адрес именинника: «долгоденствия и долголетия, как в числах Фибоначчи в их нескончаемом движении к "золотому" сечению, хочется больше всего пожелать уважаемому юбиляру и прославленному "золотоискателю" — Стахову Алексею Петровичу!»
Право поздравлять юбиляра принадлежит родным, близким друзьям и президентам. Василенко не проходит ни по одной из этих категорий. Ему бы лучше воздержаться от подобных посланий, иначе это выглядит как лицемерное угодничество. Уверен, Стахов даже при своей слабости к лести, испытал неприятное чувство, когда увидел поздравление от своего язвительного критика.
17 Мая Василенко опубликовал статью [24], содержание которой мы выше уже касались. В ней тоже не наблюдается следов критики; напротив, есть два легких почтительных кивка в сторону Стахова и Сороко. А вот следующая статья [27], опубликованная на сайте «Академии Тринитаризма» 19 мая, вызвала уже критику в обратном направлении, от директора Института ЗС в адрес Василенко.
«Мое главное замечание, — пишет Стахов, — состоит в том, что проф. С.Л. Василенко недостаточно знаком с западной математической литературой по теории чисел Фибоначчи. Дело в том, что "золотые" ряды Фибоначчи с произвольными начальными условиями весьма детально исследованы в книге Vajda, S. Fibonacci & Lucas Numbers, and the Golden Section. Theory and Applications. Ellis Horwood limited (1989), которая является одной из лучших англоязычных книг в этой области. Подавляющее количество соотношений, которые проф. Василенко выдает за оригинальные, описаны в этой книге, что снижает научную ценность статьи Василенко. Отсутствие ссылки на эту широко известную книгу у меня вызывает большое удивление» [28].
Это обвинение уже тянет на плагиат, но этого страшного слова Стахов пока не написал. Он всё еще сохраняет хладнокровие и, в соответствии со своим высоким статусом директора Института ЗС, назидательно советует: «В заключение я хотел бы подчеркнуть, что все направления в этой области, которые приводят к новым и непредсказуемым результатам, можно только приветствовать. Но первый шаг любого серьезного исследователя состоит в том, чтобы тщательно изучить все, что сделано его предшественниками. Я считаю, что без предварительного изучения таких математических книг, изданных в западной литературе, как [идет перечисление] вряд ли стоит публиковать какие-либо результаты в этой области. Это рано или поздно приведет к недоразумению или открытию уже исследованного» [28].
Далее выходит статья [25] (28.05.2009), с которой начался подраздел Всеобщая Гармония Мироздания по Василенко. В нем говорилось, что камнем преткновения в споре между Стаховым и Василенко сначала послужила проблема обобщения уравнения ЗС. Потом трещина взаимных упреков поползла по другим темам. Раньше обращалось внимание главным образом на философию гармонии и золотой пропорции, исповедуемую Василенко, сейчас наше внимание сосредоточено на развитии конфликта между ним и Стаховым. В этой связи приведем из статьи [25] еще несколько фрагментов.
Во введении Василенко признает, что его прежние статьи [19] (25.04.2009) и [27] (19.05.2009) страдают «фрагментарностью» и, «порой, излишней эмоциональностью», а это послужило причиной критики Стахова [20] (26.04.2009) и [28] (20.05.2009). Он также отметил, что «Академия Тринитаризма и Институт Золотого Сечения, чтобы и где ни говорили, по праву занимают одно из ведущих мест по разработке и популяризации идей в выбранном направлении, так же как неоспоримы личные заслуги в этом А.П. Стахова, В.Ю Татура и др.» [25].
Эти примирительные настроения не долго удерживали критика от привычной для него язвительной манеры. В середине статьи, когда полемический задор разгорелся в полную силу, Василенко припомнил всё своему оппоненту. «"Золотых пропорций существует бесконечное количество", — утверждает А.П. Стахов [14], вводя себя в иллюзию, а своих учеников и последователей сбивая с толку.
Не золотых, уважаемый Алексей Павлович, а вообще пропорциональных зависимостей действительно существует бесконечное множество, среди которых те же р-сечения по праву занимают достойное место, и никто с этим не спорит. Но "золотая" пропорция — все-таки одна! Это только ее знак качества и отличительный признак (код). Но это не разменное клеймо, которое можно ставить на все подряд, если есть действительное желание обустроить жилище ЗС и математики гармонии, очистив их от излишних и ненужных наслоений, с которыми нельзя выстроить "новое междисциплинарное направление современной науки"» [25].
В конце критик вышел из берегов своей статьи и в P.S. добавил: «По конструктивной критике в мой адрес со стороны профессора А.П. Стахова, прозвучавшей на страницах сайта «Академия Тринитаризма», хотелось бы высказать одно соображение в части расстановки "вешек-указателей", о которых говорилось выше. Для этого приведу слова Алексея Петровича: "По существу классическая теория чисел Фибоначчи полностью исчерпала себя после публикации книги проф. Vajda и введения гиперболических функций Фибоначчи и Люка (Стахов, Ткаченко, Розин)…" [4].
Получается, что капитан сказал: "Сушите весла". Не совсем ясно, что имеется в виду под словами "классическая теория чисел Фибоначчи", но в моем представлении данное направление только получает свое "второе дыхание", продолжая развитие и воплощение (пока еще вялое) в практику. И предавать его забвению, думается, преждевременно.
Для этого достаточно проанализировать литературу, например […], по обобщенным последовательностям Фибоначчи на основе арифметических, геометрических и комбинаторных свойств различных модификаций обобщенной пирамиды Паскаля с ее обширными и неизведанными возможностями компьютерной реализации и моделирования природных процессов.
Со своей стороны в развитие теории рационального ЗС на страницах "Академии Тринитаризма" с согласия администрации сайта планирую предложить молодым ученым и практикам концептуальную идею "Метода лечения злокачественных новообразований на основе чисел Фибоначчи". А вот на псевдообобщениях ЗС (не путать с развитием общей теории пропорции и гармонии) действительно нужно ставить точку, также как и на не научном термине "обобщенная золотая пропорция", который противоречит не только основным требованиям ИСО [Работа в области терминологии], но и логике многовекового развития ЗС. Для многих, это уже не гипотеза, а факт. Так что слово за первооткрывателем» [25].
Обращаясь к книге Вайды (Vajda), о которой говорилось в статье [28], ни Стахов, ни Василенко не уточняют, в чем именно произошло пересечение идей, читателю невозможно сориентироваться во взаимных упреках. Крайне любопытным местом в P.S. является предложение Василенко — пока что на уровне «концептуальной идеи» — «метода лечения злокачественных новообразований на основе чисел Фибоначчи». Что это? Может быть, главный гидролог Харьковского водопровода предлагает особую настойку на талой воде Белянина? Интересно, очень интересно, что придумал профессор-эколог.
*
* *Однако вернемся к теме обобщенного уравнения ЗС Стахова, идущего у нас под номером (1), и критики его Василенко, предложившего более обобщенное уравнение (3). И хотя критик в конце статьи [13] (06.06.2009) отвесил низкий поклон хозяевам сайта «Академии Тринитаризма», а в другой статье [16] (15.06.2009) назвал себя «одним из учеников-заочников» Стахова, война между гигантами золотой мысли развернулась не шуточная. В очередной «реплике» [15] (09.06.2009) Учитель начал с поглаживания по головке восставшего против него ученика-заочника.
«Мне понравилась статья проф. С.Л. Василенко..., — написал Стахов. — Я очень рад, что проф. С.Л. Василенко обратил внимание на …». Еще раз: «Но в целом статья проф. Василенко мне понравилась. Она является дальнейшим развитием теории "золотых" алгебраических уравнений, изложенных в статье Stakhov, A., Rozin… Очень интересны результаты, связанные с компьютерным моделированием этих уравнений. Очень приятно, что С.Л. Василенко очень тепло отзывается об английском математике проф. Vaida и ссылается на книгу Vaida, чего не было в его предыдущих публикациях. Приятно, что изменилась "тональность" высказываний С.Л. Василенко по поводу работ его предшественников, в частности, по поводу работ Эдуарда Сороко» [15].
Но местами похвально-слащавый тон Стахова становился горько-менторским: «Я обращаю внимание всех читателей нашего сайта и особенно проф. Василенко на …». «Я считаю, что отсутствие ссылки на статью Stakhov, A., Rozin B. … является существенным недостатком статьи С.Л. Василенко. Но я вижу, что проф. Василенко постепенно "исправляется" и я надеюсь, что в его последующих публикациях будут ссылки на работы его предшественников» [15].
Звучит всё это, конечно, неприятно, что вызвало раздраженную реакцию Василенко. Он отказался восседающему на золотом троне директору Института ЗС поклониться в пояс и поцеловать его золотой сапожок: «Профессор А.П. Стахов часто и по праву выступает как капитан и наставник "золотоискателей". Частенько и в роли назидателя, нравоучителя или ментора. Но, да простят меня многие, беспардонность, с какой он нередко комментирует чужие статьи, порой искажая смысл и принижая степень новизны ее авторов, не забывая при этом многократно повторять и "выпячивать" одни и те же собственные наработки, не может не вызывать, мягко говоря, удивления, и объяснимого в такой ситуации естественного человеческого раздражения и даже протеста». Больше того: «возникает чувство, что тебя обкрадывают, нивелируют и даже снисходительно, похлопывая по плечу, фактически принижают. Каждый человек в своей жизни хоть однажды встречался с подобными ситуациями, которые порождают неловкость, дискомфорт и другие неприятные ощущения» [16].
Затем, как и во многих других случаях, проблема закрутилась в основном вокруг двух обобщенных уравнений — Стахова (1) и Василенко (3). Во-первых, констатировал Василенко, уравнение (1) «никогда ранее не именовалось обобщенным уравнением гармонической пропорции. Сам ее автор, профессор А.П. Стахов, до сих пор всегда называл "золотым" алгебраическим уравнением (с коэффициентами в виде чисел Фибоначчи F ), пусть оно таковым и остается. Введенный в работе [13] термин обобщенного уравнения гармонической пропорции обозначает совершенно иную математическую конструкцию на принципиально новой основе. …
Во-вторых, я ничего здесь у проф. А. Стахова не взял (хотя и считаю себя одним из его учеников-заочников), но проводил, как и принято, анализ предшествующих работ, что есть две большие разницы. Более того, наглядно показано, что математически корректное введение чисел Фибоначчи непосредственно в уравнение ЗС на деле становится малопродуктивным, в том числе, и по сходимости результатов (рис. 1), что дает полное основание мыслить и рассуждать дальше в поисках новых идей и решений» [16].
В-третьих, «а почему, собственно, нужно указывать в библиографии бесчисленные произведения, в которых без конца повторяются одни и те же стаховские заслуги?» — так примерно подумал взбунтовавшийся ученик о своем Учителе. Но на экране монитора мы прочли более мягкую формулировку его дерзкой мысли: «приходится проанализировать статью А. Стахова и Б. Розина на предмет ее удовлетворения критериям работы, которую другие авторы считали бы за честь включить в список используемой литературы…» [16].
В-четвертых, Василенко возмутили слова Стахова о том, что статья [13] «является дальнейшим развитием теории "золотых" алгебраических уравнений (?), изложенных в статье Stakhov, A., Rozin B.». Он пишет гневно: «Здесь уже налицо полнейшее искажение и нивелировка А.П. Стаховым смысла и содержания работы [13] с алогичной подстройкой под его собственные (мало кому понятные) "обобщения золотого сечения". …
Представляется, что Алексей Петрович и сам превосходно понимает всю несуразицу своего обобщения (исключительно с точки зрения терминологии!!!), просто не хочет с этим расставаться, поскольку многочисленными публикациями ввел в иллюзию уже не один десяток читателей и своих последователей. В конце концов, если нравится или "нельзя, но сильно хочется", каждый вправе принимать собственное решение. Только незачем распространять свою идеологию и бесцеремонно наклеивать ее ярлыки на работы других авторов» [16].
Заключительный аккорд этой критической симфонии всё испортил. Василенко, испугавшись, что его прогонят с сайта «Академии Тринитаризма», стал целовать золотые сапожки директора Института ЗС и биться головой об пол. Он пишет заискивающе: «Несмотря на общую тональность данной статьи (местами, сам вижу, даже нервозную), хочется закончить ее на жизнеутверждающей ноте и принести профессору А.П. Стахову личную признательность за хорошо организованную школу золотого сечения, азы которой я постигал и по его работам, в том числе опубликованным в материалах Академии Тринитаризма. А это важнее всех споров и дискуссий, много стоит и не забывается ни при каких обстоятельствах» [16].
Мягкотелость бунтарей только бесит королей. Эта не к месту высказанная признательность, после стольких щелчков по носу, вызвала у Стахова чувство брезгливости и презрения. Он, разумеется, никогда не простит своего ученика-заочника, которого он, добрый и мудрый Учитель, так нахваливал, а тот у всех на виду облил его помоями. Ссора между ними приобрела еще более ядовитую и жаркую форму, хотя внешне всё выглядело пока вполне пристойно.
*
* *«Уважаемый Сергей Леонидович!
Извините опять за "менторский" тон. Я работаю в этой области более 40 лет. Я неплохо знаком, как с русскоязычной, так и англоязычной литературой по проблеме чисел Фибоначчи и золотого сечения. Со многими ведущими современными западными специалистами в этой области (Scott Olsen, Jay Kappraff, Vera Spinadel, El Nashie и др.) я нахожусь в e-mail-переписке и знаком со всеми их современными публикациями в этой области. Как активный автор статей по числам Фибоначчи, опубликованных в западных журналах (свыше 20 публикаций), я часто получаю статьи по числам Фибоначчи, посвященных развитию обобщенных чисел Фибоначчи и обобщенных золотых пропорций, с просьбой прорецензировать ту или иную статью. Кстати, я опубликовал 15 статей в журнале «Chaos, Solitons and Fractals” и эти публикации вызвали волну статей именно по обобщенным числам Фибоначчи и гиперболическим функциям Фибоначчи и Люка в этом журнале. Поэтому, как говорится, я — «в курсе дела», и мне достаточно одного взгляда на статью, чтобы определить — содержит ли она новую информацию и что в этой статье упущено. К сожалению, мои замечания не всем нравятся, в том числе и проф. Василенко. И он — не первый, кому я делаю замечания. Приведу некоторые примеры» [29].Первый пример касался работы 2005 года, Александра Татаренко, чьи идеи пересеклись с идеями статьи 1998 года аргентинского математика Веры Шпинадель (Vera W. de Spinadel). Она исследовала семейство квадратных уравнений, обнаружила «металлические пропорции» и нашла им применение. Эти ее идее пересеклись с идеями американского ученого Джея Каппраффа (J. Kappraff), который в 2001 и 2002 году написал две книге, пересланные затем Стахову. Каппрафф именовал «металлические пропорции» — «серебряными». Позже Стахов установил, что пропорции Шпинадель и Каппраффа имеют определенное сходство с «формулой Газале»; в 1999 году Мидхат Газале (Gazale) по этому поводу издал книгу. Когда Стахов сообщил об этом Татаренко, тот, естественно, расстроился, поскольку первым автором «математического открытия» оказался не он.
Следующий пример касался, собственно, «предложения Василенко о приведении гиперболических функций Фибоначчи и Люка к "стандартной форме"». Стахов «обратил внимание проф. Василенко на тот факт, что это уже сделано в работах львовского исследователя Олега Боднара. После этого в работах Василенко появились ссылки на работы Боднара, что свидетельствует о том, что с работами Боднара он до этого не был знаком.
Второе мое замечание касалось статьи проф. Василенко "Обобщенные "золотые" pk-пропорции", в которой он претендует на введение новых обобщенных золотых пропорций (любопытно, что в этой статье он употребил название "золотые" pk-пропорции, за что затем меня начал критиковать). В статье [3] я обратил его внимание, что подобные "обобщения" были сделаны в статье [29 October 2007], опубликованной в журнале “Chaos, Solitons and Fractals”. Я проинформировал о статье [29 October 2007] в своей статье [02.01.2008], опубликованной на нашем сайте.
Третье мое замечание касалось статьи проф. Василенко [17.02.2009]. В этой статье он претендовал на введение новых классов гиперболических миров природы, основанных на новых обобщениях золотой пропорции типа "металлических пропорций". В своем отклике на эту статью я обратил внимание Василенко, что нельзя публиковать подобную статью без ссылок на мою статью [15], в которой введены подобные же классы гиперболических функций.
Четвертое мое замечание касалось статьи Василенко [27] (19.05.2009), в которой он исследует "Золотые ряды" Фибоначчи с произвольными начальными условиями. В своей статье [28] (20.05.2009) я обратил внимание С.Л. Василенко на тот факт, что "Золотые ряды" Фибоначчи с произвольными начальными условиями подробно исследованы в книге проф. Вайды (Англия) [Fibonacci & Lucas Numbers …], опубликованной в 1989 г. В своих последующих публикациях проф. Василенко начал ссылаться на книгу Вайды, откуда я сделал вывод, что он об этой книге до этого не знал.
Наконец, мое последнее замечание касается статьи С.Л. Василенко [13] (06.06.2009), в которой он исследует обобщенное уравнение гармонической пропорции, корнем которого является "золотая пропорция". В своей статье [15] (09.06.2009) я обратил внимание проф. Василенко на то, что подобные уравнения, названные "золотыми" алгебраическими уравнениями были впервые исследованы в статье Стахова и Розина […], опубликованной в 2006 г. Однако, я хочу подтвердить, что в статье С.Л. Василенко [15] (09.06.2009) в развитие статьи [Stakhov A., Rozin B., 2006] получено ряд новых результатов в этой области.
Таким образом, на основе анализа упомянутых выше работ С.Л. Василенко, у меня сложилось следующее впечатление. Проф. Василенко начал активно внедряться в "теорию чисел Фибоначчи", не ознакомившись предварительно с работами других авторов в этой области. Юмористичность ситуации состояла в том, что в своих предыдущих работах я так или иначе касался тех же задач, которым были посвящены статьи проф. Василенко. В результате мне пришлось давать комментарии по поводу некоторых его статей, в которых он описывал результаты, полученные другими авторами. Тем не менее, я не сомневаюсь в том, что все результаты С.Л. Василенко получены им самостоятельно и все эти статьи написаны на высоком математическом уровне. И вообще я считаю проф. Василенко талантливым исследователем в этой области, о чем свидетельствуют его некоторые действительно оригинальные работы […]. И я приветствую его научную деятельность в этом направлении» [29].
Стахов довольно жестко писал в конце своей статьи о пренебрежительном отношении проф. Василенко в адрес «выдающихся исследователей Пойя, Гика и других». Заниматься «ревизией» или «вообще исключать» важнейшие понятия теории золотого сечения и чисел Фибоначчи, сердито пишет директор Института ЗС, «в угоду Василенко не имеет никакого смысла. Пусть проф. Василенко остается при своем мнении, а "современная теория чисел Фибоначчи" будет развиваться вне зависимости от "мнения" Василенко. …
В заключении я предлагаю проф. Василенко заниматься конкретными исследованиями в этой области, предварительно изучив все, что сделано в этой области, и прекратить свое увлечение формальной логикой и "терминологическим крючкотворством". Извините за резковатые слова. Но я — человек простой, из глухого украинского села, высоким манерам не обучен, говорю, что думаю. За это много раз получал "шишки", но всегда, в конечном итоге, оказывался прав» [29].
Как на это отреагировал Василенко? Сначала никак; статья [27.06.2009] касалась нумерологических и теософских проблем. Следующая [30] (04.07.2009) лишь вскользь задела Стахова. В его адрес было отпущено: «В таком представлении [не будем уточнять в каком ] уравнение задает не мифические коды "золотой" пропорции [ссылка: Стахов, "Коды золотой пропорции", 1979], что алогично с точки зрения какого-либо обобщения математических констант, а серию (подкласс) дихотомических кодов…». В этой статье Василенко, между прочим, продолжает настаивать, что золотое сечение и гармония для человека и общества в целом — это очень плохо, ведет к гибели.
«Но кто сказал или доказал, что это [гармония и золотое сечение] хорошо или благотворно, чтобы от него приходить в завороженный восторг и состояние экзальтации? По всей видимости, все как раз с "вероятностью до-наоборот", когда именно данный фактор является первопричиной преждевременного старения человека, способного в идеале жить 200 и более лет. Похожие обстоятельства могут лежать и в основе гибели цивилизаций или целых народов, исчезнувших с лица земли загадочным и пока необъяснимым образом, когда в своей структуризации они вышли на уровень золотой пропорции, тем самым, разрушив собственную системность и целостность» [30].
Таких сумасбродных гипотез я не читал у Стахова; ему как-то удавалось обойти безосновательное фантазирование; более того, он иногда журил других за мистику и прочий бред.
*
* *1 Августа 2009 года свет увидела статья, в которой Василенко продолжил гнуть линию «терминологического крючкотворства». «В последние годы ряд авторов с завидной настойчивостью пестуют и превозносят некую новоявленную "математику гармонии" (МГ), претендующую на роль универсальной спасительницы для формализованного описания и моделирования бытия. При этом самих "математиков-гармонистов" нисколько не смущает тот факт, что "математики <чего-то>" не бывает.
Так, в работах [Стахова от 28.05.2009 и 22.06.2009] "математикой гармонии" предлагается назвать "современную теорию чисел Фибоначчи", как обобщение и развитие классической теории этих чисел. — Весьма странная получается сводимость широчайшего исследовательского поля, каким только можно априори на интуитивном уровне представить МГ, — к такой узкой и специфичной математической области, как числа Фибоначчи» [31].
Ну, решил человек назвать кота «Васькой», что ж тут вспоминать соседа, которого так же зовут. Василенко пишет: «в математике мы практически не отыщем такого раздела, который так или иначе не увязывался с понятием гармонии. В своем большинстве различные направления современной математики затрагивают и отражают многообразные аспекты гармонии в ее широком представлении (понимании). Кроме того, идеи гармонии уже давно вошли составляющими во многие разделы современной математики: системный анализ и теория множеств, моделирование, сложные системы, топология и геометрия, комбинаторика, алгебра и т.д.
С другой стороны, на сегодня не известно ни одного математического приложения, которое возникло бы в результате абстрагированного рассмотрения самой гармонии» [31].
В этом же ключе автор рассуждал еще на четырех страницах, хотя основа этой статьи — вполне конкретная. В ней рассказывается о геометрии «золотого» деления отрезка, а также как построить правильный семиугольник и фрактальные многоугольники. Всё очень интересно, доходчиво, школьникам и студентам полезно. Но в конце опять: «Гармония — это не процесс и не явление. Это больше философия и совокупность сторон и состояний мироздания со стрелой времени и глобальностью проявления: от микро- до макросистем, когда трудно провести даже условные линии водоразделов, выделив главные и второстепенные (лишние) направления» [31].
Сочувствую я Стахову, тяжело спорить с таким философствующим математиком. 4 Августа 2009 года его терпению наступил конец. В статье под названием «В который раз о «Математике Гармоиии» (специально для проф. С.Л. Василенко)» директор Института ЗС объявил своего ученика и единомышленника плагиатором. В подразделе, названном «Анализ научных работ С.Л. Василенко в области чисел Фибиначчи и золотой пропорции» он написал:
«Общее заключение по работам С.Л. Василенко следующее. Он весьма поверхностно знаком с современной литературой по этой проблеме и большинство его "научных результатов" — это просто повторение математических результатов, полученных другими авторами, в частности, английским математиком Вайдой, украинским архитектором Боднаром, и также моих результатов, опубликованных на сайте «Академии Тринитаризма» и в журнале «Chaos, Solitons and Fractals”. Да это и понятно — имел ли время С.Л. Василенко знакомиться с работами в области золотой пропорции, занимая должность главного гидролога да еще одновременно работая над кандидатской (1998), а затем докторской (2007) диссертациями, которые, судя по названиям, никакого отношения к золотой пропорции не имели. В научной среде такие "вольности", которые допустил Василенко в своих статьях, называется очень неприятным словом — ПЛАГИАТ (правда, в хорошо завуалированном виде)» [32].
Стахов процитировал самый обидный для него отрывок из последней работы Василенко: «Словосочетание "Математика Гармония" (МГ) вполне и главным образом допустимо для литературно-художественного образа или научно-популярного изложения общих представлений об использовании математических приемов в описании бытия и гармонии мира. Но в качестве научного термина оно не желательно, слабо обосновано и даже вредно, поскольку изначально порождает бессмысленность и отсутствие логической сопоставимости двух совершенно разных и глубоких по содержанию словесно-понятийных форм» [31].
Директору Института ЗС ничего не остается делать, как объяснить занудному критику свою правоту. На написание объемистой статьи с двумя десятками наименований русско- и англоязычных источников у него ушло три не самых счастливых в его жизни дня. В «Заключении» он презрительно бросил своему обидчику:
«Печально, когда новичок в нашем деле начинает походя судить о серьезных научных проблемах. Мне не хочется вступать в дискуссию с проф. Василенко по существу и обсуждать его пустые разглагольствования по поводу предмета, в котором он не является профессионалом. На каком-то этапе мне казалось, что проф. Василенко все же серьезный ученый, способный объективно оценивать труд и научные результаты других ученых. Оказалось, что я ошибся. И пусть его новая публикация [31] останется на его совести. Всякая критика должна быть конструктивной. А делать безответственные заявления для того, чтобы просто «попиариться» — значит, играть роль "слона в посудной лавке", главная задача которого разрушить все, что попадается на его пути, не размышляя о последствиях своих действий. Время покажет, кто из нас прав.
В течение тысячелетий не угасает интерес к Золотой Пропорции и Платоновым Телам, а также к числам Фибоначчи. Мне удалось развить и обобщить это направление и доказать его практическую полезность для современной математики, математического образования, информатики и всего теоретического естествознания. Конечно, моя теория далеко не безупречна и является только первым шагом в создании "Учения о Гармонии Систем", которое может перевернуть всю современную науку. Но этот этап в развитии "Учения о Гармонии" крайне необходим и подготовит плацдарм для создания новых, более общих теорий. Я верю в свое научное направление и считаю, что "Математика Гармонии" займет достойное место в современной науке» [32].
Я был заворожен чтением этой дискуссии, с жадностью следил за ее драматическим развитием. Кому не интересно знать, что напишет противник? Думаю, вся многотысячная армия посетителей сайта «Академии Тринитаризма» пристально наблюдала за ходом полемики.
«Довольно забавное зрелище наблюдать со стороны, как хохлы таскают друг друга за чубы, — начал иронично Василенко. — Подобный образ приходит на ум каждый раз после эмоциональных высказываний директора Института ЗС, хотя такое занятие явно не для гуру, который по логике должен быть над схваткой, а не в ее плену.
Не успела, как говорится, высохнуть типографская краска на сайте "Академии Тринитаризма" после публикации работы [31] о геометрических закономерностях гармонии, где высказаны некоторые критические замечания всего лишь по поводу лингвистической и научной некорректности словосочетания (!) "математика гармонии" (МГ), как немедленно последовала малопонятная бурная реакция [32] с подменой смыслов и беспочвенными обвинениями. Об уровне, толерантности или форме полемики и говорить не приходится, в виду слабых признаков таковой и переводом дискуссии в эпистолярный жанр» [33].
Нет, дорогой критик, похоже, вы достали старика, здесь никакой гуру не выдержит. Далее Василенко начинает выкладывать свои аргументы, в частности, такой: «Золотое сечение — хотя и уникальный, но все-таки гипотетический и абстрактный предмет, особая роль которого в мироздании, возможно, сильно преувеличена» [33]. Вот те на! То у него золотое сечение определяет форму раковин, упаковку семян в шишках и подсолнухах, то вдруг «гипотетический и абстрактный предмет». Как этот автор может писать о «сильном преувеличении» золотого сечения, когда сам расширил его влияния на все мироздание, назначил ответственным за гибель целых народов и смерь отдельно взятого человека. Нелогично. И тут же: «Про ЗС точно неизвестно, вода же действительно является матрицей (маткой) жизни». А Белянин утверждал, что талая вода имеет молекулы в форме «золотого» треугольника — или он ошибался?
После небольшой лекции о свойствах и пользе воды Василенко написал несколько фраз, которые очень больно читать 70-летнему старику. «Создается впечатление кризиса жанра, когда в отсутствие собственных свежих идей происходит малопродуктивная трата времени с бессистемной беготней по чужим статьям с выискиванием предмета нравоучительных назиданий. Хотя было бы намного полезней для науки больше уделять внимания собственным научным изысканиям» [33].
На этот низкий выпад бедный старик кинулся припоминать, что он опубликовал за последние пять лет «в ведущих международных журналах и сборниках». Перед этим он выделил особенно обидные для него слова: «Одни и те же основные результаты в своем неизменяемом многие годы ассортименте им [Стаховым] продублированы (пересказаны) десятки раз в разных публикациях так, что о них просто невозможно не спотыкаться на каждом шагу» [33].
Стахов перечислил 22 статьи и одну совсем новую книгу «The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science», которая должна вот-вот выйти в издательстве «World Scientific» [34]. Неплохо, очень даже неплохо для 70-летнего старца. Пускай в них представлены идеи, которые я не приветствую, но утверждать, будто у Стахова наблюдается «кризис жанра» (читай, «старческий маразм»), никак нельзя, а главное, некрасиво так говорить.
Мало того, что Василенко не прав по существу, он еще больше осрамился, выставив это «обвинение» пожилому человеку. Если бы директор Института ЗС за последние пять лет не написал ни строчки, никакой бы вины в этом не было. У людей бывают разные периоды творческого подъема и падения. Какие здесь могут быть претензии со стороны интеллигентного и умного человека? К сожалению, Василенко опускается до какой-то мелочности, провоцируя старика на ответные шаги, которые симметрично тоже оказываются на не высоком уровне.
Критик, а правильнее теперь сказать склочник, написал: «проф. А. Стахов находится в перманентном конфликте с авторами, которые когда-то были его друзьями, единомышленниками или (как я) учениками-заочниками» [33].
Профессор профессору ответил: «Да, действительно, характер у меня не сладкий. И некоторым "новым золотосеченцам" типа С.Л. Василенко не очень нравится моя прямая и бескомпромиссная критика их публикаций. Поэтому эти исследователи через некоторое время, к сожалению, превращаются в моих врагов. Их немного, но они есть.
Но почему С.Л. Василенко не пишет, сколько у меня появилось новых друзей и последователей за тот период, в течение которого я возглавляю Институт Золотого Сечения! Для этого достаточно просмотреть список поздравлений, присланных мне к 70-летию, на моем юбилейном сайте http://sites.google.com/site/alexeystakhov/ Мне прислали поздравления около 60 человек. С большинством из них я не знаком. И всем им я хотел бы выразить благодарность за эти поздравления. Все они — мои новые друзья и поклонники, которые понимают и осознают важность всего того, что я делаю и уже сделал в современной теории золотой пропорции. Время покажет, кто из нас прав, уважаемый господин Василенко. Я прошу Вас только об одном — давайте прекратим эту бесполезную дискуссию» [34].
Дискуссия на этом не прекратилась, но я все же не стану ее дальше комментировать. Читателю, наверное, давно всё уже ясно. Ясно, например, что нужно научиться прощать людям какие-то их слабости, особенно когда ведется действительно научный спор. В этом смысле сам я не могу похвастаться безупречной позицией, нередко перехожу на личности. Но, понаблюдав за дискуссией Стахов – Василенко, кое-что понял и впредь постараюсь быть внимательней.
И последнее, быть может, самое главное. В целом я не согласен с учением о гармонии, золотом сечении и числах Фибоначчи с точки зрения философии. Однако и Стахов, и Василенко проделали большую работу в области чистой математики. Не важно, какого мировоззрения они придерживаются, важно, что они открыли немало математических уравнений, а это принадлежит уже вечности. В отличие от релятивистов их математика носит конструктивный характер.
Возьмите, например, релятивистские формулы, описывающие эффект Доплера — ни физического, ни математического смысла в них нет, одни спекуляции. А полюбуйтесь на гиперболические функции золотого сечения, над которыми работали Стахов, Ткаченко и Боднар — это ведь песня! Ниже приводятся их графики и основные соотношения, взятые из статьи Василенко [35]. В отличие от традиционных гиперболических функций, в которых используется число e, в них подставляется золотое число φ; сравните:
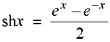

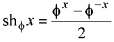





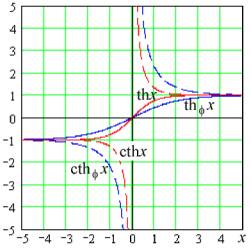












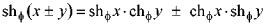








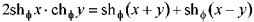


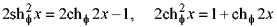







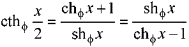
1. Белянин В.С. Владел ли Платон кодом золотой пропорции? Анализ мифа, 04.06.2006 http://www.a3d.ru/archi/stat/182.htm.
2. Василенко С.Л. "Золотой разговор" с Евклидом // «Академия Тринитаризма», М., Эл № 77-6567, публ.15649, 1575-vs.pdf, 12.11.2009.
3. Стахов А.П. Под знаком "Золотого Сечения": Исповедь сына студбатовца. Глава 3. Что такое "золотое сечение"? 3.2. Геометрическое определение "золотого сечения" // Академия Тринитаризма. — М.: Эл. № 77-6567, публ.13134, 24.03.2006.
4. Стахов А.П., Райлян И.Г. "Золотая" научная парадигма: этапы большого пути от Пифагора, Платона и Евклида до "Математики Гармонии" // Академия Тринитаризма. — М.: Эл. № 77-6567, публ.15615, 26.10.2009.
5. Стахов А.П. Еще раз о математической истории Золотого Сечения // Академия Тринитаризма. М.: Эл. № 77-6567, публ.13714, 25.08.2006.
6. Белянин В.С. К вопросу об исторической теме при изучении золотой пропорции. — 2006. — http://www.a3d.ru/architecture/stat/183.
7. Белянин В.С. Еще раз к вопросу об исторической теме при изучении золотой пропорции. — 2006. — http://www.a3d.ru/architecture/stat/184.
8. Стахов А.П. Есть у меня Белянин на примете... // Академия Тринитаризма. — М.: Эл. № 77-6567, публ.13799, 20.09.2006.
9. Herz-Fishler, Roger. A Mathematical History of the Golden Number. Dover Publications, Inc. N.Y., 1998.
10. Начала Евклида. Книги I–VI (1948) VII–X (1949) XI–XV (1950). Пер. с греч. и комментарии Д.Д. Мордухай-Болтовского при редакционном участии М.Я. Выгодского и И.Н. Веселовского. — М. –Л.: ГИТТЛ, 1948 – 1950.
11. Стахов А.П. От «Золотого Сечения» к «Металлическим Пропорциям». Генезис великого математического открытия от Евклида к новым математическим константам и новым гиперболическим моделям Природы // Академия Тринитаризма. — М.: Эл. № 77-6567, публ.14774, 16.04.2008.
12. Стахов А.П. «Деление отрезка в крайнем и среднем отношении» и «золотое сечение» — это одна и та же задача? Знали ли Пифагор, Платон и Евклид о «золотом сечении»? // «Академия Тринитаризма», М., Эл № 77-6567, публ.15651, 13.11.2009.
13. Василенко С.Л. Обобщенное уравнение гармонической пропорции. Теория и приложения // «Академия Тринитаризма», М., Эл № 77-6567, публ.15325, 1110-vs.pdf, 06.06.2009.
14. Стахов А.П. Математика Гармонии как новое междисциплинарное направление современной науки // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.12371, 19.08.2005.
15. Стахов А.П. О "золотых" алгебраических уравнениях (реплика на статью С.Л. Василенко) // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.15331, 09.06.2009.
16. Василенко С.Л. Стилистический ряд индуцированных отклонений (часть 1) // «Академия Тринитаризма», М., Эл № 77-6567, публ.15343, 1118-vs.pdf 15.06.2009.
17. Стахов А.П. В который раз о «Математике Гармонии» (специально для проф. С.Л. Василенко) // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.15450, 04.08.2009.
18. Стахов А.П. Отклик на публикации С.В. Василенко на сайте «Академия Тринитаризма» // «Академия Тринитаризма», М., Эл № 77-6567, публ.15119, 24.02.2009.
19. Василенко С.Л. Асимптотика "золотого" сечения // «Академия Тринитаризма», М., Эл № 77-6567, публ.15252, 25.04.2009.
20. Стахов А.П. Некоторые замечания по поводу статьи С.Л. Василенко «Асимптотика «золотого» сечения» // «Академия Тринитаризма», М., Эл № 77-6567, публ.15253, 26.04.2009.
21. Василенко С.Л. Основы теории рационального золотого сечения в целочисленных переменных // «Академия Тринитаризма», М., Эл № 77-6567, публ.15274, 2057-vs.pdf, 08.05.2009.
22. Неймайр М. История земли (в 2-х томах). Т. 2. — М.: Терра, 1994.
23. Крумбегель Г., Вальтер Х. Ископаемые. — М.: Мир, 1980.
24. Василенко С.Л. «Золотые» сечения в распределении Парето // «Академия Тринитаризма», М., Эл № 77-6567, публ.15292, 2066-vs.pdf, 17.05.2009.
25. Василенко С.Л. Общее и частное в систематике золотой пропорции. Часть перая // «Академия Тринитаризма», М., Эл № 77-6567, публ.15307, 2073-vs.pdf, 28.05.2009.
26. Василенко С.Л. Общее и частное в систематике золотой пропорции. Часть вторая // «Академия Тринитаризма», М., Эл № 77-6567, публ.15349, 1120-vs.pdf, 17.06.2009.
27. Василенко С.Л. "Золотые ряды" Фибоначчи с произвольными начальными условиями // «Академия Тринитаризма», М., Эл № 77-6567, публ.15295, 2067-vs.pdf, 19.05.2009.
28. Стахов А.П. По поводу «золотых» рядов Фибоначчи с произвольными начальными условиями (комментарий статьи С.Л. Василенко) // «Академия Тринитаризма», М., Эл № 77-6567, публ.15299, 20.05.2009.
29. Стахов А.П. Ответ С.Л. Василенко // «Академия Тринитаризма», М., Эл № 77-6567, публ.15350, 18.06.2009.
30. Василенко С.Л. Многомерный синтез структурной дихотомии // «Академия Тринитаризма», М., Эл № 77-6567, публ.15376, 1132-vs.pdf, 04.07.2009.
31. Василенко С.Л. Геометрические образы и закономерности гармонии // «Академия Тринитаризма», М., Эл № 77-6567, публ.15445, 1141-vs.pdf, 01.08.2009.
32. Стахов А.П. В который раз о «Математике Гармоиии» (специально для проф. С.Л. Василенко) // «Академия Тринитаризма», М., Эл № 77-6567, публ.15450, 04.08.2009.
33. Василенко С.Л. Стилистический ряд индуцированных отклонений. Часть вторая // «Академия Тринитаризма», М., Эл № 77-6567, публ.15467, 11.08.2009.
34. Стахов А.П. О моих новых научных результатах в области теории «золотого сечения и чисел Фибоначчи», опубликованных в ведущих международных журналах и сборниках за последние 5 лет.(ответ С.Л. Василенко) // «Академия Тринитаризма», М., Эл № 77-6567, публ.15470, 13.08.2009.
35. Василенко С.Л. Гиперболические функции «золотого» сечения // «Академия Тринитаризма», М., Эл № 77-6567, публ.14931, 05.12.2008.





