Конец науки

Акимов О.Е.

15. Ответы О.Е. Акимова — А.П. Стахову (III)

О красоте и науке

Стахов пишет: «Наука и искусство. Обе эти великие сферы человеческой деятельности, на первый взгляд внешне разные и далекие друг от друга, на самом деле переплетены между собой незримыми узами. И самым крепким связующим звеном между ними является красота» [1, п. 13.1.1].

Нет, не правильно, их разделяет непреодолимая пропасть. Искусство — субъективно и относительно. Наука связана с истиной, которая, хотя и носит часто относительный характер, но путем двух-трех или большего числа итераций приближается к своему абсолюту; примеров тому масса.

Сегодня всё-таки точно известно, что Земля вращается вокруг Солнца, а не наоборот. Было также достоверно установлено, что явление теплоты вызвано механическим движением микрочастиц, а не особой материей — теплородом, вызывающим якобы тепловые явления в веществе. И теория флогистона (особое горючее вещество) была отвергнута Лавуазье, когда он открыл кислород и показал, что пламя и сильный разогрев вызваны процессом окисления.

О какой красоте здесь может идти речь? Внешне теории теплорода и флогистона выглядели и проще и симпатичнее, разработанных позже теорий. Особенно сложной является кинетическая теория Больцмана, для которой пришлось разрабатывать специальный очень сложный математический аппарат статистической физики. Кроме того, возникает непреодолимая проблема критерия отбора «красивых» теорий.

Стахов предлагает воспользоваться критериями красоты, выработанным шотландским философом XVIII века Френсисом Хатчесоном, сформулированными в его «Исследованиях о происхождении наших идей красоты и добродетели в двух трактатах»:

1) красота есть единство в многообразии;
2) красота заключена во всеобщности научных истин;
3) научная красота — это обретение неочевидной истины.

И как этим добром распорядиться в конкретном научном поиске, если не удается договориться относительно красоты Джоконды? Разъяснения Волошинова на сей счет выглядят банально. В частности, по первому пункту, читаем: «... Любая математическая теорема содержит в себе бесчисленное множество истин, справедливых для каждого конкретного объекта, но в то же время все эти конкретные истины собраны в единой общей для всех истине — теореме. Например, теорема Пифагора справедлива для бесконечного множества конкретных прямоугольных треугольников, но все это многообразие треугольников обладает единым общим свойством, описываемым теоремой».

Для разъяснения второго пункта упор сделан на Ньютона: «Когда исследуют природу, подобной красотой обладает познание определенных великих принципов или всеобщих сил, из которых вытекают бесчисленные следствия. Таково тяготение в схеме сэра Исаака Ньютона ... И мы наслаждаемся этим удовольствием, даже ели у нас нет никаких перспектив на получение какой-либо иной выгоды от такого способа дедукции, кроме непосредственного удовольствия от созерцания красоты».

По третьему пункту сказано: 2 × 2 = 4 — «очевидная истина», нам нужно искать скрытую, вспоминают Гераклита («Скрытая гармония сильнее явной») и цитируется снова Волошинов: «Только открытие истин, спрятанных от нас наукой или природой, открытие, требующее усилий, доставляет нам в конце пути истинное наслаждение — познание неведомой истины» [1, п. 13.1.1].

Как такая расплывчатая эпистемология может помочь в деле исследования, например, конкретных квазикристаллов и фуллеренов?

Волошинов приводит пример, который лишний раз подчеркивает его незнание истории развития естествознания. В учебнике под редакцией Стахова дается цитата из его книги: «блестящим примером торжества простоты в науке является развитие взглядов человечества на устройство Мироздания». «Как известно, — перебивает Волошинова Стахов, — гелиоцентрическая система Николая Коперника (1473 – 1543) позволяла более просто объяснить суть движения планет относительно неподвижных звезд по сравнению с гелиоцентрической системой Клавдия Птолемея (II в.), то есть более простая научная теория пришла на смену более сложной» [1, п. 13.1.2].

Это не так. Теория Коперника была сложнее Птолемеевой, поскольку он не знал, что ось Земли сохраняет неизменное положение в пространстве, когда планета обходит по кругу центральное тело. Для удержания ее в пространстве в неизменном положении он придумал противодвижение, компенсирующее, как он ошибочно себе представлял, поворот земной оси. Так как орбитами планет у него были окружности, а реально планеты движутся по эллипсам, его система мира была менее точной, чем птолемеева. Причем за счет подбора нужных радиусов и периодов обращения эпициклов и деферентов в системе Птолемея можно было получить эфемериды с минимальной погрешностью. Гелиоцентрическая же система была косной и не поддавалась точной настройке, так что для Марса, движущегося по сильно вытянутой траектории, а также для Луны Копернику пришлось сохранить птолемеевы деференты и эпициклы.

Астрономы задавались вопросом, зачем нужен такой уродливый гибрид, когда в геоцентрической системе мира все движения планет объясняются с единых позиций и так точно рассчитываются эфемериды?

Датский астроном Тихо Браге прославился точностью измерения положения светил на небе. Оптические приборы для наблюдения за объектами ночного неба в его время еще не появились, но механические измерительные устройства начали совершенствоваться. Помимо разработанной им базисной системы отсчета он в своем Ураниборге (Дворц астрономии) установил огромный визир. Точность отсчета делений дуги с его помощью удалось достичь невиданной величины — 1/6 угловой минуты. С помощью этой установки он наблюдал звезды и планеты в течение двадцати лет. Зная более точные координаты планет, он понял, конечно, что система Коперника никуда не годится. Но в ней были определенные достоинства, которые Тихо Браге решил сохранить для своей новой системы мира. В системе мира Браге Солнце вращалось вокруг Земля, но планеты вращались вокруг Солнца. Такая необычная система мира исправляла некоторые неточности системы Коперника, но приобретала новые недостатки.

Браге заложил основы наблюдательной астрономии, которые позволили ему довольно точно определить величину прецессии земной оси (51" в год) и открыть годичное неравенство и вариацию в движении Луны. Он также составил таблицы рефракции света в земной атмосфере и учитывал влияние этого искажающего фактора на положение светил на небе. Без этих его уточнений Кеплер никогда бы не открыл свои три закона движения планет. Открытие же их произошло следующим образом.

После смерти Браге в 1601 году Кеплер приступил к внимательному изучению всего необъятного числового массива долгот и широт, накопленного в течение 20 лет непрерывных наблюдений семи планет и 788 звезд. В результате кропотливой работы, которую он начал еще при жизни Браге, им была вычерчена странная кривая движения Марса на фоне звездного неба. Сначала он не понял, что это за кривая и куда номещать Солнце. Потом догадался, что это эллипс, а Солнце надо помещать в один из его фокусов. Далее он попытался эллипс пространственно совместить с моделью своего учителя, Тихо Браге; попытка не увенчалась успехом. Наконец, он понял, что этот эллипс может устранить один из многих недостатков системы Коперника, а именно, деферент и эпицикл для Марса.

Таким образом, в результате упорного многолетнего труда в 1609 году появилась «Новая астрономия, причинно обусловленная, или Физика неба, изложенная в исследованиях о движении звезды Марс, по наблюдениям благороднейшего мужа Тихо Браге». Современники Кеплера не сразу приняли его эллиптическую систему мира как раз из-за ее непривычности, а значит, и сложности. Никто не понимал, какая сила заставляет планеты двигаться не строго по окружности, а по вытянутым траекториям, причем с различной скоростью.

Возможно, эту странную систему мира, которая была не менее радикальна, чем система мира Коперника, никто бы так и не принял, но Кеплеру удалось открыть три названных его именем закона, которые поддавались проверке. Первый закон гласит: Солнце находится в одном из центров эллипса. Второй: движение планеты по эллипсу происходит с переменной скоростью таким образом, что площади, описываемые радиус-вектором планеты в одинаковые промежутки, равны между собой.

Эти два закона Кеплер проверял в течение нескольких лет. Наконец, в 1619 году вышла его «Гармония мира», в которой наряду с мистическими пифагорейско-платоновскими фантазиями о пяти правильных многогранниках, был сформулирован третий его закон. Он гласит: квадраты времени обращения планет вокруг Солнца относятся как кубы их средних расстояний от Солнца.

Гармония мира

В последствии всю «музыку небесных сфер», которая красочно расписывалась в его «Гармонии мира» и которой восхищаются все гармонисты-золотоискатели, профессиональные астрономы выбросили из своей рациональной науки как издержки религиозного сознания ученого, оставив в сухом остатке только три его закона.

Для утверждения гелиоцентрического строения мира Кеплер сделал намного больше Галилея, после разъяснений которого книгу Коперника запретили. Он дал в руки астрономов первые количественные законы, которые можно было проверить на практике. Именно они спасли гелиоцентрическую систему мира от забвения, как это уже было в античные времена.

То, что кажется сегодня Стахову и Волошинову простым, не было таковым во времена Коперника, Галилея и Кеплера. Почему не была принята гелиоцентрическая система мира Аристарха Самосского (320 – 250 до Р.Х.), данными наблюдений которого, между прочим, пользовался Птолемей? Именно потому, что после него не нашлось античного Кеплера, который бы предложил эллипсы и три закона для них. Кеплер Нового времени тоже никогда б не состоялся, если бы ему в руки не попал архив Тихо Браге с точнейшими астрономическими данными, которых не было у античных астрономов.

В пределах точности измерений параметров орбит того времени законы Кеплера работали превосходно, но никто не понимал, какая сила заставляет планеты двигаться не строго по окружности, а по вытянутым траекториям. Выход из тупика нашел Роберт Гук. Он сформулировал всемирный закон тяготения, согласно которому сила притяжения между двумя телами прямо пропорциональна их массам и обратно пропорциональна квадрату расстояния между притягивающими телами.

К этому времени Гук принял в члены Королевского общества, которое он возглавлял, молодого геометра, Исаака Ньютона. Гук попросил его проверить на совместимость открытого им закона всемирного тяготения и трех законов Кеплера. Эта чисто математическая задача была успешно решена геометром и легла в основание капитального труда под названием «Математические основы натуральной философии».

Newton 1665	Newton 1703

Первое издание сочинения Ньютона вышло в 1686 году, в котором не было имени Гука. Автор решил открытый Гуком закон присвоить себе, так как считал, что председатель Королевского общества предложил лишь гипотезу, а он превратил ее в закон. Ньютон присвоил также результаты оптических экспериментов Гука и уничтожил после его смерти в 1703 году все его неопубликованные работы. Ньютонова «Оптика», куда вошли результаты опытов Гука, вышла в 1704 году. Ньютон издевался также над королевским астрономом Джоном Флемстидом. Он вызвался опубликовать составленный им звездный атлас, но сделал всё, чтобы он не вышел. Между тем, Флемстид был тем первым астрономом, который для наблюдения за небесными светилами использовал телескоп. В итоге, зло, которое Ньютон принес в науку, перевешивает его позитивный вклад в нее.

В третьей книге ньютоновских «Начал», которая называется «Система мира», в разделе посвященной Луне, можно прочитать: «Наш соотечественник Горрокс первый предположил, что Луна движется по эллипсу вокруг Земли, находящейся в нижнем его фокусе. Галлей поместил центр эллипса на эпицикл, центр которого равномерно обращается вокруг Земли; от движения по эпициклу и происходит вышесказанные неравенства в виде прямого и попятного движения апогея и изменений величины эксцентриситета» [2, с. 585].

Итак, физик-геометр Ньютон, астроном Эдмонд Галлей, в честь которого названа знаменитая комета, а также другие астрономы продолжали включать в свои «системы мира» птолемеевы эпициклы и деференты, с помощью которых можно было рассчитать эфемериды. Почему они это делали? Да потому что с помощью методики Птолемея легко и просто описать движение Луны. Луна – Земля – Солнце образуют систему гравитационного взаимодействия из трех тел. Задача по нахождению траекторий движения трех тел не решена до сих пор. Таким образом, после выхода в свет в 1543 году труда Николая Коперника «Об обращениях небесных сфер» идеи Птолемея продолжали фактически жить вплоть до начала 20-го века, когда, наконец, были разработаны очень сложные, с точки зрения математики, методы расчета траектории Луны на основе быстросходящихся рядов Пуанкаре.

Человека, занимающегося наблюдательной астрономией, мало интересует физика; ему нужны надежные прогнозы появления планет в заданной точке звездного неба. Например, 30 мая 2010 года, ровно в 3 часа ночи он решил посмотреть, как выглядит Марс. Он берет заранее составленные для него эфемериды и направляет объектив своего телескопа в точку А. Каким способом была рассчитана координаты точки А, его не интересует, главным для него является точность ее положения на небе.

Вот почему, Саймон Ньюком, таблицы которого в 19-м веке вытеснили все прочие, пользовался абсурдной, с точки зрения физики, формулой Холла для всемирного закона тяготения:

F = GMm / r ^{(2 + δ)},       где δ = var.

Единственным оправданием для этой подгоночной формулы был тот факт, что она давала минимальные погрешности при расчетах эфемерид. С помощью этой формулы ему удалось компенсировать и аномальную невязку, равную 42" в столетие, для перигелия Меркурия. Поправка к закону тяготения Гука составила δ = 161,2 · 10 ^–9. Аналогичными подгонками после Ньюкома занимался уже в 20-м веке Джеральд Клеменс, который также не обращал внимание ни на какие физические теории гравитации вроде общей теории относительности.

Стахов и Волошинов ошибаются не только в отношении систем мира Птолемея и Коперника, но и по всем ключевым вопросам, касающимся истории естествознания и математики. Развитие не происходит от сложного к простому, иначе цивилизация развивалась бы вспять — от космического корабля и компьютера в сторону мотыги и каменного топора. Свой тезис они проиллюстрировали на нескольких примерах вроде скандально известной формулы E = mc², которую Эйнштейн, позаимствовав ее у Пуанкаре и Дж. Дж. Томсона, так и не смог вывести математически строгим путем.

Но посмотрите, таблица химических элементов Аристотеля состояла из пяти элементов: земля, вода, воздух, огонь и эфир; в таблице Менделеева число их перевалило за сотню. Теории, пришедшие на смену двух учений о флогистоне и теплороде, созданные Лавуазье и Больцманом, тоже намного сложнее своих предшественниц. Общая теория относительности основывается на дифференциальной геометрии Римана, квантовая механика — на теории групп; обе никак не назовешь простыми. Таким образом, в основание 13-й главы нового учебника Стахов заложил неверный принцип.

О типах мышления

Стахову кажется, что «золотое» число Ф выглядит особенно красиво:

Я так не считаю, эта дурная бесконечность меня раздражает. Далее Стахов цитирует Дирака: «Красота является критерием истинности физической теории» и дает расшифровку этого тезиса: «Я чувствую, что теория, если она правильна, должна быть красивой (beautiful), так как мы руководствуемся принципом красоты, когда устанавливаем фундаментальные законы. Так, в исследованиях, опирающихся на математику, мы часто руководствуемся требованием математической красоты. … Дело обстоит так, будто Бог создал Вселенную на основе прекрасной математики и мы сочли разумным предположение, что основные идеи должны выражаться в терминах прекрасной математики» [1, п. 13.1.3].

Очевидно, Эдуард Сороко вместе с Альбертом Эйнштейном руководствовались этим принципом, когда создавали свои теории. Увы, критерии Дирака, Хатчесона и разъяснения Волошинова не помогают избежать грубых математических ошибок. Более того, эти ошибки появляются по причине именно вот таких спекулятивных критериев.

Ошибка Стахова состоит в том, что он опирается не на факты науки, а на мнения сомнительных личностей. Радзюкевич, помнится, в написанных им текстах несколько раз признавался в любви к В.П. Зубову. Я тогда подумал про себя: «Кто ж такой Зубов? Наверное, большого ума человек». И вот уже для опровержения Радзюкевича, приходится углубляться в книги Зубова, чтобы, разобравшись в его ошибках, рассказать про них Радзюкевичу. Мне кажется, человек должен стараться всё-таки жить своим умом, особенно это касается тех, кто называет себя ученым.

Никакого алгоритма научного поиска Дирак, Хатчесон и Волошинов не дают. Ладно, еще Дирак, он хоть что-то сделал для науки, а два других, чем отличились? Чему может научить человек, который сам ничего для науки не сделал? Между тем, с точки зрения современной нейропсихологии переживания человеком красоты скорее мешает познанию окружающего его мира, чем помогает. Ниже этот тезис постараемся обосновать, но сначала немного критики.

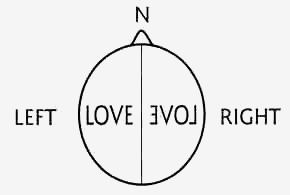
Левое и правое полушарие мозга человека по Мельхиседеку [3].

Друнвало Мельхиседек в подразделе «Структура человеческого мозга» написал: «На этом рисунке левое полушарие представляет мужской аспект, правое полушарие — женский, и связаны они с помощью мозолистого тела (corpus callosum). Согласно Тоту [египетское божество, с которым общался Мельхиседек], природа этих двух полушарий такова: левая, мужская составляющая, видит всё абсолютно логично — можно сказать: так, как оно есть. Правая, женская составляющая, намного больше занята восприятием, ощущением чего-то, чем пониманием этого явления.

Женское и мужское восприятия представляют собой зеркальное отражение друг друга — как если бы между ними стояло зеркало. Если бы в мужской составляющей было вписано слово LOVE, то он видел бы его так, как оно показано. Но женская составляющая видит зеркальное отражение, тоже так, как тут показано. Когда мужская составляющая глядит на способ восприятия женской составляющей, то "он" говорит: "В этом нет никакой логики". "Она" же смотрит на него и восклицает: "Где же чувство?"

Еще одно деление мозга по Мельхиседеку [3] на лобные и затылочные части.

Далее, ещё одной тонкой перегородкой мозг разделен на четыре доли. У мужской части мозга сзади имеется доля, которая отражает, или воспринимает зеркально переднюю долю так, как показано на этом рисунке. За женской передней долей есть ещё одно зеркальное отражение этой передней доли — в задней доле мозга. За мужской логической составляющей имеется совершенно опытная составляющая, и за женская чувственной стороной имеется совершенно логическая составляющая.

Мозг устроен так, словно четыре зеркала дают четыре возможных отражения друг в друге. Позднее мы рассмотрим геометрические фигуры и вы увидите, что передняя часть мужского аспекта мозга, логический компонент, основана на треугольнике и квадрате (в двух измерениях) или на тетраэдре и кубе (в трёх измерениях).

Передняя часть женского аспекта мозга, чувственная составляющая, основана на треугольнике и пентагоне (в двух измерениях) или на тетраэдре, икосаэдре и додекаэдре (в трёх измерениях). Есть ещё диагональные пути, связывающие левую переднюю логическую часть с задней правой логической частью, и правую переднюю чувственную с задней левой чувственной частью. Так, качество зеркальности отражает сторону на сторону, перёд – назад и диагональ на диагональ. Таково согласно Тоту, наше устройство» [3].

Мельхиседек строит простую и красивую структуру мозга, как того требует гармонический принцип простоты и красоты Стахова и Волошинова. Приняв эту структуру, в следующем подразделе «Попытка дать рождение новому сознанию на Атлантиде» Мельхиседек принялся фантазировать по поводу легендарной Атлантиды примерно в том же духе, что и в предыдущем подразделе о мозге.

«Когда настало время, Наакалы из Лемурии создали духовное соответствие человеческого мозга на поверхности своего Атлантического острова. Их целью было рождение нового сознания, основанного на том, чему они научились во времена Лемурии. Они верили, что мозг должен возникнуть прежде, чем на поверхности появится тело нового сознания Атлантиды.

Помня образ человеческого мозга, данный Тотом, можно получить представление об их действиях. Прежде всего, через середину острова была проведена глухая стена высотой около 40 футов и шириной в 20 футов; она отсекла одну часть острова от другой. Для того чтобы оказаться на другой половине острова, приходилось буквально заходить в воду. Далее, под углом 90 градусов по отношению к первой стене, была проведена меньшая стена поперёк, и так остров был разделен на четыре части.

Затем, половина из этой тысячи людей, составлявшей мистическую Школу Наакал, перешла на одну сторону, а половина оставалась на другой — в соответствии с их природой. Это может означать, что все женщины оставались на одной стороне, и все мужчины отправились на другую сторону, но я понимаю это так, что данное распределение не имело отношения к физическому телу человека, но — к его или её зависимости от одной или другой стороны своего мозга. Таким образом, приблизительно половина людей составила мужскую часть мозга, а другая половина стала женской составляющей. …

Дерево Жизни на Атлантиде по Мельхиседеку [3].

Следующим шагом было проецирование на поверхности Атлантиды формы Древа Жизни. Здесь они использовали форму, составленную из 12 кругов вместо 10-ти, но 11-тый и 12-тый круги находились за пределами основной части суши; одна из точек расположилась на острове Удал и другая, на юге, оказалась в воде. Так, на основной части суши располагались десять составляющих, представивших собой конфигурацию, нам уже знакомую.

Город Посейдон на острове Атлантида по Мельхиседеку [3] и Платону.

Несмотря на то, что она распространялась на сотни миль по поверхности этой земли, они, согласно Тоту, спроецировали её с точностью до размера одного атома. Есть указание на то, что сферы Древа Жизни были использованы даже для того, чтобы наметить размеры и форму городов Атлантиды. Платон в своей книге "Критий" говорит, что главный город Атлантиды был составлен из трёх кругов суши, отделённых друг от друга водой, так, как показано на этом рисунке. Он говорит также, что город был выстроен из красного, чёрного и белого камня. Это последнее утверждение обретёт смысл, как только мы заговорим о Великой Пирамиде» [3].

Образ мыслей Мельхиседека сам по себе чрезвычайно интересен и заслуживает специального изучения. Его популярность в мире во многом объясняется этой манерой создавать глобальные теории. Теперь мы сравним его теорию мозга с тем, что известно рациональной науке о нем.

*
*   *

Мозг живых организмов прошел длительную эволюцию, которая отложилась в строении мозга. Он развивался приблизительно в том же порядке, в котором проставлены цифры на рисунке ниже. Спинной мозг появился самым первым. Он ответственен за самые примитивные реакции рефлекторного характера, которые наделены все живые существа. Прежде всего, это защитные реакции; например, человек отдергивает руку, когда случайно касается разогретого утюга.

Эволюция мозга шла от 1 до 6

Потом стал развиваться продолговатый мозг (1), в котором расположились центры, ответственные за дыхание, питание, кровообращение. Вместе с ними развивался мозжечок (2) — главный двигательный центр, отвечающий за координацию и равновесие при движении. Он хорошо развит у птиц, особенно, если его сравнивать с их передним мозгом. Лобные доли (6) — развились позже всего; это та часть мозга, которая делает человека человеком. Появление и развитие затылочного (3), среднего (4) и теменного (5) мозга происходило примерно одновременно, хотя и с характерными отличиями для отдельных видов животных (об этом популярно рассказывается в книге С.В. Савельева «Происхождение мозга» [4]).

Элхонон Голдберг, директор Института нейропсихологии и познавательных процессов Нью-йоркского университета, автор книги «Управляющий мозг: Лобные доли, лидерство и цивилизация», на богатом экспериментально-теоретическом материале доказывает, что сложнейшие мыслительные функции, ответственные за принятия обдуманных решений, осуществляются лобными долями. Не важно, кем является человек — ученым, политиком, бизнесменом, — эффективность его работы связана с передним отделом мозга, который по своим размерам самый большой, хотя и возник позже всех.

Он отделен от теменной части мозга двигательной зоной, которая радикально отличается от мозжечка (она находится в районе шва, соединяющего 5 и 6 зоны). Сигналы, идущие от мозжечка и к нему, не осознаются человеком; удержание равновесия при ходьбе, например, происходит автоматически. Второй же двигательный центр контролируется лобными долями и служит им обратной связью: человек принял решение, дальше он начинает действовать. При этом реализация решения может осуществляться в течение одного дня, месяца, года или больше. В течение этого времени «главный командный пункт» координирует целенаправленные движения человека; мозжечок такого рода действия не выполняет.

Бездействие лобных долей, в том числе по причине их повреждения, приводит к лени, апатии и безразличию. В этом случае человек прекрасно видит, слышит, что-то переживает (радость или горе), его мозжечок «на автопилоте» работает исправно, однако у него утрачено главное — внимание, инициатива, жизненная цель. Голдберг пишет: «лобные доли парализуются при слабоумии, шизофрении, травматических повреждениях головы, синдроме дефицита внимания и в целом ряде других расстройств. Раньше и чаще всего управляющие функции ослабевают, когда наступает слабоумие» [5, с. 26].

Все познавательные процессы происходят в этой части мозга. Она ответственна именно за рациональное мышление, иррациональные переживания, в том числе эстетические и религиозные расположены дальше от лобных долей.

Раньше считалось, что существует заметная разница между функциями левого и правого полушария, как об этом говорил и Мельхиседек. Левое полушарие оперирует преимущественно субъективными и качественными категориями; оно имеет дело с речью, логикой и счетом в уме. Языковое мышление называют еще вербальным; в противоположность образному мышлению, его можно назвать дифференциальным или микрооперационным.

Правополушарное мышление, ответственное за пространственную организацию, называется интуитивным; его интегральный, макрооперационный ход трудно проследить самому, тем более передать или рассказать о нем другим. Образное мышление обрабатывает в основном объективные данные, поступающие из внешнего мира конструктивными методами, т.е. через представления.

И вот оказалось, что левое и правое полушария работают вполне слаженно и однотипно, а указанное деление проходит не поперек мозга (левая – правая части мозга), а вдоль него. Конструктивное мышление осуществляется передней частью мозга, а иррационально-формальное — задней. Чем дальше от лобных долей возникает возбуждение, тем древнее образ мысли.

Теменной частью мозга человек испытывает боль, чувствует, переживает, говорит, слышит, понимает речь, осязает; затылочной — видит и распознает образы, но вся эта богатая и разнообразная деятельность происходит автоматически, как у мозжечка и продолговатого мозга, без включения лобных долей. Человек отдается праздным мечтаниям, его мысли текут как образы в сновидениях. Такого рода процесс Юнг называл расслабленным, в отличие от напряженного.

Человек, мышление которого определяется средней частью мозга, выполняет монотонную работу, напоминающую сборку картинки из пазлов. Он не задает вопросов типа: «что я делаю?» и «зачем это мне нужно?», у него плохо работает обратная связь, он редко корректирует свои планы. Однажды начав выполнять какую-либо монотонную работу, он двигается почти по инерции или по пути наименьшего сопротивления.

Каждый из нас встречал на своем жизненном пути словоохотливых женщин и мужчин, болтающих без умолка на самые разные темы, но вместе с тем очень не глубоких в своих суждениях. Оказывается, память тоже находится ближе к средней части головного мозга, чем к передней. Эрудиты соображают заметно хуже, чем люди знающие относительно немного. Их ассоциативное мышление близкого действия. Ассоциации конструктивно думающих людей — дальнего действия, они способны проводить параллели между сильно удаленными друг от друга объектами.

То, что именуется изощренностью ума или остроумием, компенсирует у них недостаток информации. Способные же люди реже включают свои лобные доли, чем неспособные. Они ленивы, в результате плохо приспособлены к окружающей среде и не добиваются успехов. Люди, лишенные больших талантов, оказываются нередко более дальновидными, энергичными, точно рассчитывающими и последовательно реализующими поставленные цели. В итоге, они делают головокружительную карьеру и добиваются всеобщего признания.

О механизме работы передней части головного мозга Голдберг пишет следующее: «Центральная роль лобных долей заключается именно в том, что организм освобождается от стереотипных репертуаров, он свободен в своем творчестве, ему открываются альтернативы. … Лобные доли — это главный управляющий мозга, способный обозревать сверху все другие функции мозга и координировать их». Передняя часть мозга, подобно дирижеру, «ведет человека к новизне, изобретениям, открытиям и приключениям. Без колоссального развития лобных долей человеческого мозга, сопряженного с развитием языковых зон, цивилизация никогда бы не могла возникнуть» [5, с. 8].

Голдберг разъясняет механизм управления: «Как только в передней части завершен отбор информации, требующейся для решения той или иной задачи, лобные доли должны "знать", хотя бы приблизительно, где эта информация хранится. Это наводит на мысль, что вся кора головного мозга каким-то образом представлена в лобных долях. … Такие репрезентации являются, естественно, не полными; они позволяют лобным долям только узнать адрес места хранения нужной информации, но не ее специфические особенности. Затем лобные доли контактируют с соответствующими частями мозга и обеспечивают поступление энграмм (единиц памяти), путем возбуждения тех нейронных сетей, которые содержат энграмму.

Таким образом, аналогия между лобными долями и главным управляющим снова оказывается здесь полезной. Подписав новый контракт, управляющий компании может не иметь технических навыков, необходимых для осуществления проекта, но он знает, кто из его персонала ими обладает; он способен правильно отобрать сотрудников для реализации проекта, опираясь на их специфические знания и умения» [5, с. 110].

Далее нет смысла углубляться в детали работы головного мозга; общую картину мы себе уже представляем. Вывод из нее будет такой: вопреки утверждениям Стахова наука должна быть отделена от искусства, религии и прочих вещей, будоражащих воображение. Чтобы эффективно решать задачи, нужно активнее задействовать передний головной мозг и, по возможности, отключать теменную и затылочную части, в которых бушуют страсти. Нельзя допускать, чтобы древние отделы мозга командовали новыми.

Если даже от рождения человек предрасположен к мало осознанным поступкам, вызванными «дикими» эмоциональными всплесками, идущими от затылочных и теменных областей, всегда существует шанс поправить природу. После рождения число нейронов при росте человеческого организма уже не увеличивается; происходит только рост аксонов, их ветвление и увеличение связей между нейронами. Но связи эти не постоянны, они меняются в зависимости от жизненных обстоятельств. Мы можем научиться контролировать чувства, вызванные сильными переживаниями, мешающими спокойно и сосредоточенно думать.

Наука — это спокойный каждодневный труд, в котором нет места для эмоциональных переживаний, ажиотажа и сенсации. Люди, создающие их, не должны работать в научной сфере в качестве исследователей. Истину в свое сознание нужно впускать осторожно, постоянно озираясь по сторонам и задавая себе неизменный вопросы: всё ли я учел, а вдруг это ошибка?

Все войны в науке и политике происходят между конструктивистами-рационалистами и формалистами-иррационалистами. Первых условно можно назвать «лобастиками», поскольку они преимущественно думают лобными долями, вторых — «затылочниками», так как эта древняя часть мозга сильно влияет на их образ мысли. Войны происходят из-за того, что затылочники из-за узости своего мышления совершенно не в состоянии понять лобастиков, лобастики, однако, прекрасно понимают поведение затылочников, но не хотят или не могут опускаться на их уровень.

В науке ситуация безнадежная, мира между двумя этими категориями людей никогда не бывает. В политике дела обстоят получше: есть на земле государства, которыми управляют лобастики. К сожалению, в странах бывшего Советского Союза политические институты не работают на лобастиков. Так получается, что электорат на все сто процентов состоит из затылочников, лобастики в избирательных списках отсутствуют (т.е. они — «неучтенка») и голосовать они не ходят. Все телевизионные компании по промывке мозгов работают на затылочников, лобастики эти передачи не смотрят.

Зато лобастики эксплуатируют затылочников в сфере бизнеса. Вся реклама рассчитана на последнюю категорию; она работает по следующей физиологической схеме. Предположим, домохозяйка оказалась в магазине, в котором продается товар, который раньше рекламировался по телевизору. У нее в спинном мозгу, отвечающим только бессознательными рефлексами, условно говоря, вспыхивает красная лампочка, во рту начинается активное слюноотделение и она, как собачка Павлова, жадно хватает стиральный порошок или что там еще рекламируют сладким голосом.

Моя жена постоянно покупала два пузырька — шампунь и ополаскиватель к нему одной какой-то фирмы, к чему я давно привык. Неожиданно она купила моющее средство другой фирмы, на упаковке которого была надпись «шампунь и бальзам-ополаскиватель против перхоти 2 в 1».

Я вспылил и стал укорять ее в том, что она не думает своей головой: «Не может шампунь и жидкость для избавления от него находиться в одном флаконе. Ты приобрела товар у каких-то дельцов-мошенников», — сказал я ей тогда. Мне стало даже интересно узнать, какой гадости они туда налили.

Однако, испытав действие жидкости «два в одном» на собственной голове, я убедился, что новый шампунь по качеству намного превосходит прежний. И тут я понял, что производители этого товара, придумывая к нему рекламу, не брали в расчет меня, а только мою жену с ее патологической ориентацией на экономию.

Возможно, представленная концепция работы головного мозга, выработанная в Нью-йоркском институте нейропсихологии и познавательных процессов и подытоженная в книге Голдберга, в чем-то не совсем точна. Но лучше уж иметь приблизительную естественнонаучную теорию, чем руководствоваться неопределенными философскими рассуждениями о красоте.

Стахов заглядывая в будущее, призывает молодежь пользоваться давно устаревшими методами. Он пишет: «Идея Гармонии Мироздания и Золотого Сечения, восходящая к Пифагорейскому учению о числовой гармонии мироздания, является древнейшей научной парадигмой, которая возникла в тот же период, как и сама наука. Эта идея относится к разряду "вечных" проблем, интерес к которой никогда не угасал в науке, но особенно возрастал в периоды наивысшего расцвета человеческой культуры. Есть все основания полагать, что последняя четверть 20-го века и начало 21-го века стали периодами своеобразного Ренессанса этой древнейшей научной парадигмы в современной науке. Современная наука, в которой преобладают процессы дифференциации, нуждается в некоторой междисциплинарной, интегрирующей и синтезирующей научной дисциплине, которая объединила бы все направления науки, искусства и технологии. И таким междисциплинарным научным направлением может стать Учение о гармонии» [6].

Дорогие девочки и мальчики, когда гармонист-золотоискатель призывает вас заняться «наукой», исчезнувшей много веков назад, бегите от него без оглядки. Вы упустите драгоценное для себя время, а в итоге ничего не получите. Науками 21-го века никогда не будут пустые манипуляции с ЗС, Платоновскими телами и охи-вздохи вокруг непонятной красоты; ими будут: информатика, микроэлектроника, компьютерные технологии, биотехнологии, генная инженерия и т.д. Спешите найти себя в этих отраслях знаний.

В самом конце 20-го века (1998 г.) произошло открытие эмбриональной стволовой клетки. Она создала предпосылки для регенерации любой специализированной ткани. Это позволит «выращивать» сердце, почки, легкие и другие внутренние органы, отказавшие работать по тем или иным причинам. Нас ждет революция не только в сфере коммуникации, начавшаяся в 20-м веке, но и в области медицины, что намного важнее для человеческого благополучия, чем Интернет и мобильник.

В связи с этим, ребята, выбросите из головы всё это пифагорейско-платоновское старье, наберите в поисковике словосочетание «стволовая клетка» и начните читать любую попавшуюся вам статью на эту тему. Заставьте работать лобные доли своего мозга и успокойте теменную и затылочную части.

О гипотезе Прокла

Стахов написал: «Единственное, с чем я категорически не согласен с Акимовым, — это с его отрицанием "гипотезы Прокла". … Я в своих работах развил "гипотезу Прокла" и показал, что введение "золотого сечения" в книге 2, книге 6 и последующих книгах "Начал", включая книгу 13, не является случайным. Золотое сечение было введено Евклидом с единственной ясной и четкой целью — построить геометрическую теорию додекаэдра — главной фигуры Мироздания. … Однако Акимов считает "гипотезу Прокла" ошибочной, ссылаясь на мнение современного историка математики Шичалина [идет цитата] … при этом Акимов должен знать, что кроме мнения Шичалина, существуют и другие точки зрения, о которых он, видимо, не знает … [идет цитата]» [7].

Я привел наиболее интересные на мой взгляд фрагменты из биографии Прокла, фрагменты из его Комментария на первую книгу «Начал» Евклида и комментарии к «Комментариям», написанные переводчиком сочинений Прокла Ю.А. Шичалиным. Говоря об ошибочности гипотезы Прокла, я опирался больше на свои собственные знания «Начал», чем на авторитет филолога Шичалина.

В разделе Белянин и Стахов: спор вокруг Евклида мною было кратко представлено содержание всех книг Евклида. Оно настолько разнообразно, что сделанное Проклом заявление выглядит слишком большим преувеличением. Он написал, что Евклид «принадлежит к платоникам и близок их философии, почему и поставил целью всего своего изложения Начал описание так называемых пяти платоновских тел». Выделенные курсивом слова Прокл плохо обдумал.

Чуть выше он заявил: «Евклид, составивший "Начала", собравший многое из открытого Евдоксом, улучшивший многое из открытого Теэтетом, а помимо этого сделавший неопровержимыми доказательствами то, что до него доказывалось менее строго». Если говорить, что целью написания «Начал» является платоновские тела, то нужно признавать, что целью Евдокса, Теэтета и тех, чьи доказательства он усовершенствовал, думали только о платоновских телах, а это ведь не так.

Евдокс написал, в частности, пятую книгу «Начал». Она посвящена теории чисел, значит, уже не всё содержание «Начал» посвящено платоновским телам. Во второй книге обсуждаются правила, которыми пользовались еще вавилоняне [8, с. 131 — 132]; в современных обозначениях они выглядят так:

1) если a = a₁ + a₂ + ... + a_n, то ab = a₁b + a₂b + ... + a_nb;
2) если a = b + c, то a² = ab + ac;
3) если a = b + c, то ad = bd + cd;
4) (a + b)² = a² + b² + 2ab;
5) (a – b)b + (b – a/2)² = a²/4;
6) (a + b)² = a² + b² + (2a + b)b;
7) если c = a + b, то a² = b² + c² – 2bc;
8) (a + 2b)² = a² + 4(a + b)b;
9) [(a + b)²/2 + (a – b)²/2] = (a² + b²)/2;
10) (a + b)² + b² = 2(a/2) 2 + 2(a/2 + b)².

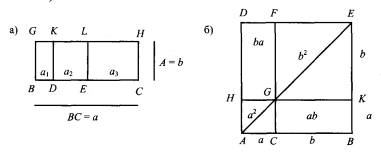
Чертежи к предложениям 1 и 4 "Начал" Евклида

Первое предложение формулируется при помощи площадей прямоугольников (рис. а): прямоугольник BH = ab равен сумме прямоугольников BK = a₁b, DL = a₂b, EH = a₃b. Следующий рис. б отвечает предложению 4 и т.д. Возьмите первую книгу «Начал», в ней доказывается теорема Пифагора (предложение 47), которая тоже не имеет никакого отношения платоновским телам. Хорошо, если процентов 5 – 10 (не хочется подсчитывать) от всего объема «Начал», как-то можно связать с платоновскими телами. Впрочем, здесь можно долго спорить, заносить, например, теорему Пифагора в актив Стахова или нет.

Между тем, способ доказательства указанных предложений и, особенно, предложения 47 из книги I, свидетельствует, что Евклид не был платоником, как ошибочно считал Прокл. Его мышление противоположно мышлению Платона. Для Евклида, как и Аристотеля — ярого противника Платона, характерен софистический или схоластический способ мышления, в которых логика превалирует над зрительным образом. В свете выше изложенного о двух типах мышления, Евклида надо отнести к ярко выраженным формалистам, Платона же — к поверхностным, с точки зрения профессиональной метематики, конструктивистам, который оперирует исключительно образами. Евклид пользуется близкими ассоциациями, которые, собственно, и создают логическую последовательность. Они не выходят из узкой теменной области мозга, в которой сосредоточены языковые центры. Евклид, как и Аристотель, абсолютно не религиозен, он дышит ровно, когда говорит о ЗС, икосаэдре и додекаэдре.

У Платона дальние ассоциации, причем они настолько далекие, что его лобное мышление захватывает затылочные области, ответственные за религиозные переживания. Платон превозносил геометрию, но геометром не был; как и Аристотель, в математике он был полным дилетантом, в отличие, скажем, от Евдокса, который, опять же, как и Аристотель, отвернулся от религии Платона и образовал свою реалистическую школу, занявшую среднее положение между Академией Платона и Ликеем Аристотеля. Евклид, как профессиональный математик, включил наработки Евдокса, но он ни за что не согласился бы включить туда какие-то Платоновские религиозные видения; это просто противоречило бы его менталитету. Когда Стахов вслед за Проклом причисляет Евклида к платоникам, он делает огромную ошибку.

Стахов написал: «Именно "гипотеза Прокла" привела меня к новому взгляду на историю математики…» [7].

В связи с этой фразой еще раз повторю: Прокл писал сочинения в основном на теологические темы. Откровенно нужно сказать, он ничего не смыслил в математике, очень непрофессионально прокомментировал первую книгу «Начал» и сделал необдуманное заявление, которому нет никакого подтверждения. Если здесь на кого-то и ориентироваться, то, прежде всего, на самого Евклида. Существуют многочисленные глубокие исследования по теме, какое влияние он оказал на развитие математики.

Некоторые вопросы истории античной математики, особенно те, что связаны с «Началами» Евклида, были рассмотрены более или менее подробно в ранее написанных подразделах: От Пифагора до Платона через Евдокса; а также начало подраздела Белянин и Стахов: спор вокруг Евклида. В последней ссылке дается обзор содержания всех книг евклидовых «Начал». Из него вытекает: золотому сечению и Платоновым телам Евклид уделял какое-то внимание, но его никак нельзя назвать доминирующим; во всяком случае, с мнением Прокла ни в коем случае соглашаться нельзя. Последующее развитие математики (о нём ниже) лишний раз это подтверждает.

«Новый взгляд на историю математики, — продолжает Стахов, — состоит в следующем. Математика формировалась под влиянием трех "ключевых проблем", которые возникли в ней на самых ранних этапах ее развития: счет, измерение и гармония. В рамках каждой из этих проблем в математике было сделано три выдающихся математических открытия:

1. Позиционный принцип представления чисел (Вавилон), который лежит в основе десятичной и двоичной систем счисления. О роли этих систем счисления в истории образования и материальной культуры (компьютерная техника) не стоит распространяться.

2. Несоизмеримые отрезки. Это открытие привело к введению иррациональных чисел – второго (после натуральных чисел) фундаментального понятия математики.

3. Золотое сечение. Иоганн Кеплер назвал ЗС одним из сокровищ геометрии и сравнил его с «Теоремой Пифагора», хотя многие современные математики не могут с этим согласиться (это их дело, но не следует забывать, что Кеплер, в отличие от тех математиков, которые его критикуют, был не только гениальным астрономом, но и гениальным математиком)» [7].

Нет, нельзя ставить рядом с двумя первыми пунктами третий; да и второй с первым не совсем корректно сравнивать. Да, греки открыли иррациональные числа, но они не знали более важных для математики вещей, в частности, нуля и отрицательных чисел, которые открыли индийцы. Иррациональные числа (корни квадратные и кубические из двух, трех, пяти и т.д.) можно заменять приближенными числами, что сейчас и делается. Но без нуля и отрицательных чисел арабы не заложили бы основы алгебры. В связи с решениями уравнений второго и высшего порядка сразу же возникает потребность в мнимых и комплексных числах. Между тем, позиционный принцип имеет продолжение в матричных агрегатах. Трудно представить себе развитие науки, в том числе физики, без матричного и тензорного исчисления.

Несоизмеримость получила некий философский резонанс, однако, с точки зрения сухой математики, иррациональные числа всего лишь один, не самый важный класс чисел. То же самое можно сказать относительно ЗС. Действительно, числа Ф и φ взаимно обратные, т.е. Ф = 1/φ или Ф × φ = 1. Другой такой пары, естественно, существовать не может, поэтому они встречаются в симметричных объектах типа икосаэдра, додекаэдра, в соотношениях между отрезками, когда в круге вписывается равносторонний треугольник, квадрат и звезда. В этом больше закономерностей, чем странностей, но гармонисты, в силу специфики своей психики, вливают в эту ложку прозы бочку поэтической лирики, т.е. некий эмоционально-эстетический смысл, часто переходящий у них в сильное религиозно-мистическое переживание.

Чтобы закрыть данную тему окончательно, давайте посмотрим на ход развития математики в целом, как это попытается сделать Стахов. Это нужно нам еще и потому, что ее развитие, особенно для Европы, не в последнюю очередь было связано с именем Леонардо Пизанского, т.е. Фибоначчи. Вокруг него у мистиков-золотоискателей сложилось немало нелепых представлений. Об этом читайте в следующем подразделе.

О том, как Мельхиседек представляет себе Фибоначчи

Сразу же оговоримся, о золотом сечении и Платоновых телах культурная общественность Европы заговорила только в эпоху Возрождения, особенно, в связи выходом тракта Луки Пачоли «О божественной пропорции». Об этом историческом эпизоде говорилось уже немало (см. Неправедная жизнь Луки Пачоли и предшествующие ему подразделы). Сейчас мы расскажем, чем интересовались математики до выхода указанного трактата. Центральной фигурой для нас будет итальянский математик Фибоначчи (он же — Леонардо из Пизы). Этому изложению предпошлем небольшой фрагмент из книги Мельхиседека, тоже касающийся Фибоначчи. Стилистика изложения нижеследующего отрывка, мне кажется, близка к стилистике Стахова, когда он толкует ход развития математики в свете ошибочной идеи Прокла. Итак, читаем рассказ о Фибоначчи в изложении Мельхиседека.

«Фибоначчи жил лет на 250 раньше да Винчи. Согласно тому, что я о нём читал, — пишет Мельхиседек, — он был монахом и часто пребывал в состоянии медитации. Он любил прогуливаться по лесам и медитировать во время прогулок. Но его левое полушарие мозга явно было в это время активно, потому что он начал замечать, как растения и цветы содержат в себе числовые соответствия.

Схемы, по которыми сформированы лепестки, листья и семена цветов, соответствуют определённым числам, и в этом списке должны значиться цветы, которые, если я правильно уловил, я думаю, он видел на своих прогулках. Он заметил, что лилии и ирисы имеют по три лепестка, а лютики, живокость и водосбор (цветок в верхнем правом углу на рисунке) — по пять. Некоторые шпорники имеют по 8 лепестков, ноготки имеют 13, некоторые астры же — 21 лепесток. Маргаритки почти всегда имеют 34, 55 либо 89 лепестков. Эти же самые числа начали встречаться ему всюду в природе, опять и опять.

Это маленькое растение на самом деле не существует; мы создали его с помощью компьютерной графики, тасуя данные, как колоду карт. Подлинное растение, на котором основана эта иллюстрация, называется трава-чихун (тысячелистник птармика); мы просто составили на компьютере графическое изображение этого растения.

Фибоначчи заметил, что когда росток травы-чихун только появляется из земли, на нём вырастает только один лист, всего один маленький листик. Затем он немного вытягивается, и на стебле вырастает ещё один листок, потом немного дальше у него вырастает два листа, потом три, затем пять и затем — восемь; после этого он выбрасывает тринадцать соцветий. Вероятно, он подумал: "Эй, это те же самые числа, которые я вижу всюду в лепестках у других цветов — 3, 5, 8, 13".

В конце концов, эта последовательность из чисел 1, 1, 2, 5, 8, 13, 21, 34, 55, 89 и так далее стала известна как последовательность Фибоначчи. Если вам известны любые три последующих числа из этой последовательности, то вы можете распознать всю закономерность: остаётся лишь сложить два последовательных числа, чтобы получить число, следующее за ними. Видите, как это работает? Это совершенно особенная последовательность. В жизни она является решающей. Пожалуй, это будет моей интерпретацией пояснения причины, по которой она является ключевой, но я изо всех сил постараюсь вам показать» [3].

Эта история показалась мне столь забавной, что вызвала острое желание в ответ на нее написать правдивую историю о жизни и деятельности Леонардо Пизанского, которого как раз и звали Фибоначчи. Мельхиседек представил дело так, будто интересующий нас числовой ряд Фибоначчи открыл, изучая морфологию растений. Ошибка, допущенная автором книги [3], довольно распространенная: многие гармонисты-золотоискатели связывают его задачу о кроликах с филлотаксисом. Кем же был на самом деле Фибоначчи, откуда взялся числовой ряд, названный в его честь, и какую научную, по-настоящему важную миссию он исполнил.

О том, как в действительности жил Фибоначчи

Леонардо Пизанский или Фибоначчи (ок. 1170 – ок. 1240) родился, жил и умер в Пизе — крупном торговом городе Италии, прославившемся «падающей» Пизанской башней, которую построили как раз при жизни Фибоначчи. Тогда многие состоятельные семьи, включая семью Боначчи, проживали в таких башнях, т.е. в укрепленных высотных зданиях, позволяющих отразить врагов и переждать осаду. Спросите, кто такой Боначчи? Отец Фибоначчи. Слово Fibonacci расшифровывается как filius Bonacci, т.е. сын Боначчи; само слово «bonacci» означает «добродушный».

 

Два вида на Пизанскую башню

После падения Римской империи в 476 году Европа более шести веков находилась в состоянии варварского оцепенения. Империя, основанная Карлом Великим на рубеже VIII и IX веков, была не долговечной. Единственным долговечным образованием явилась Священная Римская империя, основанная германским королем Оттоном I в 962 году. В нее вошли Германия Голландия, Австрия, Чехия, Франция, Италия и множество мелких государственных образований. Эту разноплеменную империю раздирали культурно-исторические противоречия, закончившиеся в 1054 году расколом христианской церкви на православную и католическую.

Постепенно, с наступлением XII столетия, начала оживать торговля. Итальянские купцы преодолевали тысячи километров, чтобы доставить и приобрести товары со всего света, даже из Индии и Китая. Самое известное дальнее путешествие на Восток совершил Марко Поло (1271 – 1295). Леонардо плавал по Средиземному морю со своим отцом Боначчи в Алжир и Египет, где находилось множество индийских и арабских деловых людей. От них он перенял очень удобную позиционную систему счета, которая сейчас называется «арабской», а до этого в Италии пользовались только «римскими» цифрами, оставшимися в наследство от культуры Римской империи.

Леонардо Пизанский, Фибоначчи (ок. 1170 – ок. 1240)

Фибоначчи повезло: он жил в благоприятное для развития интеллектуальных способностей время. Шумные рыцарские турниры, проводимые Фридрихом Барбаросса (1125 – 1190) и Ричардом Львиное Сердце (1157 – 1199), всем наскучили. В 1220 году король Сицилии и Германии Фридрих II (1194 – 1250) становится императором Священной Римской империи. Сицилией (или Неаполитанским королевством) он начал править с трех лет от роду и очень полюбил эту страну, хотя его дед, император Фридрих Барбаросса, ее терпеть не мог.

Уже в зрелые годы он провел в ней реорганизацию управления (Мельфийская конституция 1231 года). Сицилия, которая вместе с Испанией долгое время находилась под владычеством арабских властителей, превратилась в самое передовое и просвещенное государство Европы. Культура стран ислама в то время намного превосходила культуру христианского мира. Поэтому именно с Сицилии началось итальянское Возрождение.

Голова статуи Фибоначчи, город Пиза

Фридрих II получил прозвище Stupor Mundi (Чудо Мира) за свою культуру, образованность и проницательный ум, несмотря на то, что многих обижало его экстравагантное поведение. Кровавые рыцарские турниры своего деда он заменил интеллектуальными турнирами, на которых молодые люди соревновались, в том числе, и в решении математических задач. Вот на таких математических олимпиадах и проявились незаурядные способности Фибоначчи.

Юношу заметил Фридрих II и впоследствии покровительствовал во всех его благих начинаниях. Отец Боначчи дал молодому дарованию прекрасное образование. Он обучил его счету, письму, многим иностранным языкам и часто брал в торговые и дипломатические поездки в страны Средиземноморья. Сын с рвением изучал рациональные науки иноземных мудрецов, проявив особую любовь к математике.

Памятник Фибоначчи, установленный
у него на родине в городе Пизе.

Для духовного образования и воспитания молодых людей в средневековой Европе существовали учебники по «свободным искусствам», которые со времен Римской империи делились на тривиум и квадривиум. Тривиум охватывал грамматику, риторику и диалектику (умение вести спор); квадривиум включал арифметику, геометрию, астрономию, музыковедение (учение о гармонических интервалах). В Средние века Европа пользовалась учебниками математики, написанными римскими учеными Марцианом Капеллой (ок. 450) и Флавием Кассиодором (ок. 480 – 575). Здесь же нужно упомянуть епископа Севильи Исидора (ок. 570 – 636), написавшего энциклопедический словарь «Происхождения» (Origines), где разъяснялся смысл и происхождение многих научных терминов.

На протяжении всего Средневековья наиболее популярным учебником по квадривиуму был учебник, написанный Боэцием (ок. 480 – 524). Ему также принадлежат переводы с греческого на латинский язык геометрической части «Начал» Евклида (без доказательств) и «Арифметики» Никомаха. Популярность Боэция во многом объяснялась тем, что ему приписывались математические трактаты неизвестных средневековых авторов, которые он не писал. Свою громкую известность он приобрел благодаря сочинению «Утешение в философии», написанному в тюрьме, незадолго до казни. Он служил при дворе остготского короля Теодориха Великого, но был обвинен в государственной измене, брошен в тюрьму и казнен.

Римский философ, теолог и поэт Северин Боэций (ок. 480 – 524)

Благодаря помощи Фридриха II Фибоначчи издал «Книгу абака» (Liber abaci, 1202), «Практическую геометрию» (Practica geometriae, 1220), где излагалась евклидова геометрия и приводились формулы площадей и объемов геометрических фигур, а также «Книгу квадратов» (Liber quadratorum, 1225), в которой давались решения квадратных уравнений. По этим книгам учился Декарт и Эйлер. Они включали множество задач, которые до этого предлагались участникам турниров либо самим Леонардо Фибоначчи, либо его главным соперником Иоганном Палермским, придворным философом Фридриха II. В предисловии к «Книге абака» Фибоначчи писал:

«Отец мой, родом из Пизы, служил синдиком на таможне в Бужи, в Африке, куда он меня взял с собою для изучения искусства считать. Удивительное искусство считать при помощи только девяти индусских знаков мне так понравилось, что я непременно захотел познакомиться с тем, что известно об этом искусстве в Египте, Греции, Сирии, Сицилии и Провансе. Объехав все эти страны, я убедился, что индусская система счисления есть самая совершенная... Изучив основательно эту систему и все к ней относящееся, прибавив свои собственные исследования и почерпнутое из "Начал" Евклида, я решился написать это сочинение».

Вот та главная миссия, которую исполнил Фибоначчи: он ввел и широко пропагандировал арабскую систему счисления; римская же система сильно сдерживала развитие математики. Его «Книга абака» пользовалась популярностью и была переиздана в 1228 году в доработанном им виде. Абак — это счетная доска, напоминающая бухгалтерские счеты; те, кто ими пользовался, назывались «абацистами». Но под словом «абак» Фибоначчи понимал методику счета в арабской системе записи чисел без использования абака. Наооборот, он критиковал абацистов и выступал против использования абака как в теоретическом, так и в практическом отношении.

Марка с портретом Фибоначчи

Основной труд Леонардо состоит из 15 глав. Первые пять глав посвящались алгоритмам счета в арабской (он говорил в индийской) форме записи целых чисел. Здесь он критикует пифагоровы «дуги», т.е. приемы счета абацистов, рассказывает о разложении чисел на простые множители. В 6 и 7 главе рассказывается о действиях с дробями и смешанными числами. Автор учит, как приводить дроби к общему знаменателю с помощью наименьшего общего кратного. В 8 – 10 главах приводятся торгово-коммерческие задачи, основанные на пропорциях. Сюда примыкают задачи, как распределить некоторую сумму денег между членами торгового товарищества в соответствии с их долями внесенного капитала. В 11 главе приведены задачи физического содержания, например, о процентном составе сплавов из нескольких металлов. Есть задача о птицах различных видов и т.п. В 12 главе даются задачи на суммирование рядов арифметической и геометрической прогрессии. Огромному числу задач с использованием алгебраических приемов на составления систем линейных уравнений посвящена 13 глава. В 14 излагаются приближенные методы вычисления квадратных и кубических корней. Это требуется для понимания 15 главы, в которой собран обширный материал из арабских источников по решению квадратных уравнений и частных уравнений высшего порядка.

Книгу Леонардо из Пизы по доказательной силе, по широте охвата математических проблем и по важности для потомков вполне можно сравнивать с «Началами» Евклида. Математики эпохи Возрождения черпали из нее как задачи, так и приемы их решения. Долгое время они не могли превзойти гений Фибоначчи и вращались в кругу тех же самых задач, что и он, слегка изменяя их условия и модернизируя методику решения. В этом энциклопедическом издании приводилось такое огромное число задач, в том числе на прогрессии, что задача о кроликах просто затерялась. Ни автор, ни читатели его фундаментального труда никак не выделяли задачу следующего содержания. «Некто поместил пару кроликов в некоторое место, огороженное со всех сторон стенками, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения».

Задача Фибоначчи о размножении кроликов.

Задача о размножении кроликов приводит к бесконечному графу древовидной формы. Особенностью этого графа является его фрактальная природа. Это означает: какой бы узел вы не взяли в качестве корневого, весь нисходящий от него граф будет в точности повторять исходный граф с корнем в его вершине. Число узлов в графе-дереве на каждом уровне равно:

  1 13  233  4181  75025  1346269  24157817  433494437  7778742049  139583862445

  1 21  377  6765  121393 2178309  39088169  701408733  12586269025 225851433717

  2 34  610  10946 196418 3524578  63245986  1134903170 20365011074 365435296162

  3 55  987  17711 317811 5702887  102334155 1836311903 32951280099 591286729879

  5 89  1597 28657 514229 9227465  165580141 2971215073 53316291173 956722026041

  8 144 2584 46368 832040 14930352 267914296 4807526976 86267571272 1548008755920

Все это для сегодняшнего дня весьма актуально. Но, повторяем, первоначально имя Фибоначчи было прославлено вовсе не потому, что он придумал задачу о кроликах, его заслуги перед историей развития царицы наук лежат гораздо глубже. Чтобы это понять, нужно рассмотреть позиционный принцип представления чисел, на который обратил внимание Стахов, когда рассказывал о Прокле, несоизмеримости и ЗС [7].

О войне между абацистами и алгоритмистами

Люди научились считать примерно 40 тыс. лет назад. Почти повсеместно была принята десятичная система счисления (по числу пальцев рук). Племена майя, ацтеки, кельты и баски приняли за основание счета число 20 (по числу пальцев на руках и ногах). Шумерские племена по неизвестным причинам взяли за основу число 60, хотя в пределах 60 они тоже использовали десятичную систему счета. Вероятно, это объясняется использованием более продвинутой системы письменных насечек. Ее переняли вавилоняне, которые оставили после себя огромное число глиняных табличек, испещренных клинописью и разбросанных по территории Месопотамии.

Глиняная табличка с клинописью

Подобные насечки использовались всеми первобытными племенами. Сегодня их можно обнаруживают на стенах пещер, костях животных, деревянных шестах и т.д. С помощью насечек велся подсчет прошедших дней, учет убитых животных или объем собранного урожая, выраженный, например, в количестве мешков с зерном. Вместо насечек могли быть использованы палочки, природные камешки или искусственно созданные предметы, причем различной формы и окраски. Например, для отсчета единиц применялись деревянные палочки, для отсчета десятков единиц — глиняные шарики, для отсчета сотен — глиняные чашечки. Подобные инструменты, облегающие процедуру счета, назывались абаками, по-русски сказать, счеты.

Абаки — приспособления для быстрого счета

Впервые абаки начали применять в Вавилоне, а вскоре новое изобретение попало в Грецию, где получило свое дальнейшее развитие. Это приспособление представляло собой деревянную дощечку, посыпанную песком, на котором наносились бороздки. Размещенные в этих бороздках камешки обозночали числа. При этом количество камешков в первой бороздке соответствовало еденицам, во второй — десяткам, в третьей — сотням и т.д. Если в одной из бороздок набиралось десять камешков, то их снимали и добовляли один камешек в следующую бороздку.

С развитием письменных языков совершенствовалась система записи чисел. Греки, арабы и евреи для обозначения чисел использовали буквы алфавита. Такая система записи была принята большей частью народов земли. У евреев она способствовала развитию нумерологии и числовой мистики, поскольку за числами прочитывались слова, а за словами — числа. В общем, буквенная система обозначений отвечала повседневным потребностям человека, но в принципе, сдерживала развитие числовых методов расчета. Из-за этого греки больше предпочитали иметь дело с геометрией, чем с арифметикой, и развивали больше логику, чем, собственно, математику.

Особенно неудачной системой записи чисел была у римлян. Они пользовались специальной системой условных обозначений: 1 — I, 5 — V, 10 — X, 50 — L, 100 — C, 500 — D, 1000 — M. Сначала число 4 записывалось как IIII, но потом разрешено было пользоваться двумя знаками IV, что соответствовало операции вычитания 5 – 1 = 4. Число 90 = 100 – 10 можно было сокращенно записать как XC вместо LXXXX. Такая система давала преимущества для передачи информации на бумаге меньшим числом знаков, но совершенно не годилась для проведения расчетов на бумаге. Приходилась пользоваться абаком, т.е. вернуться к дописьменному инструменту ведения расчетов.

Гравюра XVI века. Мужчина ведет расчет с
женщиной с использованием абака (счетов).

Вавилонская система счисления, в отличие от всех прочих, была позиционная. Ее преимуществом было то, что одни и те же цифра, в зависимости от положения означали различные числа: 6, 60, 600, … Следующий пример записи числа 100 000 демонстрирует это преимущество.

Вавилонская система счисления

Эта форма позволила вавилонянам продвинуться далеко вперед в математике. Они знали теорему Пифагора за тысячелетие до его рождения, умели вычислять площадь круга, объемы конуса и цилиндра, лихо управлялись с дробными числами, решали системы линейных уравнений, некоторого вида квадратные и кубические уравнения. Но самое главное, они не делали из этого какого-то ажиотажа, не придавали числам мистического смысла, как это делал Пифагор, и не философствовали о гармонии мира, как это делал Платон. Для них, как и для египтян, математика была тем необходимым инструментом, который использовался точно по назначению, а именно, для решения насущных задач, связанных главным образом с числовым расчетом.

Перечисляя «три выдающихся математических открытия», Стахов назвал первым пунктом «позиционный принцип представления чисел» вавилонян. С этим невозможно спорить. Но следующим пунктом у него стоит: «несоизмеримые отрезки» [7]; речь идет о несоизмеримости, например, стороны квадрата с его диагональю. Пять или шесть тысячи лет назад вавилоняне доказали, что в этой задаче нет ничего сенсационного. Для них данный факт был как нечто само собой разумеющееся.

Вавилонская табличка

Об этом свидетельствует найденная глиняная табличка, на которой был вычерчен квадрат, сторона которого равнялась 30 условным единицам, а диагональ выражалась тремя числами — 42; 25, 36. В системе счисления вавилонян это означает, что ее длина равнялась:

42 + 25/60 + 36/60² = 42,426.

Здесь же приводилось отношение «несоизмеримых отрезков» с помощью четырех чисел — 1; 24, 51, 10. В шестидесятеричной системе счисления это означает:

1 + 24/60 + 51/60² + 10/60³ = 1,41421296;

корень квадратный из двух равен 1,41421356... Вот и получается, что для прагматичных вавилонян сторона квадрата вполне соизмерима с его диагональю. В математике существует множество не стандартных ситуаций; выделять на их фоне «проблему несоизмеримости» — значит, не видеть богатства ее многообразных форм. Во многом это раздутая философами тема, в частности, Аристотелем; ее он часто вспоминал.

После увядания античной цивилизации, математическими науками занялись индусы, которые ввели ноль и отрицательные числа. Они пользовались тоже позиционной системой счисления, что и вавилоняне, но уже на базе 10. После возникновения ислама в арабском мире сложилась благоприятная атмосфера для ведения торговли. Арабы с большой охотой воспринимали знания чужих народов, с которыми торговали. У греков они позаимствовали геометрию и астрономию, у индусов — десятеричную систему счисления и числовые алгоритмы. В десятом веке оживилась торговля с Европой.

Одним из первых выдающихся математиков Средневековой Европы был епископ Алкуин (735 – 804), уроженец Йорка. Он организовал систему школьного обучения и написал руководство «Задачи для изощрения ума юношей». При нем еще не было абаков. С развитием торговли европейские купцы стали контактировать с арабами, которые обосновались на европейской территории в Испании и на Сицилии. Французский ученый-монах Герберт (ок. 940—1003), впоследствии ставший римским папой под именем Сильвестр II, посетил Каталонию, где учился арабским премудростям и привез оттуда множество книг.

Позже им была написана книга «Правила счета на абаке», но абак, о котором писал Герберт, был заимствован не у арабов, а у римлян; числа в его книге тоже записывались римскими цифрами. Он и его ученик Рише усовершенствовали римский абак и всячески пропагандировали его достоинства. Дело дошло до того, что их обвиняли в колдовстве и общении с дьяволом, поскольку они могли производить действия с очень большими по тем временам числами.

Но вскоре в Европе появляются переводы арабских книг, в первую очередь, по арифметике, написанных аль-Хорезми (один из первых переводов сделал Фибоначчи). На латинском языке его имя звучало как Algorithmus. Отсюда пошло название «алгоритмисты» — приверженцы новой арифметики. Таким образом, начиная с XI века, в Италии и в Европе в целом стало распространяться арабская позиционная форма записи чисел, с которыми легче было работать с помощью простых алгоритмов умножения, деления, сложения и вычитания.

Индийские цифры (хинди)



Арабские цифры



Цифры арабо-индийские (габр)



Различные авторы писали арабские цифры по-разному



Форма цифровых знаков менялась со временем



Таблица перевода римских цифр в арабские

Арабы переняли цифры у хинди и называли их знаками хинди, т.е. индийскими. Европейцы эти символы заимствовали у арабов и называли их арабскими. Различные авторы писали арабские цифры по-разному; менялись они и со временем. В итоге, арабские знаки имели две формы записи — восточную и западную, которые заметно отличались друг от друга. Западная форма индийско-арабских цифр получила название «габр» (ghubr).

Трудно сейчас представить, какая ожесточенная война разразилась между «абацистами», которые использовали абаки Герберта и римскую систему записи, и «алгоритмистами», приверженцами арабской (точнее, индийско-арабской) системы записи чисел, предпочитавшими вести расчеты на бумаге. Церковь и государственные чиновники продолжали пользоваться системой, оставшейся в наследство от Римской империи, а математики и прочие ученые, а также деловой и торговый люд быстро перешли на новую, как быстро выяснилось, более прогрессивную форму счета.

Символом абацистов был Пифагор, который, по их мнению, пользовался абаком и римской системой записи чисел. Символом алгоритмистов был Боэций: считалось, что он, сидя в тюрьме, не имел под рукой абака и все расчеты производил на бумаге, используя позиционную запись чисел.

Сохранилась гравюра 1512 года, на которой изображены три персонажа: по центру богиня-аллегория Арифметика, справа от нее сидит новатор Боэций, делающий записи арабскими цифрами, а слева — консерватор Пифагор, считающий на абаке (сбоку на лентах написаны их имена). Богиня Арифметика явно благоволит Боэцию, у нее на платье видны арабские числа.

Гравюра Грегори Райша (Gregor Reisch) 1512 года, Страсбург.

Война между абацистами и алгоритмистами шла тяжело и неприлично долго. Достаточно сказать, что монеты с арабскими цифрами впервые появились в Швейцарии в 1424 году, в Германии — в 1458, во Франции — в 1485, а в консервативной Англии — лишь в 1551 году. В Европе алгоритмисты окончательно победили после Французской революции, когда арабскую символику ввели правительственным декретом 1789 года. Тех, кто продолжал использовать символику римскую и пользовался абаком, революционное правительство сурово наказывало. В Азии этот процесс затянулся еше сильней. Так, советские бухгалтера и продавцы магазинов пользовались счетами, т.е. абаками, вплоть до появления калькуляторов.

О числах Фибоначчи, филлотаксисе и ЗС

В предыдущем разделе было показано, что выделенное Стаховым второе выдающееся открытие в области математики, несоизмеримость отрезков, является вполне рядовой задачей. Нахождение объема конуса или решение кубического уравнения для науки было ничуть не менее важным событием. А что же с третьим пунктом списка открытий, с золотым сечением? Увы, оно вообще никак не сказалось на развитии математики. Слова Стахова, что «Кеплер, в отличие от тех математиков, которые его критикуют, был не только гениальным астрономом, но и гениальным математиком» [7] не находят никакого фактического подтверждения. В области математики он практически ничего не сделал, так что его хвалебные слова по поводу ЗС лишний раз подтверждают, что мистически настроенный астроном находился в стороне от магистрального направления развития математической науки.

Краткий обзор развития математики во время Ренессанса и вскоре после него сделан мною раньше (см. раздел Конструктивная алгебра). Из него видно, что главной проблемой для европейских математиков, а до этого арабских, было решение алгебраических уравнений. Именно эта задача двигала математику вперед. Затем появилась полноценная наука физика и математика переключилась на решение физических задач.

На сайте Sceptic-Ratio имеются еще несколько страничек, где вопросам истории математики отведено немало места. Например, раздел Геометрия и опыт: Гаусс, Риман, Клейн, Пуанкаре посвящен сравнительно недавнему открытию многомерной и дифференциальной геометрии, а раздел Реконструкция математического мышления древних, напротив, переносит нас в седую старину.

Чтобы убедиться, что ЗС сыграло ничтожную роли в развитии математики, достаточно полистать трехтомник «История математики с древнейших времен до начала XIX столетия» под редакцией А.П. Юшкевича [9]. Хорошо, если в нем в общей сложности наберется страничка текста, где рассматривается данный вопрос. Без позиционного счета не было бы математики; выброси из математики глупости на почве ЗС и она ничего не потеряет, напротив, только очистится от лишнего балласта.

Таким образом, невозможно даже сравнивать ожесточенную войну между абацистами и алгоритмистами с жалкими попытками гармонистов-золотоискателей обратить на себя внимание. Математики калибра Фибоначчи, Кардано, Виета, Декарта, Гаусса, Эйлера, Даламбера, Клейна прошли мимо их мистических переживаний. Наоборот, тот, кто занимается вопросами гармонии и ЗС — касается ли это музыки, изобразительного искусства, кристаллографии и т.д. — сразу вызывает подозрение у профессионалов. Специалист интуитивно распознает в нем дилетанта и спешит как можно скорее избавиться от его навязчивых предложений.

Мы были свидетелями, как каббалист-золотоискатель Мельхиседек сочинил насквозь лживую историю про «монаха» Фибоначчи, который «часто пребывал в состоянии медитации», «любил прогуливаться по лесам и медитировать во время прогулок». Своим левым полушарием он якобы «начал замечать, как растения и цветы содержат в себе числовые соответствия» и т.д. [3].

Разумеется, ничего подобного не было. Фибоначчи был до мозга костей рационалистом. Разъясняя решение задачи о кроликах, он выписал несколько членов известного нам числового ряда, но дальше и пальцем не пошевелил, чтобы установить связь его с ЗС. Впервые это сделал даже не Лука Пачоли, а малоизвестный немецкий математик Симон Якобс Рехенбух (1510 – 1564) из Франкфурта-на-Майне. На полях страницы 48 своего сочинения он выписал 27 членов числовой последовательности Фибоначчи и установил связь ее с числами Ф и φ. Он также обнаружил закономерность между тремя соседствующими членами ряда:

F²(n) – 1 = F(n – 1) × F(n + 1).

В этом ряду Фибоначчи Симоном Якобсоном Рехенбухом
допущена описка: вместо числа 13 здесь стоит число 15.

Что касается связи чисел Фибоначчи с филлотаксисом, т.е. с количеством и расположением зерен в сосновых шишках, семечек в корзинке подсолнуха, лепестков у цветов, листьев и веток у растений, то это произошло много позже. В конце 18-го – в начале 19-го вв. естествоиспытатели Шарль Бонне (1720 – 1793) и братья Браве (1937) взялись подсчитывать и описывать объекты своих ботанических исследований и наткнулись на любопытную закономерность. При этом их головы были свободны от того мистического наваждения, которым Мельхиседек одарил сознание Фибоначчи. Поэтому нет ничего удивительного в том, что этой вполне научной задачей в 19-м столетии заинтересовались многие адекватно мыслящие ученые. Однако у современных золотоискателей 21-го века, даже скептически настроенных к учению Стахова, при слове «филлотаксис» возникает какое-то трепетное чувство.

Филлотаксис: в данном случае это расположение
семян в соответствии с числами Фибоначчи.

Из всех критиков Стахова наиболее здравую позицию выбрал, пожалуй, Радзюкевич. Подобно Белянину и Василенко он сначала симпатизировал учению о гармонии, ЗС и числах Фибоначчи, но потом отверг его религиозно-мистическую составляющую. В статье [10] приведены его слова: «Мое отличие от сторонников ЗС заключается в отсутствии "священного трепета" перед ЗС. В свое время я натрепетался перед ним. Затем протрезвел. Мне кажется, что ряд сторонников ЗС находятся в некотором священном опьянении». Эти слова взяты из письма Радзюкевича Стахову. В другом письме к нему Радзюкевич пишет: «…Когда я был студентом и читал Ваши работы, считая их прорывом, то даже и не мог подумать, что через 20 лет смогу вступить с Вами в полемику» [11].

В полемике со Стаховым Радзюкевич категорически отказывает ему в праве распространять golden ratio на предметы искусства: «архитектуроведение и искусствоведение являются тоже науками (в том числе и история), может быть менее "серьезными", чем математика и физика, но все же науками с определенной методологией и спецификой. И когда некоторые представители "серьезных" и "глобальных" наук залетают в эту сферу и сходу находят в ней "золото", то у меня возникает потребность в том, чтобы их поправить» [11].

Доводы Радзюкевича следующие: «в произведении искусства — главное — образ. Его измерить ничем невозможно. Это тайна, недостижимая ни для какой науки. Если же брать процесс проектирования предметов и среды, то здесь, вероятно, ЗС даст возможность найти оптимальные решения в каких-то ситуациях. Но эти ситуации необходимо моделировать и рассчитывать, а не просто накладывать на лист золотой прямоугольник или треугольник. Инженерный расчет несущей балки вряд ли покажет, что ЗС является оптимальной пропорцией сечения» [11].

Эта аргументация, кажется, убедила Стахова. «Я согласен с Вашими рассуждениями», — написал он Радзюкевичу 27 февраля 2006 года. Редакция сайта «Академия Тринитаризма» тоже признала победу Радзюкевича в полемике со Стаховым. «Главный итог дискуссии состоит в следующем. Необходимо различать "Законы Гармонии в Природе" и "Законы Красоты в Искусстве". Это — не одно и то же. Раскрытие "Законов Гармонии Природы" есть, по большому счету, главная задача науки. Последние достижения в этой области показывают, что Золотое Сечение и числа Фибоначчи играют фундаментальную роль в "Законах Гармонии Природы" — и этот подход может привести к новым идеям в развитии фундаментальных наук (математики, физики, биологии и т.д.), — и в этом отношении проф. Стахов, безусловно, прав. На данном этапе Золотое Сечение является мощным фактором научного и экономического развития. И чем раньше это осознает большинство представителей "точных наук", прежде всего, математики, теоретической физики, экономики, тем быстрее древнейшая научная парадигма сможет внедриться в современную науку и образование. С другой стороны, "Законы Красоты Искусства" носят в большей степени качественный, чем количественный характер и не сводятся к Золотому Сечению, хотя Золотое Сечение все же играет в Искусстве определенную роль. И в этом отношении прав архитектор А. Радзюкевич» [11].

В этом тексте я выделил курсивом экономику. Имея в виду эту науку, золотоискатели ссылаются на действие в экономике волнового принципа Эллиотта, о котором мы поговорим позже. Прежде чем начать разговор о природе (или Природе, если угодно), скажем, что Радзюкевич всё-таки разорвал всякие отношения с «Академией Тринитаризма» и золотоискателями вообще. В заметке от 1 сентября 2006 года он написал: «Очень прошу членов Института Золотого сечения больше не обращать внимания на мои тексты. Я думаю, что у Вас есть гораздо более важные и интересные дела. Будем считать, что вы разгромили меня окончательно и бесповоротно» [12].

Еще до «дружеского рукопожатия» Радзюкевич свободно шел на разрыв со Стаховым, но тот дипломатично ушел от разрыва: «Если Вы с Вашими соратниками находите "золото" везде, то из этого не следует, что метод "нащупывания золота" является единственно верным во всех сферах знания. … Я сделал для себя выводы из этого общения и полагаю, что пора закругляться. Боюсь только того, что, в конце концов, Вы достигните такого момента в развитии своей науки, когда в мире не останется ни одного объекта и ни одного явления, не увязанного Вами с золотом» [13].

После публикации статьи Радзюкевич «Красивая сказка о "золотом сечении"» на сайте СибДИЗАЙН.ру развернулась дискуссия. В посте от 13.08.2002 Радзюкевич написал: «Разумеется, я допускаю мысль, что в каких-то научных сферах могут быть найден и доказаны научно (!) особые свойства "золотого сечения". В частности, есть ряд работ по закономерностям воздушного давления в помещениях. Есть работа медика Цветкова об особенностях работы сердечной мышцы. Есть, в конце концов, закон филлотаксиса. Может быть, там что-то и есть, а может быть, и нет. Проблема заключается в том, что большинство убеждено, что есть и есть везде. Я ставлю это под сомнение» [14].

По-видимому, Радзюкевич тесно увязывает числа Фибоначчи, появляющиеся в филлотаксисе, с ЗС. Малыгин Александр Георгиевич от 24.02.2004 написал ему: «я решительно не согласен с отрицанием проявления ряда Фибоначчи, а следовательно, и отношения золотого сечения, в филлотаксисе. Это легко наблюдаемый факт». Радзюкевич отвечает Малыгину: «По поводу филлотаксиса полностью с Вами согласен. Это факт безусловный. В момент написания этой статьи я полагал, что этот факт имеет только эмпирическое подтверждение. В прошлом году я попытался более детально разобраться в этой проблеме (Щетников А.И., Радюк М.С, Cohn D, Douade S., Couder Y)» [14].

Всякий раз, когда кто-то заводил разговор о ЗС и увязывал его с филлотаксисом, т.е. с числами Фибоначчи, Радзюкевич без всяких колебаний соглашался с ним. Мечислав Радюк в своем посте от 12.04.2004 написал: «Природа во всех своих проявлениях стремится к экономии. В частности — через максимально простые способы решения своих задач. Эта простота может достигаться повторением одного и того же удачного приема, приводящего к появлению фрактальных (самоподобных) структур и процессов. Во многих случаях это возможно, только при золотой пропорции между частями целого (филлотаксис), либо закономерно приводит к ней (что моделируется максимально простым способом построения ряда Фибоначчи). Отсюда предположение, что оптимальность золотого сечения связана с присущим ему свойством самоподобия (минимум отношений между целым и его частями)». Радзюкевич ответил на это: «По поводу филлотаксиса я с Вами не спорю» [14].

Примечательно, указывая на «сферы приложения гипотезы "золотого сечения"», Радзюкевич называл не фуллерены и квазикристаллы, а только филлотаксис: «В биологии она подтверждается на фактах (филлотаксис)» (пост от 23.07.2005) [14]. Видимо, Радзюкевич ничего не знает о фуллеренах и квазикристаллах, поэтому и не приводит их в качестве подтверждения существования ЗС в природе. Стахов же, находясь на одном уровне компетентности с Радзюкевичем, тем не менее, ставит фуллерены и квазикристаллы на первое место как представителей трансцендентного мира Гармонии.

Не испытывая более «священного трепета» перед ЗС, Радзюкевич, однако, сохранил в душе смутное ощущение, что ЗС через числа Фибоначчи проявляет себя в филлотаксисе. Стахов знает, но никогда не скажет своему врагу Радзюкевичу, что ЗС и числа Фибоначчи, с точки зрения математики, это две большие разницы.

Возьмите два произвольных числа — пусть ими будут 6 и 51 — и подвергните их той же самой процедуре, которой подвергаются числа Фибоначчи. В результате получится ряд:

6   51     57     108     165     273     438     711     1149     1860     3009 …     (10)

Если теперь составлять отношения из смежных чисел, то получится ряд, который сходится к ЗС:

51/6 = 8,5    57/51 = 1,112    108/57 = 1,895    165/108 = 1.52

273/165 = 1.654        438/273 = 1.604        711/438 = 1.623

1149/711 = 1.616     1860/1149 = 1,619     3009/1860 = 1,618

Этот простой числовой пример доказывает, что ЗС порождается процедурой получения членов числового ряда и не имеет никакого отношения к самим числам Фибоначчи, представленными рядом:

1     1     2     3     5     13     21     34     55     89     144     233     377     610     (11)

Поэтому, если обожествили ряд Фибоначчи (11), то обожествлять нужно не только числа (10), но и всё бесконечное многообразие чисел, так как они все могут участвовать в подобных процедурах — ведь числа 6 и 51 мы взяли произвольно.

Тогда почему числа ряда (11) появляются при филлотаксисе, а числа ряда (10) в ботанике никто не встречал? Потому что рост количества семечек в подсолнухе или зерен в сосновой шишке начинается всегда с единицы. Поэтому, если не будет никаких сбоев при «взрослении» подсолнуха и шишки, мы всегда будем получать ряд чисел Фибоначчи (11).

Математический алгоритм заполнения корзинки подсолнуха семечками совпадает с алгоритмом Евклида по нахождению наибольшего общего делителя двух чисел a и b — НОД(a, b). Напомним, его идея сводится к последовательному вычислению следующих равенств:

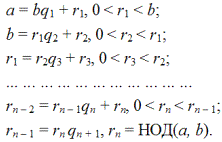
Отношение a / b можно представить в виде цепной дроби. Чтобы к ней перейти, нужно разделить все равенства, полученные в алгоритме Евклида, на b, r₁, r₂, ..., r_{n –1}, r_n, получим:

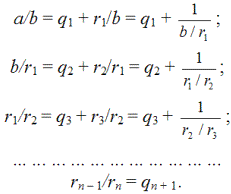
Последовательно подставляя эти равенства друг в друга, получаем цепную дробь, например:

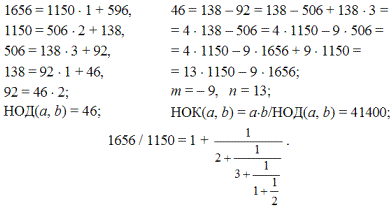
Бесконечная цепная дробь для Ф предполагает, чтобы все q_i = 1 :

«Золотым» числам Ф и φ соответствуют углы 222°29'32" и 137°30'28". В статье Щетникова [15] имеется рисунок, рассчитанный по алгоритму Евклида для корзинки, вмещающей 1000 семечек; воспользуемся им. При угле φ попарно образуются встречные дуги с числами Фибоначчи — (34, 21), (55, 34), (89, 55).

Корзинка подсолнуха, число семян = 1000, φ = 137°30'28"

На рисунке мы видим, как скачкообразно происходит изменение направления и числа дуг, отвечающих смежным числам Фибоначчи (34, 21), (55, 34), (89, 55). Это связано, очевидно, с тем, что алгоритм Евклида порождает рекурсию, а она, в свою очередь, определяет фрактальное строение корзинки с семечками. Фрактальные структуры содержат аттракторы, т.е. точки притяжения, в которых происходит смена направления протекания процесса. Числовые значения (34, 21), (55, 34), (89, 55) как раз и соответствуют таким аттракторам.

В 1963 году Лоренцем был открыт аттрактор, получивший название «странный». Его вид напоминает бабочку; при возрастании аргумента t функция x (t) периодически перепрыгивает то на одно крыло бабочки, то на другое. В процессе заполнения корзинки с семечками происходит нечто похожее.

Странный аттрактор Лоренца
(для увеличения рисунка нажмите на него)

Малейшее отклонение угла φ от значения 137°30'28" приводит к радикальной смене упаковки семян. В этой упаковки семечки находятся не в одинаковом положении относительно своих соседей, т.е. одни семечки имеют большее «жизненное пространство», другие меньшее. По-видимому, такая структура не является жизнеспособной и в природе не реализуется.

Три упаковки семян при трех различных углах φ;
две крайние упаковки не выгодны для выживания семян.

Зато в природе можно найти две равномерных упаковки, показанные на следующем рисунке, которые реализуются при углах 99,5° и 77,9°. Они отвечают рядам Фибоначчи, соответственно, 1, 3, 4, 7, … и 1, 4, 5, 9, 14, … и записываются цепными дробями вида 1 / (3 + φ) и 1 / (4 + φ).

     

Две равномерные упаковки семян при углах 99,5° и 77,9°

Так как две последние фрактальные упаковки семян встречается реже, то первая упаковка для угла φ является, видимо, оптимальной с точки зрения выживания. Сосновые шишки имеют около 100 чешуек (зерен), которые распределены по 8 "правым" ветвям и 13 "левым". Причем каждая чешуйка, имея четыре стороны, соседствует с четырьмя другими чешуйками. У ананаса имеется не две, а три спиральных дуги с числами Фибоначчи 5, 8 и 13, так что каждая его гексагональная чешуйка соседствует уже с шестью другими чешуйками. Как видим, филлотаксис подчиняется простым математическим закономерностям. Упаковка семян в ананасе и шишке равномерно плотная. Эта оптимальная конфигурация обеспечивается свойствами чисел Фибоначчи. Для ананаса этот факт очевиден: ему нужно, чтобы выполнялось условие 13 = 8 + 5, если вместо 8 рядов будет 9, то возникнет противоречие.

           

Числа Фибоначчи: ананас (5, 8, 13) и сосновая шишка (8,13)

Авторы статьи [16] решили упорядочить элементы Периодической таблицы Д.И. Менделеева в соответствии с упаковкой семян подсолнуха. Они пишут: «Одна из идей, направленных на совершенствование периодической системы Д..И. Менделеева сводится к поиску путей сближения элементов по всем направлениям… Очевидно, изображать атомы в системе следует в виде самых симметричных фигур, какими являются круг на плоскости или шар в пространстве» [16].

Таблица химических элементов [16]

Такой подход выглядит искусственным, так как филлотаксис ориентируется на равномерность расположения семян или листьев растений. Вряд ли можно предположить, что философия «выживанием» лежит в основе химических элементов. Между тем, один из авторов потратил на составление данной таблицы 40 лет своей жизни и сильно подорвал здоровье. Каким отделом мозга он при этом думал, догадаться не сложно. Очевидно, такого рода задачи относятся к классу задач о Нефертити.

---

1. Стахов А.П., Садченко Е.В., Егорова-Гудкова Т.И. Математика Гармонии и Современная Наука. Учебник по курсу «Математика Гармонии» для студентов физико-математических, инженерных и экономических специальностей / Под редакцией доктора технических наук, проф. Стахова А.П.— 2010.
2. Ньютон И. Математические начала натуральной философии. — М., 1989.
3. Друнвало Мельхиседек. Древняя тайна Цветка Жизни. Т. 1,2. Издательство: София, 2009 г. — 320 с. / The Ancient Secret of the Flower of Life. Vol. 1,2. / www.webbl.ru.
4. Савельев С.В. Происхождение мозга. — М.: ВЕДИ, 2005.
5. Голдберг Э. Управляющий мозг: Лобные доли, лидерство и цивилизация. — М.: Смысл, 2003.
6. Стахов А.П. Гармония Мироздания и Золотое Сечение: древнейшая научная парадигма и ее роль в современной науке, математике и образовании. Часть 1,2 //«Академия Тринитаризма», М., Эл № 77-6567, публ.12840, 19.01.2006.
7. Стахов А.П. Конец или начало новой науки? http://goldensectionclub.blogspot.com/2010/05/blog-post_21.html.
8. Евклид. Начала. — Киев, 1880.
9. История математики с древнейших времен до начала XIX столетия (в 3-х томах). Под редакцией А.П. Юшкевича. Т.1. — М.: Наука, 1970.
10. Стахов А.П. «Золотое Сечение» как важный фактор научного и экономического развития (ответ на письмо А. Радзюкевича).
11. Алексей Стахов, Андрей Радзюкович. Дружеское рукопожатие // «Академия Тринитаризма», М., Эл № 77-6567, публ.13042, 02.03.2006.
12. Радзюкевич А.В. В который уж раз о золоте (ответ непонятно кому и непонятно зачем) // «Академия Тринитаризма», М., Эл № 77-6567, публ.13741, 01.09.2006.
13. Радзюкевич А.В. Я не хочу с Вами спорить - ответ А.П. Стахову // «Академия Тринитаризма», М., Эл № 77-6567, публ.13010, 22.02.2006.
14. Радзюкевич А.В. Дискуссия на сайте СибДИЗАЙН.ру после публикации статьи Радзюкевич «Красивая сказка о "золотом сечении"».
15. Щетников А.И. Проблема филлотаксиса (Phyllotaxis.pdf).
16. Н.А. Шило, А.В. Динков, Фенотипическая система атомов в развитие идей Д.И.Менделеева // «Академия Тринитаризма», М., Эл № 77-6567, публ.14630, 09.11.2007.