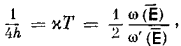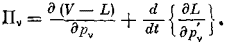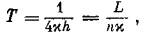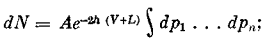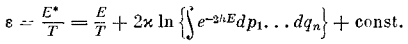Квантовая механика: её история и суть

Олег Акимов

Милева Марич — мать квантовой механики

• Эйнштейн против Эйнштейна?
• Зарисовка с милого юноши
• Его трудности с математикой
• Больцмана не читал, но с ним не согласен
• Альберт: некогда мне заниматься физикой
• Первая статья Эйнштейна — Марич
• Вторая статья Эйнштейна — Марич
• Третья статья, написанная одной Марич
• Четвертая статья, написанная одной Марич

Эйнштейн против Эйнштейна?

Нет никаких сомнений в том, что отцом квантовой механики является Макс Планк. 19 Октября 1900 года на заседании Берлинского физического общества он сделал доклад, где предложил формулу распределения энергии в спектре черного тела, полученную на основе гипотезы квантов. Традиционно принято считать, первым, кто оценил и продолжил разработку его идеи, был Альберт Эйнштейн. 18 марта 1905 года редакция «Annalen der Physik» получила его статью «Об одной эвристической точке зрения, касающейся возникновения и превращения света», в которой ряд оптических явлений объяснялся с помощью световых квантов.

Революционная идея его статьи заключалась в новом взгляде на распространение света; она вводила корпускулярный физический объект, впоследствии названный фотоном. До сих пор явления интерференции и дифракции свидетельствовали о волновой природе света. Она предполагала наличие эфира как сплошной светоносной среды, которая выполняла ту же роль для звуковых волн, что и воздух. И вот никому неизвестный молодой автор указал на явления, скрупулезно изучавшиеся Максом Планком, Филиппом Ленардом и Иоганнесом Штарком, которые позволяли говорить о свете как о крохотных частицах, летящих в абсолютно пустом пространстве. В преамбуле к статье он написал:

«Я и в самом деле думаю, что опыты, касающиеся "излучения черного тела", фотолюминесценции, возникновения катодных лучей при освещении ультрафиолетовыми лучами и других групп явлений, связанных с возникновением и превращением света, лучше объясняются предположением, что энергия света распределяется по пространству дискретно. Согласно этому сделанному здесь предположению, энергия пучка света, вышедшего из некоторой точки, не распределяется непрерывно во все возрастающем объеме, а складывается из конечного числа локализованных в пространстве неделимых квантов энергии, поглощаемых или возникающих только целиком. Ниже я излагаю ход мыслей и факты, натолкнувшие меня на этот путь, в надежде, что предлагаемая здесь точка зрения, возможно, принесет пользу и другим исследователям в их изысканиях» [1, т. 3, с. 93].

С введением фотона в физике сложилась парадоксальная ситуация, характеризующаяся противоречивым термином дуализм волны-частицы. Она требовала от теоретиков взаимоисключающих представлений, которые привели к тотальной формализации физики. Отныне главный инструмент теории познанья — пространственно-механический образ — был изъят из обращения самой развитой отрасли знаний об окружающем нас мире; его место занял символ. В результате этой далеко неравноценной подмены некогда передовая наука начала быстро увядать и погружаться в трясину романтической схоластики. В неё ринулись люди, по природе своего ума совершенно не предназначенные для рациональной научно-исследовательской работы. По поводу модельных вихрей и других пространственных механизмов они с возмущением и призрением вопили: «Нам не нужны декартовские представления о мире! Мы познаем его с помощью одних только уравнений». Вместе с тем в своей фантастической космологии они ввели столько извращенных геометрических форм наподобие черных дыр, что всякая античная мифология меркнет перед их чудовищными видениями. Таким образом, вакуум, принесенный фотонной теорией и теорией относительности, опустошил физические представления в прямом и переносном смысле.

Макс Борн

Ровно через полвека, 18 марта 1955 года, на заседании всё того же Берлинского физического общества Макс Борн сделал доклад на тему «Альберт Эйнштейн и световые кванты», в котором произнес следующие слова:

«В промежуток времени между 1900 и 1905 гг. теория квантов, по-видимому, не сделала никаких успехов. Также и в основательной и широко охватывающей книге Э. Уиттекера «История, эфира и электричества» (1953), недавно вышедший второй том которой охватывает период с 1900 по 1926 год, ничего не сообщается об этом периоде.

Иная картина возникла, когда 50 лет назад появилась первая работа Эйнштейна (Ann. Phys. 17, 132, 1905). Первые шесть параграфов этой работы содержали теоретические соображения, которые, за исключением немногих специалистов, привлекли к себе мало внимания. Однако последние три параграфа были посвящены совершенно новым применениям квантов, а именно — к объяснению правила Стокса при люминесценции, к фотоэлектрическому эффекту и к ионизации газов. Общая точка зрения состояла в том, что во всех этих случаях речь идёт о превращении кинетической энергии Е электрона в световой квант hν или наоборот, так что должно иметь место линейное соотношение вида

Е = hν + const.

Это соотношение на диаграмме (Е, ν) представляется в виде прямой с наклоном h, где h — универсальная постоянная Планка, значение которой было определено Планком из измерений излучения. Таким образом, это были доступные экспериментальной проверке утверждения и нет ничего удивительного в том, что физики-экспериментаторы на эту проблему набросились» [2, с. 121 – 122].

Продолжение этого доклада читайте в разделе Борн против Эйнштейна.

Коллаж из двух фотографий 1896 года, когда
Альберту Эйнштейну 17 лет и Милеве Марич 21 год.

Гордые, важные мужья не станут говорить о пресмыкающихся перед ними жёнах. В силу этого мы ничего не знаем о супруге Борна или Планка, зато с недавнего времени мы неплохо представляем себе первую жену Эйнштейна. Это она, волевая и целеустремленная 21-летняя девушка, взяла за руку слабовольного и безалаберного 17-летнего юношу и повела его уверенной поступью в величественный Храм Науки. Из раздела Милева Марич как подруга и жена Эйнштейна мы уже знаем, какими интеллектуальными способностями обладала эта девушка, а из раздела Эйнштейн в детские и молодые годы мы также знаем, что представлял собой этот самоуверенный, не блещущий особыми талантами, юноша. Для лучшего понимания главной идеи данного раздела ниже широкими мазками будет нарисован небольшой эскиз любимого персонажа иконописи ХХ века. Но не этот реалистический набросок станет нашим главным звеном в цепи доказательств, кого нужно считать истинным продолжателем квантовой идеи Планка. Для понимания руководящей и направляющей роли первой жены Эйнштейна в деле написания научных статей мужа нужно тщательно изучить и сравнить содержание всех публикаций, написанных до и после их брачного развода. А это большой и кропотливый труд, который не может быть окончательно завершен настоящей статьей. Отсюда ее предназначение, скорее, в том, чтобы пунктирными линиями обозначить основные направления такого всестороннего анализа.

Аналогичный подход был использован при доказательстве мошеннической натуры Зигмунда Фрейда. В основе его научной деятельности лежал обман (см. Сущность фрейдизма). В разделе Как возник психоанализ была проанализирована книга «Исследование истерии», написанная им совместно с врачом-физиологом Йозефом Брейером. В результате детального сравнения текстов двух авторов удалось убедительно доказать аморальную и ненаучную позицию первого психоаналитика. Дальнейшее изучение его сочинений, в первую очередь «Толкование сновидений», позволило узнать истинную Правду о Фрейде и психоанализе. Социально-психологические механизмы раскрутки имени Фрейда ничем принципиальным не отличаются от механизмов раскрутки имени Эйнштейна. Оба кумира ХХ века были порядочными прохвостами, которые перед газетными репортерами умело разыгрывали из себя больших ученых, не являясь таковыми на самом деле (в разделе Начни с Фрейда, чтобы лучше понять Эйнштейна об этом кое-что было уже сказано). Тем не менее за ними устремились толпы восторженных почитателей, которые с пеной у рта стали убеждать оставшееся в недоумении население в их неподражаемой одухотворенности. В течение последующих десятилетий произошла интституализация и канонизация эйнштейнианства по мощи превосходящее фрейдизм. Отцы новых вероучений приобрели ореол мученичества, воспетый хорами обеих церквей. Наиболее рьяные служители культов, бесконечно пересказывая и толкуя священные мифы, всё ещё пользуются в массовом сознании благоговейным авторитетом.

Коллаж: 1896 год, переезд Милевы Марич
из сербского города Новый Сад (слева)
в швейцарский город Цюрих (справа).

При сравнении работ, написанных с Милевой Марич и без нее, надо обратить внимание прежде всего на стиль написания трех статей, непосредственно предшествовавших главной статье по квантовой механике — «Об одной эвристической точке зрения, касающейся возникновения и превращения света» (1905, статья 7). Этими статьями являются «Кинетическая теория теплового равновесия и второго начала термодинамики (1902, статья 3), «Теория основ термодинамики» (1903, статья 4) и «К общей молекулярной теории теплоты» (1904, статья 5). Здесь в круглых скобках указан год издания в «Annalen der Physik» и порядковый номер статьи в «Собрании научных трудов» Эйнштейна [1, т. 3]. Так вот, главной отличительной чертой всех перечисленных статей является даже не их сугубо математический характер, чуждый Эйнштейну, а статистический дух модели, навеянный трудами Больцмана по кинематической теории газов. Этот вероятностный подход к объекту исследования в 1926 году будет подвергнут Борном и его сподвижниками, Гейзенбергом и Бром, дальнейшей релятивизации, т.е. усилением формально-спекулятивного компонента в интерпретации движения фотона и электрона (см. Борн против Эйнштейна). Эйнштейн же категорически запротестовал против статистической интерпретации волновой функции и до конца своих дней с жаром отстаивал детерминистский взгляд на динамику субатомного мира (см. Альберт Эйнштейн против квантовой механики).

Милева Марич и Альберт Эйнштейн
с сыном Гансом-Альбертом, 1905 год

В связи с этим историки науки в один голос заявляют о будто бы глубокой трансформации его мировоззрения. Действительно, выглядит весьма странно, когда человек, якобы предложивший статистическую модель излучения и поглощения света, с какого-то момента меняет свое мировосприятие на диаметрально противоположное и с упорством твердолобого марксиста практически во всех своих публичных выступлениях доказывает одно и то же: я верю в построение детерминистской теории атомов, статистическое описание реальности — неполно. И это притом, что весь статистический аппарат термодинамики только и был введен потому, что координаты, начальные скорости и направления движения всех молекул газа никогда не будут нам известны. Это принципиальное условие неопределенности сохраняется в квантовой механике и его невозможно обойти, находясь в рамках современной спекулятивной картины мира. Об этом Эйнштейну без конца твердили его коллеги по созданию формалистских концепций. Поэтому, естественно, у внимательного исследователя данной историко-психологической ситуации тут же возникает вопрос: а он ли был автором статистических работ, включая знаменитую статью 1905 года?

Давайте проследим за основными этапами трансформации взглядов удивительного автора, которого можно было бы условно назвать Марич—Эйнштейн. С этой целью набросаем обещанный выше портрет молодого человека, имя которого нам хорошо известно — Альберт Эйнштейн. Его уныло серый образ поместим на сияющем фоне Милевы Марич. Не станем заглядывать в слишком далекое детство; начнем с периода времени, когда оба наших героя погрузились в радужную атмосферу научных исканий.

Зарисовка с милого юноши

После далеко неблестящего окончания Политехникума (июль 1900 года) Альберта никуда не взяли. Два года он болтался без дела, изредка прирабатывая частными уроками. Отец Марселя Гроссмана (его сокурсник, товарищ и впоследствии помощник-математик) раздобыл ему местечко в Патентном бюро Берна, куда он выехал в конце февраля 1902 года, но приступил он к работе только в середине июня. Из дюжины работников этой конторы Альберт занимал самую низшую должность (служащий 3-го разряда), имел самую низкую ставку (3500 франков в год), причем неприлично длительное время он работал в Бюро на птичьих правах, т.е. без контракта: его испытательный срок закончился лишь в середине сентября 1904 года. За весь период работы в конторе (он уволился в середине октября 1909 года) Альберт поднялся лишь на одну маленькую ступень выше, до второго разряда с окладом в 4500 франков в год. Это знаменательное для него событие произошло на четвертом году его пребывания в конторе, а именно, 1 апреля 1906 года.

Альберт и Милева в начале, середине и конце своей совместной жизни.

Милева обожала Альберта и мечтала о его профессорской карьере, но муж от звонка до звонка 8 часов в день протирал штаны в патентной конторе, а воскресные дни беззаботно проводил с друзьями. Из-за национальных предрассудков родители-евреи всячески противились женитьбе их смазливого и самоуверенного чада на «безобразной сербке», этом «книжном черве», как со злорадством говорила мамаша бесхарактерного паренька. Однако волевая и упорная Милева всё же рассчитывала на нисхождения: если она поможет Альберту защитить докторскую диссертацию, быть может, его родители сжалятся и согласятся на их брак. Поэтому день и ночь она трудится над научными статьями для этого ленивого и безалаберного сыночка, у которого на уме одни только романтические глупости.

На себя она давно махнула рукой: неудача с дипломом, дети и хлопоты по дому поставили крест на ее научной карьере. Началось всё в зимний семестр 1897/1898, когда Милева уехала в Гейдельбергский университет для получения свежих знаний с передового фронта науки. Ее возвращению в Политехникум не больно-то обрадовались тамошние преподаватели. Они восприняли эту поездку в немецкий Храм Науки как оскорбительную пощечину. В итоге, она так и не смогла войти в нормальный ритм учебы. Некоторые преподаватели были к ней очень необъективны и это притом, что многие дисциплины ей пришлось изучать самостоятельно.

Политехникум в Цюрихе (ETH), в котором учились
Альберт Эйнштейн и Милева Марич с 1896 по 1900 год.

Как раз на этот период приходятся ее непростые отношения с Альбертом, который увлекся другими девушками, а его мать периодически закатывала громкие скандалы. Всё это сильно мешало учебе, поэтому экзамены она сдала неважно. И хотя свидетельство об окончании Политехникума девушка получила, право преподавать — нет. Однако мучавший ее преподаватель Вебер, по достоинству оценив ее интеллектуальные способности, принял в докторантуру Цюрихского университета для продолжения научной работы. Мечтая заняться наукой на пару с будущим мужем, она попросила декана Вебера взять на ставку ассистента Альберта. Тот категорически отказался, будучи уверенным, что из этого лоботряса никогда не получится добросовестного исследователя. Милева обиделась за своего возлюбленного и хлопнула дверью.

На смертном одре отец благословил брак Альберта с Милевой и через три месяца, 6 января 1903 года, они поженились. Еще до замужества, в январе 1902 года, она родила от Альберта девочку, которую отвезла к своим родителям в Новый Сад. В сентябре 1903 года девочка умерла. В середине мая следующего года у них родился сын. Именно с его рождением было связано зачисление никудышного работника в списочный штат Патентного бюро.

Марсель Гроссман и Альберт Эйнштейн.

Почему его не ценили в конторе — более чем понятно. Юноша витал в облаках, мнил себя великим изобретателем электрических машин, которыми он увлекся еще в детстве, когда посещал электромастерскую отца и дяди. Герман и Яков Эйнштейны пытались наладить производство электромоторов, но успешного бизнеса у них не получилось. Тяга Альберта к техническому творчеству определила его поступление в Политехникум, а потом выбор работы в техническом бюро патентов. Его родители надеялись, что из их непутевого отпрыска когда-нибудь получится путевый инженер-изобретатель. Но Милева видела в своем избраннике не технического эксперта, а прославленного ученого, поэтому она приложила весь свой интеллектуальный талант для получения им профессорского звания.

Альберта не выгнали из Бюро только потому, что отец Марселя Гроссмана, директор крупного завода по выпуску сельхозтехники, долгое время проработал с Фридрихом Галлером, директором Патентного бюро. В благодарность за дружбу он терпел этого несносного, хвастливого бездельника. Чтобы понять, из какого человеческого материала Милеве пришлось вылепливать всемирно известного ученого, нужно хорошенько представлять себе, кем был на тот момент ее ненаглядный.

Конрад Габихт, Морис Соловин и Альберт Эйнштейн.

Альберт никогда не работал самостоятельно, для обкатки своих сумасбродных идей ему всегда нужна была компания. Первым его компаньоном «по делам науки», если так можно выразиться, стал Мишель Анжела Бессо, с которым он познакомился на втором курсе учебы в Политехникуме и затем работал в Патентном бюро, где, кстати, его ценили несколько выше, чем его друга (он был зачислен в штат без испытательного срока и быстро получил 1-й разряд). Вместе они каратали вечера и воскресные дни. Лекции и практические занятия Альберт безбожно пропускал, так что для сдачи экзаменов ему понадобился еще один товарищ, Марсель Гроссман, лекции которого сегодня находятся в музее Политехникума как образцовые. Гроссман и Марич придавали всему, к чему прикасался тогда Эйнштейн, академическую респектабельность; детскую непосредственность и юношескую смелость дарили ему Бессо и еще два легкомысленных типа — Конрад Габихт и Морис Соловин, которые входили в учрежденную Альбертом после свадьбы с Милевой «Академию Олимпия» — кружок для болтунов ни на минуту не смолкающих.

Фридрих Галлер, Мишель Бессо, Конрад и Пауль Габихты.

В свободное от службы время Альберт просиживал с ними за кружкой пива в дешевых забегаловках. Иногда они всей гурьбой ходили в театр или на концерты. К слову сказать, музыка сопровождала Эйнштейна всю жизнь. Его мать была прекрасной пианисткой; она отдала сына учиться на скрипке. Со временем он втянулся в мир музыки, окружил себя музыкантами и сам любил устраивать концерты прямо у себя дома или в гостях. Милева же не любила эти шумные сборища, сидела с сыном дома и трудилась над научными статьями Альберта. В то время усадить мужа за письменный стол было нереально; некоторую настойчивость он проявлял на репетициях концертов и при разучивании новых музыкальных партий на скрипке — на большее его терпения не хватало.

Его трудности с математикой

Прежде чем мы приступим к анализу научных статей Милевы, нужно как следует усвоить одну простую вещь. Альберт никогда не мыслил уравнениями и формулами, он не умел делать длинные, многостраничные выкладки, которые мы находим в начале третьего тома его (?) «Собрания научных трудов» [1], где помещены теоретические работы периода их пылкой любви. Всю жизнь он нуждался в помощниках-математиках, которые выполняли для него все вычисления. У нас нет ни одного листка бумаги того периода, где бы его рукой были написаны формулы статистической физики, пробные выводы или иные свидетельства, которые говорили бы нам о его работе как математика. Черновики и оригинальные рукописи статей того периода бесследно исчезли. Зато имеется масса свидетельств, доказывающих его некомпетентность в математических вопросах. Об этом он сам откровенно писал в двух своих автобиографиях.

В «Автобиографических заметках» 1949 года он писал, что в 12 – 16 лет познакомился с элементарной геометрией, основами дифференциально-интегрального исчисления и

«главными результатами и методами естественных наук по очень хорошему популярному изданию, в котором изложение почти везде ограничивалось качественной стороной вопроса (бернштейновские естественнонаучные книги для народа — труд в 5-6 томов); книги эти я читал, не переводя дыхания. К тому времени, когда я в возрасте 17 лет поступил в Цюрихский политехникум в качестве студента по физике и математике, я уже был немного знаком и с теоретической физикой.

Там у меня были прекрасные преподаватели (например, Гурвиц, Мин-ковский), так что, собственно говоря, я мог бы получить солидное математическое образование. Я же большую часть времени работал в физической лаборатории, увлеченный непосредственным соприкосновением с опытом. Остальное время я использовал главным образом для того, чтобы дома изучать труды Кирхгофа, Гельмгольца, Герца и т. д. Причиной того, что я до некоторой степени пренебрегал математикой, было не только преобладание естественнонаучных интересов над интересами математическими, но и следующее своеобразное чувство. Я видел, что математика делится на множество специальных областей и каждая из них может занять всю отпущенную нам короткую жизнь. И я увидел себя в положении буриданова осла, который не может решить, какую же ему взять охапку сена. Дело было, очевидно, в том, что моя интуиция в области математики была недостаточно сильна, чтобы уверенно отличить основное и важное от остальной учености, без которой еще можно обойтись. Кроме того, и интерес к исследованию природы, несомненно, был сильнее; мне как студенту не было еще ясно, что доступ к более глубоким принципиальным проблемам в физике требует тончайших математических методов. Это стало мне выясняться лишь постепенно, после многих лет самостоятельной научной работы» [1, т. 4, с. 263 – 264].

Итак, в доме Альберта находилась популярная энциклопедия по естествознанию, которую он к 17 годам с некоторым любопытством пролистал. Но давайте подумаем, если юноша удовлетворяется только «качественная сторона вопроса», получится ли из него в будущем хороший исследователь? Из письма к Милевы мы знаем, что «труды Кирхгофа, Гельмгольца, Герца и т. д.» он изучал только для того, чтобы не выглядеть в ее глазах круглым идиотом. Из других источников нам также известно, что в физической лаборатории он больше баловался, чем добросовестно работал. Лично знавший его Карл Зелиг писал:

«Доктор Иозеф Заутер, который был главным ассистентом Вебера, рассказал мне, что в бытность свою студентом Эйнштейн, работая в лаборатории профессора физики Жана Перне, серьезно поранил себе руку в июне 1899 года во время взрыва... В начале того же года Перне, рассерженный тем, что Эйнштейн стал отлынивать от практических занятий в физической лаборатории, написал в ректорат докладную записку с просьбой объявить Эйнштейну выговор, что и было сделано. Об этом рассказал в 1943 году профессор Франк Танк...» [5, с. 206].

За весь зимний семестр 1898/99 гг. по лабораторному практикуму у Перне Альберт получил неудовлетворительную оценку. В отношении математики дела обстояли еще хуже: в молодости он ею вообще не интересовался, в связи с чем позднее у него развился комплекс неполноценности. Из приведенного отрывка мы видим, как он ищет и не находит для себя оправданье. В «Автобиографических набросках» 1955 года мы читаем примерно то же самое:

«1896 – 1900 гг. — обучение на отделении преподавателей специальных дисциплин швейцарского политехникума. Вскоре я заметил, что довольствуюсь ролью посредственного студента. Для того чтобы быть хорошим студентом, нужно обладать легкостью восприятия; готовностью сконцентрировать свои силы на всем том, что читается на лекции; любовью к порядку, чтобы записывать и затем добросовестно обрабатывать преподносимое на лекциях. Всех этих качеств мне основательно недоставало, как я с сожалением установил. Так постепенно я научился ладить с не совсем чистой совестью и организовывать свое ученье так, как это соответствовало моему интеллектуальному желудку и моим интересам.

Некоторые лекции я слушал с большим интересом. Но обыкновенно я много "прогуливал" и со священным рвением штудировал дома корифеев теоретической физики. Само по себе это было хорошо и служило также тому, что нечистая совесть так действенно успокоилась, что душевное равновесие не нарушалось сколько-нибудь заметно. Это широкое самостоятельное обучение было простым продолжением более ранней привычки; в нем принимала участие сербская студентка Милева Марич, которая позднее стала моей женой.

Однако в физической лаборатории профессора Г. Ф. Вебера я работал с рвением и страстью. Захватывали меня также лекции профессора Гейзера по дифференциальной геометрии, которые были настоящими шедеврами педагогического искусства и очень помогли мне позднее в борьбе, развернувшейся вокруг общей теории относительности. Но высшая математика еще мало интересовала меня в студенческие годы. Мне ошибочно казалось, что это настолько разветвленная область, что можно легко растратить всю свою энергию в далекой провинции. К тому же по своей наивности я считал, что для физики достаточно твердо усвоить элементарные математические понятия и иметь их готовыми для применения, а остальное состоит в бесполезных для физики тонкостях,— заблуждение, которое только позднее я с сожалением осознал. У меня, очевидно, не хватало математических способностей, чтобы отличить центральное и фундаментальное от периферийного и не принципиально важного.

В эти студенческие годы развилась настоящая дружба с товарищем по учебе, Марселем Гроссманом. Раз в неделю мы торжественно шли с ним в кафе «Метрополь» на набережной Лиммат и разговаривали не только об учебе, но и, сверх того, обо всех вещах, которые могут интересовать молодых людей с открытыми глазами. Он не был таким бродягой и чудаком, как я, но был связан со швейцарской средой и в пределах возможного не потерял внутренней самостоятельности.

Кроме того, он обладал в избытке как раз теми данными, которых мне не хватало: быстрым восприятием и порядком во всех отношениях. Он не только посещал все лекции, которые мы считали важными, но и обрабатывал их так замечательно, что если бы его тетради перепечатать, то их вполне можно было бы издать. Для подготовки к экзаменам он одалживал мне эти тетради, которые служили для меня спасательным кругом; о том, как мне жилось бы без них, лучше не гадать». [1, т. 4, с. 351 – 352].

Перед нами ничем непримечательная личность, которая к тому же ехидно подсмеивается над нами с вами, дорогой читатель. Фраза «в физической лаборатории профессора Г. Ф. Вебера я работал с рвением и страстью» звучит прямо-таки издевательски. Автор надеется, что читатель никогда не узнает правды о конфликте его с Переном, ассистентом декана Г. Ф. Вебера. Всё, о чём он пишет, явно недостаточно для написания математических работ, которые появились уже в конце 1900 года. Эйнштейн рассказывает о помощнике по математике Гроссмане, но с ним он начал сотрудничать в связи с разработкой ОТО. В таком случае, кто сделал сложнейшие вычисления для статей по термодинамике и статистической физике, помещенных в третьем томе "Собрания научных трудов"?

Больцмана не читал, но с ним не согласен

Тут же перед нашим взором всплывет образ Милевы Марич — тихой, незаметной мышки, стесняющейся появиться на людях. Ее биографы в один голос твердят о ее блестящих математических способностях. Она легко разобралась в сложной молекулярно-кинетической теории Больцмана, учась в Политехникуме. Еще до замужества влюбленная по уши девушка начала писать докторскую диссертацию для своего будущего мужа. Диссертация выкристаллизовалась из нескольких ее статей, которые посылались в «Annalen der Physik». Назовем первый десяток ее, фактически, единолично написанных работ (нумерация соответствует перечню статей третьего тома [1]):

1. Следствия из явления капиллярности (1901).
2. О термодинамической теории разности потенциалов… (1902).
3. Кинетическая теория теплового равновесия и второго начала термодинамики (1902).
4. Теория основ термодинамики (1903).
5. К общей молекулярной теории теплоты» (1904).
6. Новое определение размеров молекул» (1905).
7. Об одной эвристической точке зрения, касающейся возникновения и превращения света (1905).
8. О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты (1905).
9. К теории броуновского движения (1906).
10. К теории возникновения и поглощения света (1906).

Милева Марич в возрасте 21 года (1896), когда она
отправилась из своего дома в Новом Саду учиться в Цюрих.

Статья, о которой говорил Борн в своем выступлении 1955 года [2] и за котору Эйнштейн в 1922 году получил Нобелевскую премию, стоит в этом списке под номером 7. Как утверждал Борн, она действительно тесно примыкает к предыдущим и последующим статьям. За двумя вводными параграфами этой статьи:

1) Об одной трудности в теории излучения черного тела;
2) О планковском определении элементарных квантов;

идут четыре параграфа, над которыми витает математический дух Больцмана. Милева жила и наслаждалась им, но его абсолютно не улавливал Альберт. Эти четыре параграфа имели следующие названия:

3) Об энтропии излучения;
4) Предельный закон для энтропии монохроматического излучения при малой плотности излучения;
5) Исследование зависимости энтропии газов и разбавленных растворов от объема в молекулярной теории;
6) Интерпретация выражений для зависимости энтропии монохроматического излучения от объема, полученной на основе принципа Больцмана.

Все четыре параграфа пронизаны единой математической идеей и представляют собой одно логическое целое. Кто знаком с этой манерой творчества по предыдущим статьям, тот не станет отрицать принадлежность данного стиля изложения одному и тому же автору, глубоко знающему статистическую теорию энтропии Больцмана. В последующих после преамбулы параграфах Милева Марич передает ход своих мыслей и опытные данные, натолкнувшие ее на эту, как она сказала своим заголовком статьи, «эвристическую точку зрения». Шестой параграф венчает вопрос, логично возникающий из всего представленного ею анализа:

«Монохроматическое излучение малой плотности (в пределах области применимости закона излучения Вина) в смысле теории теплоты ведет себя так, будто оно состоит из независимых друг от друга квантов энергии величиной Rβυ/N …

Но если монохроматическое излучение (достаточно малой плотности) в смысле зависимости энтропии от объема ведет себя как дискретная среда, состоящая из квантов энергии величиной Rβυ/N, то напрашивается вопрос, не являются ли законы возникновения и превращения света такими, как если бы свет состоял из подобных же квантов энергии?» [1, т. 3, с. 102].

Как видим, квант энергии hυ здесь выглядит несколько непривычно для нас. Мы привыкли писать формулу Планка для энергии излучения абсолютно черного тела как

Она же писала в своей статье формулу Планка для плотности энергии через постоянные α и β:

Постоянную Больцмана она выражала через отношение универсальной газовой постоянной (R) к числу Авогадро (N). Поэтому в окончательной «формуле Эйнштейна» для фотоэффекта (правильнее сказать, конечно, в «формуле Марич») не фигурирует постоянная Планка (h = βR/N):

,

где P — работа выхода для электронов проводимости. Параметр β = 1/kT, фигурирующий в этой формуле, заменяет температуру; эта удобная форма выражения для энергии, отнесенной к одному осциллятору: U = 1/β (подробнее, см. [2, с. 123] или Борн против Эйнштейна).

Поставив ребром указанный выше вопрос, Милева Марич обратилась к экспериментам Филиппа Ленарда, лекции которого слушала в Гейдельбергском университете, куда сбежала из Политехникума. Она была в восторге от лекций «замечательного профессора Ленарда», который рассказывал о поражающей ее воображение скорости молекул газа (400 м/с) и малости пути их свободного пробега (сотая доля толщины волоса). Об этом Милева с восторгом писала Альберту сразу же по прибытии в Гейдельберг в октябре 1897 года (см. Милева Марич как подруга и жена Эйнштейна). Поэтому вполне естественно, что в своей работе 1905 года о квантах света она ссылается на работы своего учителя, опубликованные в 1902 и 1903 гг. в том же журнале, в котором печаталась сама, т.е. в «Annalen der Physik».

Свадебная, 1903 год.

Кому здесь не понятно, что квантовая теория излучения и поглощения выросла непосредственно из дискретной теории Больцмана, которой Милева отдала последние годы? Однако давайте, дорогой читатель, откроем том 3 на странице 44 четырехтомника «Собрания научных трудов» Эйнштейна, где излагается статья 3 «Кинетическая теория теплового равновесия и второго начала термодинамики», и начнем читать параграф 6, имеющий заголовок «О механическом смысле величины h» (не следует путать эту h с постоянной Планка). Тут же, к заголовку, автор дает сноску: «Ср. L. Во1tzmann. Gastheorie. Т. II, §§ 33, 34, 42», т.е. он просит читателя сравнить свои модельные построения с соответствующим местом в лекции Больцмана. Далее следует сугубо математический текст:

Кинетическая энергия L системы является однородной квадратичной функцией величин q. Линейной подстановкой всегда можно ввести переменные r такие, что кинетическая энергия примет вид:

и что

если интегралы распространить на соответствующие бесконечно малые области. Величины r Больцман называет моментоидами. Средняя кинетическая энергия, соответствующая моментоиду, если система объединяется в одно целое с другой системой, обладающей много большей энергией, принимает вид:

Таким образом, средняя кинетическая энергия всех моментоидов системы одна и та же и равна

где L — кинетическая энергия системы. [1, т. 3, с. 44].

Пожалуй, этого отрывка будет достаточно, чтобы сравнить его с любопытным пассажем из «Автобиографических заметок» 1949 года. Полюбуйтесь, что писал Эйнштейн о молекулярно-кинетической теории и своем новом подходе к энтропии, которая является гвоздем статистической модели Больцмана. Сказав несколько слов о достижениях Планка, он решил было рассказать,

«к каким следствиям ведет этот закон теплового излучения как для фотоэлектрического эффекта и других родственных ему явлений, связанных с превращениями лучистой энергии, так и для теплоемкости тел, в частности твердых тел. Но все мои попытки приспособить теоретические основы физики к этим результатам потерпели полную неудачу. Это было так, точно из-под ног ушла земля и нигде не было видно твердой почвы, на которой можно было бы строить…

Мои личные интересы в эти годы были направлены не столько на отдельные следствия из результатов Планка, как бы важны они ни были; главным моим вопросом был следующий. Какие общие выводы позволяет сделать формула излучения относительно структуре излучения и вообще относительно электромагнитной основы физики? Прежде чем говорить об этом подробнее, я должен коротко упомянуть о некоторых исследованиях, относящихся к броуновскому движению и родственным ему предметам (явления флуктуации) и основанных главным образом на классической кинетической теории.

Не будучи знакомым с появившимися ранее исследованиями Больцмана и Гиббса, которые по существу исчерпывают вопрос, я развил статистическую механику и основанную на ней молекулярно-кинетическую теорию термодинамики». [1, т. 4, с. 275].

Стоп! Здесь Эйнштейн недвусмысленно заявил, что теорию Больцмана он не знает. Но ведь автор процитированной статьи «Кинетическая теория теплового равновесия и второго начала термодинамики», появившейся до статей по броуновскому движению, не только сослался на главный труд Больцмана, использовал его своеобразный термин «моментоид», но и вывел отличным от больцмановского способа формулу энтропии. Между тем, процитированное здесь предложение — единственное место из двух автобиографий, где Эйнштейн хоть что-то сказал, чему были посвящены три якобы им написанные статьи с длиннющими математическими выкладками.

Вслед за этой небрежно брошенной в последнем абзаце фразой появились сотни его героических жизнеописаний, где сказанное им представало, например, в таком виде:

«В то время ему не было известно, что, за исключением некоторых новых частностей, он, в сущности, повторял исследования Больцмана. Почти одновременно с Эйнштейном в какой-то мере теми же проблемами занимался американский ученый Уиллард Гиббс. Это свидетельствует о том, сколь многого достиг к тому времени Эйнштейн — почти самоучка, ведь Больцман и Гиббс — гиганты науки. Более того, разработав статистические принципы, для которых впоследствии ему удалось найти более широкое применение, Эйнштейн уже тогда значительно превзошел достижения этих ученых» [3, с. 36]

Заметим, между прочим, последний пассаж взят из книги, написанной помощником Эйнштейна по математике, Бенешем Хофманом, и личным секретарем Эйнштейна, Элен Дюкас. Кому еще можно верить, если не им? Хотя до нас дошли два письма Гроссмана за 1901 год (см. Эпистолярное наследие Эйнштейна периода 1895 – 1920 гг.), в одном из которых он сообщает об изучении работ Больцмана. В самом деле, отношение между Милевой и Альбертом в то время развивались более или менее гармонично, они вместе изучали физику и он мог попытаться вникнуть в кинетическую теорию газов, в которой она разбиралась намного лучше его.

Альберт: некогда мне заниматься физикой

Когда человек искажает события своей жизни, он часто попадает впросак. Так, например, фальсифицируя историю возникновения психоанализа, Фрейд в предисловии ко второму изданию книги «Исследование истерии» (1-е изд. 1895 г., 2-е изд. 1908 г.) написал, что о сексуальной основе истерии он задумался в самом начале своей врачебной практики. Однако в четвертой главе указанной книги есть места, где он утверждает прямо противоположное: «...я и помыслить не мог о том, что сексуальный невроз может служить основой для истерии». Подобных оговорок, свидетельствующих об обмане общественности, отец-основатель психоанализа наделал масса (см. Как возник психоанализ).

Точно такие же разоблачительные оговорки мы наблюдаем у отца-основателя релятивизма. Наиболее яркими являются оговорки, касающиеся эксперимента Майкельсона — Морди. Сначала он утверждал, что о данном эксперименте он не только знал, но и пытался его поставить во время учебы в Политехникуме. Но незадолго до своей кончины он дал несколько интервью, в которых говорил о своем полном неведении относительно этого знаменитого опыта (см. Эксперимент Майкельсона – Морли). Теперь кто может серьезно поверить его словам: «я развил статистическую механику и основанную на ней молекулярно-кинетическую теорию термодинамики» независимо ни от кого, добавим мы, полностью самостоятельно, не читая труды всеми признанных классиков?

Верно, что четвертая статья названа Милевой Марич несколько претенциозно — «Теория основ термодинамики». Но думать, что развитая в ней теория не опиралась на разработки Максвелла и Больцмана — значит, проявить крайнюю наивность в физических вопросах, которую могут демонстрировать легкомысленные журналисты, но не серьезные исследователи. И когда бы Эйнштейн успел развить свою теорию? Может быть, когда он в растрепанных чувствах подыскивал себе работу, испытывая, как он сам писал, «интеллектуальную депрессию после благополучного окончания учебы» [1, т. 4, с. 352]?

Давайте бегло проследим за Хронологией жизни Эйнштейна в период с момента получения Альбертом диплома до момента выхода третьей статьи, предположительно написанной Милевой. После окончания Политехникума он проводит время (с 27 июля по 9 августа 1900 г.) с матерью, сестрой и тетей. Потом едет в Цюрих к профессору математики Адольфу Гурвицу, который отказывается взять его к себе в ассистенты. 18 августа он едет к отцу в Милан, начало сентября проводит в Венеции, с 21 сентября беззаботно путешествует по Lago Maggiore, а 7 октября возвращается в Цюрих. Чем он занимался там зимой 1900/1901 гг., нам неизвестно, но 13 декабря он отослал в «Annalen der Physik» свою первую статью «Следствия из явления капиллярности», которая была опубликована 1 марта 1901 года.

Ее содержание мы разберем позже, а пока заметим лишь, что писала Милева в связи с этой статьей своей подруге Элен Савич в письме от 20 декабря 1900 года: «Альберт написал статью по физике, которая в скором времени будет опубликована, наверное, в "Annalen der Physik". Можешь себе представлять, как я горда за моего возлюбленного. Это ведь работа не одного дня, а очень продолжительная; она касается теории жидкости. Мы послали ее частным образом также Больцману» [6, Doc. 85].

Местоимение «мы», часто используемое Милевой, говорит о ее непосредственном участии в делах своего сначала друга, а потом и мужа. В процитированном отрывке она, похоже, хочет недвусмысленно указать на то, что первую работу написал один Альберт. Однако сам Альберт в письме, посланном Милеве из Винтертура (Winterthur), имея в виду всё ту же первую статью, написал так: «Здешний профессор Вебер интересуется моими работами. Я дал ему нашу статью. Только бы поскорее мы получили счастливую возможность двигаться и далее вместе этой прекрасной дорогой [совместного творчества]» [6, Doc. 107]. Об исключительной скромности Милевы, ее полной самоотдаче ради успешной научной карьеры Альберта читайте в разделе Эйнштейн в детские и молодые годы.

23 Марта Альберт снова едет в Милан к родителям. Отсюда он и его отец пишут письма Оствальду в Лейпциг и Камерлингу-Оннесу в Лейден о предоставлении ассистентской должности. Оба знаменитых профессора оставили их письма без ответа. В начале мая Альберт договаривается о временной работе в Техникуме в Винтертуре (Technical School in Winterthur), где он будет подменять с 16 мая по 11 июля местного учителя. Но до этого он успел встретиться с Милевой на озере Комо, где они зачали Лизерль.

В начале июля Альберт пытался устроиться в техникум в Бугдорфе (Burgdorf), в конце этого же месяца — в среднюю школу в Фраунфилде (Frauenfeld); в обоих случаях безуспешно. В сентябре ему всё-таки удастся получить временную работу учителя в школе-интернате в Шафхаузене (Schaffhausen). Но весь летний период он отдыхал с матерью на курорте в Меттменштеттене (Mettmenstetten), вдали от Милевы.

После зачатия первого ребенка он старательно избегает ее. Следующая короткая встреча с ней происходит только в начале ноября, после чего беременная Милева уезжает к себе на родину, в Новый Сад. В январе 1902 года она родила Лизерль. В это время, начиная с празднования Рождества, Альберт находится вместе с матерью и сестрой на курорте Mettmenstetten, где знакомится с Анной Майер-Шмид (Meyer-Schmid), тогда просто Шмид (об этой и других любовных историях читайте в разделе Любовницы Эйнштейна).

Приехав с курорта в Mettmenstetten, мать собирает сына для поездки в Берн. 11 февраля 1902 года он приезжает в этот швейцарский город и останавливается в доме Анны Сиверс (Anna Sievers). 30 апреля редакция «Annalen der Physik» получает вторую статью под длинным названием «О термодинамической теории разности потенциалов между металлами и полностью диссоциированными растворами их солей и об электрическом методе исследования молекулярных сил». Об этой второй статье, как и о первой, мы подробно поговорим ниже, но уже сейчас следует сказать, что обе они были написаны, скорее всего, по замыслу Эйнштейна. Марич, видимо, принимала какое-то участие, но оно было минимальным. Это отразилось и на их содержании, заметно отличающемся от содержания трех последующих статей.

Весной 1902 года в местной газете появилось объявление: «Частные уроки по математике и физике для студентов и учащихся весьма добросовестно дает Альберт Эйнштейн, обладающий дипломом федерального Политехникума». Единственным, кто клюнул на это объявление, был «бедный румынский еврей» Морис Соловин, тут же сделавшийся самым близким и преданным другом Альберта. Первое время друзья сидели дома, гуляли по улице, вместе обедали, при этом непрерывно болтали обо всем на свете. Деньги Соловин по своей бедности не платил, но Эйнштейн и не требовал их от него, так как то, чем они занимались, вряд ли можно было назвать «уроками по математике и физике». Эйнштейн нашел свободные уши, готовые слушать его целыми днями. Этому он был несказанно рад и ничего больше не требовал от обладателя этих ушей (Об этом беспечном времени препровождения рассказывается в разделе Эйнштейн в детские и молодые годы).

С 16 июня 1902 года Альберт получает обещанное ему еще в декабре прошлого года место в Швейцарском Патентном Бюро (Swiss Patent Office), а через неделю, 23 июня, он выходит на работу в качестве третьеразрядного клерка этой конторы, в которой проработает семь лет и четыре месяца. Через три дня в редакцию «Annalen der Physik» приходит третья статья «Кинетическая теория теплового равновесия и второго начала термодинамики» по стилю сильно отличающаяся от предыдущих двух. Ее можно было бы охарактеризовать такими эпитетами как добротная, глубокая, цельная. Автор ее преследовал исключительно теоретические цели, причем затрагивающие фундамент термодинамики. В основе же двух предыдущих статей лежала плохо продуманная идея полуэмпирического характера, которая не имела никакого продолжения. Таким образом, если первые две статьи следует назвать любительскими или даже дилетантскими, то последующие три — мастерскими или профессиональными. Рассмотрим их подробно.

Первая статья Эйнштейна — Марич

Автор (или авторы, хотя главным ответственным лицом здесь был всё-таки Эйнштейн) статьи № 1, «руководствуясь аналогией с гравитационными силами», предположил, что «относительная потенциальная энергия взаимодействия двух молекул имеет вид

P = P_∞ – c₁c₂φ(r),

где c_α — характеристические постоянные для двух рассматриваемых молекул, а φ(r) — независимая от природы молекул функция расстояния между ними» [1, т. 3, с. 10].

Произведя соответствующие математические манипуляции и сопоставив ряд эмпирических данных, взятых из учебника В. Оствальда по общей химии, автор заключил, что действительно «каждому атому соответствует молекулярное поле притяжения, не зависящее от температуры и от способа, которым этот атом связывается химически с другими атомами». При этом «введение функции φ(r), не зависящей от природы молекул, следует понимать как некое приближение».

Автор также подметил следующую закономерность: «с возрастанием атомного веса постоянные c_α в общем увеличиваются, хотя не всегда и не пропорционально»; и добавил: «наша теория, по-видимому, не оправдывается для веществ с малым атомным объемом». Кроме того, он сделал любопытное примечание, свидетельствующее о его интересе к фундаментальным проблемам физики. Он написал: «Вопрос о том, нет ли какой-либо связи между нашими [т.е. молекулярными] силами и силами гравитации, должен оставаться пока совершенно открытым» [1, т. 3, с. 17].

Эти выводы были сделаны на основе сравнения расчетных характеристических постоянных c_α с эмпирическими. В частности, для водорода, углерода и кислорода путем подгоночных вычислений найдено:

c_H = –1,6,     c_C = 55,0,     c_O = 46,8.

Отсюда для лимонного терпена (химическая формула C₁₀H₁₆) расчетный совокупный коэффициент Σc_α равен: 10 × 55 – 16 × 1,6 = 524; между тем как опыт дал величину 510. Муравьиная кислота (CO₂H₂) имеет расчетный совокупный коэффициент: 55 + 46,8 × 2 – 2 × 1,6 = 145, эмпирический — 140. Сравнение производилось для 17 химических соединений, куда входили три названных элемента.

Далее автор нашел характеристические постоянные c_α для Cl, Br и J:

c_Cl = 60,     c_Br = 150,     c_J 198

и составил таблицу еще для 24-х соединений с расчетными и опытными данными. Например, для хлортолуола (C₇H₇Cl) расчетный коэффициент получился равным 434, эмпирический — 438; для бромбензола (C₆H₅Br) эти значения соответственно равны 474 и 411. После этой таблицы автор подмечает: «Мне кажется, что отклонения от нашей теории больше для тех веществ, которые обладают сравнительно большим молекулярным весом и малым молекулярным объемом» [1, т. 3, с. 13]. Хотя хлортолуол, а также хлористый бензилиден (соответствующие числа 495 и 492), явно опровергают этот вывод.

В следующей таблице были приведены отношения, составленные из особо подсчитанной теплоты испарения и всё того же совокупного характеристического коэффициента Σc_α. Подозрительным в ней является то, что автор рассчитал менее половины заявленных в таблице соединений, насчитывающей 33 наименования, причем ранее им не рассматриваемых. У читателя создается впечатление, будто автор специально выбрал для себя только те соединения, для которых величина искомого отношение равна примерно 2,51, хотя в таблице фигурируют, с одной стороны, такие значения, как 2.30 и 2.36, с другой — 2.78 и 2.89.

Пусть эти отношения «довольно явственно зависят от состава вещества», пишет автор, «содержащийся в таблице материал всё же можно использовать для того, чтобы определить, хотя бы по порядку величины, то число, на которое необходимо умножить наши значения c_α, чтобы выразить их в выбранных нами абсолютных единицах. Для искомого множителя в среднем получается следующее значение: 1.62 × 10⁴ » [1, т. 3, с. 15]. В конце статьи приводится еще один способ нахождения этого множителя, посчитанный для восьми уже совершенно новых веществ. Здесь порядок величины остается прежним (10⁴), различие же касается множителя, который колеблется от 1.7 до 2.00.

После прочтения первой статьи у читателя складывается устойчивое мнение в недобросовестности автора. Мы видим, как он неприкрыто занимается числовой подгонкой. Мало того, что найденные им величины в рамках каждой таблицы приводятся без всякой оценки погрешности измерения и гуляют в широких пределах, все приведенные им таблицы содержат различные группы веществ, так что в их специальном подборе можно не сомневаться. Нахождение пересчетного множителя, переводящего относительные характеристические константы c_α в абсолютные, должен дать невообразимо большой числовой разброс. Приходиться только удивляться, как автор не чувствует этого.

Однако чудовищная манера работы с числовыми массивами поражает и возмущает намного меньше, чем абсурдность главной идеи, лежащей в основе статьи. Разумеется, сила сцепления атомов в молекулах вещества зависит от температуры, структуры и состава химического соединения. Искать здесь некие универсальные постоянные молекулярного сцепления, пригодные для всех химических соединений, — затея совершенно ошибочная. Как можно было публиковать такую статью?! Кто ее пропустил?! Куда смотрели Планк и Вин?! Странно, очень странно... Не удивительно, что автор так перенапрягся, когда искал свою мифическую универсальную отмычку для молекулярной физики.

Кажется, дальше падать некуда, автор достиг уже дна. Но нет, на всеобщее обозрение он представил еще и некую теорию. Не забывайте, статья названа «Следствия из явления капиллярности». Спросите: причем здесь капиллярность? А вот причем. Статья начинается с мысленного эксперимента, характерного для «парадоксального» образа мыслей Эйнштейна (можно не сомневаться, что его придумал он, так как с подобными «экспериментами» мы сталкиваемся и в других местах). Процитируем первую страницу его первой статьи, которая навеяна, несомненно, определенными разделами капиллярной теории, связанными с поверхностными натяжениями жидкости:

«Если обозначить через γ механическую работу, которую необходимо совершить над жидкостью, чтобы увеличить ее поверхность на единицу, то γ не будет полным приращением энергии системы, в чем можно убедиться, рассматривая следующий круговой процесс. Возьмем некоторое количество жидкости, обладающее температурой T₁ (абсолютной) и поверхностью O₁. Увеличим теперь изотермически поверхность от O₁ до O₂ [интересно, каким это образом?], после чего повысим температуру до T₂ (при постоянной поверхности), а затем уменьшим поверхность [как это можно сделать?] до O₁ и охладим жидкость снова до T₁. Если теперь предположить, что к телу нельзя подвести большее количество тепла, чем допускается его теплоемкостью, то при круговом процессе суммарное количество тепла, подведенное к телу, будет равно суммарному количеству тепла, отнятому от тела. Таким образом, в соответствии с законом сохранения энергии суммарная механическая работа, совершенная над телом, также будет равна нулю.

Итак, должно выполняться уравнение

(O₂ – O₁)γ₁ – (O₂ – O₁)γ₂ = 0     или     γ₁ = γ₂.

Однако это противоречит опыту [какому?].

Таким образом, остается только предположить, что изменение поверхности сопровождается также обменом тепла и что поверхности соответствует своя особая удельная теплоемкость. Обозначая через U энергию, через S — энтропию единицы поверхности жидкости, через s — удельную теплоемкость поверхности, через w₀ — количество тепла в механических единицах, необходимое для образования единицы поверхности, находим...» [1, т. 3, с. 7].

Далее записываются дифференциалы для U и S, которые, однако, никакого отношение к процитированному мысленному эксперименту и выписанной здесь формуле отношения не имеют. Более того, нет ничего общего между содержанием первого абзаца и выписанной здесь тавтологией. В самом деле, в тексте фигурируют две температуры T₁ и T₂, в формуле они отсутствуют. Равенство двух механических работ по растяжению и сжатию поверхности (γ₁ = γ₂), вытекающее якобы из математического выражения, абсурдно в силу бессмысленности самого тождества. По условию эксперимента фигурирует лишь одна механическая работа γ.

Эйнштейна изображают ребенком как на этой фотографии. Это в определенном смысле верно. Однако здесь скульптор вылепил тетрадь, в которой выписаны формула E = mc² и формула для квантового фотоэффекта. Не Эйнштейном выведены эти формулы; правильнее было бы туда вписать формулу (O₂ – O₁)γ₁ – (O₂ – O₁)γ₂ = 0, как наиболее адекватно характеризующую его способности к математическому моделированию физических ситуаций.

Из процитированного выше текста чувствуется, что автор много времени потратил на числовую подгонку, пытаясь реализовать свою утопическую идею по розыску универсальной молекулярной силы сцепления атомов в молекулах, не зависящей от их сорта и температуры нагрева. Затем у него появилась естественная мысль, связать полученный числовой массив, с некой теорией. Он использовал этот свой мысленный эксперимент в качестве дымовой завесы и записал первую формулу. Она должна была создать у читателя впечатление о некой связи его числовой подгонки с капиллярной теорией, реально же никакой смысловой нагрузки первое уравнение не несет.

Далее Альберт обратился к Милеве примерно со следующими словами: «Послушай, Дорогая, набросай-ка мне странички две каких-нибудь формул из термодинамики, чтобы они перебросили логический мостик к моему числовому массиву. Я тут уже придумал некую мысленную ситуацию, взятую из капиллярной теории. Может быть, к этому добавить что-нибудь, связанное с энтропией? Ты ведь интересуешься этими делами». Бедной девушке деваться некуда: она выписала с десяток уравнений, создающих видимость теории. Эйнштейн морочил всем голову. Понятно, что никакими средствами, в том числе через термодинамические законы, невозможно доказать существование каких-то универсальных констант c_α. Тем не менее, сверстанную таким образом статью № 1 в середине декабря 1900 года Альберт отослал в редакцию журнала «Annalen der Physik». О, чудо, через пару месяцев журнал напечатал ее.

Почему мы так подробно остановились на этой первой статье Эйнштейна? Дело в том, что она самым наглядным образом демонстрирует нам образ его мыслей и стиль работы. С зимы 1901 года до лета 1905 года времени прошло немного. Отдыхая на курорте Меттменштеттене, играя на скрипке и флиртуя с симпатичными девушками, Альберт не приобрел исследовательского опыта физика-теоретика. Он остался таким же шалопаем и бездельником, каким был в Политехникуме, поднаторевшим только в одном — в интеллектуальной эксплуатации несчастной Милевы, которая не могла надышаться на своего симпатичного и озорного возлюбленного.

Мы узнаем его путаный, местами просто издевательский стиль в «Кинематической части» статьи 1905 года «К электродинамике движущихся тел», в которой «Электродинамическая часть» написана Милевой Марич. В написании промежуточных статей по общей теории относительности принимал активное участие Марсель Гроссман, а главное математическое решение финишной статьи было подсказано Давидом Гильбертом. При этом обеим теориям относительности тоже предшествовали некие утопические и во много ошибочные идеи, которые затем присоединялись локомотивом к чужеродному математическому поезду. Верхогляды, легко усваивая содержание утопических идей, дивились и восхищались ими, думая, что они явились плодом строгих математических исследований. На самом деле, сложные математические выкладки выполняли в статьях Эйнштейна второстепенную функцию картофельного гарнира, который подавался после его жирной идеи-котлеты.

Вторая статья Эйнштейна — Марич

В написании второй статьи «О термодинамической теории разности потенциалов между металлами и полностью диссоциированными растворами их солей и об электрическом методе исследования молекулярных сил» Марич принимала более активное участие, чем в написании статьи о «Следствиях из явления капиллярности». Название первого параграфа, «Гипотетическое обобщение второго начала механической теории тепла», об этом свидетельствует. Ее теоретический интерес ко второму началу термодинамики был долгим и устойчивым. Интерес же Эйнштейна в первые годы после окончания Политехникума носил больше практический характер, чем теоретический. Это связано было с присущими для его ума устремлениями, которые сформировались еще в детстве. Ребенком он часто бывал в электромеханической мастерской его дяди и отца, где видел, как они бились над узкотехническими задачами, связанными с конструированием электрических машин. До конца своих дней он воспринимал себя инженером-новатором, лихо справляющимся с решением сложных технических задач.

Тенденция к изобретательству особенно отчетливо проступает у него тогда, когда, кажется, он достиг пика славы как самый успешный физик-теоретик. В период с 1926 по 1933 год он тесно сотрудничал с Лео Сцилардом, бывшим своим студентом, который впоследствии принял активное участие в Манхэттенском проекте. В тот период он и его более успешный компаньон-изобретатель думали над принципиально новым двигателем для бытовых холодильников. В основе его лежал насос, запатентованный Эйнштейном еще в бытность работы в Швейцарском бюро патентов. Об этой малоизвестной стороне деятельности отца-основателя теории относительности рассказывалось в разделе Лео Сцилард. У большинства обывателей сложилось впечатление об Эйнштейне как универсальном ученом, который внес бесценный вклад во все отрасли необъятной физической науки. С этим я в корне не согласен, в связи с чем хочу заострить внимание нашего читателя на одном наблюдения из своей собственной жизни.

Я знавал одного спортсмена-универсала, которого страшно обожали девушки. Считалось, что он одинаково хорошо играет в коллективные игры с мячом: в баскетбол, волейбол и футбол. Однако я сам играю неплохо в волейбол и могу квалифицированно заявить, что волейболист он был неважный. Потом я заметил, что на футбольное поле он часто выбегал только для того, чтобы покрасоваться перед зрителями. Он довольно мощно и точно бил по воротам, красиво жонглировал мячом, но в ответственных играх никогда не принимал участие. Как я заметил, он больше терся среди тренеров и судей, часто бывал в раздевалке, где давал налево и направо советы начинающим футболистам. Но всё это было несерьезно: мой знакомый был больше актером, чем настоящим футболистом. Что же касается баскетбола, то тут никаких претензий у меня к нему не было, хотя в этом виде спорта я почти не разбираюсь.

Если человек физиологически наделен ловкостью и быстрой реакцией, то многие виды спорта ему подвластны. Для человека, обладающего отменным музыкальным слухом и чувством ритма, открыты широкие возможности играть на многих музыкальных инструментах. Тем не менее, зачастую такие одаренные люди проявляют себя только в одной области музыки или спорта. Это связано с тем, что каждый род деятельности и творчества включает огромный комплекс качеств, которые вырабатываются в течение длительных и упорных тренировок. Мы часто видим, как виртуозный пианист исполняет довольно узкий и однообразный репертуар или как талантливый художник бес конца рисует похожие друг на друга натюрморты.

В общем, наблюдается очевидная тенденция: всякий универсализм так или иначе дается через потерю мастерства в узких областях деятельности. Часто «универсализм» — это только видимость для ограниченных людей; нередко его демонстрируют хитроватые и находчивые люди авантюрного склада ума, которые всю свою сознательную жизнь умело разыгрывают нескончаемую театральную пьесу. Именно таким типом «универсализма» обладал Эйнштейн. Карлу Зелигу он выдал свою секретную «формулу успеха» [5, с. 52]: если успех обозначить через А, то его составляющими будут:

A = x + y + z,

где x — игра, y — работа и z — умение держать язык за зубами. Работа для «Человека ХХ столетия» всегда стояла на втором месте и занимала, как я думаю, не более одного процента. Львиная доля его громкой славы приходилась на актерскую игру, о которой он, конечно, предпочитал помалкивать. В этой связи будет полезно ознакомиться со статьей Наука как форма социальной игры

На рисунке приведена эйнштейновская формула успеха, гласящая, что успех складывается из работы, игры и умения держать язык за зубами. Художник, видимо, не подозревал, каким аморальным человеком он представил здесь Эйнштейна (рисунок взят с сайта www.topcassette.com).

На самом деле, Эйнштейн не сильно нас обманывал, когда написал в «Автобиографических набросках» 1955 года, что он «в физической лаборатории профессора Г. Ф. Вебера работал с рвением и страстью». Сейчас не важно, что он баловался на занятиях, устраивал взрывы и был на плохом счету у ассистента Перне. Важно, что Альберт был человек действия; он не мог, как Милева, сидеть одиноко за письменным столом у себя ли дома или где-нибудь в библиотеке и что-то там теоретизировать. Ему всегда нужна была аудитория, в которой бы он солировал. Одна его знакомая, учившаяся курсом ниже, вспоминала, как Альберт частенько заходил в лабораторию, где проходили занятия ее группы, и, дождавшись, когда ассистент выходил из лаборатории, помогал ей и другим студентам в проведении практической работы. В такие минуты он чувствовал себя на вершине блаженства.

Альберт не был последовательным и напряженным мыслителем; он мыслил кусочно-фрагментарным образом, причем его сильно забавляла парадоксальность, которую он выискивал там, где ее на самом деле не было, нарочно доводя ситуацию до абсурда. Например, его вариант теории относительности возник из выдуманного им еще в студенчестве «парадокса» относительного движения магнита и проводника с током — главных частей двигателя и генератора. Об этом мы поговорим подробно в другом месте, но уже сейчас читатель должен хорошо понимать, что никакого противоречия в работе этих двух взаимно обратных электрических машин нет. Описанные им в начале статьи 1905 года «К электродинамике движущихся тел» ситуация столь же фальшива, как и «парадоксальная» ситуация с поверхностью натяжения, описанная им в начале статьи 1901 года «Следствия из явления капиллярности».

Альберта никогда не интересовало, как реально устроен мир, он был целиком поглощен идеей завоевания этого мира. С младых ногтей он, как и Зигмунд Фрейд, был сориентирован на успех, завоеванный любой ценой — числовой подгонкой, плагиатом или просто обманом. Понимание этой психологической мотивации и всех прочих перечисленных в этом параграфе черт его скверного характера позволяет разграничить в написанных им совместно с Милевой статьях, кто и что именно делал. Вот и сейчас, когда мы обратились ко второй совместно написанной ими статье, не слишком сложно разделить, кто и что в ней писал. Ложную цель статьи, разумеется, сформулировал Альберт, но математические средства ее достижения выбраны были уже Милевой, которую в первую очередь интересовало второе начало термодинамики.

Напомним, в справедливости первого начала термодинамики о невозможности построения вечного двигателя убедились сразу несколько исследователей первой половины XIX века. Второе начало термодинамики гласит: в системе, предоставленной самой себе, тепловая энергия не может передаваться от холодного предмета к нагретому. Его сформулировал Клаузиус в 1850 году по итогам работ Сади Карно. Максвелл и Больцман примерно одновременно около 1870 года пришли к выводу о статистическом характере второго начала. В двух фундаментальных статьях Больцмана 1871 и 1872 года дается соотношение, выражающее равновесие между энтропией, теплотой и температурой, знаменитое уравнение, связывающее энтропию с вероятностью ( S = k ln W, оно начертано на могильной плите Больцмана), и формулируется так называемая H-теорема.

Сразу же в область физики, открытую Карно, Клаузиусом, Максвеллом и Больцманом, ринулось огромное число тогдашних физиков, включая Гиббса, Планка, Вина, Дебая и пр. Сказать, что кто-то в одиночку в начале XX столетия прошел путь, который проделала славная когорта физиков-первопроходцев, равносильно провозглашению себя Колумбом, заново открывшем Америку. Так что эйнштейновские слова: «Не будучи знакомым с появившимися ранее исследованиями Больцмана и Гиббса, которые по существу исчерпывают вопрос, я развил статистическую механику и основанную на ней молекулярно-кинетическую теорию термодинамики». [1, т. 4, с. 275] нужно принимать за характерное проявление мессианского психотипа.

Вторая статья начинается словами:

«Второе начало механической теории тепла можно применять к таким физическим системам, с которыми можно сколь угодно точно совершать обратимые круговые процессы. При этом, в соответствии с выводом второго начала, из невозможности превращения скрытой теплоты в механическую энергию необходимо постулировать, что эти процессы могут быть осуществлены. Однако представляется сомнительным, выполняется ли этот постулат в одном важном случае применения механической теории тепла, а именно: при смешивании двух или больше газов с помощью полупроницаемых перегородок. На предпосылке о реализуемости этого процесса базируются термодинамическая теория диссоциации газов и теория разбавленных растворов» [1, т. 3, с. 18].

Очевидно, материал данной статьи был навеян все тем же учебником В. Оствальда по общей химии, в котором излагалась теория Нернста об электролитических силах внутри диссоциированных электролитов, применимая и к газовым смесям. Некоторое представление об этих физико-химических процессах, происходящих в газовых смесях и слабых растворах, можно получить в разделе Оствальд, Аррениус и Вант-Гофф. В этом случае можно надеяться, что читателю будет понятна следующая постановка задачи на примере двух разновидностей газа:

«...Для каждой пары газов А и В можно изготовить две разделяющие стенки, такие, что одна будет проницаемой для А и непроницаемой для В, а другая — наоборот. Если смесь многокомпонентная, то это предположение выглядит еще более сложным и менее вероятным. Но так как опыт полностью подтвердил результаты теории, хотя мы оперировали процессами, осуществимость которых вызывает серьезные сомнения, то возникает вопрос, нельзя ли применять второе начало к неким идеальным процессам, не вступая в противоречие с опытом.

В этом смысле на основе имеющегося опыта можно высказать во всяком случае следующее положение: согласие с опытом сохранится, если второе начало распространить на физические смеси, отдельные компоненты которых удерживаются в определенных частях пространства с помощью консервативных сил, действующих на некоторых поверхностях. Это положение мы обобщим в виде следующей гипотезы. Согласие с опытом сохранится, если второе начало применить к физическим смесям, на отдельные компоненты которых действуют произвольные консервативные силы» [1, т. 3, с. 18 – 19].

В п. 2, по всей видимости, одна Милева, излагает теоретические положения для решения поставленной задачи. В п. 3 она, вместе уже с Альбертом, описывает некий мысленный эксперимент, логически сильно напоминающий тот, который фигурировал в первой статье.

Берется цилиндрический сосуд, разделенный на два объема I и II, в которых помещены «полностью диссоциированные растворы солей с тождественными ионами металла, но с разными ионами кислотных остатков. Эти две части сосуда соединены промежуточным объемом V, заполненным раствором обеих солей. Предположим, что в V на ионы кислотных остатков действуют силы, потенциалы которых» зависят только от расстояния, но не от сорта или структуры ионов [1, т. 3, с. 22 – 23; и далее с. 27].

Представим себе теперь, что в объемы I и II помещены электроды из металла, соль которого находится в растворе; построим круговой процесс, при котором через систему пропускается количество электричества Е и снова возвращается перенесенное количество металла назад механическим путем, что не требует работы, если предположить равенство гидростатических давлений в объемах I и II. Применяя первое и второе начало термодинамики, получаем

П₂ – П₁ = 0.

Здесь под П₁ и П₂ понимаются электрические потенциалы электродов. Последнее уравнение имеет ту же логическую основу, что и уравнение

(O₂ – O₁)γ₁ – (O₂ – O₁)γ₂ = 0

В п. 4 авторы знакомят читателя с изложенной в статье 1 «теорией консервативных сил», выражающихся известной нам формулой

P = P_∞ – c₁c₂φ(r),

и применяют ее для ионов электролитов. Поскольку данный взгляд на консервативную силу, как уже было выяснено, является ложным, то всё содержание второй статьи тоже оказывается ошибочным. Однако по сравнению с первой статьей вторая выглядит намного предпочтительней, хотя бы потому, что в ней отсутствуют сфабрикованные Эйнштейном числовые массивы. Кроме того, в ней описывается сложная математически осмысленная модель, которую разработала, конечно, Милева Марич.

Вообще, трудно сказать, какие именно фрагменты текста написал лично Эйнштейн — всё выдержано в строго академическом стиле. Похоже на то, что его полностью писала Марич. Только последний абзац не вызывает сомнений — его точно написал инфантильный юноша, который на практических занятиях устраивал в лаборатории взрывы и не слушался ассистента Перне. Вот он: «В заключение я хотел бы извиниться за то, что предлагаю здесь лишь общий план трудоемкого исследования и сам не занимаюсь экспериментом; для этого у меня нет возможностей. Но эта работа всё же достигнет своей цели, если после знакомства с ней кто-нибудь займется экспериментальным исследованием проблемы молекулярных сил» [1, т. 3, c. 33]. Звучит это как-то по-ребячески и заметно выбивается из общего серьезного тона статьи.

Оборотами речи с местоимением «я» типа «я хотел бы извиниться» Милева, очевидно, не пользовалась. Вся вторая статья написана в основном безличными предложениями; иногда встречается местоимение «мы», например: «хотя мы оперировали процессами» [1, т. 3, c. 18], «мы будем основываться на этой гипотезе», «Мы предположим далее» [1, т. 3, c. 19] и т.д. Теперь выпишем несколько характерных фраз из первой статьи: «я буду исходить из простейших предположений» [1, т. 3, c. 10], «Я взял весь материал из книги В. Оствальда по общей химии» (точная ссылка на нее отсутствует), «Я нашел», «Теперь я приведу таблицу» [1, т. 3, c. 12], «Мне кажется» [1, т. 3, c. 13], «на мой взгляд», «ниже таблицы я поместил величины» [1, т. 3, c. 14], «я предпринял попытку», «При этом я исходил» [1, т. 3, c. 15]. Этим не академическим стилем пользовался Альберт. На страницах с математическими формулами подобные местоимения отсутствуют, следовательно, их написала, скорее всего, Милева. Но не лингвистический, а именно математический стиль дает нам верный ориентир на авторство.

Третья статья, написанная одной Марич

Преамбула к третьей статье звучала амбициозно:

Как ни велики достижения кинетической теории теплоты в области физики газов, теория эта до сих пор не имеет под собой удовлетворительной механической основы, поскольку законы теплового равновесия и второе начало термодинамики пока еще не удалось получить из одних только уравнений механики и теории вероятности, хотя Максвелл и Больцман в своих теориях почти достигли этой цели. В настоящем исследовании ставится задача восполнить этот пробел. Одновременно с этим получается обобщение второго начала, имеющее большое значение для применений термодинамики. Кроме того, математическое выражение для энтропии выводится с точки зрения механики.[1, т. 3, с. 34].

Первые пять параграфов статьи 3 можно считать вводными.

1) Механическое изображение физической системы.
2) О распределении возможных состояний между тождественными адиабатическими стационарными системами при почти одинаковом содержании энергии.
3) О (стационарной) вероятности состояний системы S, которая механически связана с системой Σ, обладающей относительно бесконечно большой энергией.
4) Доказательство положительности величины h.
5) О тепловом равновесии.

Шестой параграф «Механическом смысле величины h», который мы полностью процитировали выше, автор просил сравнить с соответствующим местом больцмановских Лекций по теории газов, с которыми Эйнштейн, как мы знаем, в то время не был знаком. Далее шли параграфы:

7) Идеальные газы Абсолютная температура.
8) Второе начало термодинамики как следствие механической теории.
9) Вычисление энтропии.
10) Обобщение второго начала.

Мы процитируем их полностью, чтобы компетентный читатель смог оценить уровень рассуждений автора.

«Развитая теория содержит как частный случай максвелловское распределение по состояниям для идеальных газов. Именно, если в § 3 мы будем понимать под системой S молекулу газа, под Σ — совокупность всех остальных молекул, то для вероятности того, что значения переменных р1,..., рn системы S лежат в бесконечно малой (по отношению ко всем этим переменным) области g, получится выражение

Наше выражение для величины h, найденное в § 3, показывает также, что величина h с точностью до бесконечно малых оставалась бы той же и для молекулы другого газа, находящегося в системе, если только системы Σ, определяющие h для обеих молекул, совпадают с точностью до бесконечно малых величин. Тем самым доказано обобщенное распределение Максвелла для идеальных газов.

Далее получается сразу, что средняя кинетическая энергия движения центра тяжести молекулы газа, находящейся в системе S, равна (3/4) h, так как она соответствует трем импульсам. Но кинетическая теория газов учит, что эта величина пропорциональна давлению газа в постоянном объеме. Полагая давление, по определению, пропорциональным абсолютной температуре, получаем соотношение вида:

где κ — универсальная постоянная, ω — функция, введенная в § 3.

Рассмотрим заданную физическую систему S как механическую систему с координатами р1,..., рn. В качестве переменных состояния в ней введем величины

Пусть Р1,..., Рп — внешние силы, стремящиеся увеличивать значения координат системы. Пусть Vi — потенциальная энергия системы, L — кинетическая энергия, представляющая собой однородную квадратичную функцию p'v. Для такой системы уравнения движения Лагранжа принимают вид:

Внешние силы складываются из двух частей разной природы. Первые из них,

— это те силы, которые представляют условия, налагаемые на систему, и выводятся из потенциала, зависящего только от координат Р1, ..., Рп (например, адиабатические стенки, сила тяжести и т. д.)...

Другие силы, нельзя свести к потенциалу, зависящему только от pv. Силы Пv — это те силы, которые способствуют подводу тепла. Полагая Va + Vi = V, перепишем уравнения движения в виде:

Тогда работа, сообщаемая системе силами Пv за время dt, изображает отнятое за время dt у системы S количество тепла dQ, которое мы будем измерять в механических единицах:

Но так как

и далее

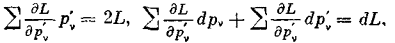
то

Так как

то

      (1)

Займемся теперь выражением

...

Допустим, что бесконечно большое число систем S в стационарных состояниях, которые обладают одинаковыми значениями h и Va, перейдут в новые стационарные состояния, характеризуемые общими для всех систем значениями Символом «δ» будем обозначать вообще изменение некоторой величины при переходе системы в новое состояние, а символом «d» — уже не изменение во времени, а полный дифференциал. Количество систем, переменные состояния которых до изменения находятся внутри бесконечно малой области g, дается формулой

при этом мы можем по своему желанию для каждых заданных значений h и Va выбрать произвольную постоянную V так, что постоянная А будет равна единице. Мы сделаем это для того, чтобы упростить вычисления, и будем обозначать определенную таким образом функцию через V*. Теперь легко видеть, что искомая величина принимает значение

      (2)

причем интегрирование распространяется на все значения переменных. Этим выражением определяется увеличение средней потенциальной энергии системы, которое произошло бы в случае, если распределение по состояниям изменилось бы в соответствии с δV* и δh, а значение V осталось бы неизменным. Далее получаем

(3)

Интегрирование здесь и в дальнейшем проводится по всем возможным значениям переменных. Далее следует учесть, что количество рассматриваемых систем сохраняется. Это приводит к уравнению:

или

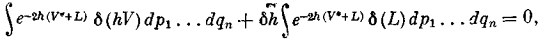
или

      (4)

В (3) и (4) означают средние значения потенциальной и кинетической энергии N систем. Складывая (3) и (4), получаем

или, поскольку

Подставляя эту формулу в (1), находим

Таким образом, dQ/T есть полный дифференциал. Так как

и, значит,

то можно также положить

Следовательно, Е*/Т с точностью до произвольной аддитивной постоянной выражает энтропию системы, причем сделана подстановка Е* = V* + L. Таким образом, второе начало появляется как необходимое следствие механической картины мира.

Найденное для энтропии ε выражение ε = Е*/Т лишь кажется простым; в действительности величина Е* должна вычисляться из механических свойств системы. Именно

причем Е задается непосредственно, а Е₀ как функция Е и h определяется условием:

Итак, получаем

В полученном выражении произвольная постоянная, прибавляемая к величине Е, не влияет на результат, и третий член, обозначенный «const», не зависит от V и Т. Выражение для энтропии ε примечательно тем, что оно зависит только от Е и Т, причем конкретное представление Е в виде суммы потенциальной и кинетической энергии уже не появляется. Это обстоятельство позволяет предполагать, что наши результаты имеют более общее значение, чем использованные механические представления, тем более, что выражение для h, найденное в § 3, обладает таким же свойством.

О природе сил, соответствующих потенциалу Va, не требуется делать никаких предположений. Не требуется даже предполагать, что такие силы существуют в природе. Это значит, что из механической теории теплоты следует, что мы придем к правильным результатам, если будем применять принцип Карно к идеальным процессам, которые получаются из наблюдаемых только путем введения произвольных потенциалов Va. Конечно, результаты, получаемые из теоретического рассмотрения этих процессов, приобретают реальный смысл только тогда, когда идеальные вспомогательные потенциалы Va в них уже не входят.

Берн, июнь 1902 г. Поступила 26 июля 1902 г.» [1, т. 3, с. 44 – 49].

Человек, написавший уравнение

(O₂ – O₁)γ₁ – (O₂ – O₁)γ₂ = 0

и занимающийся дешевой числовой подгонкой никогда бы не смог развить такого рода теорию. Это так же верно, как верно и то, что абстракционист Малевич, нарисовавший «Черный квадрат», никогда бы не смог нарисовать лесной пейзаж как у Шишкина, морскую бурю как у Айвазовского или реалистический портрет как у Репина. Однако продолжим знакомить нашего читателя с последующими статьями по термодинамике.

Четвертая статья, написанная одной Марич

В статье 4, как и в статье 3, Милева сосредоточилась на понятии энтропии и втором начале термодинамики. Если в работе 1902 года, она показала, что понятие энтропии можно вывести просто из кинетических представлений о теплоте, то в работе 1903 года она показала, что это понятие вытекает из «предположений более общего характера» [1, т. 3, с. 50]. В частности, она пришла к выводу:

«Если мы будем следить за рассматриваемыми N системами в течение любого промежутка времени, то распределение состояний, а значит и W, будет постоянно изменяться во времени, и нам придется предположить, что более вероятные распределения состояний всегда будут следовать за менее вероятными, т. е. что W всегда возрастает, пока распределение состояний не станет постоянным и вероятность W — максимальной. В последующих параграфах будет показано, что из этого утверждения можно вывести второе начало термодинамики». [1, т. 3, с. 63].

В связи с этим местом бывший сотрудник Эйнштейна и его биограф, Абрахам Пайс, пишет:

«Эйнштейн … не подозревал об основной тонкости в доказательстве второго закона, а именно о том, что рост энтропии является наиболее вероятным, а не единственно возможным процессом. Лишь в 1910 г. "вывод" Эйнштейна был впервые подвергнут критике. Тогда Пауль Герц отметил, что "если предположить, как это сделал Эйнштейн, будто за менее вероятными всегда следуют более вероятные распределения, то этим вводится особое неочевидное допущение, явно нуждающееся в доказательстве"» [4, с. 71].

Таким образом, Милева ошиблась, думая, что второе начало термодинамики можно получить не из кинематики движения молекул, а из чисто математических соображений. Возможно, она помогла Альберту в дискуссии с П. Герцем, который убедил их обоих в ошибочности постановки задачи, которые решались в статьях 3 и 4. Но скорее всего, она не принимала никакого участия в дискуссии с П. Герцем. Чтобы это понять приведем целиком заметку из «Annalen der Physik» (1911, 34, p. 175 – 176), которая появилась по итогам, подчеркнем, устной дискуссии. В заметке, озаглавленной «Замечания к работам П. Герца: "О механических основах термодинамики"» говорилось:

П. Герц в своих только что названных превосходных работах подверг критике два места моих работ по этому же предмету. Ниже я кратко выскажусь по поводу этой критики, причем замечу, что сказанное здесь является результатом устного обсуждения с П. Герцем, в ходе которого мы пришли к полному согласию по обоим рассматриваемым пунктам.

1. В предпоследнем абзаце § 13 своей второй работы Герц критикует мой вывод закона энтропии для необратимых процессов. Я считаю эту критику совершенно правильной. Мой вывод не удовлетворял меня уже тогда, и поэтому я вскоре опубликовал второй вывод, который также цитируется П. Герцем.

2. Содержащиеся в § 4 его первой статьи 2 возражения против рассмотрения температурного равновесия в первой из упомянутых моих работ основаны на недоразумении, вызванном слишком сжатой и недостаточно тщательной формулировкой этого рассмотрения.

Но так как эта проблема в достаточной мере уже выяснена работами других авторов и обсуждение ее к тому же вряд ли представит особый интерес, я не буду останавливаться на этом вопросе. Замечу только, чтог по-моему, следует предпочесть предложенный Гиббсом в его книге путь, исходным пунктом которого является канонический ансамбль. Если бы книга Гиббса была мне известна в то время, я вообще не стал бы публиковать упомянутые работы, а ограничился бы рассмотрением некоторых частных вопросов.

Цюрих, октябрь 1910 г. Поступила 30 ноября 1910 г.»
[1, т. 3, с. 252].

М. Марич и А. Эйнштейн, фото 1910 года.

В этом ответе обескураживает следующее обстоятельство, на которое обратил внимание Пайс. Последний пишет: «За месяц до ответа Герцу Эйнштейн вполне правильно сформулировал второй закон в другой статье. Можно лишь заключить, что, отвечая Герцу, он был не очень внимателен» [4, с. 71]. Далее Пайс цитирует указанную статью, против которой у Герца уже не было бы критических возражений.

Однако, что значит «был не очень внимателен»? Как можно забыть свою собственную статью, поступившую в «Annalen der Physik» 8 октября 1910 года, в которой дается со статистической точки зрения вполне корректная формулировка второго начала (закона) термодинамики?

Эта статья имеет порядковый номер 22 и называется «Теория опалесценции в однородных жидкостях и жидких смесях вблизи критического состояния» (1910, 33, 1275 – 98). С точки зрения математики, она довольно сложна и написана по следам статьи Мариана Смолуховского (1872 – 1917), теоретический подход которого тесно переплетался с подходом, предложенным Милевой Марич в статье 4. Видимо, при чтении статьи Смолуховского 1908 года, опубликованной в 25 выпуске «Annalen der Physik», она поняла ошибочность своего прежнего подхода и аккуратно, чтобы не сильно бросалось в глаза, внесла нужные коррективы, о которых, однако, не знал Эйнштейн. Этим только и можно объяснить недоразумение, на которое указал Пайс.

Между прочим, в ответе Эйнштейна Герцу имеется еще одна загадка, носящая уже психологический оттенок. Не понятно, зачем автор заметки специально оговаривается: «сказанное здесь является результатом устного обсуждения с П. Герцем». Пайс со слов Карла Зелига [5] замечает: «Но переписка Эйнштейна с Герцем происходила в 1910 г., когда Эйнштейн был профессором в Цюрихе (в летний семестр этого года читал курс лекций по кинетической теории теплоты). К этому времени (как упоминалось выше), он уже прочел работу Больцмана 1877 г., в которой утверждалось, что энтропия растет не всегда, а почти всегда» [4, с. 71].

По всей видимости, дискуссия велась и устно, и письменно. Но как-то уж очень легко Альберт расстался с теоретической позицией двух фундаментальных статей, на которые Милева потратила, очевидно, не один год кропотливой работы. Ответ Герцу выглядит не просто лаконичным, а каким-то скомканным. Складывается впечатление, что между ним и Герцем была заключена устная договоренность: он отказывается от своей (разумеется, Милевы) теоретической точки зрения, а Герц обещал, видимо, более не будировать данную тему. Если бы дискуссию с Герцем вела Милева, она бы ни за что не сдала бы свою теоретическую позиции. Это становится особенно ясна в свете затронутых ею вопросов, рассмотренных в октябрьской статье 1910 года.

Милева Марич — гений

Фильм сербского телевидения с моим скромным участием

(Продолжение следует)

---

1. Эйнштейн А. Собрание научных трудов в 4-х томах. / Под ред. И.Е. Тамма, Я.А. Смородинского и Б.Г. Кузнецова. — М.: Наука, 1965.
2. Борн М. Альберт Эйнштейн и световые кванты / УФН, т. LIX, вып. 1, май, 1956, с. 119 – 134.
3. Хофман Б., Дюкас Э. Альберт Эйнштейн. Творец и бунтарь. — М.: Прогресс, 1983. (Banesh Hoffmann/Helen Dukas: Einstein. Schopfer und Rebell . Die Biographie, Frankfurt/M. 1978, amerikanisches Original New York, Viking Press, 1972).
4. Пайс А. Научная деятельность и жизнь Альберта Эйнштейна. — М., 1989 / Pais A. Subtle is the Lord... The Science and the Life of Albert Einstein (Oxford: Oxford Univ. Press, 1982).
5. Зелиг, Карл. Альберт Эйнштейн. – М.: Атомиздат, 1964.
6. The Collected Papers of Albert Einstein (CPAE). Volume 1. The Early Years, 1879-1902, Princeton University Press 1987.