Олег Акимов

Вихри. Аэродинамика Теодора фон Кармана

В 1953 году, когда исполнился полувековой юбилей полетов человека на аппаратах тяжелея воздуха, вышла книга Теодора фон Кармана (1881 – 1963) под названием «Аэродинамика. Избранные темы в их историческом развитии» [1]. Она написана на основе шести Мессенджеровских лекций, прочитанных автором в рамках цикла просветительских чтений «О развитии цивилизации», организованных в 1923 году Хайремом Дж. Мессенджером.

Карман является наиболее известным теоретиком первой половины 20-го столети в области аэродинамики. Он родился и вырос в еврейской семье, проживавшей на венгерской территории Австро-Венгерской империи. В 1902 году закончил Будапештский университет и вскоре переехал в Германию. В 1908 году под руководством Людвига Прандтля защитил докторскую диссертацию по аэродинамике. Защита проходила в Гёттингенском университете, где он и остался работать. Позже ему предложили возглавить Институт воздухоплавания при Аахенском университете. Участвовал в Первой мировой войне в рядах австро-венгерской армии.

Теодор фон Карман

В 1930 году его пригласили в Калифорнийский технологический институт. Приехав туда, он возглавил лабораторию воздухоплавания. В 1936 году стал работать в компании Аэроджет, разрабатывающей и выпускающей ракетные двигатели. В 1940-е годы переключился на космическую тематику. В 1944 успешно перенес онкологическую операцию на кишечнике. По его инициативе в 1960 году основана Международная академия астронавтики, объединяющая ведущих ученых, работающих в области космических исследований. Карман умер в 1963 году во время поездки в Аахен (Германия); похоронен в Пасадене (Калифорния).

Названная книга интересна в двух отношениях. Первая причина состоит в том, что она демонстрирует необходимость и важность практики наряду с теорией. У кого-то, возможно, сложилось впечатление, будто первоначально зарождаются теоретические идеи, которые затем находят приложения в нашей практической жизни. Однако вся история науки демонстрирует скорее обратную последовательность этих двух познавательных компонентов. Верно, что толчком к любой практической деятельности, является некая идея. Но обычно она слишком сыра: в процессе конструирования машины или прибора ее изначальный блеск быстро тускнеет. Настоящая, строго формализованная теория возникает после множества итерационных шагов обдумывания и деланья. Классическим примером здесь может служить наука об электромагнетизме. Сначала ей предшествовала длинная череда нехитрых опытов, которую венчает сложная серия экспериментов, проведенная Фарадеем. На его опытной базе Максвелл разрабатывает теорию, которая имела слишком абстрактный вид. Эдисон, Тесла и прочие практикующие физики в течение нескольких десятилетий корректируют и конкретизируют данный раздел науки.

Релятивистская физика демонстрирует нам сильно искаженное развитие некой области знаний, которая насквозь пронизана философскими и математическими спекуляциями. Кивнув в сторону сторонников теории относительности и квантовой механики, Карман многозначительно и не без иронии заметил: «Мы, специалисты по аэродинамике, всегда скромнее и не пытаемся изменить основные представления человеческого разума или вмешаться в дела милостивого Господа и божественного Провидения!» [1, с. 11].

Аэро- и гидродинамика, как и механика в целом, постоянно напоминают нам о большом влиянии эмпирии на формирование теории. Какой бы раздел науки мы ни взяли — будь то механика или электромагнетизм — деление ее на прикладную и фундаментальную легко обнаруживает себя. Но вот космология, возникшая на базе релятивистской и квантовой механики, состоит преимущественно из фундаментальной части. По причине отсутствия в ней сколько-нибудь значительного прикладного раздела она выглядит как бы и не наукой, а некой философией, которая путем недобросовестных рассуждений, в принципе, чуждых настоящему физику, внедрилась в тело естествознания и заняла в нем чуть ли не главенствующее положение. Непосвященных в ее проблемы людей сложные математические модели, рассчитанные на высокоскоростных компьютерах, могут сбить с толку. Но специалисты прекрасно знают, что подобные компьютерные расчеты часто служат источником еще худшей схоластики.

Космология рассматривает процессы и явления, затрагивающие вселенную в целом. Космологи традиционно много фантазируют по поводу Большого Взрыва, черных дар и нор, которые тесно связаны с релятивистской физикой и квантовой механикой. Именно эти два раздела придают космологии фантасмагорический характер. Правда, в последнее время в связи с развитием телескопических инструментов, работающих в различных диапазонах излучения, космологи стали большое уделять внимание наблюдениям космических объектов. Несмотря на это большинство нынешних космологов по-прежнему очень далеки от тех нерешенных в течение прошлого века проблем, которые лежат в основаниях их чудной науки. Например, они утверждают, что в центре большинства спиральных галактик находятся черные дыры, связанные с «искривлением пространственно-временного континуума» (рис. 1; более подробно о черных дырах можно прочитать здесь ).

Рис. 1. Портрет Стивена Хокинга,
над головой которого изображена система типа SS 433,
состоящая из звезды и черной дыры, вокруг которой
виден аккреционный диск и пара джетов

Прозаически настроенные астрономы воспринимают черные дыры более рациональным и естественным образом. Для них эти, некогда экзотические объекты, практически потеряли релятивистскую сущность. Черная дыра для здравомыслящего астронома 21-го века это уже не сингулярная точка, являющаяся входом в другую вселенную, в которой пропадает свет и вещество нашей вселенной. Наоборот, являясь сверхплотным сгустком материи, «дыра», окруженная аккреционным диском, предстается ему мощным источником жесткого космического излучения, лучи (джеты) которого, как правило, направлены перпендикулярно к плоскости спиральной или сплющенной галактики. В таком вполне классическом понимании данного космического феномена уже нет ничего странного. Понятно, что в нетвердых средах поступательное движение (дивергенция, div) может вызывать вращение (ротацию, rot), и наоборот.

Рис. 2. Дивергенция в жидкой или газообразной среде
может вызывать ее ротацию, и наоборот

Исследователь, который в молодые годы не поленился разобраться в спекуляциях релятивистов и осознал неэтичное поведение Эйнштейна в науке, скорее применит аэро- и гидродинамические модели к упомянутым «черным дырам». Надо хорошо усвоить, что никакого влияния гравитационного поля на ход световых лучей не было никем зафиксировано. Результаты наблюдений звездного неба вблизи затемненного Луной солнечного диска были сфальсифицированы (см. раздел: Отклонение лучей света вблизи массивных тел ). Но этим фальшивым фактом релятивисты третировали физиков-классиков (в нашей стране это были Кастерин, Тимирязев, Миткевич, Предводителев ) и прервали нормальное развитие газодинамики в применении к микро- и макромиру. В этой связи будет не лишним погрузиться не только в историю развития аэродинамики, рассказанную в книге Кармана [1], но и хорошо усвоить основное содержание данного раздела физики.

*
*   *

До аэродинамической науки существовала наука аэростатическая. Бенджамин Франклин (1706 — 1790) был, вероятно, одним из первых, кто размышлял над постройкой аэростата. Принцип поддержания аэростата или дирижабля в воздухе, основывается на известном статическом законе Архимеда. Относительно жидкости закон гласит: каждое тело, погруженное в жидкость, теряет столько своего веса, сколько весит вытесненная им жидкость. Это означает, что тела, удельный вес которых, меньше удельного веса жидкости, будут плавать на поверхности жидкости. Например, пробка и жир плавают на поверхности воды. Данный закон распространяется и на газы. Еще Демокрит понимал, что огонь стремится подняться вверх, потому что его удельный вес меньше удельного веса воздуха.

Джордж Кейли

Зачаточные идеи аэродинамики, заключающиеся в поддержании летательного аппарата в воздухе с помощью винта и машущих крыльев, как у птиц, тоже существовали с незапамятных времен. Достаточно вспомнить выполненный рукой Леонардо да Винчи чертеж «вертолета», в котором использовался так называемый винт Архимеда (рис. 3). О крыльях можно и не говорить: немало смельчаков, привязав к рукам крылья и бросившись вниз головой с колокольни, сломали себе шею и конечности. Карман назвал англичанина сэра Джорджа Кейли (1773 – 1857), кто в своих статьях периода 1809 – 1810 гг. впервые серьезно заговорил о поддержании летательных аппаратов «с помощью движущихся наклонных поверхностей в направлении полета, при условии, что у нас есть механическая энергия, чтобы уравновесить сопротивление воздуха, препятствующего этому движению» [1, с. 15].

Рис. 3. "Вертолет" Леонардо да Винчи

Кейли писал: «С помощью эксперимента установлено, что для уменьшения сопротивления форма задней части веретена имеет не меньшее значение, чем форма передней его части». «Однако я боюсь, — продолжал он, — что вся эта тема такая неясная по существу, что ее полезнее исследовать с помощью эксперимента, чем на основе рассуждений [под этим он, несомненно, понимал теоретическое обоснование], и в отсутствие любых убедительных доказательств того и другого единственный остающийся способ — это копирование природы; поэтому я приведу в качестве примера тела форели и вальдшнепа» (рис. 4) [1, с. 16 – 17].

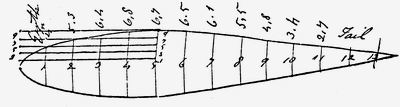
Рис. 4. Летательный аппарат Джоржа Кейли,
имеющий форму форели.

И действительно, до первого полета братьев Райт в 1903 году математика и теоретическая физика были абсолютно бессильны в деле проектирования летательных аппаратов тяжелея воздуха. «Уилбер (1867 – 1912) и Орвилл (1871 – 1948) Райт не были профессиональными учеными. Однако они были знакомы с практическими идеями в области аэродинамики, разработанными до них различными исследователями, и, кроме замечательного таланта конструкторов, у них была возможность использовать эксперименты с моделями для своей натурной конструкции. Фактически для этой цели они использовали простую и малогабаритную аэродинамическую трубу. Более того, они выполнили почти тысячу полетов на планере» [1, с. 33].

Карман знакомит нас с историй развития теоретической аэродинамики, следы зарождения которой можно отыскать в «Началах» Ньютона [книга II, раздел VII, предложение 33]: «…Силы, действующие на два геометрически подобных тела, которые двигаются в жидкостях с различной плотностью, пропорциональны: а) квадрату скорости; б) квадрату линейных размеров тела, и в) плотности жидкости» [1, с. 18]. Так как «скорость изменения количества движения (количество движения = масса × скорость), созданного в жидкости, пропорциональна плотности жидкости и квадрату скоростей отдельных частиц, вовлеченных в движение, поэтому, при условии подобия течения, она пропорциональна квадрату скорости невозмущенного потока жидкости» [1, с. 18 – 19]. Отсюда возникает формула:

F = ρ ( SU )² sin² α,             (1)

«где ρ — плотность жидкости, S — площадь пластины, U — скорость пластины [или строи воздух относительно покоящейся пластины], α — угол наклона [угол атаки]. Сила F направлена перпендикулярно поверхности. Величина ρSUsin α несомненно является потоком массы в единицу времени через поперечное сечение S sin α, равное проекции пластины, перпендикулярно первоначальному направлению течения (рис. 5). Предполагается, что после столкновения частицы следуют по направлению пластины. Затем получаем изменение количества движения массы жидкости, попадающей на пластину в единицу времени, умножив эту массу на составляющую скорости Usin α, возникающую вследствие столкновения» [1, с. 19 – 20].

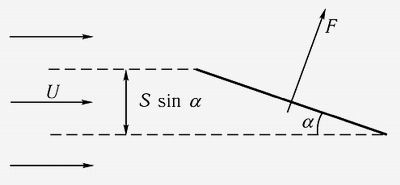
Рис. 5. Чертеж, разъясняющий выражение (1).

Далее Карман рассказывает о многочисленных экспериментах, которые заканчиваются следующим выводом: «Экспериментальные данные показали, что три утверждения Ньютона оказались верными: пропорциональность плотности, пропорциональность квадрату линейного размера и пропорциональность квадрату скорости. … Прогноз Ньютона о пропорциональности между силой, действующей на элемент поверхности, и квадратом синуса ее угла наклона оказался совершенно ошибочным. Эксперименты доказали, что сила скорее почти линейна синусу угла или самому углу в случае малых углов» [1, с. 25].

Такой неприятный результат заставляет нас думать, что произведение SU является потоком, который невозможно разложить на две независимых величины — S и U. Поэтому в вертикальной проекции потока синус фигурирует только в первой степени:

F = ρ ( SU )² sin α,             (2)

Но эти рассуждения и формула (2) являются ошибочными, поскольку эксперименты показали, что процесс обтекания пластины воздухом или жидкостью не сталь прост, как может показаться на первый взгляд. Здесь возникают вихри, которые не могут быть описаны выражениями типа (1) и (2). Но об этой стороне дела поговорим потом. Сейчас нам важно заострить внимание читателей на познавательных вопросах философского значения.

В связи с тем, что «теория расходилась с фактами», причем самым вызывающим образом, Карман написал: «Некоторые авторы высказали мнение, что закон Ньютона способствовал пессимистическим прогнозам по поводу возможностей полета с работающим двигателем, которые можно найти в научной литературе. Лично я не считаю, что влияние Ньютона было действительно таким катастрофическим. Полагаю, что большинство людей, которые в тот ранний период, о котором мы говорим, были действительно заинтересованы в полетах, не верило ни в одну теорию. …

На всем протяжении девятнадцатого века мы наблюдаем два практически не связанных процесса. С одной стороны, энтузиасты полетов, в основном практичные люди, развивали свои собственные довольно примитивные теории полета птиц и пытались применить свои выводы к требованиям полета человека. С другой стороны, представители науки развивали математическую теорию динамики жидкостей; это развитие не имело отношения к проблеме полета и не дало много полезной информации тем, кто стремился летать» [1, с. 26].

История развития самолетостроения убедительно доказывает, какой огромный разрыв может возникнуть между теоретическими построениями и реальными процессами, которые, казалось бы, должны в точности описываться вполне очевидными математическими выражениями. В связи с этим чудовищным расхождением теории и практики не перестаешь удивляться самоуверенности релятивистов.

В самом деле, никто из них не в состоянии теоретически описать явления, ежесекундно протекающие внутри и на поверхности Солнца — даже очень и очень приблизительно. Но они самонадеянно заявляют: «Мы не знаем и не хоти входить в многочисленные детали сложного физического процесса, но мы точно знаем, что произойдет со звездой в целом». Например, релятивисты дают стопроцентную гарантию тому, что Солнце превратится в черную дыру, если его радиус уменьшить до 3 км. Черная дыра с массой в 10 Солнц будет иметь радиус 30 км, в 100 Солнц — 300 км, а в 1000 Солнц — 3000 км. Всё очень просто!

В эти цифры может поверить человек, лишенный всякого критического мышления. Наукой ему лучше не заниматься. Формулу для радиуса черной дыры вывел Карл Шварцшильд, спустя несколько месяцев после того, как Эйнштейн опубликовал свои гравитационные уравнения. Еще никто не доказал, что невесомые фотоны будут отклоняться в поле тяготения — положение само по себе абсурдное — а релятивисты уже вывели формулы радиуса черной дыры, если она вращается, имеет магнитное поле и на ее поверхности равномерно "размазан" электрический заряд.

И это притом, что никто не знает, почему угловые скорости вращения Солнца вблизи экватора и вблизи полюсов сильно различаются, как распределены электрические заряды и магнитные поля на поверхности бурлящего светила, что влияет на появление темных пятен и протуберанцев. Но релятивисты-популяризаторы зря времени не теряли. Они уже издали миллионными тиражами свои бредовые книжки с картинками, где детально рассказывают наивным юношам, что увидит космонавт Вася, когда начнет проваливаться в черную дыру.

Почитайте книгу Уильяма Дж. Кауфмана «Космические рубежи теории относительности» и вы удивитесь, сколько вздора можно выдумать, оттолкнувшись от тривиального факта равенства инерционной и гравитационной массы. В водном тексте можно прочитать характерную для релятивисткой космологии фразу: «Эта книга была написана 25 лет назад, уже в то время теория черных дыр продвинулась в своем развитии в такие дали, куда не скоро сможет "добраться" эксперимент». Автору этих строк невдомек, что вне эксперимента никакая наука существовать не может.

Черная дыра — это фантом, который первоначально возник из вполне понятного положения: если гравитационная масса искривляет лучи света, то существует поле тяготения такой силы, что лучи замкнутся на поверхность тела, генерирующее это поле. Как уже говорилось, в 1919 году были сфальсифицированы результаты солнечного затмения, в которые релятивисты поверили. А дальше пошло-поехало...

Сначала черные дыры искали в тех частях ночного неба, где не было видно звезд. Но по ходу усовершенствования техники наблюдения за звездами, таких мест на небе почти не осталось. Тогда релятивисты решили, что черные дыры скрываются в центрах галактик. Поскольку из этих центров исходило мощное космическое излучение, они вопреки первоначальному определению стали уверять, будто это излучение как раз и свидетельствует о наличие в тех местах черных дыр. Кроме того, черной дырой у них заканчивается эволюция обыкновенной звезды, когда она пройдет фазу белого карлика и нейтронной звезды (подробности здесь ).

*
*   *

Но оставим в покое славных релятивистов с их черными дырами и вернемся к истории науки о вихрях. Вся книга Кармана [1] посвящена, собственно, анализу инженерных конструкций, которые повлияли на формирование аэродинамической теории. Ниже приведено несколько пассажей из нее на данную тему.

«В длинном перечне экспериментаторов, инженеров и физиков, — пишет Карман, — мы найдем имена многих известных ученых. Эдм Мариотт (1620 – 1684) измерил силу, действующую на плоскую пластину, погруженную в поток воды. Эксперименты Жана Шарля де Борда (1773 – 1799) включали тела различной формы; он приводил тела в движение в воде с помощью вращающегося рычага, так называемой карусельной установки. Этот метод ранее применял Бенджамин Робине (1707 – 1751), который выполнял свой эксперимент в воздухе. …

При измерении сопротивления тела, для которого применяли его прямолинейное протаскивание в жидкости, использовалось несколько экспериментальных методов. Жан Лерон Даламбер (1717 – 1783), Антуан Кондорсе (1743 – 1794) и Шарль Боссю (1730 – 1814) буксировали модели кораблей в стоячей воде. Возможно, это было первым применением так называемого метода буксировочного бассейна. Для перемещения моделей в прямолинейном движении по воздуху использовали локомотивы, а позднее автомобили. Однако этот метод не очень точен. Во-первых, им можно пользоваться только в отсутствие ветра, и, во-вторых, очень трудно вычислить влияние дна.

Еще один метод создания прямолинейного движения — свободное падение тела в воздухе. Ньютон сам наблюдал за сферами, падающими с купола собора Святого Павла. Этот метод применяли многие исследователи. Замечательные эксперименты проводили в конце девятнадцатого и начале двадцатого века Александр Густав Эйфель (1832 – 1923).

Лучший метод для измерения сопротивления воздуха — поместить модель в искусственный поток воздуха, т. е. метод аэродинамической трубы. Первым человеком, создавшим подобную установку, был Франсис Герберт Уэнем (1824 – 1908), член-учредитель Общества по аэронавтике Великобритании, разработавший в 1871 году аэродинамическую трубу для этого Общества. В 1884 году другой англичанин, Горацио Филлипс (1845 – 1912), построил усовершенствованную аэродинамическую трубу. Вслед за ними было построено еще несколько небольших аэродинамических труб; например, в 1891 году Николай Егорович Жуковский (1847 – 1921) в Московском университете построил трубу два фута в диаметре.

В первом десятилетии нашего века аэродинамические трубы были построены почти во всех странах. Среди строителей были Стантон и Максим в Англии, Рато и Эйфель во Франции, Прандтль в Германии, Крокко в Италии, Жуковский и Рябушинский в России. По сравнению с современными огромными трубами эти установки были сравнительно скромными. Например, ни у одной аэродинамической трубы, построенной до 1910 года, мощность не превышала 100 лошадиных сил. Сегодня аэродинамическая труба во французских Альпах использует гидравлическую энергию до 120 000 лошадиных сил» [1, с. 20 – 24].

Карман отметил также заслуги Шарля Ренара (1847 – 1905), Этьена Жюля Маре (1830 – 1904), братьев Отто (1848 – 1896) и Густава (1849 – 1933) Лилиенталей, Альфонса Пено (1850 – 1880), Самюэля П. Лэнгли (1834 – 1906), Чарльза М. Мэнли (1876 – 1927) и Себастьяна Финстервальдера (1862 – 1951).

В теоретическом плане тоже были сделаны важные заделы. В этой связи необходимо отметить прежде всего работу Даниила Бернулли 1738 года «Гидродинамика, или комментарии о силах и движениях жидкостей». Основываясь на законе сохранения живой силы (кинетической энергии), он установил связь между давлением, уровнем и скоростью движения жидкости. В «Трактате о равновесии и движении жидкостей» (1744) и особенно в «Очерке новой теории сопротивления жидкостей» (1752) Даламбер пришел к парадоксальному выводу. Карман в разделе «Математическая механика жидкостей» об этом парадоксе рассказал следующим образом.

Жан Лерон Даламбер

«После публикации теории Ньютона математики признали недостатки его метода. Они поняли, что задача не так проста, как полагал Ньютон. Мы не можем заменить течение параллельным движением, как пытался это сделать Ньютон приближенным образом (рис.5). Первым человеком, который разработал то, что мы можем назвать точной теорией сопротивления воздуха, был Даламбер, великий математик и один из энциклопедистов Франции. Он опубликовал свои открытия в книге под названием Очерк о новой теории сопротивления жидкостей. Несмотря на свой значительный вклад в математическую теорию жидкостей, он получил отрицательный результат. Он заканчивает следующим выводом:

Допускаю, что в таком случае я не вижу как можно объяснить удовлетворительным способом сопротивление жидкостей с помощью теории. Напротив, мне кажется, что эта теория, рассмотренная и изученная с глубоким вниманием, дает, по крайней мере, в большинстве случаев абсолютно нулевое сопротивление; необычайный парадокс, который я предоставляю объяснить геометрам.

Это утверждение, — продолжает Карман, — мы сейчас называем парадоксом Даламбера. Он означает, что чисто математическая теория приводит к выводу: если мы перемещаем тело по воздуху и пренебрегаем трением, то тело не встречает сопротивления. Очевидно, что этот результат не смог оказать значительную помощь конструкторам-практикам.

       

Портреты ученых-физиков (слева направо):
Джон Уильям Стретт (лорд Рэлей), Герман фон Гельмгольц и Густав Кирхгоф

В следующем веке Гельмгольц, Густав Кирхгоф (1824 – 1887) и Джон Уильям Стретт, лорд Рэлей (1842 – 1919) разработали теорию, которая, как они полагали, даст нам возможность избежать вывода Даламбера. Эта теория описывает движение наклонной пластины особенным способом, предположив, что поверхность разрыва образуется на каждой кромке пластины, так что за пластиной следует спутная струя, состоящая из "застойного воздуха" и расширяющаяся до бесконечности позади пластины (рис. 6). Это допущение позволяет рассчитать силу, действующую на пластину, отличную от нуля даже в случае невязкой жидкости» [1, с. 34].

На рис. 6 показана наклоненная плоскость крыла и струи воздуха, которые дуют под крыло и обтекают крыло сверху и снизу так, что над плоскостью крыла образуется «застойная воздушная зона».

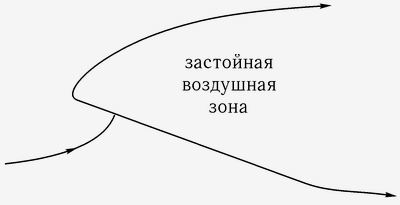
Рис. 6. Струи воздуха вблизи плоскости крыла,
согласно теории Рэлея, в которую внесли определенный
вклад Гельмгольц и Кирхгоф

К сказанному добавим следующий пассаж:

В трактате "Гидродинамика" (1738) Д. Бернулли, основываясь на законе сохранения живой силы, установил связь между давлением, уровнем и скоростью движения жидкости. Через пять лет Ж. Даламбер в "Трактате о динамике" впервые сформулировал общие правила составления дифференциальных уравнений движения любых материальных систем, сводя динамические задачи к статическим. Этот же принцип применен им для обоснования гидродинамики в трактате "Рассуждения об общей причине ветров".

Л. Эйлер в трактате "Общие принципы движения жидкостей" (1755) впервые вывел систему уравнений движения идеальной жидкости. Этим трактатом было положено начало аналитической механики сплошной среды. Им было введено также понятие потенциала скоростей. Методы Эйлера и Даламбера были усовершенствованы Лагранжем. Лагранж (1781) нашел динамические условия, выполнение которых обусловливает существование безвихревого движения с потенциалом скоростей. Лагранж установил, что вихри не могут возникнуть в лишенной вязкости жидкости, если их в ней с самого начала не было. Если же вихри были, то они не могут быть уничтожены.

В 1815 году Коши строго доказал теорему Лагранжа. Разработка методов решения эйлеровых уравнений движения идеальной жидкости характерна для гидромеханики первой половины XIX века. К этому же времени относится появление гидродинамики вязкой жидкости. В 1858 году вышла работа Гельмгольца "Об интегралах уравнений гидродинамики, соответствующих вихревым движениям", в которой заложены были основания теории вихрей. Это исследование — крупнейшее достижение гидродинамики со времен Эйлера и Лагранжа [2, с. 225 – 226].

О внесенных Гельмгольцем новшествах рассказывается в разделах Гельмгольц. Часть 1 , часть 2 , часть 3 .

На графике (рис. 7) изображены три кривых, отвечающих трем аэродинамическим теориям: 1 — Ньютона, 2 — Рэлея и 3 — Кармана. Последнюю кривую автор книги [1] назвал соответствующей «современной теории подъемной силы» или теории циркуляции. По оси абсцисс откладывается угол атаки, т.е. угол наклона плоскости крыла; по оси ординат — сила, для удобства представленная в единицах ρ U ² L, где ρ — плотность жидкости, U — скорость относительного потока и L — ширина плоскости крыла.

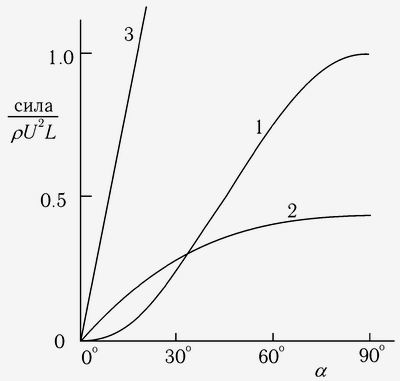
Рис. 7. Три кривых для подъемной силы,
отвечающих теориям Ньютона, Рэлея и Кармана

С количественной точки зрения теория Рэлея и его двух замечательных предшественников — Гельмгольца и Кирхгофа — отвечала реальной ситуации еще меньше, чем теория Ньютона. Однако она учитывала вполне фиксируемый в эксперименте результат, связанный с возникновением особой зоны над крылом. Кроме того, она преодолевала парадокс Даламбера. Напомним, согласно этому парадоксу выходило, что тело, равномерно движущееся в идеальном потоке, не испытывало никакого сопротивления. Под идеальной средой понималась «математическая» среда газовой или жидкой консистенции, лишенная вязкости. Эта проблема 18-го века поставила в тупик теоретиков 19-го века, которые, однако, ее не решили.

Итак, повторим, по теории Ньютона плоскость крыла «рубила» своими краями движущиеся струи, что давало значительное расхождение с опытом. По теории Даламбера, который рассматривал абсолютно обтекаемое тело, наподобие «форели» Кейли (рис. 4), поток нигде не прерывался, что реально для плоского крыла не выполнялось. По теории Рэлея «отрыв» потока от движущегося крыла был предусмотрен, но результат ее оказался тоже ошибочным: рассчитанные по ней сопротивление и подъемная сила не соответствовали экспериментальным данным. Адекватная аэродинамика возникла только в 20-м веке, когда теоретики и практики стали работать в тесном содружестве. Теодор фон Карман был тем замечательным исследователем, в котором совмещался талант вдумчивого теоретика и наблюдательного практика.

*
*   *

До сих пор речь шла о расхождениях теории и эксперимента в рамках решения задачи о движении летательных аппаратов. Но тот же Рэлей в 1878 году опубликовал статью, в которой рассматривалась задача, которая на первый взгляд никак не связанная с самолетостроением. Рассмотренный в ней случай лишний раз опровергал парадоксальный вывод, сделанный Даламбером более ста лет тому назад. Рэлей установил: если цилиндр омывается спокойным горизонтальным потоком (рис. 8а), то его французский предшественник, в принципе, прав. Если при этом заставить цилиндр вращаться, то возникнет дополнительная сила, перпендикулярная потоку, которая заставляет цилиндр отклониться вверх (рис. 8б).

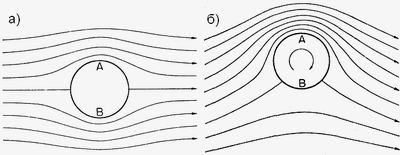Рис. 8. Покоящийся цилиндр погружен в равномерно текущий поток (а). За счет симметричного давления на поверхность цилиндра, последний начнет перемещаться по горизонтали слева направо, т.е. сноситься потоком. Если цилиндр заставить вращаться по часовой стрелке, то на него будет действовать дополнительная вертикальная сила, выталкивающая цилиндр наверх (б).

Откуда взялась перпендикулярная потоку сила? В верхней точке A к скорости горизонтально текущего потока прибавляется скорость циркуляции цилиндра и, таким образом, поверхность цилиндра оказывает либо меньшее сопротивление потоку, либо еще больше ускоряет его. В нижней точке B происходит вычитание скоростей, что равносильно возрастанию сопротивления. Цилиндр будет двигаться по пути наименьшего сопротивления потоку, которое окажется сверху от цилиндра. Даниил Бернулли (1700 – 1782) доказал теорему для идеальной несжимаемой жидкости: чем выше скорость потока, тем ниже давление в нём, и наоборот.

Итак, опыт Рэлея однозначно связан с величиной сцепления потока с жесткой поверхностью цилиндра, которую можно охарактеризовать также термином трение. В точке A трение минимально, в точке B оно максимально. Величина трения, сцепления или сопротивления действуют на цилиндр так, что вблизи точки A давление потока на цилиндрическую поверхность оказалось меньше, чем в близи точки B. Отсюда рукой подать до понятия застойной воздушной зоны, показанной на рис. 6, и понятия подъемной силы, пропорциональной разности давлений сверху и снизу плоскости крыла. Первоначально, как мы знаем, эти понятия не связывались с циркуляцией, введенной Рэлеем.

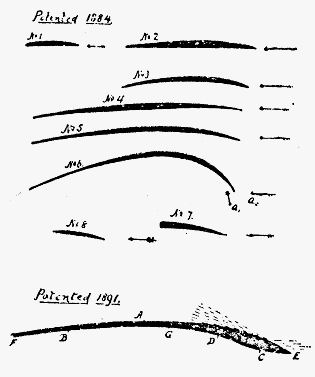
Рис. 9. Изогнутые профили крыльев,
проанализированные Горацио Филлипсом

В конце века Гораций Филлипс эмпирическим путем с помощью аэродинамической трубы установил, что наибольшую подъемную силу развивают крылья с выпуклой поверхностью, как это показано на рис. 9, причем передняя и задняя точки крыла должны находиться, по возможности, на одном уровне, т.е. при нулевом угле атаки.

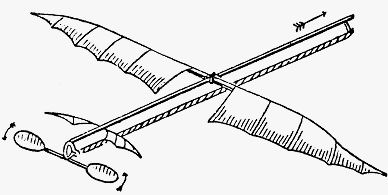
Рис. 10. Модель самолета, предложенная Альфонсом Пено

Выводы Филлипса подтвердил также Герман фон Гельмгольц, изучавший строение птичьих крыльев, и Отто Лилиенталь, экспериментировавший с крыльями планеров. Чтобы придать конструкции самолета большую устойчивость, Альфонс Пено, наряду с оптимальной формой крыльев, приделал к фюзеляжу своей модели хвостовое оперение и там же на хвосте расположил тягловый пропеллер (рис. 10).

Фредерик Ланчестер

Первым, кто отчетливо осознал тесную связь между циркуляций и подъемной силой был, по-видимому, английский инженер Фредерик У. Ланчестер (1878 – 1946), проектировавший и конструировавший автомобильные двигатели. В 1899 году он стал управляющим компании по выпуску легковых автомобилей. Но, будучи человеком разносторонним, он еще в 1894 году начал разрабатывать теорию циркуляции, а в 1907 и 1908 гг. вышли две его книги на эту тему.

У него возникла мысль, — пишет Карман, – что если крыло посредством своего движения создает циркуляцию вокруг себя, которую он назвал "периптерическим движением", то в таком случае оно должно действительно вести себя как вихрь, т. е. возбуждать поле течения, также как это сделал бы элемент вихря, определенный длиной размаха. Поэтому он заменил крыло присоединенным вихрем; "присоединенный" означает, что он не может свободно плыть в воздухе, как клуб дыма, но перемещается вместе с крылом. Его сердцевину составляет само крыло. Однако в соответствии с теоремой Гельмгольца, вихрь не может начинаться или заканчиваться в воздухе: он должен заканчиваться на стенке или образовать замкнутый контур. Поэтому Ланчестер пришел к выводу, что если присоединенный вихрь заканчивается на конце крыла, то там должно быть некоторое продолжение, и это продолжение должно быть свободным вихрем, "свободным", потому что он больше не ограничен крылом. Поэтому крыло можно заменить системой вихрей, состоящей из присоединенного вихря, который перемещается с крылом, и свободных вихрей, возникающих на концах крыла и расширяющихся по потоку. Ланчестер осознал этот основной факт в виде, как показано на его зарисовке системы вихрей, воспроизведенной на рис. 11 [1, с. 56].

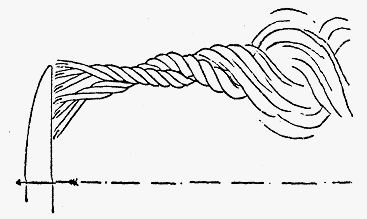
Рис. 11. Представление Ланчестером системы вихрей вокруг крыла

Впрочем, первенство Ланчестера мог бы оспорить русский инженер-теоретик Николай Егорович Жуковский. В период между 1902 и 1909 гг., независимо от Ланчестера, он разработал теорию подъемной силы.

Жуковский доказал, что если цилиндрическое тело с произвольным поперечным сечением двигается со скоростью U в жидкости, плотность которой ρ, и вокруг него существует циркуляция величиной Г, то создается сила, равная произведению ρUГ на единицу длины цилиндра. Направление силы перпендикулярно как скорости U, так и оси цилиндра.

Таким образом, мы можем объяснить явление подъемной силы, если вокруг тела действительно существует циркуляция. Для читателя, которому нравится мыслить математическими или геометрическими терминами, отмечу, что он может обобщить определение циркуляции, взяв среднее значение касательной составляющей скорости вдоль произвольной замкнутой кривой, окружающей тело, и умножив его на длину дуги этой кривой. Если течение безвихревое, то это произведение имеет одинаковое значение, независимое от выбора кривой. Таким образом, мы имеем общее определение циркуляции, обобщенное на основе циркуляционного течения с круговыми линиями тока. Если мы возьмем замкнутую кривую, которая не охватывает тело, но окружает только жидкость, то циркуляция вокруг кривой будет равна нулю [1, с. 48].

Статью не закончил; см. также смежные по содержанию статьи:

• З. Цейтлин. Вихревая теория материи, ее развитие и значение
• З. Цейтлин. Вихревая теория электромагнитного движения — 235
• В. Кельвин. О вихревых атомах
• Н.Е. Жуковский. Основы теории вихрей
• Космические вихри (Эфир, часть 5)
• Правило буравчика, гексагон Сатурна и черные дыры (КП 26)

---

1. Карман, Т. фон. Аэродинамика. Избранные темы в их историческом развитии. — Ижевск, 2001.
2. Лебединский А.В., Франкфурт У.И., Френк А.М. Гельмгольц (1821 – 1894). — М.: Наука, 1966.