
Эстетическая геометрия Револьта Пименова
Олег Акимов
Заслуга автора изящной геометрии состоит в том, что он разработал вполне оригинальную конструктивную теорию, основанную на базе окружностей и сфер с опорой на симметричные, групповые и фрактальные преобразования. Им были указаны правила построения эстетически привлекательных конструкций и доказано немало строгих теорем. Его теоретические разработки и компьютерные программы могут быть с успехом использованы для обучения учащихся и студентов специальным разделам математических дисциплин, тесно связанных с компьютерной графикой, программированием и дизайном. Проделанная Револьтом Пименовым работа, несомненно, имеет важное прикладное значение. Она выполнена на хорошем методическом и дидактическом уровне. Рекомендую, Олег Акимов.
Прошу прощения у Револьта Пименова за свое верхоглядство, что у других сурово осуждаю. Уберег я себя от соблазна воспользоваться пакетом прикладных программ DodecaTeach для построения чудных по красоте узоров. Знаю по опыту, занятие это очень увлекательное; может затянуть так, что напрочь забудешь о семье и работе. Оставим это удовольствие молодым. Свою задачу я вижу в том, чтобы сообщить народу-населению планеты, что в славном городе Питере живет славный математик, занимающийся особой разновидностью геометрии, которая называется эстетическая. Трудится он в близком мне конструктивном духе, так что моё искреннее желание популяризовать его учение понятно. Но к этой очевидной просветительской задаче хочу добавить еще одну, решение которой не столь очевидно. Сначала скажу несколько слов об основном термине.
Думаю, в предикат эстетическая Пименов вкладывает обыкновенный житейский смысл. Он хочет рассказать нам о прекрасных, если угодно, изящных или просто симпатичных геометрических конструкциях, которые радуют глаз. Но вот незадача: понятие красоты, как и понятия доброты или полезности, — субъективно, а ведь математика — штука сугубо объективная. Что ж получается? Исчез человек — и нет никакой красивой математики, поскольку этой красотой некому будет любоваться. Для кого эта красота — для Господа Бога? Здесь получается как с бензопилой: она полезна человеку, но ее полезность для ежа — сомнительна, а для Бога — тем более.
До сих пор я отказывал красоте в объективности, то есть в праве реального существования. Не так давно я беспощадно критиковал золотоискателей и гармонистов в лице Стахова, Сороко, Боднара и Семашко, а так же их критиков за неполноту уже их критики; здесь я имею в виду Белянина, Василенко и Радзюкевича. Придерживался того, характерного для меня скептического взгляда, что в архитектуре, например, божественная пропорция, во-первых, используется сравнительно редко, во-вторых, если даже детали какого-либо строения соотносятся в указанной пропорции, большого изящества она ему не придает.
Но вот открываем опус Пименова «Эстетическая геометрия или теория симметрий», который сходу начинается с золотого сечения. От него автор переходит к замечательному треугольнику, звезде, иррациональным числам. Он берет как само собой разумеющееся тот непреложный факт, что золотая пропорция — это всегда красиво. То, что в ней нет ничего безобразного, поручиться можно, но связана ли она с понятием прекрасного — вещь довольно спорная.
Прежде, мне кажется, нужно разобраться с самим понятием красоты, насколько оно объективно или субъективно. До сих пор я ставил его в один ряд с понятиями полезности или доброты, поскольку все три понятия примерно равноправны и приложимы только к субъекту. Но вот задаюсь детским вопросом: зачем самцы-павлины распускают хвосты перед самками? Неужели эти примитивные создания разбираются в гармоничном переливе ярких цветов?



Возьмите оперение петухов: оно тоже выглядит намного симпатичнее оперения кур. Не только птицы, но и насекомые (бабочки), рыбы (посмотрите на самцов гуппи), млекопитающие (грива льва, рога оленя) — все они стремятся одержать победу в эстетической сфере. Даже безмозглые растения и те в период полового созревания, перед своим оплодотворением, распускают цветы объективно красивой формы и расцветки.



Убеждаю себя: здесь нет места для телеологии, т.е. для существования скрытых сил, направляющих живые существа по пути приобретения некой гармоничной формы; тем более, здесь нет откровенной теологии. Человек неверующий скажет, что в данном случае действует естественный отбор по Дарвину. Пусть так, возразит ему верующий, но ведь такой ответ не решает проблему красоты в принципе.

Действительно, проблема прекрасного заключается вовсе не в этом. Зададимся другим банальным вопросом: как из огромной массы девушек выделить самую симпатичную? Очень просто: дайте такой же огромной массе парней
возможность проголосовать. Та, что наберет больше всего очков, и будет искомой красавицей. Разве это не доказывает, что красота — вещь объективная. Есть, конечно, какие-то субъективные предпочтения, не все проголосуют за победительницу, но фактор объективности женской красоты невозможно отрицать.
Пойдем дальше и скажем больше: практически все существа так или иначе реагируют на красивость, которая почему-то для всего живого оказывается примерно одна и та же. В самом деле, разве пчелы любуются цветами и их приятными запахами не по той же самой причине, что и мы, люди?
От философов-субъективистов можно услышать, что у жабы другие представления о красоте, чем у человека. Однако в свете сказанного данный пример выглядит уже сомнительным. Скорее, вид жабы, паука, змеи и прочих тварей неприятен, поскольку сближение с ними не сулит нам ничего хорошего. Неприятные запахи, испускаемые, например, клопами и особенно скунсами невозможно терпеть. Неприятные запахи, призваны отпугнуть тех, кто для клопа или скунса представляет угрозу.



Кажется, всё говорит нам о том, что прекрасное, как и безобразное, содержит изрядную долю объективности, не зависящую от восприятия отдельно взятого субъекта. Но в чём конкретно заключено прекрасное? Хорошо бы указать объективный критерий оценки красоты.
Мне кажется, что данную проблему можно было бы легко решить, если допустить существование Бога или другой Высшей Силы, которая, как учат проповедники, создала весь окружающий нас мир самым прекрасным образом. Но мне, беспросветному атеисту, трудно поверить в существование светлого трансцендентного существа. Это неверие в Верховную Личность, Космический Разум, гегелевский Абсолютный дух — не важно, как назвать эту могущественную энергию — сидит во мне настолько глубоко и прочно, что никакой проповедник, будь он самим Иисусом Христом, не выбьет из меня этот тотальный скептицизм.


Я уже было потерял надежду отыскать мерило объективного прекрасного, как вдруг на помощь мне приходит религиозный человек, Револьт Пименов, и говорит: я решил твою проблему прекрасного без участия Высшего Разума. Чем привлекают нас превосходные формы? Своей правильностью, — не так ли? — что на языке математики выражается симметричными групповыми и фрактальными преобразованиями сфер и окружностей.
Превосходное решение. В самом деле, не Господь Бог управляет законами филлотаксиса; не он расположил семечки в корзинке подсолнуха в соответствии с числами Фибоначчи. Здесь действуют примерно те же естественные, самоорганизующиеся силы, которые заставляют элементарные ячейки алмаза кристаллизоваться в тетраэдры, а ячейки поваренной соли — в кубы.

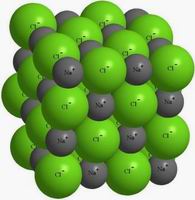

Итак, красота — это симметрия. Пименов далее разъясняет: в однообразном плоском орнаменте ее немного, в объемном сложном фрактале, построенном из сфер ее намного больше. Почему именно сфер и окружностей в плоском случае, а не точками, линиями и плоскостями? Потому, разъясняет Пименов, что точка и линия это два предельных случая окружности. Аналогично, точка и плоскость в отношении сферы. Из этих идеалов, признанных еще античными математиками и философами, автор эстетической геометрии выводит бесконечное разнообразие красивых форм.


Хорошо, пусть так, только вот загвоздка. Как быть с эллипсом, параболой, гиперболой, улиткой Паскаля и превеликим множеством других кривых, полученных на базе уравнений высших порядков? Они что — выглядят страшными уродцами в сравнении с окружностью? Это касается плоского случая, но тот же самый вопрос можно задать в отношении пространственных поверхностей.


Итак, закралось у меня сомнение в отношении отправных принципов геометрической философии Пименова. Чувствую, что он сделал неоправданно сильный акцент на окружности и сфере, утверждая, будто только они способны создавать привлекательные конструкции.
Я довольно много занимался группами и фракталам. Ничуть не сомневаюсь, что к этим областям знаний меня влекла та же любовь к прекрасному, что и Пименова. Только ведь я не ставил окружность и сферу в качестве отправных геометрических фигур. Множество людей во всем мире занимается фрактальными построениями из чисто эстетических соображений, ничего не зная о круговом и шаровом принципе Пименова.
В Сети можно найти множество сомнительных утверждений, связанных с числами Фибоначчи и золотой пропорцией. На этом сайте мою критику золотоискателей и гармонистов читайте в разделе «Конец науки», страницы: 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | . В марте этого года (2013) я разместил в Сети фильм о числах и спиралях Фибоначчи: http://youtu.be/5RmJjxwi4Qw . В этом фильме рассказывается, что числовая последовательность Фибоначчи ничем особенным не выделяется из бесконечного множества других последовательностей, которые обладают ровно теми же свойствами, что и ряд Фибоначчи. Спираль Фибоначчи (в действительности, он не имел к ней никакого касательства), вообще, не является математическим объектом. Ни один природный объект — будь то ракушка, рога барана или спиральная галактика — даже близко не напоминает эту спираль (подробности здесь и здесь .
Задача Фибоначчи о размножении кроликов. Некто поместил пару кроликов в некоторое место, огороженное со всех сторон стенками, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения.
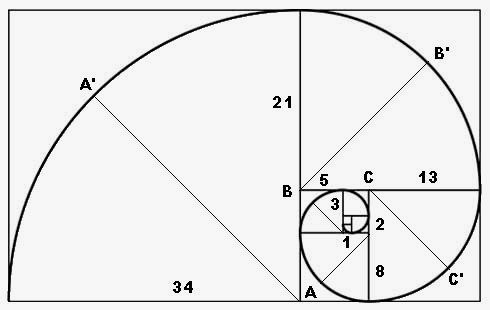
«Золотая» спираль или спираль Фибоначчи

Наутилус помпилиус (Nautilus pompilius)


Нам рассказывают, будто рога козла имеют отношение к золотому сечению
Что касается так называемого золотого сечения. С точки зрения математики, оно интересно, поскольку данная пропорция обладает многими замечательными свойствами. Когда говорят о ее "красивости" или даже "божественности", подразумевают именно эти не для всех очевидные свойства. Таким образом, дело не столько во внешней красивости золотой пропорции и чисел Фибоначчи, сколько в их особых математических свойствах.
Пропорция и числа, которых мы сейчас коснулись, известны давно. Перед ними благоговеют те, кто трепетно относятся ко всему, что связано с седой стариной. Они думают, что современные люди интеллектуально ущербны, уступают древним мудрецам в способностях, таланте и ничего толкового создать не могут. Сейчас мы покажем, что это не так.
Британия, корабельная держава, хотела знать длину береговой линии, но неожиданно натолкнулась на одну неприятную проблему. Если взять за единицу длины километр, то длина береговой линии получалась одна; если измерительным инструментом будет метровая линейка, то длина береговой линии становилась другой, во много раз большей. Вопрос: какой измерительной единицей нужно пользоваться. Ответ: все зависит от степени изрезанности береговой линии.
Данная задача породила целую область математики, связанную с фрактальной геометрией и компьютерной графикой. Ее первым исследователем был Бенуа Мандельброт, который изучал также особое множество, получившее его имя.

Бенуа Мандельброт и его множествоМножество Мандельброта не является фракталом. Его фрагменты не строго подобны исходному множеству, но при многократном увеличении определённые части графической конструкции всё больше походят друг на друга. Внутри множества Мандельброта можно выделить бесконечное количество элементарных фигур. Круг и кардиоида первыми бросаются в глаза, размеры которых постепенно уменьшается, стремясь к нулю. Каждый из этих фигур, а также овалы и завитки-спирали имеют свой набор фигур меньших размеров. На каждом последующем масштабном уровне появляются фигуры, которых не было на предыдущем уровне. Число уровней — бесконечно.
Пименов утверждает, что красота — это симметрия. Нередко в графических изображениях фракталов и множества Мандельброта строгую симметрию разглядеть не удается. Во многих случаях о ней приходится говорить как о приблизительной. Кристаллические минералы, например, уже упомянутый алмаз или даже поваренная соль, выглядят не то, чтобы красиво, но как-то интригующе и заманчиво. Не скрывается ли за этим эстетическим термином нечто иное, психологическое, а именно: любопытство узнать, что стоит за предметом, который называют красивым. Если это кристалл, интересно постичь законы его симметрии.
Пименов утверждает, что красота — это симметрия. Нередко в графических изображениях фракталов и множества Мандельброта строгую симметрию разглядеть не удается. Во многих случаях о ней приходится говорить как о приблизительной. Кристаллические минералы, например, уже упомянутый алмаз или даже поваренная соль, выглядят не то, чтобы красиво, но как-то интригующе и заманчиво. Не скрывается ли за этим эстетическим термином нечто иное, психологическое, а именно: любопытство узнать, что стоит за предметом, который называют красивым. Если это кристалл, интересно постичь законы его симметрии.
Написанный выше текст, в общем, соответствует тексту, который я произношу за кадром в получасовом видеоролике:
Из предварительного комментария
Револьт Пименов
Я представляю основы Эстетической Геометрии пьесой, где действующие лица — точки, окружности и симметрии. Начнем с простейшего. С одной окружности. Что можно сказать про главную героиню? У нее есть центр. Это как раз и не так важно. Важно, что окружность задает симметрию. Как именно — об этом будет рассказано позднее. Важно, что окружность можно поворачивать: точки или спицы на колесе меняют свое место, а само колесо остается там же. Поэтому — все точки на окружности "одинаковы".
Окружность занимает промежуточное положение между точкой и прямой. Точка — это очень маленькая окружность, а прямая — очень большая. В геометрии окружности прямая и трактуется как частный случай окружности: центр такой окружности очень (бесконечно) далек, а радиус — бесконечно велик. Иногда мы и точки рассматривает как частный случай окружностей. Окружности с нулевым радиусом. Но обычно точки все же мы отличаем от окружностей. <...>
...С помощью идей и методов, проясняющихся при изучении симметрий окружностей можно создавать изящные образы, и, идя дальше: создать среду, в которой все получающиеся образы эстетически гармоничны. Примеры можно увидеть на сайте
Симметрии относительно прямых полезны и при создании орнаментов, и при создании художественной композиции. Симметрии относительно окружности позволяют создавать значительно более разнообразные орнаменты и художественные формы, и играют существенную роль в осмыслении композиции, позволяя по-новому воспринимать плоскость и пространство. В геометрии окружности симметрия — основной способ рассуждения: чтобы доказать, что какие-то точки лежат на одной окружности, какие-то окружности касаются друг друга или пересекаются в тех же точках, что и и другие — мы доказываем, что какие-то точки и окружности симметричны друг другу. В этом — одно из резких отличий геометрии окружности и эстететической геометрии от привычной геометрии. В евклидовой геометрии симметрии определяются, но редко используются для доказательств. <…>
Никакое предварительное знакомство с математикой не требуется, а знание естественных абстракций теории групп помогает понимать работу гармонической мельницы и механизм образования фракталов. Я старался сделать текст приемлемым для гуманитариев, но и содержательным для математиков-профессионалов. <…>
Одно из лучших средств понять геометрию — рисовать чертежи самостоятельно. "Геометрия — умение хорошо мыслить по плохим чертежам" — сказано давно и очень точно. <…>
Буду рад вашим отзывам. Критическим, похвальным, любым замечаниям по теме и методу изложения. Писать можно по адресу
revoltp@mail.ru или в Живой Журнал
Я приглашаю к сотрудничеству заинтересовавшихся эстетической геометрией и ее приложениями.
Подробное изложение тем можно найти на сайте
http://revolt33.narod.ru/matem/Bereg_site/index.html
Я продолжаю публикацию работ по эстетической геометрии, смотрите статью:
Револьт Пименов
Эстетическая геометрия или теория симметрий
Оглавление и фрагменты
Часть 1. Дань прекрасной традиции.
1. Золотое сечение узла.
2. Симметрия и отклонения от нее.
3. Две красоты.
4. Формула инверсии и трудный путь через центр окружности.
5. В мире поломанных линеек: превращения окружности в прямую и точку.
6. Чертеж инверсии и А-отображения.
7. Окружности и симметрии на сфере, проекции сферы.
8. Бесконечно удаленная точка.
Часть 2. Новые методы симметрии.
9. Лепестки, обручи и биссектриса.
10. Перпендикулярные окружности. Основное свойство.
11. Симметричное симметрично симметричному.
12. Инверсия решает задачу о биссектрисах между окружностями.
13. Перпендикулярно-касательный признак и двукратное перпендикулирование.
14. Долгожданное. Две пары точек определяют симметрию. Можно начинать прямо отсюда.
15. Очень много теорем начинающихся с четырех точек на окружности.
16. Теоремы о касающихся окружностях.
17. Три точки тоже определяют симметрию.
18. Три окружности определяет симметрию.
19. Трехокружник как аналог треугольника.
20. Задача Аполлония и внутренности окружностей.
21. Моделирование геометрий трехокружником.
22. Окружность, ортогональная трем окружностям. Симметрия без неподвижных точек. Окружность не пересекается со своим образом.
23. Трехокружник из трех сокасательных окружностей. Его биссектрисы и высоты совпадают, решаем для него задачу Аполлония. Замечаем, что биссектрисы реализуют «симметрию трех точек».
24. Четыре сокасательные окружности. Великолепная шестерка точек касания, их комбинаторика. Построение из них трех перпендикулярных окружностей.
25. Биссектрисы, их свойства. как их строить.
Часть 3. В движенье мельник жизнь ведет.
26. Введение в динамический раздел. Общее понятие композиции, тождественное движение, обратное преобразование.
27. Симметричное все еще симметрично симметричному. Коммутативность, сопряженные элементы, окружность как совокупность точек и как симметрия, ассоциативность.
28. Композиции симметрий относительно перпендикулярных прямых и плоскостей.
29. Композиция симметрий относительно трех и двух перпендикулярных окружностей.
30. Биплетная симметрия, гармоническая четверка точек как часть великолепной шестерки.
31. Мельница гармонии – возведение двух лопастей. Композиции симметрий относительно двух окружностей. Пучки окружностей.
32. Исчисление симметрий, композиции симметрии относительно трех и четырех прямых, относительно двух пар окружностей точки пересечения которых сами лежат на одной окружности.
33 Симметрии в пространстве. Новые обобщения треугольника и «парапрямые».
34. Неподвижные точки. Ориентации и четность.
35. Теоремы о разбиении четверки точек на пары.
36. Теоремы о трех точках.
37. Великая барочная спираль. Компановка. решение уравнений итерациями.
38. О симметрии сфер. 4 Римановы и Лобачевские сферы – узлы и рога. Зацепления.
39. Пучки. Трехокружники из непересекающихся окружностей, о задаче Аполлония.
40. Окружность, перпендикулярная трем данным. Размножение окружностей инвертированием.
41. Немного фрактальной геометрии.Мне довелось обнаружить ряд фактов и наткнуться на новые методы, лежащие на границе разных дисциплин, и я считаю своей приятной обязанностью делиться обнаруженным.
Эстетическая геометрия неразрывно связана с геометрией окружности. Почему окружность? Потому что нет другой фигуры, создающей столь простую и столь интересную симметрию. (Предисловие)
Когда говорят про связь эстетики с геометрией и даже с математикой вообще, обычно начинают с золотого сечения. Так принято с античных времен, не нарушу традицию и я, хотя книга и посвящена совсем другим темам. (1)
Симметрия относительно прямых и точек позволяет строить орнаменты. Они интересны – особенно в их создании преуспели исламские архитекторы средних веков. Но их не так-то много и у них есть недостаток: они утомляют, орнаменты, основанные на точных симметриях предсказуемы и потому не так радуют глаз. Скорее подавляют или смиряют, чем радуют или восхищают. Итак, мы ищем то, что «симметрично, но с отклонением». На первый взгляд – задача не разрешима. Потому что не может же быть закона, позволяющего описать отклонения от закона. Отклонение от закона, от симметрии – это прихоть, произвол, вдохновение.
Есть другая симметрия, которая решает проблему. Если сравнить ее действие с симметрией относительно прямой, то, во многих случаях – они покажется нам именно «симметрией с отклонением». То, что раньше было прямым, станет немного кривым, те расстояния, которые были равны, теперь немного различаются. Все части образа чуть-чуть изменятся, но эти изменения покажутся гармоничными и согласованными. Это – симметрия относительно окружности. (2)
Есть красота двух видов. Первая знакома всем: это красота зримых образов. Ее воспевали поэты, изображали художники. Но есть и другая красота, внутренняя красота: красота поступков и красота мыслей. Есть красота математических идей и теорем: математика красива, но эта красота доступна не всем. Она подобна красоте стихотворения на редком языке: чтобы им насладиться, надо выучить язык. Математический язык, пожалуй, проще обычных языков, но мало его понимать – надо уметь следовать мыслью за рассуждением, нужно сотворческое внимание.
Эта книга названа «Эстетическая геометрия» именно потому, что изучение симметрий относительно окружности совмещает в себе оба вида красоты. Многие теоремы очень изящно и неожиданно доказываются, оказываются введением прямо в суть современной математики. Но не только внутренняя красота присуща этим теоремам – чертежи к ним часто привлекательны и могут раскрыть секреты композиции, которые настойчиво искали и находили Кандинский, Сальвадор Дали, Эшер и многие другие мастера. Правила этой геометрии позволяют строить разнообразнейшие орнаменты, фракталы, неожиданные барочные или абстрактные композиции, создавать зооморфные образы. Вероятно, биология пользуется законами симметрии относительно окружности. В физике эти законы позволяют моделировать линии силовых полей электромагнитного поля и траектории движения пары тел под действием силы тяготения. А для эстетики важно, что эти законы позволяют создать динамическую среду, где каждый шаг подчиняется гармонии. Часто это порождает завораживающие картины, что демонстрируется в программе DodecaLook.
В геометрии симметрия между окружностями называется инверсией. Она открыта Магнусом в 1831 году, ее изучали Мебиус – изобретатель полоски, у которой всего одна сторона, Софус Ли, Клейн – обобщивший одностороннюю полоску до односторонней бутылки и Пуанкаре. На Клейна геометрия окружности произвела столь большое впечатление, что он обдумывал вопрос: а не построить ли преподавание геометрии опираясь на инверсию и геометрию окружности? (3)
Обычно окружность определяют как «геометрическое место точек, равноудаленных от данной». Странно, но в эстетической геометрии мы стараемся от этого определения избавиться. Это удается – мы понимаем окружность как то, относительно чего есть симметрия.
В геометрии прямых мы не спрашиваем, что такое прямая, а пользуемся нашим умением проводить прямые через пару точек, умением откладывать прямой угол, измерять расстояния. В геометрии окружности мы попадаем в мир, где поломались линейки, но каким-то чудесным образом мы умеем проводить окружности по трем точкам (ведь через любые три точки можно провести одну и только одну окружность). Также мы умеем осуществлять симметрию относительно окружности, то есть по точке или окружности, или любой фигуре – построить точку, окружность или фигуру симметричную ей. Мы узнаем, что это умение избыточно: достаточно уметь проводить окружность по трем точкам. Но, хоть оно и избыточно – оно чрезвычайно полезно.
Такой мир, с поломанными линейками – оказывается куда разнообразней привычного нам прямолинейного мира. Потому что на самом деле прямые и точки – частные, предельные случаи окружности. Математики порой называют такие случаи «вырожденными». В самом деле, возьмем окружность и будем уменьшать и уменьшать ее радиус. Окружность становится все меньше, пока не превратится в точку. Теперь будем, наоборот, раздувать нашу окружность, делая ее радиус все больше и больше – окружность будет все более напоминать прямую, пока при очень большом радиусе – станет неотличима от нее, а при бесконечно большом радиусе – просто превратится в прямую. Это становится еще яснее, если положить окружность (колесо) на прямую. Начнем теперь увеличивать радиус колеса, так, чтобы оно все время касалось прямой. Чем больше будет колесо, тем трудней отличить его от этой прямой. В конце-концов мы увидим, что оно просто слилось с прямой (увидим, разумеется, только если мы сами не растем вместе с колесом). Мы можем мыслить иначе: не колесо увеличивается, а уменьшаемся мы сами. Тогда окружность, касающаяся прямой, покажется нам неотличимой от этой прямой. Итак, прямые – частный случай окружностей (бесконечного радиуса), а сами окружности – фигура промежуточная между точкой и прямой.
На самом-то деле у нас нет «настоящих прямых»! Это они – плод нашего ума и рук, а окружности и сферы – свойственны природе. Ведь все наши прямые мы проводим по Земле, имеющей, как известно, шаровидную форму. Поэтому наши привычные прямые, которые мы рисуем, и по которым мы движемся – кусочки окружностей очень большого радиуса (радиуса Земли). Неограниченность прямой – тоже очевидно не дана нам в опыте, кто знает, можно ли прямую «продолжать неограниченно», по крайней мере, если продолжать прямую на школьной доске, то она дойдя до стенки начнет изгибаться. (5)
...Композиция симметрий относительно пяти окружностей сводится к композиции симметрий относительно трех окружностей. Поэтому нет смысла рассматривать композицию симметрий относительно больше чем четырех окружностей – новых форм это не даст. (37) <...>
Совершим экскурсию в геометрию и симметрии сфер в трехмерном пространстве. Для эстетической геометрии это имеет большое значение. Сперва перечислим, какие симметрии есть в трехмерном пространстве. Типы симметрий окружностей стали видны из рассмотрения трех взаимноперпендикулярных окружностей. В пространстве существуют четыре взаимоперпендикулярные сферы, обозначим их А, В, С, D. Композиции симметрий относительно этих сфер и определяют типы симметрий сфер в трехмерном пространстве. Первый тип симметрии – симметрия относительно сферы, она обычно определяется аналогично тому, как определяется инверсия на плоскости относительно окружности. Например – через произведение расстояний. <...>
Второй тип симметрий понятен из рассмотрения А*В. Это – композиция симметрий относительно двух перпендикулярных сфер. При этой симметрии неподвижной остается окружность, по которой пересекаются А и В, и мы можем говорить о симметрии относительно окружности в трехмерном пространстве. Чтобы найти симметричную Х точку при такой симметрии, достаточно провести сферу, через Х и неподвижную окружность, и осуществить на этой сфере инверсию Х относительно окружности. <...>
Третий тип симметрий понятен из рассмотрения А*В*С. Это симметрия относительно пары точек пересечения сфер А, В и С, иными словами – биплетная симметрия <...>
Четвертый тип симметрий усматривается из композиции А*В*С*D. У этой симметрии нет неподвижных точек, она подобна «симметрии окружностей без неподвижных точек». При этой симметрии меняются местами все точки пересечения сфер А, В, С, D. Между описанными симметриями есть красивые взаимоотношения, подобные тем, что мы видели в симметриях, порожденных тремя ортогональными окружностями, но эти взаимоотношения более богаты, т.к. мы имеем дело с большим числом типов симметрий. <...>
Многие теоремы геометрии сфер переносятся без помех и очень изящно. Например, теорема о «серединной окружности» превращается в теорему о «серединной сфере» <...>
В связи с эстетической геометрией нас интересует композиция симметрий относительно сфер. Какие типы фигур мы можем получить благодаря ей, как двигаются точки, окружности и сферы? Прежде всего, укажем, что если такое преобразование неподвижно на четырех точках, лежащих на сфере, то это преобразование или тождественное движение, или симметрия относительно этой сферы. Доказательство аналогично рассмотрению в (). Мы заселяем эту сферы точками, полученными из исходных с помощью биплетных симметрий, и симметрий относительно окружности. Эти точки тоже должны быть неподвижны при данном преобразовании. Значит – вся сфера неподвижна при данном преобразовании. Отсюда требуемое доказывается тривиально. Точно также, симметрия относительно сферы меняет ориентацию. Поэтому композиция из нечетного числа симметрий относительно сфер не может быть тождественным движением. Кстати, в геометрии сфер ориентация появляется не у четырех, а у пяти точек.
Мы видели, что композиция симметрий относительно пяти окружностей равна композиции симметрий относительно каких-то трех окружностей. Точно также можно доказать, что композиция симметрий относительно шести сфер равна композиции симметрий относительно четырех сфер. Поэтому достаточно изучать свойства композиции относительно пяти сфер. Фигуры, получаемые в результате действия такой композиции обладают некоторой симметрией, по сути это «удвоенные» фигуры, полученные в результате композиции относительно четырех сфер. Возможно, что это «удвоение» очень существенно для биологов, художников и архитекторов, но для математики – достаточно изучать композицию симметрий относительно 4 сфер <...>.
И преобразования Римана и преобразования Лобачевского позволяют моделировать не только линии, но и поверхности, траектории «наматываются» создавая поверхности, причем поверхности эти кажутся пересекающимися, изгибающимися, напоминая в некоторых своих частях ленты Мебиуса. Получаются среди них и фигуры, напоминающие знаменитые лестницы Эшера. Разумеется, все эстетическое богатство форм появляется, когда мы рассматриваем не движение точек, а движение сфер или шаров. (см %). Неплохое представление о таких поверхностях дают раковины. Поскольку у раковин обычно есть две предельные точки: из которой раковина растет, и в которую она закручивается раковины больше связаны с преобразованием Лобачевского. Если же мы будем рассматривать более сложные раковины, то их не удастся промоделировать композициями сфер в трехмерном пространстве, они будут получаться проекцией многомерных преобразований сфер в трехмерное пространство. Или, их можно моделировать методами программы Dodeca.<...>
Очень интересны проекции возникающих фигур на плоскость. Например, мы видим, что сложные плоские орнаменты возникают как проекция трехмерных узлов. Впрочем, на это намекают и многие древние орнаменты. изображенные в виде переплетающихся линий.
Я называю формы, полученные из преобразований Лобачевского «рогами» — отчасти следуя Сальводору Дали, который писал о закрученных «носорожьих рогах» как о всеобщем принципе форм, а формы, полученные из преобразований Римана – «узловидными». Правда, эти «рога» порой сами напоминают узлы. В двумерном случае формы можно описывать используя комплексные числа и комплексную эскпоненту, изображением которой служит логарифмическая спираль. В трехмерном случае, вероятно, подойдет исчисление кватернионов и кватернионные экспоненты. Но никакое исчисление не может заменить геометрического построения форм с помощью композиции симметрий – только оно в полной мере раскрывает эстетическое значение происходящего. И для рассмотрения многих геометрически тем тоже — лучше пользоваться геометрией симметрий, а не исчислением экспонент. (38)
Скачать весь текст книги можно здесь





