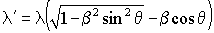Физика ХХI века:
классический ренессанс

К.П. Агафонов

Глава 3. Релятивистские эффекты
и пространство-время

Проблема релятивизма и пространства-времени
рассматривается на двух уровнях: в рамках
школьного курса физики и на базе обобщённого
уравнения Ньютона-Лоренца. Подтверждается
трёхмерная структура реального пространства-
времени, выявляется физическая природа
релятивистских эффектов, тёмной материи,
закона Хаббла и др.

3.1. Постановка задачи

Проблемы движения и пространства-времени в виртуальной физике составляют предмет исследований специальной и общей теорий относительности Эйнштейна. ОТО описывает движение в сильных гравитационных полях, вблизи массивных космических тел; СТО — в отсутствие таких полей, на достаточном удалении от их источников. Это общепринятое положение содержит противоречие, практически сводящее на нет область применения СТО, базирующейся на так называемых инерциальных системах отсчёта и преобразованиях Лоренца.

Суть его состоит в том, что в природе согласно наблюдениям существует один вид движения — вращение. Равномерное и прямолинейное движение есть предельный случай вращения, осуществляемого по траектории бесконечного радиуса. По этой причине удаление от источников силовых полей означает увеличение радиуса траектории и уменьшение скорости вращения частицы, но не трансформацию вращения в линейные перемещения частицы или связанной с ней вращающейся системы отсчёта в инерциальную. Ибо вращение всегда остаётся вращением из-за присущего ему постоянства момента импульса. Вращение при малых скоростях и больших радиусах траектории допустимо идеализировать до уровня инерциальной системы, чтобы использовать преобразования Галилея. Переход к релятивистским скоростям в таких условиях означает уменьшение радиуса траектории частицы и существенное отклонение этой траектории от прямолинейной, а связанной с частицей системы отсчёта — от инерциальной. Игнорирование этого обстоятельства, на наш взгляд, и порождает многочисленные противоречия в СТО, которым мы далее уделим должное внимание.

Согласно другим точкам зрения эти противоречия обусловлены непоследовательным построением СТО, на которое впервые обратил внимание Пуанкаре. Она выдвигает на первое место пространственно-временной аспект (релятивистскую кинематику), подчиняя ему законы движения физических объектов (релятивистскую динамику). Пуанкаре, напротив, считал первичным релятивистскую динамику и в силу этого не признавал СТО. Впоследствии Эйнштейн сам указал на недостаток принятого им построения теории. «Можно заметить, — писал он, — что теория вводит (помимо четырёхмерного пространства) два рода физических предметов…. Это в известном смысле нелогично; собственно говоря, теорию масштабов и часов следовало бы выводить из решения основного уравнения (учитывая, что эти предметы имеют атомную структуру и движутся), а не считать независимой от них» [25].

[Примечание 1. К.П. Агафонов верно подметил принципиальную разницу между ТО Эйнштейна и Пуанкаре как системами мира кинематической (Птолемеевской) и динамической (Ньютоновской). Об этом подробно рассказывается на странице Теория относительности Пуанкаре. Оба варианта релятивистских теорий ошибочны, но эйнштейновский намного хуже. — О.Е. Акимов

Комментарий автора. Я не историк физики и не математик, а инженер. Моя работа, в первую очередь, предназначена для инженеров и изобретателей. По этой причине задача критики релятивизма вообще мною не ставилась. — К.П. Агафонов].

Таким образом, задача состоит в том, чтобы построить самосогласованную релятивистскую теорию движения применительно к вращающимся объектам без использования инерциальных систем отсчёта и преобразований Лоренца. Только в этом случае область применения её становится практически значимой. А для этого, в свою очередь, свободную материальную частицу следует наделить природной способностью к самовращению. Вопрос в том, как обосновать такую способность — естественное движение «небесного вещества» по Аристотелю, — не входя в противоречие с принципом инерции.

Здесь возможны варианты. Можно обратиться к мировому эфиру или физическому вакууму, наделив их соответствующими свойствами и взяв за аналог сложное вращательно-поступательное движение заряда в магнитном поле. А можно сохранить классическое понятие вакуума как абсолютной пустоты, но распространить такое движение на случай взаимодействия свободной частицы с собственным силовым полем (неоклассическая концепция). Тогда, в частности, различие между движением электрона в сильном магнитном поле и в пустоте при взаимодействии с относительно слабым собственным магнитным полем следует признать чисто количественным. В главе 1 мы отдали предпочтение последнему варианту по той простой причине, что он не требует введения дополнительных гипотез. Напротив, вместе с инерциальными системами отсчёта оказываются невостребованными оба постулата СТО и вся теория радикально упрощается и обогащается новыми результатами. Важнейшими из них являются подтверждение трёхмерной структуры пространства-времени, обоснование космологической гипотезы Большого взрыва, обоснование причин ускоренного разбегания удалённых галактик и обнаружение так называемой скрытой массы силового поля. Последнее обстоятельство удачно разрешает наиболее актуальную проблему современной теоретической и экспериментальной космологии: выявление физической природы так называемой «тёмной материи».

3.2. Если бы Эйнштейн …

Один из наших популярных юмористов подметил: «Есть понятия умный и разумный. Это разные понятия. Умный — это человек, который много знает, разумный — который понимает (разумеет) то, что знает. К сожалению, большинство современных учёных — люди исключительно умные. Ибо являют собой не редкий подарок Природы, а массовый продукт образовательного конвейера». И в этом, по-видимому, разгадка долголетия СТО Эйнштейна, уже отметившей 100-летний юбилей.

Если бы Эйнштейн более глубоко, до понимания усвоил начальный курс классической физики, он бы повёл себя разумно и не решился посягнуть на абсолютные пространство и время Ньютона созданием специальной теории относительности. Ибо последняя оперирует инерциальными системами отсчёта (ИСО), которые привязываются к телам, движущимся по инерции равномерно и прямолинейно; а такое движение подробно изучается уже в начале школьного курса физики.

И каждый школьник знает: когда он едет в автобусе, который обгоняется мотоциклистом, то кажущаяся из автобуса скорость мотоциклиста меньше действительной на величину скорости автобуса; и наоборот, кажущаяся из автобуса скорость встречного мотоциклиста всегда больше его действительной скорости. При этом действительная скорость мотоциклиста может быть подсчитана путём векторного сложения скорости автобуса и кажущейся или относительной скорости мотоциклиста (преобразования Галилея).

Постулат Эйнштейна с = const. Успевающему школьнику может быть предложена для решения такая задача. Согласно измерениям и СТО Эйнштейна распространение светового луча, в отличие от движения мотоциклиста, указанному закону сложения скоростей не подчиняется. При этом измеряемая из автобуса скорость света одинакова как для встречного луча, так и для обгоняющего, и не зависит от того, движется автобус с наблюдателем или стоит на месте. Объяснить причину наблюдаемого парадокса.

Первое, что сделает школьник — это представит последний случай в следующей математической форме:

с = l₀ / t₀ = l / t = const;       (3.1)

здесь l₀ и t₀ — пробегающий лучом света путь и затраченное на это время, измеренные наблюдателем из стоящего автобуса, l и t — те же параметры, измеренные наблюдателем при движении автобуса.

Далее, глядя на своё произведение (3.1) и подумав, наш герой сообразит, что причина парадокса обусловлена необычным поведением измеряемых параметров пространства и времени, стоящих в числителе и знаменателе дроби (3.1).

«Совершенно верно, — одобрит учитель. — Согласно СТО Эйнштейна это явление, названное релятивистскими эффектами, объясняется относительным характером пространства и времени, обусловленного их кинематическим деформированием при высоких скоростях наблюдателя. В этой теории используется следующая терминология, которой будем придерживаться и мы:

– соотношение (3.1) определяется как второй постулат СТО;

– l₀ и t₀ — параметры абсолютного ньютоновского или классического пространства и времени, т. е. не изменяющиеся их эталоны;

– l и t — параметры эйнштейновского относительного или релятивистского пространства и времени, изменяющиеся при переходе от одной ИСО к другой.

Продолжим. Согласно СТО наблюдаемые из движущегося автобуса релятивистские расстояния или длины предметов l сокращаются в направлении движения тем в большей мере, чем выше скорость наблюдателя. Что происходит в этом случае с наблюдаемыми из автобуса релятивистскими часами?»

«Время по таким часам также должно сократиться» — уверенно ответит школьник. «Возможны ли другие решения?» — спросит учитель.

«Возможны» — ответит ученик. И обратит внимание учителя, что представленное выше математическое определение скорости света (3.1) справедливо и в рамках ньютоновской концепции абсолютных пространства l₀ и времени t₀. Ибо требование здесь одно: числитель и знаменатель дроби (3.1) обязаны либо сохраняться неизменными, либо изменяться по одному и тому же закону.

«А согласно Эйнштейну, — вмешивается учитель, — параметры наблюдаемого из движущегося автобуса релятивистского пространства и времени определяются следующими, совершенно разными законами:

l = l₀ (1 – u²/c²)^½       (3.2)

t = t₀ (1 – u²/c²)^{– ½}       (3.3)

— сокращение (сжатие) релятивистских длин l при повышении относительной скорости наблюдателя сопровождается замедлением (удлинением, растяжением) релятивистского времени t. Что ты на это скажешь?»

Парадокс движения. «Соотношения Эйнштейна (3.2) и (3.3) не верны, — поразмыслив, сделает вывод школьник, — и вот почему. Насколько мне известно, по своему замыслу СТО — это релятивистская теория движения, и как таковая она способна только уточнить результаты классической теории движения при выходе за границы применимости последней, но не ставить эти результаты «с ног на голову». А формулы СТО о сокращении релятивистских длин (3.2) и замедлении релятивистского времени (3.3) мною воспринимаются буквально и однозначно: в области релятивистских скоростей по неведомым причинам для прохождения меньших расстояний требуется большее время. Очевидно, что этот вывод не только противоречит тривиальному житейскому опыту, но и ведёт к следующему абсурдному утверждению: с повышением скорости движения тела она фактически уменьшается.

В самом деле, при движении объекта с релятивистской скоростью u₁ наблюдаемые из него релятивистские пространство и время характеризуются величинами

l₁ = l₀ (1 – u²₁/c²)^½

t₁ = t₀(1 – u²₁/c²)^{– ½}

При движении с релятивистской скоростью u₂ > u₁ соответственно имеем:

l₂ = l₀ (1 – u²₂/c²)^½

t₂ = t₀(1 – u²₂/c²)^{– ½}

При этом получаем:

l₂ < l₁ (релятивистское пространство сократилось).

t₂ > t₁ (релятивистское время увеличилось).

Таким образом, во втором случае, т.е. при возросшей фактической или классической скорости движения наблюдателя меньшее расстояние l₂ пройдено им за больший отрезок времени t₂ и, следовательно, с меньшей релятивистской скоростью. В предельном же случае движения, при u = c (фотон) эти соотношения дают результат c = 0, грубо противоречащий и опыту, и самому исходному постулату (3.1)».

«Смело, но убедительно, — делает вывод учитель. — В изложенном вся суть теории относительности — как частной, так и общей: чем больше мы увеличиваем скорость движения в рамках "классики", тем меньшей она оказывается с позиций ТО. В частности, согласно "классике" тело, падающее на "чёрную дыру" (о них я вам кое-что рассказывал) при достижении горизонта событий приобретает скорость, равную скорости света, а согласно ТО такое падение вообще прекращается. Как будто со стороны "чёрной дыры" вдруг возникла неведомая сила отталкивания, которая в последний момент остановила падение тела, в точности уравновесив силу гравитационного притяжения.

Рис. 3.1.
Характер изменения скорости тела:
1 - согласно классической механике;
2 - согласно СТО Эйнштейна

На основании соотношений (3.2) и (3.3) можно построить и соответствующий график (кривая 2 на рис. 3.1) зависимости релятивистской скорости движения u' = l / t, предсказываемой СТО, от истиной или классической скорости объекта u = l₀/t₀. График функции, построенный по соотношению u'/u = 1 – u²/c², в диапазоне значений u'/u = 0 ... 1, показывает, что даже при малых скоростях движения релятивистская и классическая механика (прямая 1 на рисунке) дают существенно расходящийся результат; а при больших, сопоставимых со скоростью света, обнаруживается их полное расхождение. А именно: в предельном случае u/c = 1 классическая механика даёт скорость, равную скорости света, а релятивистская механика Эйнштейна даёт нуль».

«И причина парадокса движения, — продолжает ученик — предельно ясна: соотношения (3.2) и (3.3) не удовлетворяют сформулированному выше необходимому условию идентичности законов релятивистского деформирования пространства и времени. Математически это требование в данном случае должно выглядеть так:

l/l₀ = t/t₀ = f(u/c),       (3.4)

где f (u/c) — одна из двух функций, входящих в соотношения (3.2) и (3.3). Но какая?»

[Примечание 2. Вывод, сделанный из диалога между учителем и учеником правильный, однако лежит он в плоскости ТО Эйнштейна. Через этот диалог К.П. Агафонов показал внутреннюю противоречивость эйнштейновского варианта ТО. Но мы можем заметить, что, например, в курсе теоретической физики Ландау и Лифшица соотношение (3.3) записано иначе, а именно: аналогично соотношению (3.2), т.е. в принятых здесь обозначениях эталоны длины и времени в учебнике [27, с. 20 – 24] меняются однотипно:

l = l₀ (1 – u²/c²)^½ ,       (3.2)

t = t₀ (1 – u²/c²)^½ .       (3.3')

Казалось бы, Ландау и Лифшиц исправили ошибку, допущенную Эйнштейном. Однако после внимательного изучения данного вопроса в ТО был обнаружен парадокс штриха, заключающийся в том, что при условии движения «штрихованной» координатной системы (K') и находящейся в покое «нештрихованной» системы (K) в принципе невозможно сказать, какой из вариантов правильный. Помимо двух уже названных вариантов право на существование имеют еще два:

l = l₀ (1 – u²/c²)^{– ½} ,       (3.2')

t = t₀ (1 – u²/c²)^½       (3.3')

— этот вариант изменения эталонов длины и времени представлен в известном «Берклеевский курс» (Механика (БКФ). Т.1. Ч. Киттель, У. Найт, М. Рудерман. — М., 1971, с. 373 – 377);

l = l₀ (1 – u²/c²)^{– ½}       (3.2')

t = t₀ (1 – u²/c²)^{– ½}       (3.3)

— этот вариант представлен в не менее известном курсе Левича (Левич В.Г. Курс теоретической физики. Т.1. – М.: Физматгиз, 1962, с. 200 – 203); О проблемах, связанных с парадоксом штриха, рассказывается на следующих страницах:

Парадокс штриха для координат ,
Парадокс штриха и парадокс лыжников ,
Парадокс штриха (слайд № 5) ,

На этих страницах раскрываются и причины возникновения парадокса штриха. В итоге получается, что существующее в рамках ТО противоречие в формулах изменения длины и времени указывает на их ненужность для теории. Об этих формулах релятивисты много говорят, но фактически они ими не пользуются. Создается впечатление, что изменение масштабов является фикцией, умственным наваждением, реально же его никто не наблюдал.

После тщательного изучения диаграммы Минковского обнаружилось, что получение формул (3.2), (3.3) и (3.2'), (3.3') из преобразований Лоренца делается с грубейшими математическими ошибками. В частности, для диаграммы Минковского, показанной ниже на рисунке, в точности выполняются следующие преобразования:

  и      

Эти преобразования можно превратить в преобразования Лоренца путем изменения масштабных единиц штрихованной системы и введения масштабного коэффициента k_n :

= ,

= .

где , — нормированные координаты,

— нормировочный, или масштабный, коэффициент.

Таким образом, между «эталонами длины и времени» (релятивистский термин, лучше сказать масштабными единицами) системы K и K' выполняются неравенства: Δx > Δx'_n и Δt > Δt'_n , т.е. происходит «сжатия» обеих штрихованных осей, так как масштабный коэффициент k_n < 1. Об ошибках получения формул для масштабов осей штрихованной системы подробно говорится на страницах:

Масштаб осей при гиперболическом повороте ,
Ортогональные и гиперболические преобразования ,
Радиолокационный метод ,
Математические ошибки ТО (слайд № 7) ,

Однако превращение исходных преобразований, соответствующих диаграмме Минковского, в преобразования Лоренца путем умножения числителя и знаменателя на релятивистскую величину есть прием искусственный. В действительности, никакого сокращения нет. О нем заговорили после неправильно истолкованного эксперимента Майкельсона – Морли, который разбирается на страницах:

Эксперимент Майкельсона – Морли ,
Спекуляции ТО (слайд № 8) .

Парадокс штриха не ограничивается изменениями пространственной и временной осей. Он простирается и на формулы для релятивистского эффекта Доплера, где его роль особенно разрушительна, так что он превращает ТО в полное ничто. Дело в том, что в отсутствии мировой среды (эфира) и действия релятивистского принципа относительности возникает принципиальная неопределенность в выборе формулы для движущегося источника и приемника. Релятивисты рассматривают только относительную скорость v, которая составляется из разности двух скоростей: скорости приемника v₁ и скорости источника v₂. Если приемник покоится, а источник движется, то длина волны, согласно принятой сегодня теории, определяется выражением:

если источник покоится, а приемник движется, будем иметь:

Теперь представьте себе, что среда отсутствует, нет отдельно скорости v₁ и отдельно скорости v₂, но есть некая относительная скорость v = v₁ – v₂. У нас тут же возникнут проблемы: мы не будем знать, какой из двух только что выписанных формул необходимо воспользоваться. Нетрудно догадаться, что никакого критерия выбора между двумя вариантами формул у сторонников тотального принципа относительности не существует. Формулы выводились из физики волновых процессов, протекающих именно в среде, которая и вносит в формулы элемент абсолютности. Можно ожидать, что в книгах по релятивистской физике числитель и знаменатель математических выражений, описывающих эффект Доплера, будет произвольным образом меняться местами, так как без среды авторы не в состоянии определиться с конкретным видом формулы.

Так оно и оказалось. Если заглянуть в «Справочник по физике» Б. М. Яворского и А.А. Детлафа, в «Оптику» Д. В. Сивухина, «Общую физику» Ж. Росселя и в «Оптику движущихся тел» У. И. Франкфурта и А. М. Френка, то можно увидеть, какую невообразимую путаницу внесли релятивисты в этот вопрос. Отсюда немедленно возникает подозрение, что релятивистские формулы Доплера работают как-то неправильно. Так как результаты экспериментальных данных релятивисты часто сравнивают с результатами, полученными по классическим формулам Доплера, то возникают подозрения и в отношении последних. Известно, что формула

является приближенной, получена при условии малости длины волны по сравнению с расстоянием между приемником и источником. ТО — точная наука, по заверениям ее сторонников, значит, для получения релятивистских формул надо воспользоваться точными формулами классической физики. Но они никому не известны! Никто никогда не выводил формул для случая, когда источник и приемник находятся вблизи друг друга, например на расстоянии сравнимым с длиной волны.

И вот оказалось, что этой формулой является обыкновенное выражение для сложения двух векторов,

в которое не входит расстояние между источником и приемником. Другими словами, оно никак не зависит от расстояния, т.е. применимо как для малых, так и для больших расстояний.

В традиционную формулу тоже не входит эта величина, т.е. в ней отсутствует критерий для определения того, на каком расстоянии должны находиться источник и приемник, чтобы формула не давала большую погрешность. Однако традиционная формула является приближенной. В отсутствии критерия радиуса ее действия возникает вопрос о её истинности. Результаты изучение данной темы изложены на страницах: страницах:

Лекция 4. Эффект Доплера ,
О формуле, описывающей классический эффект Доплера ,
Ошибочность релятивистской формулы Доплера ,
Квантовая теория Доплер-эффекта В.Л. Гинзбурга ,
Часто задаваемые вопросы по эффекту Доплера ,
Введение в конструктивную физику ,
Радиолокационный метод .

Подведем итог. Приводя диалог между учителем и учеником, К.П. Агафонов лишь слегка коснулся огромного пласта проблем, лежащих в самых основаниях ТО. Его критика справедлива, но далеко недостаточна. — О.Е. Акимов

Комментарий автора. И здесь Вы абсолютно правы. Замечу только, что в моей работе речь идёт о МНИМЫХ величинах релятивистских сокращений. Видимо, в силу этого «Об этих формулах релятивисты много говорят, но фактически они ими не пользуются»; а у Вас лично «создается впечатление, что изменение масштабов является фикцией, умственным наваждением, реально же его никто не наблюдал». Но в нашем случае Ваш аргумент «существующее в рамках ТО противоречие в формулах изменения длины и времени указывает на их ненужность для теории» теряет силу. Ибо комплексные числа широко используются именно в теориях.

«В действительности, никакого сокращения нет» — утверждаете Вы. А как же быть с сокращением длин волн и периодов колебаний в результате деформирования силового поля? Надеюсь, Вы их не отрицаете?

«Невообразимая путаница», которую внесли релятивисты в теорию движения, конечно же обусловлена использованием относительных систем отсчёта. Насколько я понимаю, Вы предпочитаете устранить её возвратом к гипотезе мирового эфира как абсолютной системе отсчёта. Я же такой необходимости не вижу. Ибо однажды обнаружил, что функцию такой системы с успехом выполняет уже известная связанная система отсчёта, приводящая к векторной форме решения задачи. Связав систему отсчёта с изучаемым объектом и привязав к нему известные мне внешние силы, мне далее становится «наплевать», движется этот объект (динамический режим) или покоится (статическая задача). То есть разделы физики «Статика» и «Динамика» объединяются в один общий, физика радикально упрощается и сокращается в объёме, не говоря уже об избавлении от необходимости прибегать к давно почившей гипотезе мирового эфира. — К.П. Агафонов]

Квантовая поправка. «Давайте выберем, — вмешивается учитель, — опираясь на твёрдо установленные факты. А они таковы. Согласно СТО и данным опыта энергия релятивистской частицы, в частности, движущегося в ускорителе электрона определяется соотношением

E = E₀(1 – u²/c²)^{– ½},       (3.5)

где E₀ — энергия покоящегося электрона соответственно. А в кванто вой механике (КМ) указанным величинам энергии сопоставляются кванты энергии:

E = ħω,       E₀ = ħω₀ ,       (3.6)

где ħ - постоянная Планка, ω и ω₀ — соответствующие этим энергиям частоты электрона-волны. Решая (3.5) и (3.6) совместно, для периода колебаний электрона-волны τ получим выражение

τ = τ₀(1 – u²/c²)^½       (3.7)

которое совместно с подстановкой τ = t и будем далее использовать вместо соотношения (3.3).

Согласно (3.7) при увеличении истинной или классической скорости движения наблюдателя релятивистское время t сокращается по закону сокращения релятивистского пространства l. В пользу такого выбора говорит и простая логика. Пространство и время по современным представлениям образуют единую физическую категорию пространства-времени. Ибо в реальном физическом мире не обнаружено пространства без времени и времени вне пространства. В таком случае и изменяться пространство-время не может по двум взаимоисключающим законам. В пользу нашего выбора мы приведём позже ещё одно наглядное подтверждение. А сейчас пришло время для глобальных выводов на базе соотношений (3.2) и (3.7)».

[Примечание 3. В этом пункте К.П. Агафонов верно подметил противоречия между ТО и КМ, но, как и в предыдущем случае (см.примечание 2), его критика недостаточна. Бывший директор ФИАНа и махровый релятивист, Д.В. Скобельцын, в одной из своих статей 1977 года, указал на принципиальную нестыковку ТО и КМ. В статье под названием «Парадоксы квантовой теории эффектов Вавилова – Черенкова и Доплера», в которой он критиковал В.Л. Гинзбурга за его ошибочное объяснение эффекта Черенкова (подробности см. Квантовая теория Доплер-эффекта В.Л. Гинзбурга), Скобельцын писал: «... Согласование представлений о квантовом фотоне с теорией относительности оплачивается ценой отказа от некоторых фундаментальных квантовых соотношений. Уравнение Планка — Эйнштейна E' = hν' в движущихся средах не выполняется (здесь E' — энергия цуга волн, заданная уравнением E₀ = hν₀, где E₀ и ν₀ — значения энергии и частоты данного цуга в среде неподвижной)». По этой причине ТО и КМ не могут быть объединены в одну непротиворечивую концепцию. — О.Е. Акимов

Комментарий автора. Д. В. Скобельцин, по-видимому, прав: и сегодня официальные концепции ТО и КМ «не могут быть объединены в одну непротиворечивую концепцию». Но какое отношение это имеет к неоклассической концепции, в которой они чудесным образом согласуются? — К.П. Агафонов]

Пространство и время. «Теперь всё просто, — подхватывает школьник. — Совместное решение соотношений (3.2) и (3.7) даёт следующий результат:

l/l₀ = t/t₀ = 1,       (3.8)

Из него, во-первых, следуют равенства

l = l₀ ,       t = t₀ ,

которые определяют абсолютное пространство и время Ньютона».

«Тогдачто описывают соотношения (3.2) и (3.7) сами по себе, каждое в отдельности? — спрашивает учитель. — Что это за «пространство» l и какое такое «время» t сокращаются согласно этим соотношениям?»

«Во-вторых, — прерывает школьник, — из соотношения (3.8) следует постулат (3.1) постоянства скорости света. По этой причине мы делаем вывод, что соотношения (3.2) и (3.7) определяют относительность какого-то локального «пространства» и «времени», например, освещаемого движущимся источником света (рис. 3.2). При этом параметры l и l₀ задают длину волны света, a t и t₀ период колебаний этой волны соответственно в режимах движения и покоя источника. Измеряя эти параметры, по формулам (3.2) и (3.7) можно, вопреки принципу относительности Эйнштейна, определить величину абсолютной скорости u/с движения излучателя.

Рис. 3.2.
Движущийся источник света задаёт
локальное пространство-время

На рисунке показано, что электромагнитное или световое поле, окружающее излучатель, при движении последнего деформируется: сжимается в направлении движения излучателя, демонстрируя наблюдателю 1 так называемое голубое смещение спектра излучения; и растягивается в противоположном направлении, демонстрируя наблюдателю 3 красное смещение спектра. Эти явления известны как продольный эффект Доплера. Очевидно также, что наблюдатель 2 в этом случае должен зафиксировать поперечный эффект Доплера в виде более слабого голубого смещения спектра».

«Здесь уместно заметить, — вмешивается учитель, — что СТО Эйнштейна предсказывает красное смещение спектра в качестве поперечного эффекта Доплера. Это обстоятельство лишний раз свидетельствует в пользу нашего выбора соотношения (3.7) вместо соотношения Эйнштейна (3.3)».

«Нам осталось, — завершает школьник, — перенести полученный результат на другие физические или силовые поля, в частности, на гравитационное, ещё не обнаруженное экспериментально. Как бы не изменялось это поле при взаимодействии со своим носителем — гравитационной или инертной массой, — физическое пространство и время сохранятся абсолютными. Другими могут оказаться только константа скорости распространения гравитационных волн и функция (3.4) деформирования такого поля. Но относительным будет только «пространство» и «время» локального гравитационного поля. И понятно почему: локальных гравитационных полей бесчисленное множество, их можно сравнивать между собой; а пространство-время одно-единственное, ни с чем не сравнимое — абсолютное».

[Примечание 4. Для правильного понимания этого пункта см. Прим. 2 и 3. — О.Е. Акимов

Комментарий автора. Без комментариев. — К.П. Агафонов]

3.3. Энергия системы частица-поле

Из уравнения (1.19) имеем следующее соотношение:

E = Kr = pcr₀ ,       (3.9)

где p — модуль импульса mu частицы в направлении поступательной скорости. Физически оно определяет энергию деформирования силового поля в режиме вращения частицы.

Определим теперь энергию деформирования силового поля в направлении поступательного движения частицы. Для этого умножим слагаемые уравнения (1.20), характеризующего поступательное движение частицы, на скаляр dr = cdt; при подстановке Kdr = dE = mcdu согласно (3.9) интегрирование даёт

miu du + mcdu = 0     или     muiu + mcu = const.

В результате имеем

pc + iW = E₀ ,       (3.10)

где iW = muiu — полная энергия частицы. Постоянная интегрирования

E₀ = pc = im₀c²ω₀

является мнимой величиной и задаёт внутреннюю или собственную энергию частицы, утверждая эквивалентность массы и энергии. Её величина определена для условия u = 0 при сохранении импульса частицы mu ≠ 0 = const и отвечает режиму её заторможенного состояния вдоль оси OZ (см. рис. 1.3) при одновременном вращении с предельной скоростью iu = ic. Мы будем называть его режимом относительного или динамического покоя частицы, в отличие от режима принципиально ненаблюдаемого абсолютного покоя при u = 0 и iu = 0, а массу m₀ — массой динамически покоящейся частицы или просто массой покоя частицы. Вектор E₀ обусловлен излучением частицей накопленной кинетической энергии и направлен против вектора iW, притормаживая её вращение. Слагаемые векторы уравнения (3.10) графически представлены на рис. 3.3.

Рис. 3.3.
Составляющие векторного уравнения
баланса энергии (3.10)

Для перехода от векторных величин к скалярным левую и правую части уравнения (3.10) возведём в квадрат. При учёте взаимной перпендикулярности векторов pс и iW приходим к основному уравнению релятивистской динамики СТО, устанавливающему соотношение между полной энергией частицы, энергией деформирования поля и внутренней энергией

W² = р²с² + (m₀с²)².       (3.11)

При подстановке величин

W² = E² (u/с)²       и       р²с² = E²

оно приводится к виду

E²(u/с)² – E² = (m₀с²)²

или

i²E² (1 – u²/c²) = (m₀c²)².

Извлекая далее корень квадратный из левой и правой частей последнего уравнения и избавляясь от операторов «плюс-минус» путём их сокращения, приходим к несимметричному, то есть только положительному решению для полной энергии системы частица-поле

iE = m₀c² (1 – u²/c²)^{– ½}       (3.12)

вектор iE которой совпадает по направлению с вектором поступательной скорости частицы (см. рис. 3.3). Соотношение указывает на неограниченный рост величины энергии, потребной для разгона частицы до световой скорости, наблюдаемый на практике при исследованиях на ускорителях заряженных частиц.

Для малых скоростей частицы (u << с) соотношение (3.12) может быть представлено в приближённой форме:

iE ≈ m₀c² + ½ m₀u² + ....       (3.13)

Оно показывает, что в этом режиме полная энергия системы определяется суммой внутренней и кинетической энергии частицы; энергия силового поля вследствие малых величин деформирования существенной роли не играет.

3.4. Скрытая масса силового поля

Рост энергии релятивистской частицы согласно (3.12) эквивалентен неограниченному увеличению её инертной массы по закону, открытому в СТО:

m = m₀ (1 – u²/c²)^{– ½}       (3.14)

Векторное соотношение (3.9) путём возведения левой и правой частей в квадрат с последующим извлечением квадратного корня и умножением на i приведем к следующей скалярной форме

iE = imuc       (3.15)

Решая его совместно с (3.12), получаем:

im = m₀ / (u/c)(1 – u²/c²)^½ ≈ m₀ / (u/c)       (3.16)

где приближённое равенство справедливо для режимов движения при скоростях u²/c² << 1. Таким образом, наряду с массой покоя m₀ и релятивистской массой m частицы, предсказанных СТО и связанных соотношением (3.14), в наших уравнениях обнаруживается мнимая или скрытая масса im. Это обусловлено тем, что СТО имеет дело с частицей, в то время как наша теория — с системой частица-поле, массу которой и определяет последнее соотношение.

Рис. 3.4.
Зависимость релятивистской массы частицы m/m₀
и системы частица-поле im/m₀
от скорости движения

На рис. 3.4 представлены графики зависимости релятивистской и скрытой массы от скорости движения частицы. Видно, что первая устремляется в бесконечность при u → c, в то время как вторая — как при u → c, так и при u → 0. Связь между указанными массами определяется соотношением

m = im(u/c).       (3.17)

А разность масс im и m на рис. 3.4 определяет массу силового поля. Как видим, с увеличением скорости частицы последняя непрерывно уменьшается. Этот результат, по-видимому, следует понимать так. Поле покоящейся частицы распространяется на бесконечность, поэтому обладает и бесконечной массой. Поле движущейся частицы ограничено в пространстве тем в большей мере, чем выше её скорость. При u → c масса частицы-поля уменьшается, приближаясь к массе частицы (частица «сбрасывает» поле). Результатом этого является наличие нисходящей и восходящей ветвей в зависимости инертной массы частицы-поля от скорости. Минимуму функции im(u) на рис. 3.4 отвечает точка А, в которой масса динамической системы частица-поле в два раза превышает массу m₀ покоя частицы. Это обстоятельство согласуется с экспериментальным подтверждением существования электромагнитной или полевой составляющей массы тел, в частности, электрона.

Точке A на графике отвечает некоторая равновесная скорость частицы-поля u/c ≈ 0,7, соответствующая минимуму полной энергии iE ≈ 1,4 m₀c². Указанная скорость отвечает наиболее устойчивому состоянию системы частица-поле, поэтому частицы и тела с равновесной скоростью должны преобладать в общей массе свободного космического вещества. Очевидно также, что эта скорость достаточно высока, чтобы при гравитационном захвате равновесных частиц Солнцем или другой звездой поддерживать непрерывное горение последних за счёт притока кинетической энергии. Как может происходить такой захват, будет показано в следующей главе.

3.5. Трёхмерная структура и дуализм пространства-времени

Из рис. 1.3 видно, что движение частицы-поля по инерции согласно принятой модели осуществляется в реальном трёхмерном пространстве-времени, в отличие от виртуального четырёхмерного в СТО. Причём, это пространство-время является абсолютным в том смысле, что по определению (1.16), базирующемуся на опыте, характеризуется постоянством скорости c распространения деформаций в нём. Это, в свою очередь, означает, что пространство и время как раздельные категории могут и не быть абсолютными: им не запрещено изменяться таким образом, чтобы отношение характеристик dr и dτ всегда оставалось постоянным, равным скорости света в пустоте. Покажем, что такая ситуация принципиально возможна.

В соотношении (1.17) переменные легко разделяются:

cdir = udr,

а интегрирование даёт:

cir = ur + const.

Постоянная интегрирования может быть определена из следующих соображений. При заторможенной частице (электрон) согласно рис. 1.3 вектор u = 0, а вектор ir разворачивается в направлении мгновенной скорости вращения: в этом направлении частица излучает накопленную кинетическую энергию поступательного движения, вращаясь со скоростью iu = c по окружности радиуса r. Тогда вместо последнего уравнения имеем:

cir = ur – cr.

Меняя крайние слагаемые местами, получаем:

cr = ur – cir.

А деление слагаемых на cr даёт:

1 = u/c – ir / r.

При возведении левой и правой частей в квадрат и преобразовании слагаемого –2iru / rc в выражение 2ru / irc = 0 получаем интересующее нас соотношение для характеристики пространства как самостоятельной категории,

ir = r (1 – u²/c²)^½.       (3.18)

А интегрирование определения (1.16) скорости света даёт соотношение r = cτ, подстановка которого в (3.18) приводит к выражению для характеристики времени как самостоятельной категории

τ = τ₀ (1 – u²/c²)^½.       (3.19)

Физический смысл соотношений (3.18) и (3.19) вполне очевиден: для частиц, движущихся с релятивистскими скоростями, расстояния, обусловленные собственными деформируемыми силовыми полями, сокращаются, а время преодоления этих расстояний соответственно уменьшается. На рис. 1.3 этому соответствует уменьшение шага λ = 2πir (сжатие) винтовой траектории движущейся частицы, сокращение периода iτ по закону (3.19) и увеличение частоты iω её колебаний в направлении поступательной скорости.

Рис. 3.5.
Релятивистское деформирование электрического
поля движущегося заряда согласно СТО Эйнштейна

На рис. 3.5 для сравнения дана физическая интерпретация соотношения (3.18) согласно СТО: электрическое поле движущегося заряда деформируется в направлении поступательного движения и не деформируется в других направлениях. Такая картина деформирования силового поля частицы, в отличие от принятой в нашей концепции и описанной в разделе 1.7, не согласуется с твёрдо установленным фактом скалярной природы скорости света.

Соотношения (3.18) и (3.19) являются аналогами кинематических формул (3.2) и (3.3), полученных Эйнштейном на базе математических преобразований Лоренца. На них базируется эйнштейновское представление об относительности пространства и времени как раздельных категорий (абсолютно в СТО только четырёхмерное пространство-время [16]), которые противопоставляются ньютоновской модели их абсолютного характера. В нашем случае такое противопоставление оказывается некорректным: признать пространство относительным означает отождествить его с деформируемым силовым полем.

По указанным причинам нам представляется уместным говорить о субъективности оценки событий в абсолютном пространстве-времени: в силу объективных обстоятельств, связанных с процессом измерения, каждый наблюдатель, двигаясь с определённой скоростью, вынужден оценивать события в пространстве и времени по-своему, в соответствии с характеристиками (3.18) и (3.19) релятивистского деформирования силового поля собственной системы отсчёта.

Удивительно, что подобный двойственный характер или дуализм пространства-времени оставался незамеченным для физиков длительное время, хотя следует уже из элементарного анализа определения постоянства скорости света (3.1). Как мы показали выше, уже для школьника очевидно, что оно может быть справедливым только при одном-единственном условии: когда релятивистские длины и интервалы времени изменяются по одному и тому же закону. Этому условию отвечают и ньютоновские абсолютные пространство и время, и относительные их характеристики (3.18) и (3.19) релятивистского сокращения мнимых длин и времени. Эйнштейновские характеристики относительности пространства (3.2) и времени (3.3) грубо противоречат определению (3.1). Нелишне напомнить в связи с этим, что последнее является одним из исходных постулатов СТО Эйнштейна.

Столь же очевидно, что между силовыми полями как материальными объектами и пространством существует глубокое и принципиальное различие: первые индивидуальны и бесчисленны, второе является общим и единственным. Силовые поля заполняют пространство, но не сводятся к нему. А эффект деформирования времени (3.19) или (3.3), в свою очередь, не даёт оснований для серьёзного обсуждения пресловутого парадокса близнецов: мы живём в абсолютном пространстве-времени, а разделили его на пространство и время, исходя из сугубо практических соображений.

Проблема времени в нашем случае обнаруживает одну особенность. Согласно рис. 1.3 движение физического объекта представляет собой комбинацию абсолютного вращения с действительной частотой ω в реальном времени τ и прямолинейное относительное движение при частоте iω во времени iτ, которые являются мнимыми величинами. При оценке времени жизни элементарной частицы или другого материального (биологического) объекта из двух решений, действительного и мнимого, может быть признано реализуемым только одно. Мы полагаем, что это должны быть действительные параметры. Жизнь человека, в частности, измеряется количеством циклов (лет) обращения его вместе с Землёй вокруг Солнца. Тогда проблема парадокса близнецов лишается реальной почвы.

В свете сказанного нам представляется, мягко говоря, не профессиональной укоренившаяся в учебной литературе традиция: факт увеличения времени «жизни» неустойчивых космических частиц (мю-мезонов) преподноситься в качестве экспериментального подтверждения релятивистского замедления хода времени (3.3). Ибо классическая механика давно объяснила подобные факты, увязав их с величиной полной энергии (3.12) и (3.13) частиц или тел. В частности, время «жизни» (дальнобойность) артиллерийского снаряда или ружейной пули при полёте в атмосфере оказывается тем большими, чем больше их кинетическая энергия при вылете из ствола; а время «жизни» сигнальной ракеты — тем большим, чем больший запас химической энергии содержит её заряд.

3.6. Рождение и эволюция Вселенной

«Приближённое» решение. Используем дифференциальное уравнение (1.13) свободного движения тела и рис. 1.3 для описания поведения изолированной Вселенной во времени в диапазоне скоростей u/с = 0,6...0,8, для которого параметры m и K согласно рис. 3.4 можно положить неизменными. Разделение переменных и непосредственное интегрирование уравнения позволяет получить такие зависимости:

– t/T = ln(u/с)       или       u/с = m/im = exp (– t/T),

где введено обозначение T = mс/К = imc/iK. А умножение левой и правой частей уравнения (1.13) на dr = cdt и последующее интегрирование по частям даёт:

– r/R = ln(u/с)       или       u/с = m/im = exp(– r/R),

где обозначено: R = mс²/K = imс²/iK.

Рис. 3.6.
Экспонента рождения и эволюции Вселенной

На рис. 3.6 указанные зависимости представлены на совмещённом графике, который подтверждает космологическую гипотезу Большого взрыва; правда, с одной существенной оговоркой: взорвался не физический вакуум, отягощенный антигравитационными натяжениями, а релятивистская бесконечная масса-энергия горячей или даже холодной сингулярности, происхождение которой остаётся тайной Творца.

Вывод из сказанного таков: гипотеза физического вакуума входит в неустранимое противоречие с исходным уравнением динамики (1.13). составляющим фундамент классической физики. Более того, согласно данным современной космологии Вселенная расширяется с ускорением, которое обусловлено существованием всемирного антитяготения и связывается с наличием космологической постоянной Λ в гравитационных уравнениях Эйнштейна. А это, в свою очередь, означает наличие у пространства-времени принципиально неустранимой (первородной) кривизны и следовательно изначальной массы, при наличии которой физический вакуум оказывается фактически невостребованным («лишней сущностью» согласно принципу Оккамы).

Согласно рис. 3.6 образование сингулярности при t/T = 0 или t = 0 приводит далее к непрерывному расширению её вещества по экспоненциальному закону от «нулевого» объёма (r/R = 0). При этом холодная сингулярность могла быть обусловлена столкновением «голых» (при m = im) и потому не вращающихся частиц (нейтрино?), движущихся в пространстве dx ≠ 0 без времени dt = 0 (лаборатория Создателя) с бесконечной скоростью dx/dt при бесконечной же кинетической энергии. Результатом оказывается образование суперплотного нестабильного протоядра массой m₀ (см. рис. 3.4) при бесконечной внутренней энергии связи, равной кинетической энергии столкнувшихся частиц. А вся последующая эволюция Вселенной сводится к наблюдаемым и сегодня цепным реакциям спонтанного деления и распада нестабильных ядер.

Видно также: чем старше космический объект (больше время t/T его жизни), тем большие размеры он имеет (параметр r/R) и меньше скорость u/c его свободного движения; чем меньше объект, тем больше скорость его движения и меньше время жизни. На рис. 3.4 это выражается в том, что для «тихоходных» и следовательно масштабных космических объектов, таких как галактики и их скопления, «тёмная материя» заметно превалирует над веществом (левая ветвь кривой im/m₀). Такая закономерность подтверждается и данными наблюдательной астрономии: «Чем больше масштаб структуры, тем большую роль играет «тёмная материя»: в самых больших структурах — в сверхскоплениях галактик — обычное вещество есть лишь слегка заметная (по массе) компонента, распыленная по громадному облаку материи неизвестной природы» [5].

Новая концепция решает и одну из главных проблем, поставленных, но не решённых в космологической теории А. Фридмана: почему наша Вселенная расширяется в соответствии с линейным законом Хаббла

u = Hl;       (3.20)

в этом простом соотношении u — скорость наблюдаемого далёкого объекта (например, галактики или квазара), H = 65 ± 10 км/c × Мпк — постоянная Хаббла, l — расстояние до наблюдаемого объекта, а время t = l/H = 14 – 20 млрд лет используется в научной литературе в качестве грубой оценки возраста селенной.

Для этого вернёмся к исходной модели рис. 1.3 свободного вращательно-поступательного движения тела или Вселенной массой m и акцентируем наше внимание на следующем принципиально важном обстоятельстве. Как мы видели, вращение свободного тела со скоростью iu согласно рис. 1.3, а приводит к возникновению радиальной вращающейся силы [i K, iu/c], обусловленной упругими свойствами K поля. Эта сила уравновешивает радиальную составляющую силы инерции, связанную с наличием центростремительного ускорения тела, в соответствии с уравнением баланса сил (1.18). А из рис. 1.3, б следует, что поступательное движение тела порождает круговую циркуляцию силового вектора [u/c, K], который уравновешивает силу инерции тела в направлении касательной к окружности вращения в соответствии с уравнением баланса сил (1.20).

Таким образом, на свободное самовращающееся тело или систему тел постоянно воздействуют две пары противоположно направленных сил, которые создают в нём напряжения растяжения. Тогда становятся очевидными как природа формирования колец вокруг Сатурна, так и происхождение пояса астероидов в Солнечной системе. А для Вселенной в целом, вращающейся по радиусу r >> l наличие таких сил означает непрерывное увеличение её размеров. При этом первое из названных выше уравнений баланса сил легко приводится к виду

u = (K/mc)r,       (3.21)

совпадающему с законом Хаббла (3.20); второе же даёт результат du/dt = (K/mc)iu, объясняющий наблюдаемое разбегание далёких галактик Вселенной с ускорением без привлечения гипотезы космического вакуума и антигравитации или тёмной энергии. А вкупе с «расползанием» вещества космических объектов со временем it в направлении поступательной скорости согласно модели рис. 1.3 это объясняет явление, впервые обнаруженное Я. Б. Зельдовичем: масштабные космические образования не обладают сферической формой, а представляют собой «блинные» структуры с тремя неравными поперечными размерами. При учёте определения u = [r, ω] из соотношения (3.21) имеем

K = mcω,       (3.22)

где ω — угловая частота вращения. Тогда постоянная Хаббла в соотношении (3.20) приводится к виду

H = K/mc = ω

и обретает ясное физическое содержание: она характеризует угловую частоту вращения расширяющейся Вселенной в целом.

Точное решение. Чтобы избавиться от ограничений, связанных с изменением параметров m и K в исходном уравнении (1.13), разделим слагаемые его на m; при учёте (1.14) или (3.21) имеем:

[u/с, uс r₀/r] + du/dt = 0       или       u²/r + du/dt = 0.

Разделение переменных и непосредственное интегрирование уравнения с использованием, на основании (1.16), подстановки dt = dr/c даёт:

с/u = ln(r/R)       или       r/R = ехр(с/u),       (3.23)

где r — физический радиус частицы, R — постоянная интегрирования, характеризующая размеры взорвавшейся Протогалактики.

Рис. 3.7.
Функция (3.23)

На рис. 3.7 функция (3.23) представлена графически. Видим, что значению r = R на графике отвечает параметр с/u = 0 или бесконечная скорость первородных частиц; причём, это только момент их столкновения, но не начало Взрыва. А значению с/u = 1 отвечает размер Протогалактики r/R = 2,718, с которого на графике рис. 3.6 ведёт отсчёт Большой взрыв и рождение Вселенной. Увеличение значения функции r/R с ростом аргумента с/u на новом графике означает, как и раньше, экспоненциальное расширение Вселенной, сопровождаемое соответствующим замедлением скорости составляющих её материальных частиц. Графики рис. 3.7 и 3.6 представляют, таким образом, один и тот же закон рождения и эволюции Вселенной, выраженный прямой, типа у = еxp (x), и обратной, типа у = еxp (–x), показательными функциями. Мы продолжим разговор на эту тему в главе 5 в рамках термодинамической модели рождения и эволюции Вселенной.

О рождении Вселенной из «Ничего». В научной литературе имеется несколько туманных вариантов физической концепции рождения Вселенной из «Ничего» без нарушения закона сохранения. В трактовке Я. Зельдовича и Л. Грищука под термином «Ничего» понимается пустое замкнутое трёхмерное пространство без частиц, которое могло выделиться как физический объект в результате некоторого катастрофического процесса. Обязательный физический вакуум в таком пространстве поневоле оказывается в резко неравновесном состоянии, что обуславливает неизбежность эволюции пустого пространства. В процессе эволюции вакуум рождает частицы, но положительная энергия частиц и вакуума точно компенсируется отрицательной энергией гравитационного поля, в результате чего суммарная энергия Вселенной в целом остаётся равной нулю. «Так без нарушения закона сохранения энергии первоначально маленькая, пустая Вселенная преобразуется в большую Вселенную, заполненную материей — частицами» [5].

«Туманом» в подобных концепциях мы называем безадресную потенциальную энергию, по воле авторов сопровождающую рождение частиц в пустоте. Согласно соотношениям (3.12) и (3.13) полная энергия свободной частицы по определению не содержит потенциальной составляющей. Последняя, как будет показано в следующей главе, появляется только в связанном состоянии изучаемой частицы с другим материальным объектом и представляет собой важную физическую характеристику — энергию связи сложной или составной, в частности, планетарной системы тел (Солнечная система, атом водорода и др.). Сопутствующую рождению отрицательную потенциальную энергию других материальных образований (упругой среды в виде эфира или физического вакуума) также трудно себе представить. По этой причине подобные концепции рождения Вселенной нам представляются чистой воды спекуляциями и серьёзного внимания не заслуживают.

[Примечание 5. Далее идет подраздел «3.7. Пример. Ошибка Эйнштейна», в котором автор еще раз убеждает читателя, что пространство и время должны меняться не по различным законам (3.2) и (3.3), а по одинаковым — (3.4). Этот вывод с точки зрения диаграммы Минковского правильный, только ошибка Эйнштейна более принципиальна. Дело в том, что масштабы пространства и времени в действительности вообще не меняются (см. Примечание 2). — О.Е. Акимов

Комментарий автора. "Дело в том, что масштабы пространства и времени в действительности вообще не меняются" — справедливо утверждаете Вы. Я бы только написал «масштабы пространства-времени как единой и абсолютной сущности". Они изменяются при искусственном разделении её на самостоятельные мнимые категории, физический смысл которых нам ещё предстоит разгадать. — К.П. Агафонов

Примечание 6. К.П. Агафонов пишет: «E₀ является мнимой величиной и задаёт внутреннюю или собственную энергию частицы, утверждая эквивалентность массы и энергии». Таким образом, под E₀ здесь понимается скалярная величина, т.е. E₀ — той же самой природы, что и масса m. Но чуть ниже читаем: «Вектор E₀ обусловлен излучением частицей накопленной кинетической энергии и направлен против вектора iW, притормаживая её вращение». Как может энергия оказаться вектором?

Комментарий автора. Из математического аппарата комплексных чисел я заимствовал исключительно геометрический смысл операции умножения вектора на мнимую единицу, чтобы получить простую в описании и наглядную модель (см. рисунок 1.3 «Физики XXI века») пространственного вращательно-поступательного движения частицы. То есть в моей модели изначально речь идёт о векторах. Вектор энергии — не моё открытие: примером может служить вектор Пойнтинга для плотности потока энергии в единицу времени. Но это не налагает запретов на мнимые скалярные величины и на мнимую единицу i как самостоятельный множитель. Следует иметь в виду так же, что все вращающиеся векторы на рис. 1.3 (а их много) по сути являются псевдовекторами (или псевдоскалярами) вследствие самокомпенсации в процессе вращения. — К.П. Агафонов.

Примечание 6 (продолжение). Непонятна также природа мнимой массы (автор называет ее также скрытой массой, а релятивисты – тёмной материей), которая фигурирует в тексте как im. Для неё записываются, например, следующие выражения:

m = im(u/c), u/с = m/im = exp (– t/T) и u/с = m/im = exp(– r/R).

Если символом i здесь обозначена мнимая единица, то приведенные формулы теряют смысл, так как выражение m/im = 1/i и неравно функциям exp (– t/T) или exp(– r/R). Если im нужно воспринимать как один символ мнимой массы, т.е. не воспринимать i как независимый множитель, то делаются бессмысленными все предыдущие выкладки, в которых фигурирует вектор iE. В частности, непонятен переход от уравнения

E²(u/с)² – E² = (m₀с²)²

к промежуточному уравнению, куда введено равенство i² = –1:

i²E² (1 – u²/c²) = (m₀c²)².

а от него к наиважнейшему уравнению (3.12):

iE = m₀c² (1 – u²/c²)^{– ½},

откуда, между прочим, вытекает векторная природы массы m₀.

Комментарий автора. Комбинацию im нужно воспринимать как один символ мнимой массы, т.е. не воспринимать i как независимый множитель. Но и последнее не запрещено. В частности, ничто не мешает мне левую и правую части любого соотношения умножить на мнимую единицу i, чтобы повернуть вектор или преобразовать скалярную и действительную величину в скалярную же мнимую. Нельзя таким образом перейти от скалярных действительных величин к комплексным. Тут Вы правы (см. ниже). — К.П. Агафонов

Примечание 6 (продолжение). В выражениях (3.13) – (3.16) символ i выступает в роли именно мнимой единицы, так что итоговое выражение (1.17) делается уже бессмысленным: m = im(u/c), равносильно: 1 = i(u/c). Это проистекает из-за некорректных действий с мнимой единицей. С помощью подобных действий можно вывести всё что угодно, например, доказать равенство отрицательной и положительной единицы:

–1 = i² = (–1)^½ (–1)^½ = [(–1)( –1)]^½ = + 1.

Такое стало возможным в силу нашего субъективного выбора знака « + » или « – » пред квадратным корнем. Вот почему в математике действительная и мнимая части комплексного числа отделены друг от друга. Отсюда невозможно получить из действительной величины некую мнимую и наоборот. — О.Е. Акимов

Комментарий автора. Выражение (3.12) и его приближённая форма (3.13) получены нами как мнимая по своей природе вектор-энергия силового поля в направлении вектора поступательной скорости u. В этом направлении излучение частицы не выделяется при торможении. Оно выделяется (или поглощается) частицей в направлении действительного вектора E₀, как это было сказано выше. А итоговое выражение (3.17) имеет простой и очевидный физический смысл: оно устанавливает количественную связь между «голой» релятивистской частицей массой m в теории Эйнштейна и неоклассическим объектом частица-поле массой im в нашей теории. Непонятно, что здесь непонятно.

Описанная между выражениями (3.14) и (3.15) операция «Ы» с возведением в квадрат и извлечением корня квадратного, конечно же, не делает мне чести. Предлагаю заменить этот абзац на следующий: «Векторное равенство (3.9) предполагает идентичность направлений векторов левой и правой частей, а также равенство их модулей. Последнее обстоятельство позволяет переписать его в следующей скалярной форме, полученной путём умножения модулей на i».

Под влиянием Ваших примечаний раздел 3.3 и другие мной вновь внимательнейшим образом анализируются, так что не исключены дальнейшие поправки. Одна из них уже определилась, это следующий новый комментарий к соотношению (3.10) и рис. 3.3:

«Постоянная интегрирования

E₀ = pc = im₀c²ω₀

формально определяется действительной величиной и задаёт внутреннюю или собственную энергию частицы, утверждая её эквивалентность некой мнимой покоящейся массе im₀, о которой мы поговорим в следующем разделе. Направление вектора энергии E₀ задаётся вектором импульса p, а величина определена для условия u = 0 при сохранении импульса частицы mu ≠ 0 = const и отвечает режиму её заторможенного состояния вдоль оси OZ (см. рис. 1.3) при одновременном вращении с предельной скоростью iu, модуль которой iu = ic. Мы будем называть его режимом относительного или динамического покоя частицы, в отличие от режима принципиально ненаблюдаемого абсолютного покоя при u = 0 и iu = 0, а массу im₀ — массой динамически покоящейся частицы-поля или просто массой покоя. Вектор iE₀ (см. рис. 3.3) обуславливает излучение частицей накопленной кинетической энергии (мнимой массы) и направлен вдоль вектора iW, замедляя её вращение в режиме тормозного излучения (см. раздел 6.2)». — К.П. Агафонов

Примечание 7. Ссылка на главный рисунок теории К.П. Агафонов (рис. 1.3) и фундаментальное уравнение (1.13), введение в оборот терминов «псевдовектор» и «псевдоскаляр», а также некорректность использования операций с мнимой единицей заставляет нас перенестись в первую главу книги «Физика ХХI века: классический ренессанс». Продолжение диалога, начатого в примечании 6, читайте в конце пункта 1.7 первой главы Законы классической механики — О.Е. Акимов]

3.8. «Антиматерия» и элементарные «частицы»

В 1928 г. английский физик П. Дирак предложил релятивистское дифференциальное уравнение для волновой функции свободной частицы, на основе которого тремя годами позже предсказал существование частицы с отрицательной энергией — антиэлектрона или позитрона, возвестившего о космологической проблеме антивещества и антимиров. В его работе [2] читаем: «Вопрос об отрицательных энергиях возник из изучения движения частицы сообразно частному принципу относительности. В нерелятивистской механике энергия W частицы задаётся в функции её скорости u или же количества движения p формулой W = ½ m₀u² = p²/2m₀ , чему отвечают всегда положительные W; однако в релятивистской механике требуется заменить эти формулы на

W² = c²(m²c² + p²),         (3.27)

к которому в учебной литературе чаще приходят, используя следующую простую схему.

Принцип наименьшего действия позволяет получить два релятивистских соотношения, определяющих положительные величины энергии и импульса материальной частицы:

W = mc²(1– u²/c²)^–½,

p = mu(1– u²/c²)^–½.

W²/c² = m²c²(1– u²/c²)^–1,       p² = m²u²(1– u²/c²)^–1.

Вычитая почленно полученные равенства, имеем:

W²/c² – p² = m²c²,

откуда

W = ± c(p² + m²c²)^½.         (3.28)

Вот так, с помощью элементарной математики, частица с положительной энергией обретает своего «двойника» — античастицу с отрицательной энергией. А можно, используя этот приём, ещё более упростить процесс математического или виртуального рождения античастиц: не привлекая релятивистское соотношение для импульса, возвести в квадрат непосредственно и только положительную энергию частицы, а затем вычислить корень квадратный из полученной величины. В результате вместо одной частицы получаем дираковскую симметричную пару частица-античастица!

Подобного рода «математику», точнее антифизику даже комментировать неприлично. Мы привели её здесь, во-первых, для того, чтобы показать: любому выводу инвариантного соотношения (3.27), в том числе выводу на базе преобразований Лоренца, сопутствует операция возведения слагаемых в квадрат; во-вторых, продемонстрировать неправомерность в этом случае использования обратной операции в виде соотношения (3.28).

И без неуклюжей математики ясно: следов серьёзной физики в понятии отрицательной энергии не обнаруживается. Если рождённые физическим вакуумом электрон и позитрон определяют частицы с положительной и отрицательной энергией соответственно, то при их аннигиляции следовало бы ожидать нулевой баланс энергии, т. е. последняя должна была бы вовсе исчезнуть. Иными словами, появилась пара «частиц» из ничего, и туда же должна вернуться, чтобы не нарушать закон сохранения энергии. Ан, нет: вместо этого в процессе аннигиляции выделяется удвоенная положительная энергия в виде двух гамма квантов, суммарная энергия которых равна энергии порождающего фотона. И это прямо и недвусмысленно свидетельствует исключительно о положительной энергии обоих «частиц». Античастица — это физический нонсенс.

В пользу такого вывода говорит и современная космологическая проблема, связанная с хорошо изученным «обычным» или барионным веществом: «соответствующих античастиц, т. е. антибарионов (антипротонов, антинейтронов), позитронов в природе нет. Точнее, они присутствуют в ничтожных количествах и обязаны вторичным процессам рождения частиц и античастиц при столкновениях частиц высоких энергий, например, в космических лучах или на мощных ускорителях в лаборатории» [28].

В нашем случае основное уравнение релятивистской динамики (3.11) даёт только положительное решение (3.12) для энергии свободной частицы-поля; а гипотеза физического вакуума как материальной среды оказывается невостребованной, ибо с успехом может быть заменена концепцией силового поля физических объектов. — То есть упругой материальной средой, в которой при определённых условиях (релятивистские частицы в сильных полях) возможно временное образование полевых вихрей (квазичастиц), подобных вихревым макроскопическим образованиям в атмосфере (рис. 2.3, в).

Рис. 3.10.
Процесс образования элементарной пары
«частица-античастица» в упругом силовом поле

К такого рода микроскопическим полевым образованиям и относятся, на наш взгляд, все неустойчивые «частицы» (рис. 3.10), изучаемые в рамках физики высоких энергий или физики элементарных частиц. Если энергия частицы или фотона 1 достаточно велика (жёсткий гамма-квант), то в кулоновском поле тяжёлого ядра они в принципе могут породить любую пару полевых микровихрей 2 и 3 разнонаправленного вращения, которые в камере Вильсона идентифицируются как частица и античастица, в частности, электрон и позитрон.

В виртуальной физике подобными объектами, как известно, оперирует квантовая теория поля, представляя фотоны, электроны, позитроны и любые другие частицы в виде сгустков энергии различных силовых полей. Тогда оказывается, что предлагаемая нами физическая концепция ни только весьма прозрачно указывает на ошибочность идеи отрицательной энергии и антивещества, но и представляет не заслуживающими серьёзного к себе отношения раздел физики высоких энергий и квантовую теорию поля как таковые.

Выводы к главе 3

• Релятивистские законы движения могут быть получены, а их область применения существенно расширена при учёте взаимодействия частицы с собственным силовым полем без привлечения преобразований Лоренца и инерциальных систем отсчёта.
• Пространство-время является трёхмерным. Оно абсолютно и объективно, а его восприятие в виде раздельных категорий пространства и времени осуществляется каждым конкретным наблюдателем через собственное деформируемое силовое поле и является субъективным.
• Силовые или физические поля обладают скрытой массой, формируя в космосе «тёмную материю» и неся ответственность за образование в ускорителях неустойчивых полевых микровихрей, именуемых элементарными парами «частица-античастица».
• Гипотеза Большого взрыва и закон Хаббла находят строгое теоретическое обоснование в рамках неоклассической физической концепции.
• Ускоренное разбегание удалённых галактик может быть объяснено упругими свойствами космических силовых полей без привлечения гипотезы тёмной энергии.

Литература