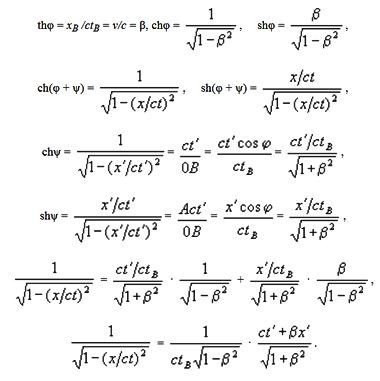Эфир (Часть 8) Мир — трехмерен:
многомерные миры не существуютО.Е. Акимов

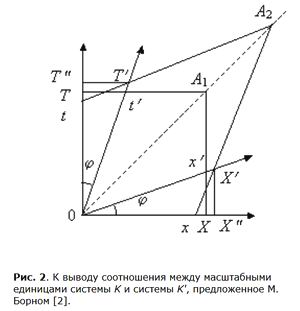
Если вы школьный учитель или вузовский преподаватель, у которого в программе стоит тема "Теория относительности", попробуйте построить одно практическое задание следующим образом. Попросите учащихся или студентов вычертить диаграмму Минковского и определить по ней реальный масштабный коэффициент сокращения длины и времени. Здесь имеется проблема, которой мы касались 6-й части видеофильма "Эфир". Напомним, в чём она заключается.

Здесь имеется проблема...Принято считать, что единицы длины и времени в движущейся системе координат K' сокращаются в соответствии с известным релятивистским множителем — корень квадратный из 1 – β² , где β = v/c — это отношение скорости движения системы K' относительно покоящейся системы K (скорость v) к скорости света c. В этом случае эталоны движущейся системы K' — Δx' и Δt' — получаются путем умножения эталонов покоящейся системы K — Δx и Δt — на указанный радикал.

Парадокс штрихаНо в 6-й части мы рассказали о парадоксе штриха. Оказалось, что в разных учебниках релятивистский радикал не обязательно сокращает эталоны длины и времени в движущейся системе K'. Он может увеличивать масштабные эталоны в системе K', так как для получения эталонов Δx' и Δt' не умножают, а делят эталоны Δx и Δt на релятивистский радикал. Причем операция деления может производиться только для одного эталона, другой эталон умножается на радикал. Таким образом, возникает четыре комбинации соотношения между эталонами движущейся K' и покоящейся K систем координат. Эта неопределенность нахождения эталонов и получила название парадокс штриха.
Сейчас я продемонстрирую парадокс штриха на конкретном примере двух книг: одна из них — известный учебник Ландау и Лифшица "Теория поля", автор второй книги Макс Борн; книга называется "Эйнштейновская теория относительности". Написана она в 20-м году прошлого века, так что на ней выросло не одно поколение физиков-релятивистов. Сейчас при изложении материала я воспользуюсь 6-м разделом курса лекций "Естествознание", выложенного на сайте Sceptic-Ratio.
Начнем с учебника Ландау и Лифшица. В нем, как это принято в подавляющем большинстве случаев, через штрихованную систему K' обозначена движущаяся система отсчета, а покоящуюся обозначают через K (без штриха).

Ландау (справа) и Лифшиц (слева)Читаю вместе с вами: «Пусть в системе K покоится линейка, параллельная оси x, – пишут Ландау и Лифшиц. – Длина ее, измеренная в этой системе, пусть будет Δx = x2 – x1 (x2 и x1 – координаты концов линейки в системе K). Найдем теперь длину этого стержня, измеренную в системе K'. Для этого надо найти координаты обоих концов стержня (x'2 и x'1) в этой системе в один и тот же момент времени t'. Находим (имеются преобразования Лоренца для длины):

Преобразования Лоренца и формула сокращения длины
по курсу физики Ландау и ЛифшицаСобственной длиной стержня называется его длина в той системе отсчета, в которой он покоится. Обозначим ее через l0 = Δx, а длину того же стержня в какой-либо системе отсчета K' – через l. Тогда (4.5) Таким образом, самую большую длину стержень имеет в той системе отсчета, где он покоится. Длина его в системе, в которой он движется со скоростью v, уменьшается в отношении (см. ниже) . Этот результат теории относительности называется лоренцевым сокращением».

Что называется собственной длиной стержняТеперь смотрим, что пишет Макс Борн по этому же вопросу. «Итак, – пишет Борн, – мы должны определить длину линейки в системе S'(x', ct'), движущейся относительно S(x, ct)... Пусть l0 – длина линейки в системе отсчета S', в которой линейка покоится; l0 называют статической или собственной длиной линейки. Два конца линейки имеют координаты, скажем, x'1 и x'2, так что x'2 – x'1 = l0 .
Макс БорнПри наблюдении этой линейки из системы S мы по первой из формул (70а) имеем (преобразования Лоренца для координат): (см. ниже фото)

Текст из книги Борна.Полагая ..., мы можем записать ... (74) Эта формула утверждает, что длина линейки в системе S оказывается уменьшенной в отношении ... к 1 в точном согласии с гипотезой сокращения, предложенной Фитцжеральдом и Лоренцем».

Выражение (74).Таким образом, Ландау – Лифшиц вывели формулу для лоренцева сокращения из прямых преобразований, а Борн – из обратных. То есть, выражения (4.5) и (74) в приведенных текстах только внешне выглядят одинаково, фактически они противоположного свойства.
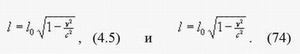
Выражения (4.5) и (74) только внешне выглядят одинаково,
фактически они противоположного свойства.Люди гуманитарного склада ума, например, философы и журналисты, будут спорить до хрипоты, обсуждая запутанные тексты обеих книг. Но математику и программисту, имеющему дело с компьютером, разобраться в них ничего не стоит. Они еще раз выпишут два одинаковые формулы — (4.5) и (74), а рядом поставят равенства, которые имели в виду авторы, выражая х-координаты через l-отрезки длины. Ландау и Лифшиц приняли: l0 = Δx и l = Δx' , а Борн ввел противоположные обозначения: l0 = Δx' и l = Δx.

Противоположные обозначеияСледовательно, Ландау и Лифшиц получили формулу (5.1), Борн — (5.2):
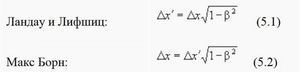
В данном случае абсолютно неважно, как авторы-релятивисты получали выражения (4.5) и (74); важно помнить об одном: штрихованная система — движется, нештрихованная — покоится. В итоге, авторы книг пришли к взаимоисключающему результату.
Сделаем короткий перерыв для разъяснения своей позиции в отношении длительности моих видеофильмов об эфире.
Видео-ролики из двух серий "Подделки" (древнеегипетских экспонатов, прежде всего, цветного бюста Нефертити) были преимущественно короткими, как это обычно рекомендуют для просмотра в YouTube, где-то около 15 минут. Теперь я не придерживаюсь этой рекомендации, так как не гоняюсь за количеством просмотров, а больше беспокоюсь о качественном составе аудитории, которая смотрит мои фильмы.
Видео-ролики из двух серий подделки бюста Нефертити были
короткими. Теперь я не придерживаюсь этой рекомендации.Зачем мне посетители, которые постоянно дергают бегунок YouTube так, что из часового фильма просматривается 2-3 минуты. Так поступают лодыри, верхогляды, несерьезные люди. Я же заинтересован во вдумчивом зрителе, чтобы он смотрел мои работы от начала и до конца, а некоторые важные и сложные места — по несколько раз.

Так поступают лодыри, верхогляды, несерьезные люди.В фильмах я часто делаю ссылки на страницы своего сайта Sceptic-Ratio, рассчитывая, что мой заинтересованный зритель продолжит изучение той или иной темы самостоятельно. В фильме не всегда можно всё показать и рассказать. Человеку непременно необходимо и что-то почитать, разобраться в математических доказательствах — иначе, зачем влезать в научную тематику.
Бойтесь легковесной популяризации, которой страдает почти вся продукция в Интернете. Как правило, в поисковиках она всплывает на первых позициях. В Сети можно найти всё, ознакомиться с любой точкой зрения; пытайтесь докопаться до сердцевины проблемы; не забывайте, что обычно дьявол сидит в деталях.

Я же заинтересован во вдумчивом зрителе.Поэтому, дорогой наш зритель и слушатель, наберитесь терпения и продолжите вместе со мной чтение учебника Ландау и Лифшица и книги Макса Борна, где рассказывается об изменении эталонов длины и времени. Поверьте мне, тема парадокса штриха — одна из важнейших. Люди проживают многие гола, пытаясь разобраться в релятивистских спекуляциях. Так посвятите же сегодняшний день данной запутанной проблеме, чтобы в будущем не плутать в темных лабиринтах теории относительности.
Итак, выясним, как уважаемые авторы учебника "Теория поля" и книги "Эйнштейновская теория относительности" представили своим несчастным читателям тему "Замедления времени" — центральную для релятивистской ортодоксии.
Начнем с учебника Ландау и Лифшица.
«Предположим, – пишут они, – что мы наблюдаем из некоторой инерциальной системы отсчета произвольным образом движущиеся относительно нас часы. В каждый отдельный момент времени это движение можно рассматривать как равномерное. Поэтому в каждый момент времени можно ввести неподвижно связанную с движущимися часами систему координат, которая (вместе с часами) будет являться тоже инерциальной системой отсчета».

Предположим, что мы наблюдаем из некоторой инерциальной системы отсчета.Далее авторы зачем-то использовали дифференциальную форму записи, хотя с точки зрения физики ситуация осталась прежней: изменение временной координаты (t) будет таким же, что и изменение пространственной координаты (x). Окончательную формулу (3.2) можно записать формулой (5.3)

Вывод производится через квадрат интервала путем принятия условия Δx' = 0Самым удивительным в учебнике Ландау и Лифшица является последний абзац приведенного пассажа: "Как видно из формулы (3.1) и (3.2), — пишут авторы, — собственное время движущегося объекта всегда меньше, чем соответствующий промежуток времени в неподвижной системе. Другими словами, движущиеся часы идут медленнее неподвижных».
Теперь посмотрим, что написал Борн в своей книге относительно изменения временной координаты. В первом предложении цитируемого отрывка он противоречит выводам учебника Ландау и Лифшица:

Для того чтобы вычислить величину удлинения ...Итак, Ландау и Лифшиц имели в виду укорочение (сокращение) долготы; Борн сразу заявил об удлинении (увеличении) времени. Далее, используя по-прежнему обратные преобразования Лоренца, он вывел формулу (75), которая в наших обозначениях выглядит как формула (5.4)

Это удлинение (замедление) времени
противоположно по характеру сокращению длины.В конце отрывка Борн еще раз недвусмысленно заявил: «Это удлинение (замедление) времени противоположно по характеру сокращению длины. Разумеется, с обратной точки зрения единица времени по часам, покоящимся в системе S, оказывается увеличенной в системе S'... Время, которое показывают часы, покоящиеся в выбранной системе отсчета, называется собственным временем системы».

Изменение координат в движущейся системе К' относительно покоящейся системы К у Борна совпали с формулами, представленными в работах Эйнштейна и Паули, хотя вывод их отличается от вывода Борна. Комбинация формул в Берклеевском курсе и в курсе Левича отличаются не только логикой вывода, но и результирующими комбинациями математических выражений. Откуда же взялся такой разнобой в формулах, который мы видим по таблице 5.1?
Дело в том, что при выводе окончательных формул релятивисты смешивают себя, как субъекта теории (его называем метанаблюдателем), с объектными наблюдателями, находящимися в координатных системах К и К'.
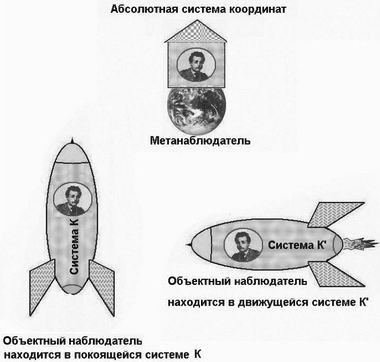
Авторы, цитируемых нами книг, становятся метанаблюдателями.Авторы, цитируемых нами книг, становятся метанаблюдателями неосознанно. Их внимание периодически соскальзывает то на позицию субъекта теории, то объекта, причем один раз их угораздит оказаться в штрихованной системе отсчета, другой раз — в нештрихованной. Так, появляется неопределенность в расстановке штриха, поскольку они, как метанаблюдатели, постоянно витают где-то над обеими системами, смешивая, что относительно чего движется. Им порою, кажется, что сначала штрихованный эталон больше нештрихованного, затем — наоборот.

МетанаблюдателиМетанаблюдатель выказывает свое присутствие, в частности, через термин собственный: если объектный наблюдатель к своим эталонам длины и времени добавляет этот предикат, значит, он претендует на статус метанаблящателя. Собственные эталоны длины и времени определяются как длина отрезка и, соответственно, время таких часов, которые покоятся относительно системы отсчета.

Выбор в принципе не возможен.Однако, если придерживаться этой дефиниции, легко выявится ее достаточно бессмысленное содержание. Часы, принадлежащие непосредственно данной системе координат, с точки зрения той же теории относительности, показывают то, что они показывают, как бы это тавтологично не звучало, т.е. Δt = Δt, Δt' = Δt' — не нужны эти вторичные обозначения. Когда под предлогом собственного времени и длины вводят новые обозначения, например, l0 = Δx и l = Δx' или Δt = T0 и Δt' = T и т.д. – если это вы видите, знайте, вас хотят ввести в заблуждение.
Ясно, что существовать могут только два эталона часов или два течения времени – время. Третьего времени, как бы его не называли – собственное или еще как-то – просто быть не может. Оно исключено логикой построения возможных ситуаций.
Мысленно релятивисты скользят как бы по ленте Мёбиуса.Мысленно релятивисты скользят как бы по ленте Мёбиуса. Рассуждая сначала в одной плоскости, они незаметно для себя оказываются в другой плоскости, развернутой относительно первой на 180 градусов. Такой логический кульбит объектный наблюдатель способен совершать благодаря абсолютной системе координат метанаблюдателя. Раздвоение сознания — это естественное и постоянное состояние любого релятивиста.

Раздвоение сознания — это естественное и
постоянное состояние любого релятивиста.Парадокс штриха, связанный с масштабами длины и времени, напоминает парадокс лестницы Шрёдера. Глядя на рис. 6.1, может возникнуть образ либо лестницы, либо нависающего ступенчатого карниза. Почему так происходит?
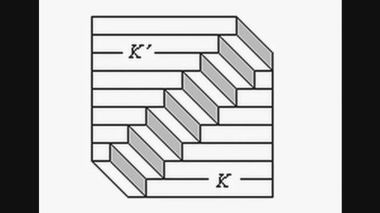
Лестница Шрёдера.Другое дело, если смотреть не на симметричный рисунок 6.1, а на реальную лестницу или карниз. За счет перспективы, которая выражается, скажем, в чуть меньшем расстоянии между горизонтальными полосками треугольника K'. Тотальный релятивизм не оставляет нам ни единого антисимметричного элемента в отношении систем K' и K.

Реальная лестница за счет перспективы имеет антисимметричный элемент.Поэтому сначала к нам приходит уверенность в правильности использования обратных преобразований Лоренца, но через некоторое время эта уверенность куда-то улетучивается, картина переворачивается, и мы уже считаем правильным использование прямых преобразований. Это происходит периодически, мы не можем остановиться на каком-то одном решении, которое следовало бы назвать истинным.
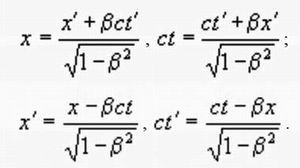
Прямые и обратные преобразования ЛоренцаПсихологический парадокс штриха определенным образом связан и с известным логическим «парадоксом обманщика» (см. Парадоксальные высказывания), который строится следующим образом: «Я обманщик», – сказал обманщик. Итак, обманщик сообщает о себе, что он является таковым. Следовательно, он выступает в своем противоположном качестве, а именно, необманщика. Поэтому сказанное предложение нужно прочитать так: «Я обманщик», – сказал необманщик. Правдивому человеку мы должны верить, но ведь он сообщает, что он является обманщиком. Таким образом, мы снова возвращаемся к первому предложению.

«Я обманщик», – сказал обманщик.Возникает неопределенность в том, как квалифицировать фразу, заключенную в кавычках: как нечто, соответствующее истине, то есть считать, что она верно характеризует человека, произносящего данное предложение, или же ее надо расценить как ложную фразу.
Парадокс обманщика возник потому, что в данной семантико-лингвистической конструкции не проведена демаркационная линия между субъектом и объектом. Помимо обманщика и необманщика в этой ситуации участвуем мы с вами в роли исследователя, стороннего наблюдателя или, как мы говорим, метанаблюдателя.
Возникает неопределенность в том, как квалифицировать
фразу «Я обманщик» – как истинную или как ложную.Если произвести четкое лингвистическое отделение смыслового содержания, которое должно относиться к нам, как метанаблюдателям, от прочей семантики объектных персонажей, то логическое противоречие будет снято. Вот каким способом нужно представить ситуацию с обманщиком, чтобы исключить из нее двусмысленность:

Как произвести лингвистическое отделение смыслового
содержания, высказанное наблюдателем и метанаблюдателем?
1. «Я обманщик», – сказал обманщик.
«Это истина», – сказал метанаблюдатель.
2. «Я обманщик», – сказал необманщик.
«Это ложь», – сказал метанаблюдатель.
3. «Я необманщик», – сказал обманщик.
«Это ложь», – сказал метанаблюдатель.
4. «Я необманщик», – сказал необманщик.
«Это истина», – сказал метанаблюдатель.

Помимо обманщика и необманщика в этой ситуации
участвуем мы с вами в роли метанаблюдателяПарадокс обманщика предупреждает нас о возможных на этом пути осложнениях. Из цепочки отношений – Петр враг Ивана, Иван друг Степана, а Степан враг Кузьмы – однозначно следует, что Петр друг Кузьмы. Этот вывод сделан субъектом теории, т.е. метанаблюдателем.

«Я — Ян», «Я — лгунишка».Но нельзя строить конструкцию типа: «Петр обманщик», – сказал Иван. «Это ложь», – сказал Степан. Степан, как объектный персонаж, не должен выносить свою оценку в отношении Петра, Ивана и прочих лиц, непосредственно участвующих в объектной ситуации. Это разрешено делать только метанаблюдателю с безупречной «моральной» характеристикой, который не имеет права лгать.

За любым «наблюдателем» всегда
следит какой-нибудь метанаблюдатель.Таким образом, парадокс обманщика говорит нам о том, что попытка метанаблюдателя встать на позицию обманщика или необманщика немедленно приводит к смысловому конфликту.
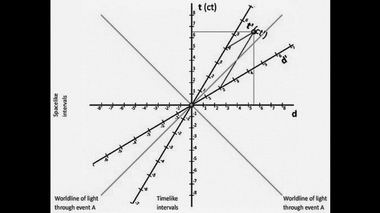
К вопросу о диаграмме Минковского.
Добавление из первоначального курса лекций "Естествознание"
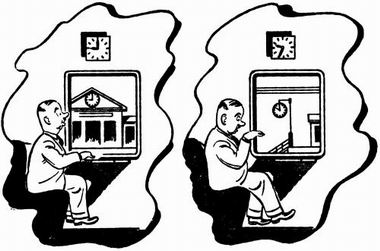
Два пассажира сидят каждый в своем купе и смотрят в окнаПредставим себе два железнодорожных состава, неподвижно стоящих на соседних путях. Два пассажира, находясь в своих поездах, смотрят в окна вагонов друг на друга. Увиденную ими картину можно отразить следующей таблицей умножения:
1) движение * движение = покой,
2) покой * движение = движение,
3) движение * покой = движение,
4) покой * покой = покой.При плавном движении двух поездов в одном направлении и с одинаковой скоростью пассажирам кажется, что их поезда стоят на месте (1), как если бы оба поезда действительно стояли на месте (4), т. е. возникает неопределенность в выборе пунктов 1 и 4. При плавном движении одного из поездов пассажиры также не в состоянии определить, какой именно из поездов тронулся (неопределенность между пунктами 2 и 3). Объективную ситуацию с движением поездов может правильно оценить лишь провожающий, находящийся на платформе, т. е. метанаблюдатель.

Точно такая же неопределенность возникает в теории относительности при сравнении эталонов длины и времени, находящихся в движущейся и покоящейся системах отсчета. Нельзя построить физическую теорию, основывающуюся исключительно на относительных величинах. Логика и математика подсказывают нам необходимость введения метанаблюдателя, находящегося в абсолютной системе отсчета. Тогда преобразования Лоренца можно будет привязать к этой абсолютной системе отсчета, которой для Лоренца служил эфир.
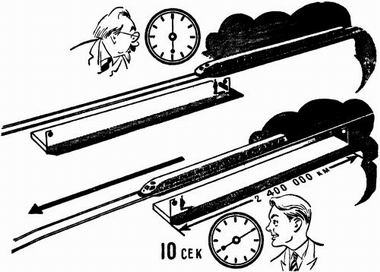
Если абсолютная система отсчета отсутствует, каждый из объектных наблюдателей произвольно выбирает либо прямые, либо обратные преобразования координат и получает на их основе то, что ему нравится. Без абсолютной системы отсчета объектный наблюдатель оказывается как бы без точки опоры, т.е. в роли барона Мюнхгаузена, который вытащил самого себя из болота за волосы.

В своих мысленных экспериментах релятивисты не вводят метанаблюдателя, но всякий теоретизирующий человек не может абстрагироваться от самого себя, поэтому метанаблюдатель находится на положении «нелегала». Он проявляется то в образе одного объектного наблюдателя, то другого; совершенно незаметно для себя он будет то «расщепляться» на два наблюдателя, находящихся каждый в своей системе, то вновь «конденсироваться» в одно лицо.
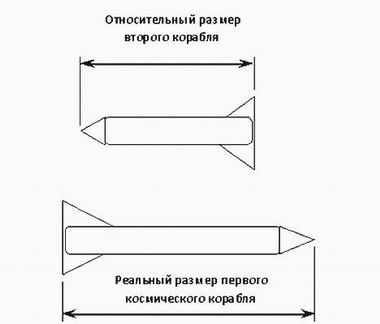
Метанаблюдатель, находясь в некотором привилегированном положении, всегда претендует на абсолютную непогрешимость в своих суждениях. Когнитивные процессы, идущие в недрах сознания субъекта теории, генерируют собственный пространственно-временной объем. Хочет он того или нет, метанаблюдатель всегда занимает абсолютную систему отсчета; такая позиция неизбежна, иначе невозможно было бы сравнение, а значит, и мышление.
Сокращение длины движущихся объектов.
С этим, кажется, все согласны и релятивисты
не ожидают здесь какого-то логического подвоха.Смешение функций объектного наблюдателя с субъектным открывает шлюзы для всевозможного рода спекуляций, которые мы и наблюдаем на примере неопределенного изменения эталонов длины и времени. В общем, в зависимости от ситуации в системах отсчета могут устанавливаться такие отношения, которые удобны с точки зрения общей идеологии теории относительности, но ошибочные по существу.
"Почему он?! На этот вопрос учителя
ответить учащемуся очень сложно.В самом начале этого видеофильма мы упомянули диаграмму Минковского, сказав, что было бы желательно вычертить конкретную диаграмму и определить по ней реальный масштабный коэффициент сокращения длины и времени. Релятивисты, как правило, даже не пытаются этого сделать. Анализ проводится на уровне формул. Но сейчас мы столкнулись с неоднозначностью в оценки эталонов длины и времени. Поэтому было бы логично прибегнуть к геометрическим чертежам, которые помогли бы нам установить истину, а именно, узнать, будет ли
Δx < Δx' или Δx > Δx', Δt < Δt' или Δt > Δt' .

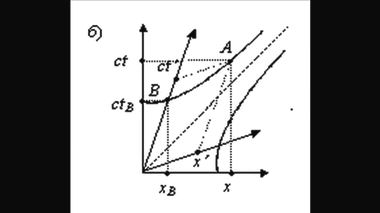
Герман Минковский21 сентября 1908 года на 80-м собрании немецких естествоиспытателей и врачей в Кёльне Герман Минковский сделал доклад под названием "Пространство и время". В ходе доклада докладчик вычертил рис. 1 и попытался доказать, что эталоны движущейся и покоящейся системы K(x, t) и K'(x', t') связаны посредством релятивистского радикала.
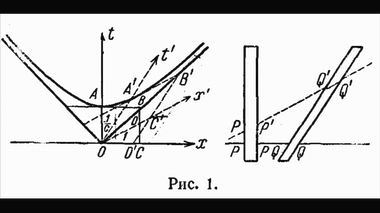
Рис. 1 из работы Минковского. Автора расхваливают на все лады за эту диаграмму и введение им четырехмерного пространства. На самом же деле Минковский наделал здесь грубые математические ошибки, которые раскроются перед нами по ходу продвижения нашего анализа, хотя кое о чём можно сказать сразу. Из левого чертежа (рис. 1) автор вывел ложную формулу для сокращения длины, т.е. отношение длины отрезков OC к OD' или PP к QQ. Но почему-то он даже не попытался вывести аналогичное отношение для времени. Почему? Да потому, что в 1909 году господствовала точка зрения Эйнштейн, согласно которой отношение эталонов длины противоположно отношению эталонов времени, т.е. Δx/Δx' = Δt'/Δt. Диаграмма же, вычерченная автором, оказалась абсолютно симметричной относительно биссектрисы ОВ(В'). Следовательно, Минковский должен был получить Δx/Δx' = Δt/Δt'. Однако открыто объявить о расхождении своего геометрического вывода с аналитическим выводом формулы замедления времени, сделанным Эйнштейном (тоже, конечно, ложным), он не решился.Автор доклада упомянул об отрицательном результате эксперимента Майкельсона и напомнил, что "по Лоренцу, каждое движущееся тело должно сократиться в направлении движения при скорости v в отношении ... (см. текст 1 ниже на фото)

Текст 1 из статьи МинковскогоЯ хочу теперь на нашем чертеже, — сказал Минковский, — показать, что гипотеза Лоренца и новые воззрения на пространство и время вполне эквивалентны и что благодаря этому гипотеза делается гораздо понятнее. Если с целью упрощения отвлечься от координат y и z , представить себе пространственно одномерный мир, то параллельная полоса, стоящая прямо, как ось t, и параллельная полоса, наклоненная относительно оси t (рис. 1), суть графики покоящегося и равномерно движущегося тела, сохраняющего в обоих случаях одно и то же постоянное пространственное протяжение".
После некоторых разъяснений в построении чертежа (рис. 1) докладчик заявил: "Из простого расчета следует, что если dx/dt = v, то ... (см. текст 2 ниже на фото)

Текст 2 из статьи Минковского.Итак, Минковский утверждает, что в движущейся системе K' отрезок OD' на левом чертеже или отрезок QQ на правом чертеже меньше эталона длины в покоящейся системе K, где за эталон принят отрезок OC и отрезок PP. В наших обозначениях справедливо выражение (5.1).
Поскольку диаграмма Минковская симметрична относительно биссектрисы ОB или OB', соответствующей скорости света (c = x/t = x'/t'), то соотношения эталонов времени будет таким же, как и отношение отрезков длины, т.е. справедливо выражение (5.3).

Таким образом, правильной оказывается комбинация эталонов, представленная в учебнике Ландау и Лифшица; три других комбинации из таблицы 5.1, включая самую первую, предложенную Эйнштейном, а потом Борном и Паули, будут уже ложными.

Парадокс штрихаИтак, три первых автора пали жертвой парадокса обманщика. Минковский же с помощью элементарной геометрии нашел, кажется, единственно правильное решение. Первым ошибся Эйнштейн, когда искал соотношения между масштабными единицами движущейся и покоящейся системы координат. Борн и Паули шли сразу за ним уже по ложному пути. Ландау и Лифшица, видимо, учли геометрический урок, преподанный Минковским. Но почему другие релятивисты не последовали за Минковским — это загадка, которая, однако, имеет некоторое объяснение.
Дело в том, Минковский тоже ошибся в количественном отношении: формулы (5.1) и (5.3) ошибочны, так как ошибочны выражения в самом докладе Минковского.

А. ЗоммерфельдТо, как выводил эти формулы Минковский, повторил Зоммерфельд. Но если бы эти авторы подставили какие-нибудь числовые значения в эти выражения, они тут же убедились бы, что формулы не работают. Соотношение между отрезками OC и OD' или между PP и QQ совсем не такое, как хотели бы видеть указанные авторы и все прочие релятивисты.



Текст ошибочного доказательства
сокрашения длины по диаграмме МинковскогоДля понимания того, в чём ошибся Минковский, воспользуюсь курсом Дискретной математики подразделом Ортогональные и гиперболические преобразования раздела 2.5. "Пространственные группы и двойственность".
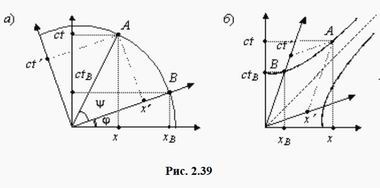
Под ортогональными и гиперболическими преобразованиями понимаются повороты осей, показанные на рис. 2.39 (а) и (б), соответственно. Обозначения осей координатных систем K(x, ct) и K'(x', ct') здесь выбраны с прицелом на теорию относительности, хотя рассматриваемый вопрос относится к общематематической тематике.
Ортогональный поворот осей ищется по тригонометрическим формулам сложения двух углов, если радиус окружности равен единице:
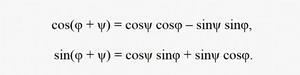
Непосредственно из чертежа видно, что
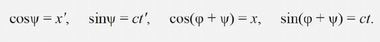
Следовательно,
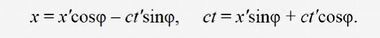
Так как
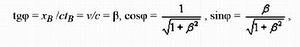
окончательно получаем первые две формулы ортогонального преобразования в форме декартового поворота, который соответствует первым двум формулам первого столбца табл. 2.92 (в таблице ось ct обозначена через y)
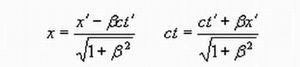
Если найденные преобразования принять за прямые, то обратными будут две другие формулы, первого столбца табл. 2.92.

Рассмотренные преобразования действуют в евклидовом пространстве. Чтобы получить из них гиперболические преобразования для псевдоевклидового пространства, нужно произвести замену вещественной оси y на мнимую ось iy (i — базисная единица). В этом случае произойдет замена вещественного параметра β на –iβ, так как x/iy = –iβ. Формулы гиперболического поворота, полученные из формул ортогонального преобразования, заняли второй столбец табл. 2.92.
Согласно принципу двойственности, который действует в некоторых областях геометрии, логики, физики и других наук (о нём рассказывалось в предыдущем подразделе Двойственность и проецирование), мы можем получить гиперболические преобразования в евклидовом пространстве (это третий столбец табл. 2.92). Тогда ортогональные преобразования окажутся в неевклидовом пространстве с мнимой вертикальной осью iy (это четвертый столбец).
Нас интересует изменение масштаба осей при гиперболическом повороте. Как чаще всего поступают релятивисты? Они обнуляют одну из координат. Например, чтобы найти изменившуюся длину Δx' штрихованной системы K' по известной длине Δx нештрихованной системы K, берут координаты двух точек на оси абсцисс и составляют из них разность. Как правило, релятивисты пользуются формулами без мнимой единицы, т.е. формулами третьего столбца таблицы 2. 92.
Итак, беря две точки на оси x-ов, и составляем из них разность:
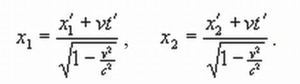
При условии одновременного измерения пространственных координат, т.е. выполнения условия t1 = t2, получается формула сокращения длины:
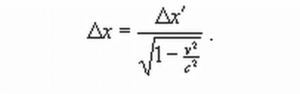
Очевидно, аналогичная методика нахождения соотношения между масштабами штрихованной и нештрихованной системы координат должна срабатывать и для ортогональных преобразований декартовых координат. Выписываем координаты
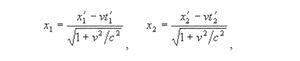
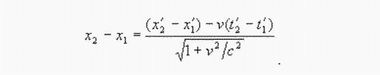
Обращаем внимание, что в знаменателе стоит не релятивистский радикал. При условии t1 = t2 получаем формулу удлинения длины:
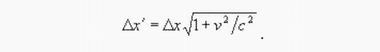
Но при повороте декартовых координат масштабы осей, как известно, не меняются. В действительности полученное соотношение
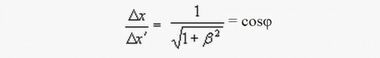
этот косинус указывает на угол поворота оси. Следовательно, методика релятивистов ошибочна.
Каким же образом нужно поступать, чтобы рассчитать соотношение между масштабами штрихованной и нештрихованной систем координат при гиперболическом повороте, который показан на рис. 2.39б?
Для нахождения масштабного или нормировочного коэффициента kn слегка дополним рис. 2.39а, как это показано на рис. 2.40.
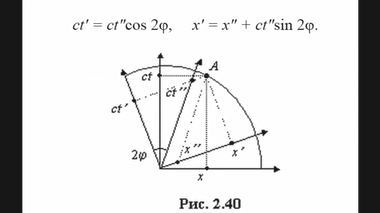
Из последнего чертежа найдем координаты:
ct' = ct"cos 2φ, x' = x" + ct"sin 2φ.
Подставим найденные штрихованные значения в формулу преобразования декартовой пространственной координаты:
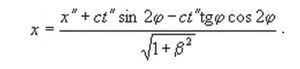
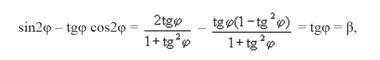
окончательно находим масштабный коэффициент kn:
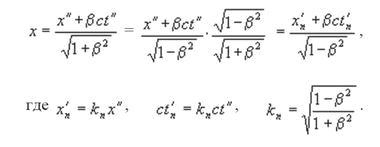
Аналогичным образом можно выделить масштабный коэффициент kn из второго ортогонального преобразования:
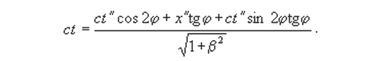
Так как cos2φ + tgφ sin 2φ = 1, окончательно находим:
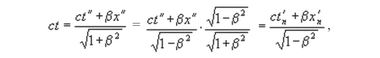
Для проверки найденного масштабного коэффициента kn можно вычертить реальный чертеж на бумаге с гиперболическим поворотом осей x' и ct', отвечающий преобразованиям Лоренца, и произвести измерение всех координат непосредственно по чертежу.
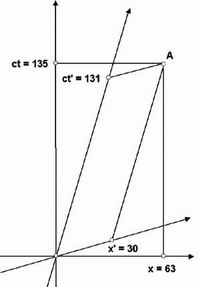
Реальный чертеж на бумаге с гиперболическим поворотом осей x' и ct'Кроме точки A, возьмем еще четыре точки — B1, B2, C1, C2, — с другими координатами. Все измеренные величины занесены в табл. 2.93.
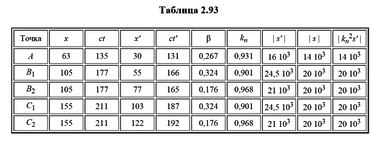
По найденным координатам вычислим β и масштабный коэффициент kn, а также квадратичные инварианты s и s' по формуле, известной из теории относительности:
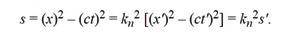
Надо заметить, что коэффициент kn определяется из квадратичной формы намного проще. Добавим, поскольку коэффициента kn < 1, то можно говорить о «сжатии» обеих штрихованных осей. Однако из этого математического факта вовсе не следует, что в реальном физическом мире сокращается пространство и замедляется время. Любые математические манипуляции с веденными нами координатами никак не сказываются на физических явлениях. Релятивист тем и отличается от антирелятивиста догматической верой, будто выбор геометрического пространства и его математические преобразования отражаются на физических процессах.
Нельзя не заметить также, что в получении преобразований, соответствующих диаграмме Минковского, был использован искусственный прием: умножение числителя и знаменателя формул преобразований на релятивистский радикал.

Это понадобилось нам для того, чтобы гиперболическими преобразования (*), геометрически соответствующие диаграмме Минковского, чисто внешне отвечали преобразованиям Лоренца. Для самих же преобразований (*) — их нельзя уже называть лоренцевыми — не нужно вводить никаких масштабных коэффициентов. Для проверки данного математического факта найдите конкретные числовые значения координат x и ct (см. табл. 2.93) путем прямой подстановки в преобразования (*) числовых значений координат x' и ct'.
Таким образом, диаграмма Минковского, вообще говоря, не удовлетворяет преобразованиям Лоренца. Но их внешнего сходства можно добиться путем введения найденного выше масштабного или нормировочного коэффициента kn .
Релятивисты часто пользуются трехмерной диаграммой Минковского, на которой имеется две пространственные оси (x, y), образующие горизонтальную плоскость, и одна вертикальная ось t. Третью пространственную ось z они не вычерчивают, но ее существование подразумевается. На диаграмме указывается положение объектного наблюдателя в центре координат.
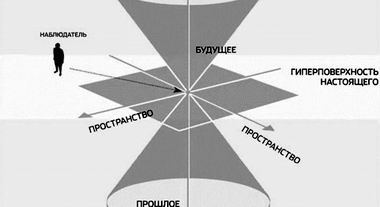
Трехмерная диаграмма МинковскогоЭто его положение соответствует настоящему времени; вверх от него откладывается будущее время (+ t), вниз от него — прошлое время (– t). Поверхность конуса, заверяют релятивисты, ограничивает возможные траектории наблюдателя в четырехмерном пространстве-времени. Они рассказывают о мировых линиях (vt), пролегающих внутри конуса; на границе же конуса скорость v достигает скорости света.
Трехмерные диаграммы Минковского обычно рисуются схематично, без каких-либо количественных оценок. Между тем, все числовые величины, присвоенные этим трехмерным сооружениям, будут содержать все те же ошибки, которые отмечались для двумерных диаграмм Минковского.
Таким образом, диаграмма, которую релятивисты называют именем Германа Минковского, носит исключительно двумерную природу. Попытка экстраполировать ее на пространство трех и большего числа измерений — математически бессмысленна.
В силу принципа двойственности, который обнаруживается через замену вертикальной оси y = ct на мнимую ось iy = ict и что отражено в таблице 2.92 двумя рядами дублирующих формул, мы можем вместо косинуса и синуса использовать гиперболические функции.
Таким образом, комплексную плоскость с системой уравнений из тригонометрических функций
cos(φ + ψ) = cosψ cosφ – sinψ sinφ,
sin(φ + ψ) = cosψ sinφ + sinψ cosφможно заменить вещественной плоскостью с системой гиперболических функций:
ch(φ + ψ) = chψ chφ + shψ shφ,
sh(φ + ψ) = chψ shφ + shψ chφ;Таким образом, из чертежа (рис. 2.39б) мы выведем преобразования Лоренца, в которых, однако, уже учтены изменения масштабных единиц штрихованной системы (см. Масштаб осей при гиперболическом повороте).

Остается рассмотреть маленький, но очень важный вопрос, связанный с грубой математической ошибкой предельного перехода. Напомним, как релятивисты осуществляют его. Они записывают преобразования Лоренца в виде
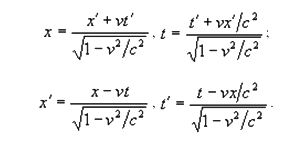
Затем говорили, что условие v << c равносильно условию c → ∞, следовательно, преобразования Лоренца переходят в преобразования Галилея
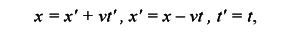
Ошибка данного предельного перехода легко обнаруживается при рассмотрении двух принципиально различных движений координатных систем K и K' относительно друг друга. Преобразования Лоренца — это вращательное движение осей — пусть гиперболического характера — преобразование Галилея — это поступательное или продольное смещение осей
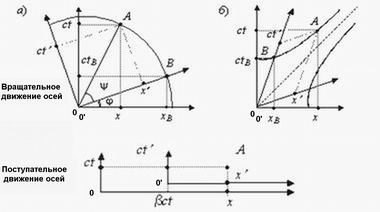
Не может вращательное движение осей в пределе переходить в их поступательное движение, когда начало координат системы K' (т.е. точка 0') удаляется на какое-то расстояние от начала координат системы K (точка 0).
Где допустили ошибку релятивисты?
Ошибка возникла тогда, когда условие предельного перехода β = v/c → 0 заменили неравносильным условием c → ∞
Поэтому преобразования Лоренца лучше писать не в виде, в котором скорости v и c фигурируют раздельно, а в виде преобразований, в которых v и c связаны одним параметром β = v/c
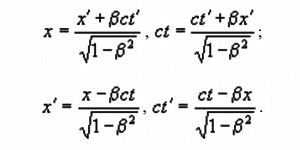
При условии β → 0 или φ → 0 гиперболические функции ведут себя следующим образом:

Отсюда следует, что преобразования Лоренца в случае предельного перехода параметра β → 0 трансформируются в единственно возможные равенства: x = x', ct = ct'. Никаких других выражений здесь в принципе быть не может.
Итак, казалось бы, крохотная подмена условий предельного перехода привела к колоссальным заблуждениям, будто преобразования Лоренца это те же самые преобразования Галилея, но только записанные для очень большой скорости v , сопоставимой со скоростью света c . Это, разумеется, не так.
Многим релятивистам известна обратная процедура, а именно вывод преобразований Лоренца из преобразований Галилея. Он не связан с каким-либо предельным переходом. Преобразования Лоренца получаются из преобразования Галилея путем единственного допущения: скорость света в штрихованной K' и нештрихованной системе K координат должна быть одна и та же:
x/t = x'/t' = c = const.
x = (x' + vt' )α, x' = (x – vt)α,Из этих равенств не сложно получить искомый множитель α
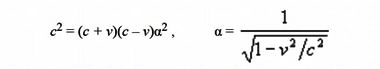
Таким образом, переход от Галилея к Лоренцу будет скачкообразным, он не является предельным переходом, т.е. непрерывным изменением параметра β. Условие постоянства параметра c в штрихованной и нештрихованной системах не накладывает на саму величину c никаких количественных ограничений, т.е. c может быть вполне сопоставима со скоростью v или даже меньше ее (c < v), преобразования Лоренца по-прежнему остаются в силе.
Трансформация поступательного преобразований Галилея во вращательное преобразование Лоренца означает трансформацию одной группы симметрии в совершенно другую группу симметрии. Группа преобразований Галилея не является подгруппой преобразований Лоренца или наоборот. Это — две различных группы симметрии.
Ошибка предельного перехода моментально приводит к множеству противоречий, которые не имеют никакой перспективы для разрешения. Парадокс распиленной линейки является наиболее наглядным — о нем сейчас мы расскажем.
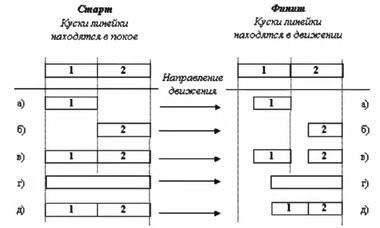
Рис. 8.2. Парадокс распиленной линейки.Пусть происходит транспортировка двух кусков линейки — 1 и 2. Если куски транспортируются по отдельности, то сокращение их произойдет так, как показано на финише (а) и (б). Совместная транспортировка этих кусков ничего не изменит и на финише между кусками будет виден просвет (в). Однако транспортировка целой линейки приведет к сокращению типа (г). Значит, между кусками не должен наблюдаться просвет (д) — ведь линейка «не знает», что она распилена. Итак, непонятно, как будет в действительности происходить сокращение транспортируемых кусков линейки — по варианту (в) или по варианту (д)?
Дадим разъяснения к парадоксу распиленной линейки.
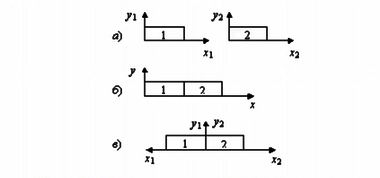
Рис. 8.3. Дрейф нуля системы отсчета.Случай (а) соответствует варианту (в) на рис. 8.2, когда каждый кусок линейки связан со своей собственной системой отсчета. Случай (б) соответствует варианту (д) на рис. 8.2, когда оба куска линейки связаны одной системой координат. Случай (в) демонстрирует иное, чем для случая (а), расположение координатных осей. Какую систему координат выбрать для наших кусков линейки? В действительности, это дело вкуса каждого человека.
В парадоксе с распиленной линейкой проявляется эффект, который можно было бы назвать дрейфом нуля системы отсчета.
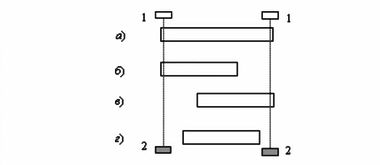
Рис. 8.4. При движении стержня мы будем иметь
различное положение сокращенного стержня.Пусть покоящийся стержень имеет такую длину, которую едва бы хватило для закрытия фотодатчиков 2 от лучей источников 1 (а). Тогда при движении стержня мы будем иметь различное положение сокращенного стержня: все будет зависеть от положения нулевой отметки системы координат, связанной с нашим стержнем. Поэтому на определенный момент времени может получиться так, что окажется закрытым левый фотодатчик (б), правый (в) или оба датчика окажутся освещенными источниками света (г).
Дрейфом нуля системы отсчета объясняется и известный парадокс зажженной лампочки. На рис. 8.1 показаны следующие варианты
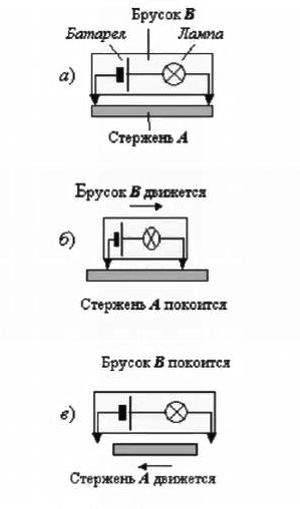
Рис. 8.1. Парадокс зажженной лампочки.
Что произойдет — вспыхнет или не вспыхнет лампочка.Все элементы электрической цепи находятся в покое: лампочка горит, так как цепь замкнута (а). Из-за быстрого перемещения бруска В расстояние между контактами для наблюдателя А сократится, но лампочка на мгновение вспыхнет, так как цепь на некоторое время окажется замкнутой (б). При быстром движении проводящего стержня А для наблюдателя В цепь окажется постоянно разомкнутой и лампочка никогда не вспыхнет (в). Согласно принципу относительности, два последних случая — (б) и (в) — тождественны. Вопрос: что произойдет в действительности — вспыхнет или не вспыхнет лампочка — вот парадокс?
Таким образом, парадоксы распиленной линейки и зажженной лампочки доказывают, что кинематическое сокращение длины движущихся тел происходить не может, так как поступательное перемещение координатных систем по Галилею не имеет ничего общего с вращательным движением координатных систем по Лоренцу.
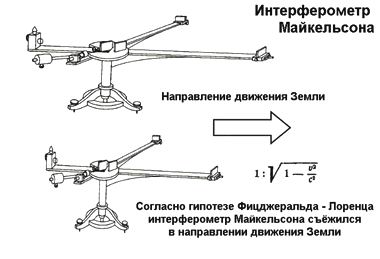
Сегодняшних школьников учат, что интерферометр Майкельсона,
согласно гипотезе Фицджеральд – Лоренца, испытывает сжатие
в направлении движения Земли.Сегодняшних школьников учат, что интерферометр Майкельсона, согласно гипотезе Фицджеральда – Лоренца, испытывает сжатие в направлении движения Земли, поэтому, дескать, не происходит сдвиг интерференционных полос. Но тут же возникает недоуменный вопрос. Так как Майкельсон во время проведения опыта находился в движущейся координатной системе прибора K', то ни он, ни Лоренц с Фицджеральдом, ни кто-либо другой живущей на Земли не могли зафиксировать сжатие интерферометра.

Как теоретик превращается в обманщика.Те, кто сейчас говорит о гипотезе сокращения длины, реально превращаются в обманщиков, поскольку путают объектного наблюдателя — Майкельсона — с метанаблюдателями — Лоренцем и Фицджеральдом. На первых порах, когда теория относительности еще не сформировалась, Лоренц и Фицджеральд ничего не говорили о замедлении времени. Сегодня, рассказывая школьникам о гипотезе сокращения длины, учителя обязаны что-то говорить об одновременном замедлении времени. Но этого, к сожалению, не происходит, поскольку они самостоятельно не в силах выбраться из релятивистских спекуляций.
Радиолокационный метод.Помимо представленных парадоксов нами были найдены математические ошибки во множестве других разделах релятивистской физики. Так, например, Макс Борн, глядя на Германа Минковского, попытался вывести формулы сокращения длины и замедления времени геометрическим путем (см. Радиолокационный метод). Его способ не сделался популярным, как диаграмма Минковского, поскольку Борн допустил еще больше ошибок, чем Минковский. Впрочем, источник ошибок для обоих авторов был один — это подгонка всех геометрических построений под "гипотезу Фицджеральда и Лоренца" о сокращении длины. Это амбициозная цель с самого начала была обречена на провал.
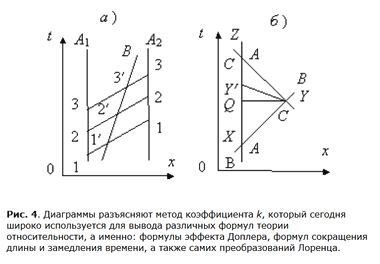
Диаграммы разъясняют метод коэффициента k.Борн вместе Бомом, Бонди и Ходсбэри принимал участие в разработке радиолокационного метода или метода коэффициента k, который широко использовался для вывода различных формул теории относительности, в том числе, формулы доплеровского эффекта, формул сокращения длины и замедления времени, да и самих преобразований Лоренца. По этой методики авторы ухитрились вывести, например, релятивистскую формулу для эффекта Доплера — вот в таком виде якобы подтвержденную экспериментом.
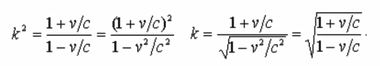
Ошибки этого метода обнаруживаются просто: путем подстановки конкретных числовых данных. Эти ошибки неизбежны, поскольку все авторы метода уверовали, будто штрихованные оси сокращались на величину релятивистского радикала. Откуда взялась эта их вера, геометрически ничем не подтвержденная. Коротенько напомним основные вехи релятивистского наваждения.

Лоренцевы преобразования возникли из ложного толкования эксперимента Майкельсона — Морли. Физики конца 19-го века, не умея объяснить результаты опыта — а мы их объяснили в 1-й части нашего фильма — приняли гипотезу Фицджеральда — Лоренца, которая в умах релятивистов быстро приобрела статус догмы. Согласно их абсурдной теории оптический прибор, используемый Майкельсоном, уменьшил свои размеры в направлении движения Земли. Поскольку в приборе использовались световые сигналы, т.е. электромагнитное излучение, то ключ к разгадке, они посчитали кроется в уравнениях Максвелла.

Начали искать некие преобразования координатных систем, которые бы оставляли эти уравнения в неизменном виде, говорят, в инвариантном виде. Таким образом, релятивисты рассчитывали распространить принцип относительности, справедливый для классической механики, на электромагнитную сферу. Преобразования Галилея оставляют четыре закона Ньютона в неизменном виде; теперь появились преобразования Лоренца, оставляющие четыре закона Максвелла тоже в неизменном (инвариантном) виде. За счет спекуляций на условии предельного перехода релятивисты стали утверждать, будто бы преобразования Галилея являются частным случаем общих преобразований Лоренца.

В отношении инвариантности уравнений Максвелла имеется серьезное возражение. Дело в том, что Фарадей и Максвелл, разрабатывая теорию электромагнетизма, опирался на эфир в виде некой гидродинамической модели. Поэтому из уравнений Максвелла легко выводится волновое уравнение, справедливое для воды, воздуха и прочих сплошных сред (см. Инвариантность волнового уравнения).
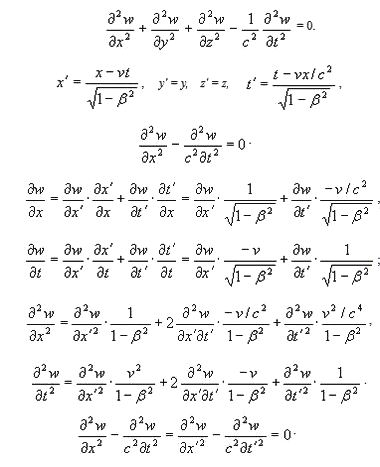
Верно, что Лоренц вывел преобразования, названные Пуанкаре "лоренцевыми", из области электромагнетизма, которая, однако, в то время целиком покоилась на эфирных представлениях. Поскольку Лоренцевы преобразования, оставляющие уравнения Максвелла и выведенное из них волновое уравнение в инвариантном, т.е. неизменном, виде, возникает законный вопрос: а как быть с медленными акустическими волнами, распространяющимися, например, в воде и воздухе? Что скажут релятивисты, в частности, по вопросу предельного перехода. Ведь для акустических волн фигурирует, разумеется, не умопомрачительная скорость света, а вполне себе умеренная скорость звука где-нибудь в воде или воздухе.

Убийственный аргумент. Релятивист должен застрелиться,
когда обнаружит неинвариантность уравнений теплопроводности и
диффузии. Ведь они не подчиняются принципу относительности Эйнштейна.Но самым убийственным аргументом для релятивистов является не этот. Они напрочь забывают, что преобразования Лоренца оставляют в инвариантном виде исключительно волновые уравнения — какую бы природу они не носила — электромагнитную или акустическую — но они не оставят в неизменном (инвариантном) виде все прочие уравнения механики.

Посмотрите, так выглядит волновое уравнение, а так выглядит уравнение теплопроводности и диффузии, где вместо параметра 1/с2 стоит параметр 1/с где, c — постоянная теплопроводности или диффузии. Таким образом, невозможно говорить о каких-то универсальных преобразованиях, которые бы оставляли инвариантными все без исключения дифференциальные уравнения. Само такое требование является математически некорректным.
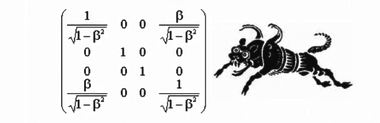
Эта распространенная 4 × 4 матрица придает видимость в принципе
двумерным преобразованиям Лоренца вид четырехмерных преобразований.Чтобы ближе подступиться к теме многомерности пространств, нам нужно освежить в памяти некоторые алгебраические понятия. В подразделе "Дискретной математики", который называется Представление группы кватерниона, раскрывается смысл произведения двух комплексных чисел z и z', которые могут быть представлены в трех эквивалентных формах.
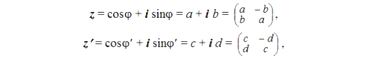
Тогда произведению z на z' отвечают два последовательных поворота в комплексной плоскости x, iy :
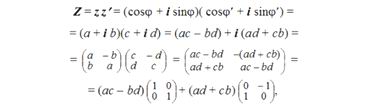
Кватернион получается путем удвоения комплексного числа: кватернион
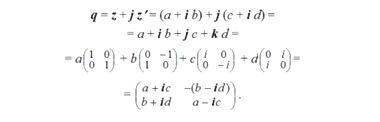
Составим произведение двух кватернионов:
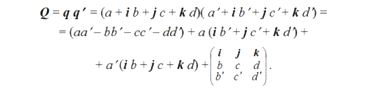
Здесь скалярная часть произведения есть произведение скалярных частей множителей минус скалярное произведение их векторных частей. Векторная часть произведения состоит из суммы произведений скалярной части каждого множителя на векторную часть другого плюс произведение векторной части первого множителя на векторную часть второго. Таким образом, все существующие виды умножения в векторной алгебре являются осколками единой операции перемножения двух кватернионов.
Перемножение двух сопряженных кватернионов дает скаляр
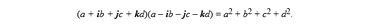
Кватернион с нормированными коэффициентами
a² + b² + c² + d² = 1,
можно представить через тригонометрические функции
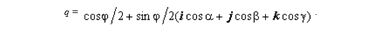
где α, β, γ — углы между некоторым вектором p и осями координат, φ — угол вращения вокруг вектора p.

Пространственное вращение, описываемое кватернионом q, за которым следует вращение q', дает результирующее изменение ориентации, описываемое кватернионом Q. Предположим, кватернион q отвечает повороту вокруг оси x на угол φ = π/2, а q' — точно на такой же угол, но вокруг оси y, что соответствует следующим формулам
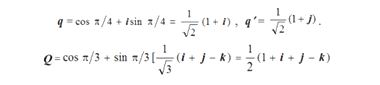
Известны две других формулы задания вращения в трехмерном пространстве: либо через направляющие косинусы:
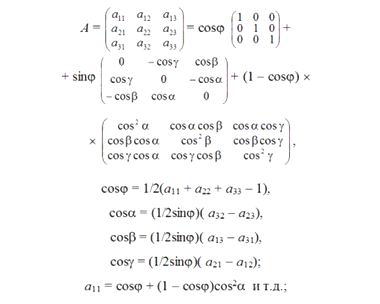
либо через углы Эйлера
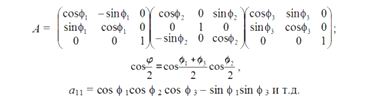
Таким образом, ортогональные повороты в трехмерном пространстве можно описывать тремя способами: непосредственно через кватернион, через 3 х 3 матрицы с направляющими косинусами и через 3 х 3 матрицы с углами Эйлера. Однако никто пока не вывел аналогичные формулы для четырехмерного пространства.
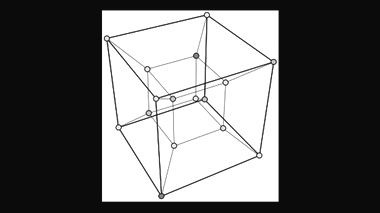
Почему? Да потому что их не существует в математической природе. Релятивисты могут сколько угодно говорить о многомерных пространствах, но математики-конструктивисты знают, что их предмет исследования не произволен. Его нельзя строить по свободной экстраполяции, когда расширение пространства действия определяется простым увеличением пространственных осей (см. К вопросу о размерности).
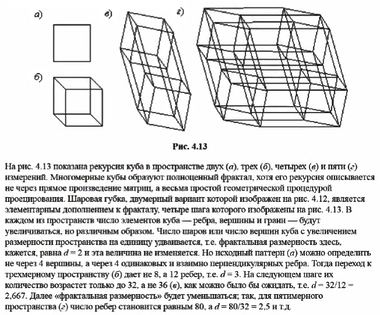
Мы не вправе по своему желанию выдумывать геометрические пространства любой размерности. Это связано с алгеброй групп. Существует геометрия на плоскости: ей ставится в соответствие алгебра комплексных чисел; существует геометрия в пространстве трех измерений: ей отвечает алгебра кватернионов. Но алгебраической структуры, отвечающей четырехмерное пространство, уже не существует.

В самом деле, удвоение кватерниона порождает октаву
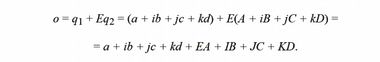
но множество октав уже не образует группы, так как умножение базисных единиц, представленное таблицей 2.50

не является ассоциативным
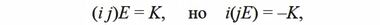
Напомним, алгебраической группой называется замкнутое множество, в котором есть единичный элемент, обратные элементы для всех прямых и выполняется закон ассоциативности, который на множестве октав как раз и нарушается (см. Определение группы и примеры групп).
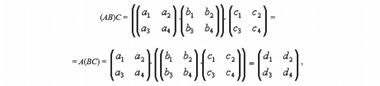
Дальнейшая экстраполяция — удвоение октавы и т.д. — тоже не приводит к числовым агрегатам, имеющим групповые свойства. Следовательно, многомерные пространства — пяти, шести и т.д. измерений — тоже существовать не могут, как и пространство четырех измерений. Есть множества, в которых закон ассоциативности выполняется, они, однако, не образуют группы. Так, в квантовой физике часто приходится иметь дело с матрицами Паули, которые в математике называются спинорами
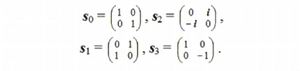
Существует простая связь между спинорами и матрицами базисных единиц кватерниона
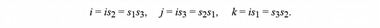
Закон ассоциативности для матриц Паули выполняется в силу общей природы матриц
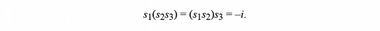
Но группы из них не получается, поскольку множество открыто, а группа должна быть замкнутой на себя. Тем не менее, на них можно построить полезную для физики математическую структуру — алгебру Клиффорда. На матрицах Паули она представляет собой следующий числовой агрегат
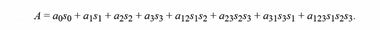
В состав агрегата A входит один скаляр, три вектора, три бивектора и один тривектор (или псевдоскаляр). При перемножении таких агрегатов будут возникать два типа умножения базисных единиц — внутреннее (или скалярное) и внешнее (или векторное).

Примерами внутреннего и внешнего произведений являются дивергенция и ротор, соответственно
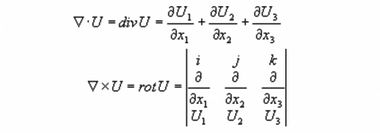
Продемонстрируем силу алгебры Клиффорда на примере электродинамики.
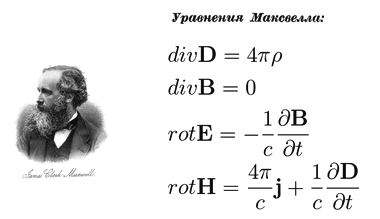
В ней вектор напряженности электрического поля (E) определяется через градиент скалярного потенциала (φ)
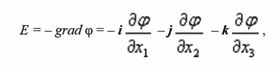
а бивектор напряженности магнитного поля (H) определяется как ротор векторного потенциала (a):
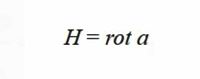
Тогда через клиффордово произведение можно дать все четыре уравнения Максвелла для статического электромагнитного поля:
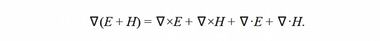
Приведем расшифровку четырех слагаемых
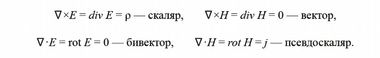
Для динамического случая изменение магнитного поля приводит к возникновению ротора электрического поля, а изменение электрического поля — ротора магнитного поля.
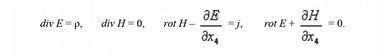
Эти же уравнения, расписанные по четырем составляющим, выглядят следующим образом
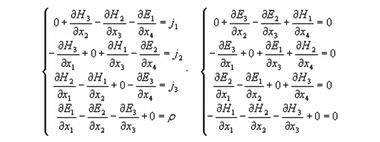
Эти две системы уравнений можно представить в матричной форме
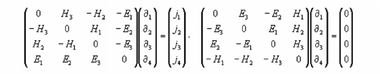
Здесь принято
∂i = ∂/∂xi, ct = x4 и j = ρv или
(j1, j2, j3, j4) = ρ(∂x1/∂x4, ∂x2/∂x4, ∂x3/∂x4, ∂x4/∂x4)Для получения полной симметрии в матрицы и, следовательно, в уравнения Максвелла нужно ввести мнимость, как показано здесь.
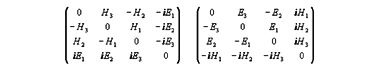
Представленный здесь формализм, кажется, имеет дело с четырехмерным пространством. Но это только кажется. Необходимо помнить, что уравнения Максвелла, описанные при помощи кватернионов, касаются трехмерного пространства. Теперь от электромагнетизма перейдем к механике.
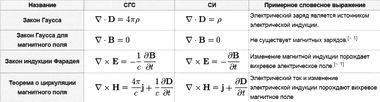
Так выглядит формула кинетической энергии в классической механике
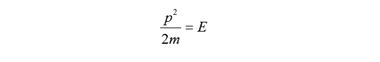
Если имеем дело с электроном, то m – его масса, p –импульс и E –энергия. В квантовой механике энергия и импульс заменяются операторами
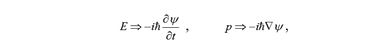
здесь ħ = h/2π – постоянная Планка, i – мнимая единица, ψ – волновая функция электрона, а набла
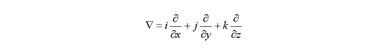
– оператор, с помощью которого удобно выражать операции в векторной алгебре. Мы ими уже пользовались, но не лишним будет напомнить их определение.
Если вектор ∇ скалярно умножить на функцию ψ, то получим вектор
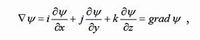
который называется градиентом функции ψ.
Если вектор ∇ скалярно умножить на вектор a, то получим скаляр
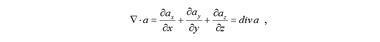
который называется дивергенцией вектора a.
Если вектор ∇ векторно умножить на вектор a, то получим вектор
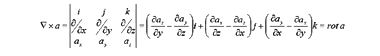
который называется ротором вектора a.
Скаляное произведение оператора набла на оператор набла дает скалярный оператор Лапласа
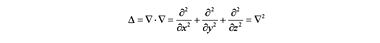
Теперь вернемся к механике. Если выражение для кинетической энергии записать в операторном виде, то получим уравнение Шредингера
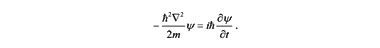
Если вместо классического выражения для кинетической энергии воспользоваться релятивистской формулой
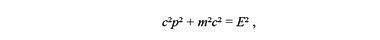
и произвести в ней соответствующую замену на операторы, то мы получим уравнение Клейна — Гордона, описывающее частицы без спина
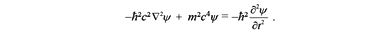
Понизив степень уравнения Клейна — Гордона на порядок, получаем уравнение Дирека для электрона, имеющего спин 1/2
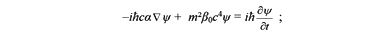
здесь α – 4 на 4 матрицы, составленные из матриц Паули
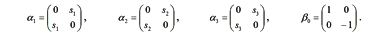
Из трех α-матриц и одной β0 конструируют четыре γ-матрицы, которые называются матрицами Дирака
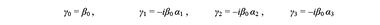
На базе γ-матриц можно простроить 16 компонентную алгебру Клиффорда вида
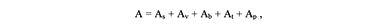
здесь As – скаляр, Av – вектор, Ab – бивектор, At – тривектор, Ap – псевдоскаляр. Базисом этой алгебры выглядит следующим образом
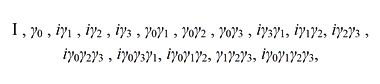
где I – единичная 4 на 4 матрица, i – мнимость. Запишем уравнение Дирака через γ-матрицы. С этой целью уравнение Дирака, записанное через три α-матрицы и одну β0-матрицу умножим на множитель iħβ0, получим уравнение следующего вида
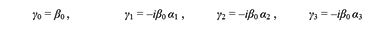
Если воспользоваться оператором 4-импульса, то уравнение Дирака предстанет в более компактной форме
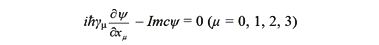
Его решением является плоская волна вида
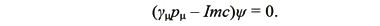
Таким образом, уравнение Дирака представляет собой волновое уравнение. К нему Дирак пришел естественным путем, когда захотел уравнение Шредингера сделать инвариантным для преобразований Лоренца. Ведь можно идти обратным путем, т.е. оттолкнуться от выражения для плоской волны, которая в наиболее общей форме выглядит как
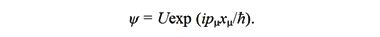
Если функцию ψ один раз продифференцировать по времени
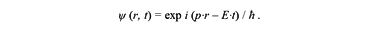
и дважды по координатам
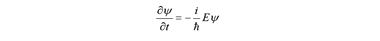
а затем два последних выражения приравнять по Eψ , помня, что
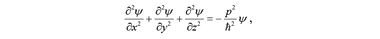
то в результате получаем уравнение Шредингера
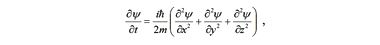
которое удобно записать через оператор набла в квадрате

Среди решений этого уравнения имеются такие, которые зависят только от времени
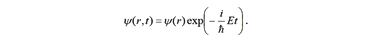
Подставляя это решение в уравнение Шредингера, находим стационарное уравнение для свободного электрона
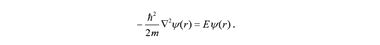
При наличии независимого от времени потенциального поля V(r) последнее уравнение приобретет вид
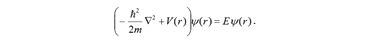
Если вместо кинетической энергии одного-единственного электрона, находящегося в потенциальном электрическом поле, имеется множество электронов, взаимодействующих друг с другом и с остовом кристаллической решетки, то скобка с двумя слагаемыми заменяется гамильтонианом (H). Уравнение Шредингера приобретает вид
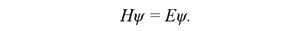
В качестве гамильтониана H при числовом расчете электронных энергетических уровней в кристаллических полупроводниках чаще всего выступает матрица, которая учитывает все энергетические взаимодействия в кристаллической решетке.
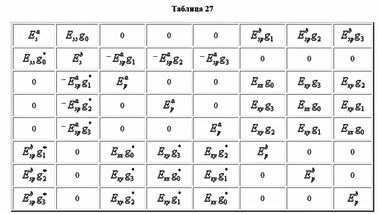
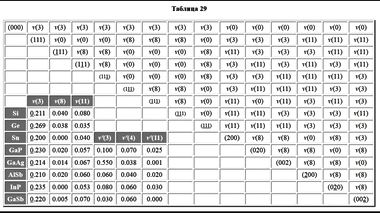
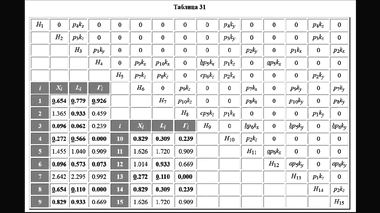
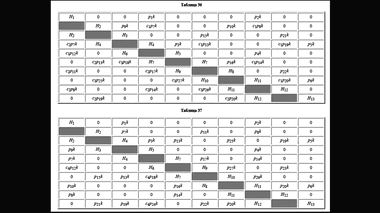
Физика твердого тела начинается тогда, когда теоретик начинает размышлять, как ему сконструировать гамильтониан. Прежде чем погрузиться в толстые слои конденсированного вещества, давайте оглянемся назад и осмотримся по сторонам. Из наших экскурсов в историю физики мы уже знаем, что жизнь науки ничем особенным не отличается от жизни общества. Бывают периоды, когда общество забывает предшествующие события и все достижения текущего момента и готово приписывать какому-нибудь кумиру, который правдами и неправдами оказался на вершине социальной пирамиды. Так было, например, со Сталиным, которому целиком приписали победу во Второй мировой войне, забывая о проявленном героизме бесчисленных анонимов, воевавших на полях сражения. Так было с Ньютоном, который не открывал три закона, носящих сейчас его имя, и закон всемирного тяготения открытый Робертом Гуком.

Релятивисты восхищаются красивой аналогией кривизны пространства, которую якобы впервые предложил Эйнштейн. Но если бы они лучше знали историю физики, то должны были бы упомянуть имя всё того же Гука. В диалогах с Ньютоном, которые в большинстве случаев проходили заочно, Гук для разъяснения эллиптических орбит планет приводил пример не только коническую поверхность, по внутренней поверхности которой катилась планетные тела, но и конический маятник, описывающий эллипсы. По отклонению оси маятника и по измененному периоду колебания он пытался установить степень несферичности Земли.
Сегодня только и говорят о бозоне Хиггса, что можно подумать, будто Питер Хиггс придумал что-то такое, чего до него никто не знал. В действительности, Хиггс высказал старую идею Джозефа-Джона Томсона, которую сначала у этого физика похитил "скромный" Эйнштейн, а позже, придав идее новое словесное обличие, преподнес забывчивой общественности уже в третий раз "первооткрыватель" Хиггс.

В чем заключается идея Томсона?
Еще в 1881 году 25-летний Томсон ввел понятие "связанной с эфиром массы". Движущееся сквозь эфир тело, рассуждал он, должно испытывать сопротивление эфирной среды, которое равносильно увеличению массы тела. Со временем эта мысль приобретала у него более конкретные очертания, особенно, после открытия им в 1897 году электрона (см. Биография Дж. Дж. Томсона. Электрон: история открытия и первые теории).

Сейчас мы покажем несколько любопытных страниц из книги Томсона, написанной по следам прочитанных им лекций в мае 1903 года, т.е. за два года, когда Эйнштейн опубликовал первую работу по теории относительности, и спустя много лет после, зарождения его теории "связанной с эфиром массы". "Нажмите на паузу и прочтите!" (см. Материя и эфир).

Исследуя отклонение катодных лучей в магнитном и электрическом полях, Томсон обнаружил, что лучи представляют собой поток отрицательно заряженных частиц. Проводя бесчисленное количество опытов над ними, измеряя отношение заряда электрона к его массе, он показал, что открытые им частицы почти в 2000 раз легче самого легкого элемента — атома водорода. Самое же главное открытие, которое у него без зазрения совести украли релятивисты, заключается в идее, высказанной им еще в молодости, а именно: масса электронов или β-частиц, из которых состоят катодные лучи, будет расти с увеличением скорости.
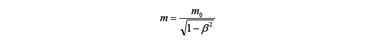
Согласно Томсону, связанная масса электронов в электрическом поле равна кинетической энергии
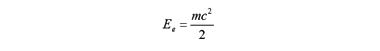
Но ровно такую же энергию электрон приобретет, двигаясь в магнитном поле
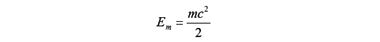
Следовательно, в электромагнитном поле двойка, стоящая в знаменателе формул, исчезнет, поскольку полная энергия движения электрона складывается из этих двух равных друг другу (Ee = Em) энергий
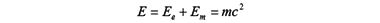
Для Эйнштейна эфир не существовал.

Поэтому увеличение массы электрона во время его движения сквозь пустоту он объяснял кинематическим эффектом, полученным за счет спекулятивных преобразований Лоренца. При этом он извратил идею Томсона, полагая, что энергия электрона сосредоточена в его массе.

Хиггс вернулся к первоначальной идее Томсона путем введения особого поля, которое сегодня называют его именем. Для автора тоже, как будто бы не существовал материальный эфир, но за счет достаточно искусственного деления частиц на фермионы и бозоны он вместе со всеми современными мифотворцами стал говорить о виртуальном пространстве, в котором, дескать, и существует поле Хиггса.
Это эфемерное поле сообщает всем движущимся через него частицам реальную массу. Однако толкователи-популяризаторы заумных фантазий нынешних оракулов от науки по-прежнему оперируются образами, которые в конце 19-го века возникли в голове Томсона.

Они сравнивают частицу с лыжником-слаломистом, стремительно съезжающим с горного склона. Лыже отбрасывают в стороны массу снега, снег оказывает сопротивление движению, стало быть, дополнительную массу лыжника за счет его взаимодействия со снежным покровом можно считать вновь приобретенной.
Почему мы вспомнили об этих исторических фактах? Дело в том, что вскоре после смерти Томсона его прозорливая идея о переменной связанной с эфиром массе перекочевала в физику твердого тала. Тут она неизбежно претерпела некоторые изменения, которые, однако, ничуть не изменили ее суть. Физики-твердотельщики тоже не говорили об эфире, но электроны могут двигаться сквозь электрически заряженную решетку. Таким образом, при своем движении через кристаллическое поля они испытывают периодическое воздействие со стороны остова. Это внешнее воздействие со стороны решетки переносят на массу электронов (или дырок, если иметь в виду полупроводники), которую в этом случае называют "эффективной массой" (см. Эффективная масса и поверхность Ферми).
Двигаясь по различным направлениям внутри кристалла, носители положительного и отрицательного электричества будут испытывать различное воздействие со стороны периодического поля. Поэтому эффективная масса носителей выражается тензором.
Как ее можно определить? Ответ: с помощью так называемых зонных структур.
Они представляют собой множество энергетических уровней для возбужденных электронов. Зонные структуры определяют законы дисперсии, т.е. законы рассеяния электронов на кристаллических решетках, если говорить об алмазоподобных полупроводниках.
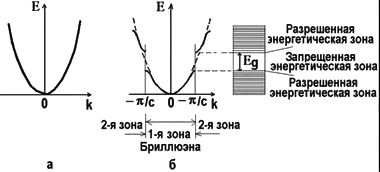
Кинетическая энергия электрона E зависит от волнового вектора k, что называется законом дисперсии E(k). По квадратичному закону найдем первую и вторую производную функции E(k):
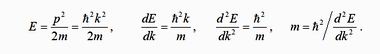
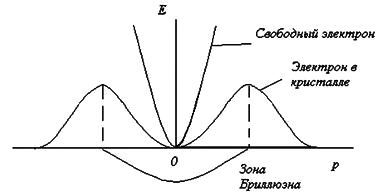
Вспоминаем, что первая производная от какой-либо функции означает скорость изменения функции, вторая производная — степень кривизны функции. Таким образом, масса свободного электрона обратно пропорциональна кривизне функции E(k).

Так как уравнение E(k) представляет собой сферу, поверхность которой имеет постоянную кривизну, то электрон будет иметь неизменную массу, куда бы он ни полетел. Но в кристалле закон дисперсии намного сложнее. Изоэнергетические поверхности отличаются от сферических и, следовательно, масса электрона зависит от направления его движения в k-пространстве:
если d²E/dk² > 0, то m > 0; если d²E/dk² < 0, то m < 0.
Отрицательной массой обладают дырки, положительной — электроны. При смене знака вторая производная закона дисперсии должна быть равна нулю: d²E/dk² = 0, что соответствует бесконечно большому значению массы электрона или дырки. Никакая сила не способна перенести частицы с массой m = ± ∞ из одной точки k-пространстве в другую.
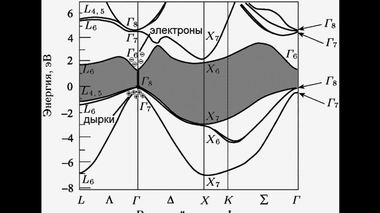
Отсюда следует, что эффективная масса имеет физическое значение вблизи дна зоны проводимости для электронов и вблизи потолка валентной зоны для дырок. Между этими уровнями лежит запрещенная зона. Закон дисперсии вблизи экстремальной точки k0 n-го энергетического уровня запишется как
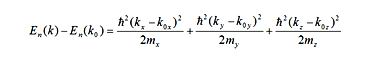
Часто два из трех компонентов эффективной массы одинаковые, и тогда говорят о продольной и поперечной массе.

Физический смысл эффективной массы состоит в том, что направление ускорения электрона (dv/dt) под действием кристаллического поля V(r) не совпадает с направлением силы (F). Если в изотропном пространстве движение электрона описывается вторым законом Ньютона:
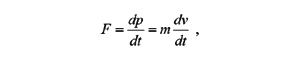
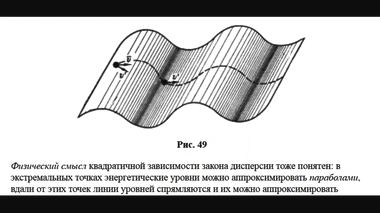
то в анизотропном пространстве кристалла масса в этом школьном законе зависит уже от направления движения (рис. 49). Таким образом, ускорение электрона будет не совпадать с направлением силы:
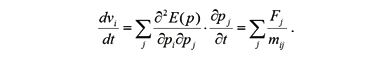
Физический смысл квадратичной зависимости закона дисперсии тоже понятен: в экстремальных точках энергетические уровни можно аппроксимировать параболами, вдали от этих точек линии уровней спрямляются и их можно аппроксимировать прямыми или, если речь идет о k-пространстве, то плоскостями (см. Линейная аппроксимация закона дисперсии).
При поиске параметров импульса возникает потребность опереться на какую-то ориентировочную модель всех энергетических уровней. Эту модель не может дать зонная структура пустой решетки (рис. 44а), поскольку вблизи запрещенной зоны кристаллический потенциал слишком сильно искривляет общую картину энергетических состояний (см. рис. 44б). Значит, требуется более адекватная пространственная модель уровней, дающая наглядное представление о расположении энергетических зон.
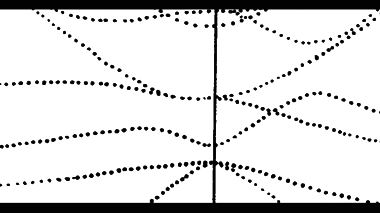
Такая модель может быть получена за счет линейной аппроксимации закона дисперсии, когда ее квадратичный компонент опускается, а линейный удерживается (см. Линейная аппроксимация закона дисперсии):
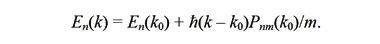
Линейный закон описывает положение плоскостей в четырехмерном пространстве энергии и волнового вектора (E, kx, ky, kz). Таким образом, ставится задача получения числовых значений коэффициентов уравнений плоскости для энергетических уровней, например, германия и кремния. Прежде чем переходить к рассмотрению конкретных законов дисперсии нужно иметь в виду, что существует несколько способов построения гамильтонианов. Среди них выделяется два принципиально различных модели: модель слабой связи и модель сильной связи.
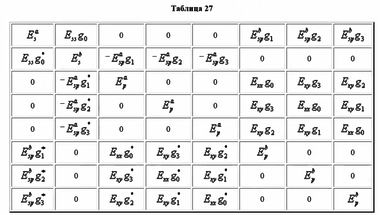
К Модели сильной связи относится так называемый ЛКАО-гамильтониан (ЛКАО расшифровывается как линейная комбинация атомных орбиталей). В этой модели все электроны оказываются связанными с ядрами своих атомов, и только сближение этих атомов внутри кристалла приводит к перекрытию волновых функций электронов, что влечет за собой перестройку орбиталей. Чем ближе атомы в кристалле, тем интенсивнее взаимодействие между электронами, а значит, тем больше значения интегралов перекрытия атомных орбиталей, которые выступают в качестве матричных элементов в матрице ЛКАО-гамильтониана.
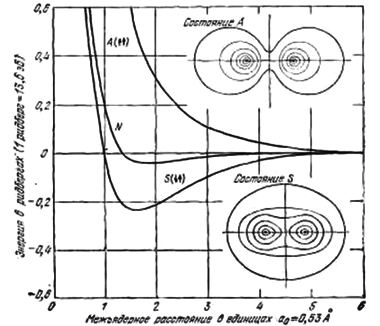
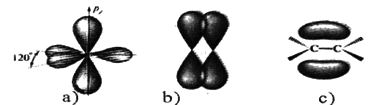
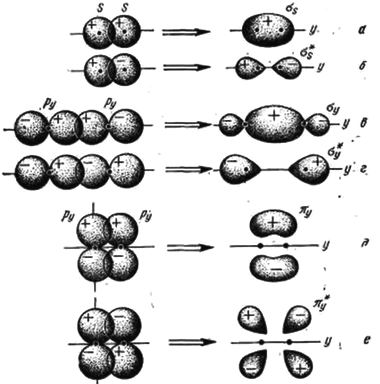
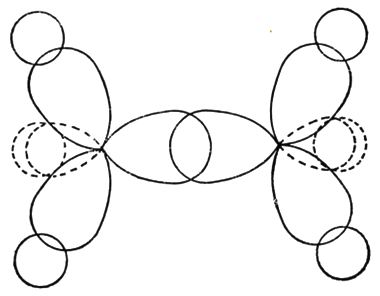
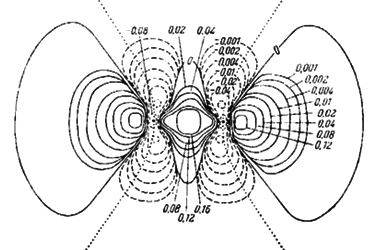
В Модели слабой связи электроны перемещаются внутри кристалла почти свободно. В нулевом приближении потенциал узлов решетки принимается за ноль, электрон абсолютно свободно перемещается внутри остова. Его движение описывается квадратичным законом дисперсии, справедливым для пустого пространства. При потенциале, отличном от нуля, электрон теряет часть свободы перемещения, закон дисперсии становится отличным от квадратичного, но зависимость движения электрона от потенциала решетки выражается все же намного слабее, чем в модели сильной связи.
Для конструирования гамильтонианов по модели сильной и слабой связи нужно тщательно разобраться в подразделах Закон дисперсии по методу ЛКАО и Закон дисперсии в рамках kp-модели, соответственно.Несмотря на различие двух моделей описание симметрии энергетических уровней, с точки зрения теории групп, в них одинаковое. В модели сильной связи оперируют понятиями атомных и молекулярных орбиталей; в модели слабой связи свободно парящие электроны описываются Г-состояниями кристаллической решетки (рис. 42).
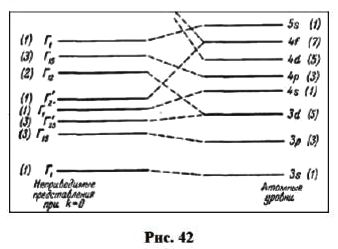
В модели сильной связи считается, что симметрия электронных уровней в кристалле определяется симметрией электронных уровней отдельных атомов, при этом умалчивается, чем, собственно, определяется симметрия уровней отдельно взятого атома. В модели слабой связи, наоборот, говорится, что симметрия электронных уровней вблизи отдельных узлов кристаллической решетки определяется симметрией всей решетки, при этом умалчивается, почему, собственно, кристаллическая решетка приобрела именно такую, а не иную симметрию. В обоих подходах отсутствует ответ об источнике симметрии для свободного атома (в модели сильной связи) и для кристаллической решетки (в модели слабой связи).
Очевидно, что источником симметрии в обоих случаях является эфир, который удобно смоделировать в виде абсолютно твердой кристаллического тела, внутри которой возникают энергетические возбуждения либо в форме свободных атомов водорода, гелия и т.д., либо связанных кристаллических решеток германия, кремния и т.д.
Известные нам кристаллы кремния, германия, арсенида галлия и т.д. образуют вторичную решетку, симметрия которой продиктована состоянием первичной решетки эфира. Но вторичная решетка при определенных условиях температуры, давления и других параметров может служить основой для возникновения производных состояний в виде экситонного газа или электронно-дырочной жидкости, которые являются сверхвеществом внутри обычного вещества.
Пара электрон-дырка описывается с помощью обычного уравнения Шредингера на языке водородоподобных состояний. Различие касается только количественной стороны дела. Так, величина радиуса Бора, энергия связи и прочие характеристики для электрона и дырки будут на порядок или два различаться по сравнению с аналогичными характеристиками в кристаллическом германии или другом полупроводнике, где экситон возникает. Для экситона кристаллическая решетка выступает в роли эффективного вакуума, т.е. нейтрального фона, который находится совершенно в другом энергетическом диапазоне, чем электроны и дырки в кристалле того же германия.
Перед тем как переходить к законам дисперсии, напомним, что понимается под k-пространством.
Если узлы прямой решетки определить равенством
Ri = n1a1 + n2a2 + n3a3,
то узлы обратной решетки определятся другим равенством
Ki = m1b1 + m2b2 + m3b3,
причем базисные векторы обоих пространств ортогональны и нормированы.

На рис. 32 показано 14 пространственных ячеек Браве.
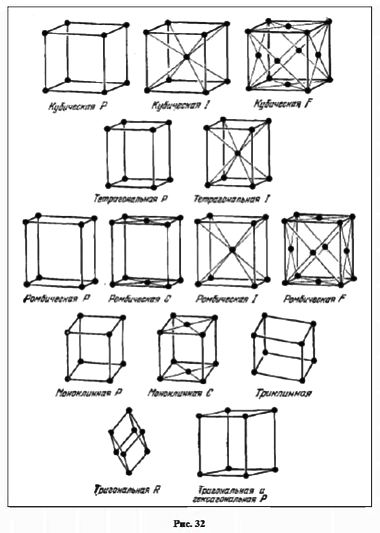
Для каждой из 14 элементарных ячеек можно построить элементарные ячейки обратной решетки.
Важно уметь построить одну-единственную элементарную ячейку, поскольку закон дисперсии En(k) приводится только для нее одной, и здесь на первый план выдвигается понятие зоны Бриллюэна (ЗБ). Первую ЗБ определяют как область в обратном пространстве, окружающую один из узлов обратной решетки и ограниченную набором плоскостей, проходящих через середины векторов, соединяющих в обратной решетке данную точку с ее ближайшими соседями.
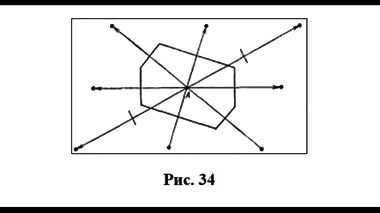
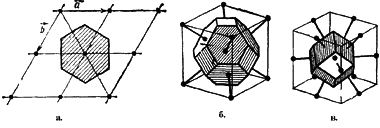

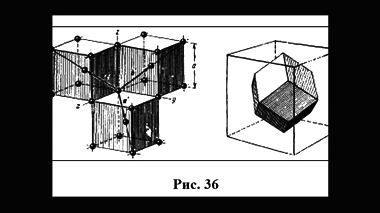
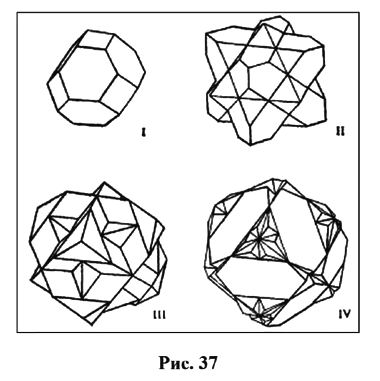
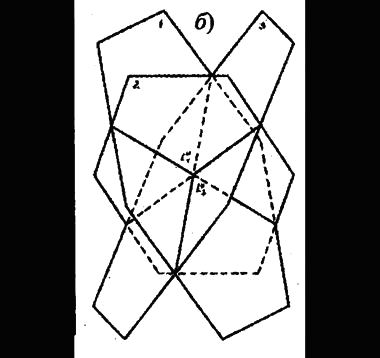
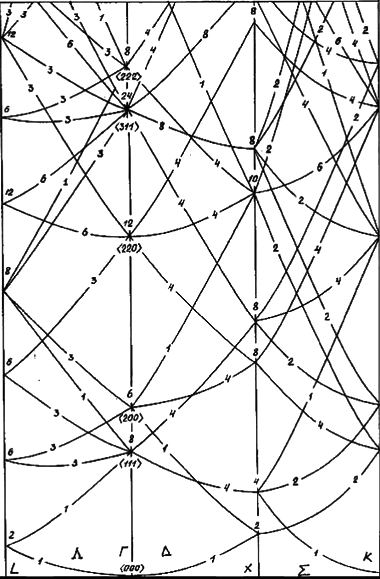
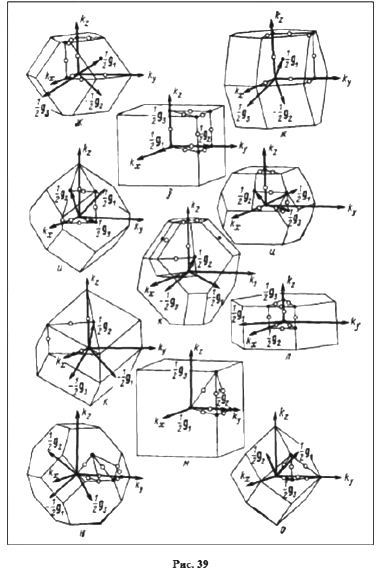
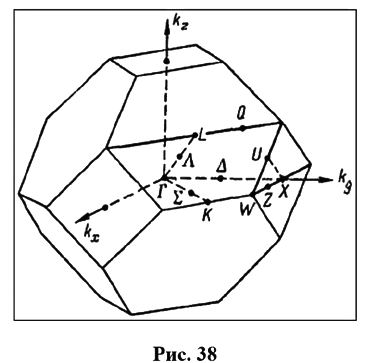
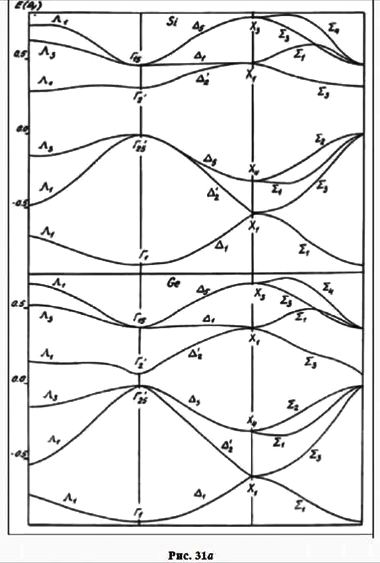
На рис. 34 показана первая ЗБ для двумерной косоугольной решетки; на рис. 35 вычерчены уже десять ЗБ для двумерной квадратной решетки. Точно таким же половинным делением расстояния между двумя узлами определяется ЗБ в трехмерном пространстве. На рис. 36а приведены базисные векторы ОЦК решетки, а на рис. 36б — первая ЗБ, имеющая форму правильного ромбододекаэдра. На рис. 37 приведены первых четыре ЗБ для ГЦК решетки. На рис. 38 указаны симметричные точки (Г, L, Λ, Δ, …) первой ЗБ для ГЦК решетки, представляющей собой полуправильный многогранник Архимеда — усеченный октаэдр. Симметричные точки и направления можно видеть на энергетических зонах, рассчитанных ЛКАО-методом (рис. 31а).
Итак, законы дисперсии (их еще именуют зонными структурами), полученные при помощи гамильтонианов, построенных на основе модели сильной связи, можно аппроксимировать кусками параболы. Законы дисперсии, полученные при помощи гамильтонианов, построенных на основе модели слабой связи, можно аппроксимировать отрезками прямых.
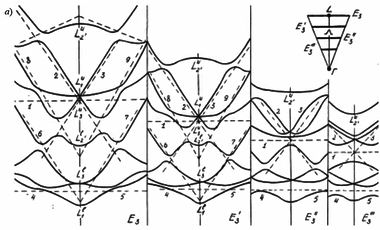
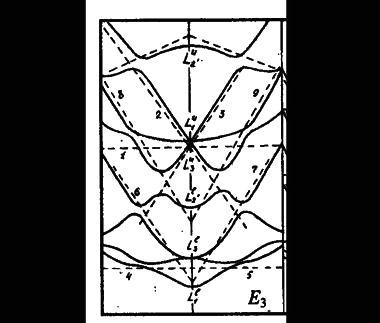
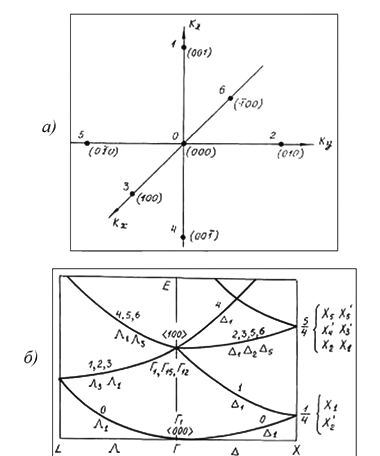
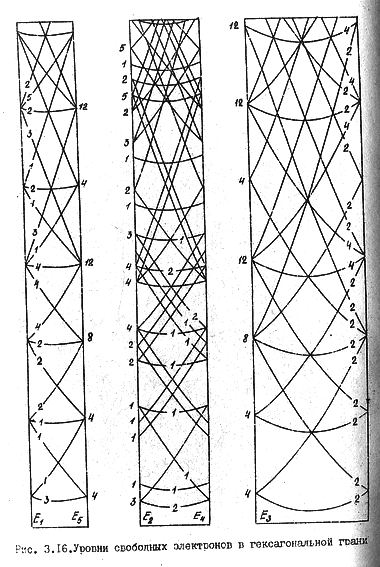
Чтобы продемонстрировать роль линейных элементов зонной структуры, обратимся к восьми нижним состояниям зоны проводимости германия на гексагональной грани зоны Брюллюэна (рис. 59). Расчет зоны производился по модели слабой связи электронов с помощью матрицы гамильтониана Г(15 × 15).

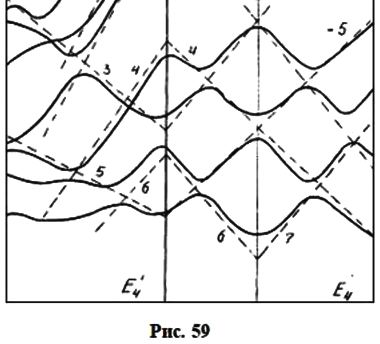
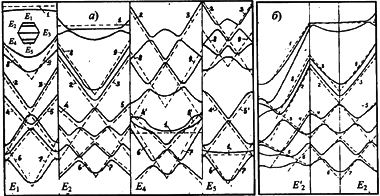
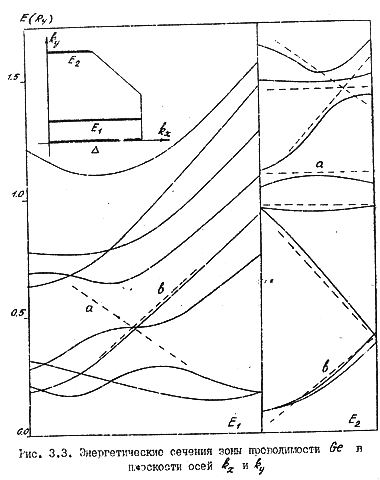
Здесь пунктирными прямыми обозначены следы от энергетических плоскостей, которые снабжены цифрами. На рис. 59а показаны четыре сечения Е1, Е2, Е4 и Е5. Два связанных сечения Е2 и E'2, показанные на рис. 59б, даны для того, чтобы можно было проследить связь энергетических уровней на гексагональной грани зоны Брюллюэна с уровнями, расположенными ближе к центру зоны Брюллюэна. Сечение E'2 проведено параллельно оси knz.
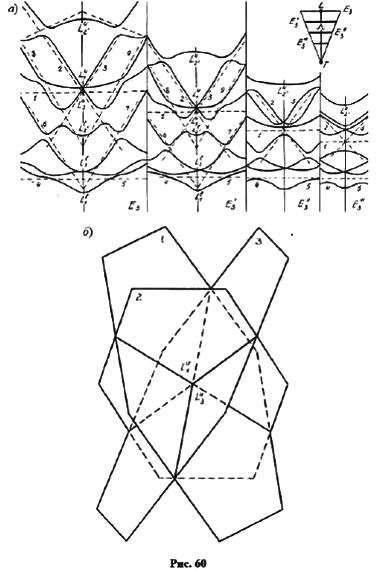

Центральное сечение E3 изображено на следующем рис. 60а вместе с внутренними сечениями E'3, E''3, E'''3, параллельными линии E3 и проведенными в глубине зоны Брюллюэна. Общего числа сечений, представленных на рис. 59 и 60 достаточно, чтобы восстановить линейную конфигурацию восьми нижних состояний зоны проводимости германия. На рис. 60б показано пространственное расположение первых трех из восьми плоскостей.
Следующий шаг состоит в том, чтобы записать уравнения плоскостей в удобной системе координат. Первая система координат вводится на гексагональной грани ЗБ с осями Е, k'x, k'y. По формулам аналитической геометрии записывается в трехмерном пространстве. Однако сечения E'3, E''3, E'''3 дают зоны дисперсии в глубине ЗБ и, тем самым, вводят еще одно измерение.
Три плоскости, обозначенные 1, 2 и 3, по выбранным соответствующим образом точкам можно записать в пространстве четырех измерений Е, kx, ky, kz. Тогда при наличии оси симметрии третьего порядка три уравнения плоскости переходят одно в другое при циклической перестановке координат волнового вектора kx, ky, kz, так что достаточно выразить линейным уравнением лишь одну какую-то плоскость. Но здесь-то как раз и возникает основная проблема, о которой мы постоянно твердили: четырехмерное пространство не существует.
Многие знают, как записать уравнение плоскости, проходящей по трем точкам, например, таким:
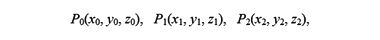
тогда уравнение плоскости получится приравниванием нулю определителя размером 3 на 3:
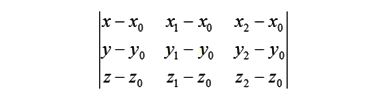
Пусть этими точками будут:
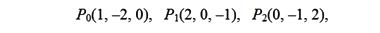
тогда определитель будет выглядеть так
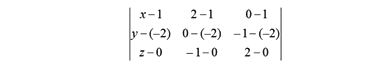
Разложим этот 3 на 3 определитель по первому столбцу на три определителя 2 на 2; в итоге получаем следующее уравнение искомой плоскости:
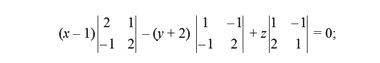
или, окончательно
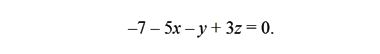
Казалось бы, почему бы нам по аналогии не построить определитель 4 на 4 — вот такого вида
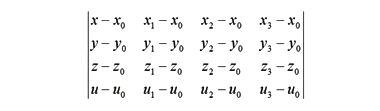
для четырех точек, взятых из конкретного закона дисперсии
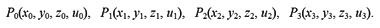
Далее, раскладываем полученный 4 на 4 определитель по первому столбцу на четыре определителя 3 на 3. Потом, повторяем эту процедуру до тех пор, пока не получим уравнение вида
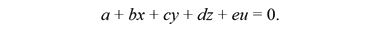
К сожалению, данное расширение формул не работает. Какие бы четыре точки вы не взяли из закона дисперсии, по ним невозможно получить уравнение плоскости в четырехмерном пространстве энергии-импульса. В процессе вычисления коэффициентов a, b, c, d, e возникает линейная зависимость между промежуточными уравнениями, так что окончательного уравнения вы не получите.
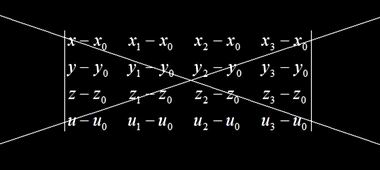
Единственное, что удается здесь получить, это некое псевдоуравнение, например, следующего вида:
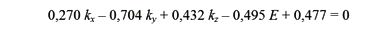
Данное уравнение есть конкретное выражение линейного закона дисперсии En(k) для целой группы состояний, объединенных системой трех плоскостей, но только в разрезе E3, т.е. на гексагональной грани ЗБ. Но оно (уравнение) не дает нужные точки для плоскостей, лежащих в глубине ЗБ, т.е. в разрезах E'3, E''3, E'''3.
Все рассуждения, относительно плоскостей 1, 2, 3, можно перенести на нижние плоскости, которые обозначены цифрами 4, 5, 6, 7, 4', 5'. Уравнение плоскости 6 можно получить из уравнения плоскости 7, поменяв местами переменные ky и kz, а координату kx оставив без изменения. Осуществив, таким образом, перестановку координат, из этих двух уравнений получаем еще четыре. Приведем одно из них:
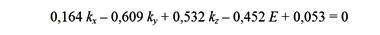
Однако это уравнение тоже описывает энергетические уровни только на гексагональной грани ЗБ E3 и не описывает плоскости в сечениях E'3, E''3, E'''3.
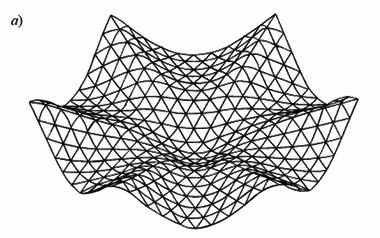
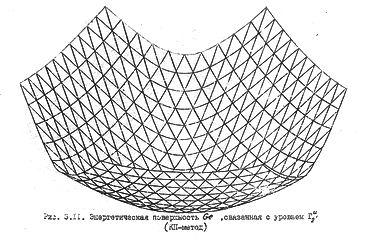
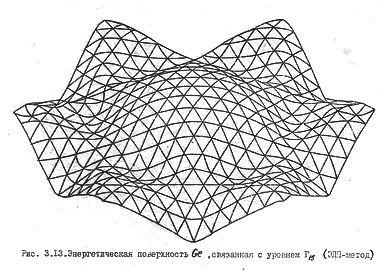
Шесть плоскостей, аппроксимирующих все нижние состояния зоны проводимости, нетрудно вычертить отдельно, как мы это уже делали для плоскостей 1, 2, 3 (рис. 60б). Однако лучшей иллюстрацией взаимного расположения этих плоскостей является графическое изображение точного машинного расчета дна зоны проводимости германия, показанного на рис. 61а. Симметрия этой поверхности для других алмазоподобных полупроводников примерно такая же.
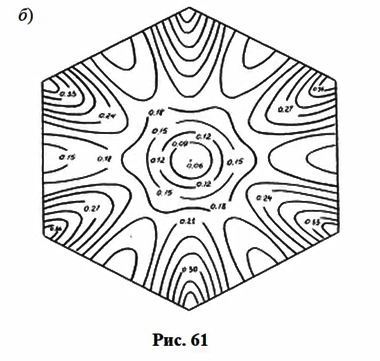
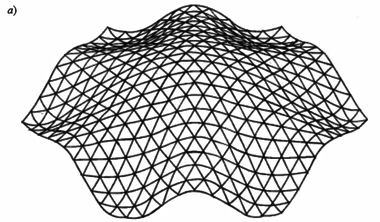
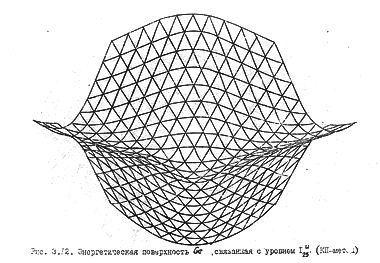
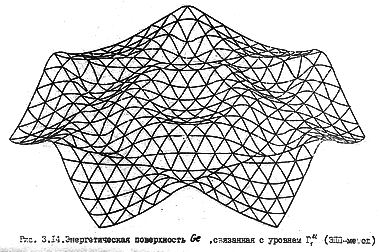
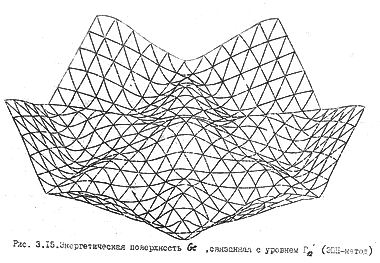
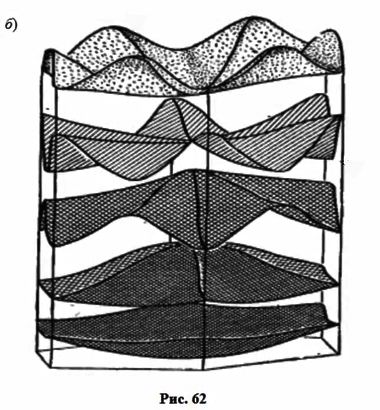
Геодезия дна зоны проводимости германия приведена на рис. 61б. Числами на линиях обозначены уровни энергии в ридбергах, отсчитанные от потолка валентной зоны ( Г '25). В центре розетки находится минимум зоны проводимости. Глубина складок энергетической поверхности потолка валентной зоны меньше, чем у поверхности дна зоны проводимости (рис. 62а). Таким образом, если для дна зоны проводимости мы еще может распознать плоскости, то для потолка валентной зоны они просматриваются с трудом; здесь преобладает квадратичный элемент закона дисперсии.
Потолок валентной зоны германияДругие энергетические уровни.
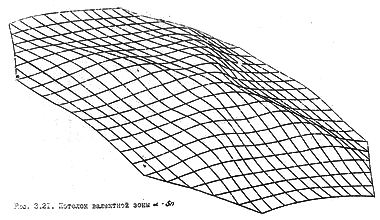
Общая структура энергетических зон в гексагональной плоскости первой ЗБ для полупроводников IV группы изображена на рис. 62б.
Итак, по аналогии можно, конечно, написать выражение для определения расстояния между двумя точками x и y в каком-нибудь n-пространстве:
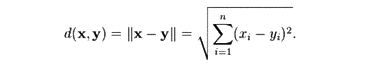
Можно вычертить n-куб или n-сферу в n-мерном пространстве. Можно даже подсчитать у них число вершин и ребер или число параллелей и меридианов. Но какое отношение всё это имеет к реальному миру физики? Ровным счетом — никакого!
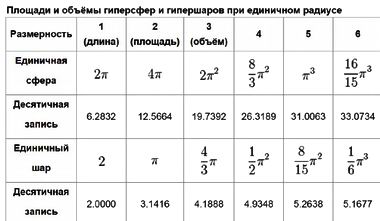
Кажется, что закон дисперсии можно представить в четырехмерном пространстве энергии-импульса, где одна ось отводится под энергию, значение которой выражается действительным (или, вещественным) числом, а три оставшиеся оси с мнимыми ортами i, j, k отводятся под импульс. Некоторые релятивисты в спорах со мной утверждали, что само слово "кватернион" означает четыре. Значит, говорили они, это гиперкомплексное число образует векторное пространство размерности четыре.
Никогда не спорьте с релятивистом; это вредно для вашего здоровья.Верно, что ирландский математик Уильям Гамильтон в 1843 году, находясь на мосту Брум Бридж в Дублине, открыл гиперкомплексное число с четырьмя базисными единицами — одной вещественной и тремя мнимыми. На мосту установлена памятная доска с надписью «Здесь на прогулке, 16 октября 1843 года, во время вспышке гениальности, сэр Уильям Роуэн Гамильтон открыл формулу перемножения базисных единиц кватерниона
Уильям Гамильтон
Памятная доскаИстория открытия кватерниона была долгой и началась она с введения комплексного числа. В течение 17-го века в трудах Лейбница, Муавра, Котса, Эйлера, Даламбера, Гаусса и других математиков это понятие конкретизировалось и успешно применялось в различных областях знаний. В течение длительного времени математики безуспешно пытались построить алгебраический объект с одной вещественной и двумя мнимыми единицами, но у них ничего не получалось. И вот Гамильтон, отказавшись от трехчленного базиса, решил поэкспериментировать с четырьмя базисными единицами.
Его неожиданный успех заставил прочих математиков крепко задуматься: из скольких базисных единиц можно построить полноценное пространство. В 1877 году Георг Фробениус доказал теорему, что гиперкомплексного числа на базе трех единиц построить невозможно. Вторая половина 19-го века — это время интенсивного развития алгебры, в том числе векторной.
Уильям Клиффорд
Лондонский университет
Королевское обществоМаксвелл применил кватернионы для описания законов электродинамики — о чем мы уже знаем. 26-летний Уильям Клиффорд по рекомендации Максвелла был зачислен на кафедру математики и механики Лондонского университета, а в 1874 году он стал членом Королевского общества. Еще через два года он уже докладывал об успехах своей алгебры, о которой мы рассказывали, а также о системе, построенной на бикватернионах. Окончательно аппарат векторной алгебры сформировался в последнем десятилетии 19 века в трудах Гиббса и Хевисайда.
Гиббс
Хевисайд
Работы Минковского, Борна и других релятивистов лежат где-то примерно в той же самой плоскости, что и алгебраистов 19-го века. Они хотели придумать что-то наподобие векторной алгебры для теории относительности, которая замышлялась как физика, существующая в пространстве четырех измерений. Увы, у них ничего не вышло; всё было перепахано вдоль и поперек задолго до них. Первоклассные математики 19-го столетия однозначно показали: кроме кватернионов, нет других алгебраических систем, которые бы можно было применить для реального физического мира. Минковский и Борн создали совершенно не жизнеспособную геометрию, изобилующую грубыми математическими ошибками, о которых мы говорили ранее.
Сегодня по проложенной ими кривой дороже устремились нынешние релятивисты, предложившие пространство 10 измерений. Обреченность таких построений вытекает хотя бы из того печального факта, что в основу своих построений они заложили мертворожденное четырехмерное пространство Минковского.
Сталин, Иосиф Виссарионович, Председатель Совета министров СССР, многолетний лидер Советского государства.
Сталин, Иосиф ВиссарионовичФадеев Александр Александрович, автор романа "Молодая гвардия", генеральный секретарь, а потом и председатель правления Союза писателей СССР, в создании которого, начиная с 1932 года, он принимал активное участие.
Фадеев Александр АлександровичРассказывают, будто Сталин однажды сказал Фадееву: "Нет у меня для вас других пространств, кроме трехмерных".
Сталин шутитШутка.
См. фильм с этим текстом
http://youtu.be/0IzCHjo4j4g